三亚地区电离层foF2的混沌特性分析及其预测研究

朱正平，阮鹏飞

(中南民族大学 电子信息工程学院，武汉 430074)

电离层作为地球空间环境的重要组成部分，其时空变化对无线通信、雷达监测、卫星导航等地空无线电系统产生显著的影响[1-3].当电离层存在扰动或发生电离层暴时，会阻碍无线电的传播，造成通信设备不能正常工作，甚至系统部分功能丧失.因此，需要对电离层状态变化作出及时的监测和预报，以保障无线系统的可靠运行.

电离层F2层临界频率foF2是电离层研究中的一个重要参数，其状态会随着地方时，经、纬度，地磁、太阳活动以及大气活动等多种因素的变化而变化，表现出很强的非线性特性[4,5].研究电离层F2层临界频率foF2的变化特征，对foF2进行一定的预报，有助于加深对电离层的认识，具有重要的意义.针对电离层foF2的预报分为长期预报和短期预报.在长期预测方面，最具影响力的当属国际参考电离层模型(International Reference Ionosphere,IRI).该模型是根据长期的历史数据建立起来的反应电离层变化规律的一些经验公式，描述了电离层的平均特性[6].这导致长期预测方法在实时性预测精度稍显不足.在短期预报方面，文献[7]进行了电离层foF2暴时预报尝试.文献[8]基于支持向量机对电离层foF2进行短期预测.文献[9]建立了基于AdaBoost的电离层foF2参数预报方法，并讨论了预测误差随季节、太阳活动和纬度变化的变化特征.文献[10]将灰色理论应用于电离层foF2的短期预报中，并利用中国地区多个观测站的观测数据进行检验.本文基于混沌理论，利用三亚综合观测站2013年全年观测数据，对电离层foF2的短期预报进行研究，并对其预测精度、误差做出了综合比较和优缺点分析.

1 电离层foF2的混沌特性分析

1.1 时间延迟和嵌入维数的确定

混沌时间序列分析和预测的基础是TAKENS，PACKARD等提出的状态空间重构理论[11，12].Takens定理指出，对于无限长、无噪声的数据序列，时间延迟τ的选取没有限制，嵌入维数m也可以充分地大.实际上，由于数据长度有限且带有噪声，时间延迟τ和嵌入维数m不可能无限大.合适的τ和m对重构的相空间质量尤为重要，进而影响模型的构建和预测.

对于时间序列X={xi|i=1,2,…,N},根据相空间重构理论，可得到如下新的矢量序列：

Y={yi|yi=[xi,xi+τ,…，xi+(m-1)τ]T,
i=1,2,…,M}，

(1)

其中m为嵌入维数，τ为时间延迟，M=N-(m-1)τ为相空间中的相点数.

根据构造的相空间，定义关联函数如下：

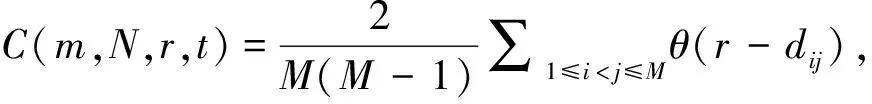
(2)

其中,

dij=‖yi-yj‖∞,

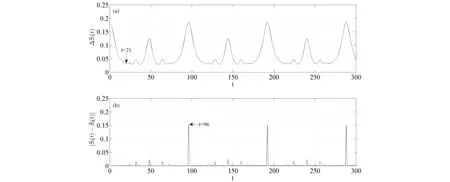
图1 电离层foF2时间序列与的变化曲线Fig.1 Change curve of and for ionosphere foF2 time series

1.2 最大Lyapunov指数判断混沌特性

Lyapunov指数是相空间中相近轨道的平均收敛性或平均发散性的一种度量，它能表征混沌系统中奇怪吸引子的运动性态，是定量判断一个系统是否具有混沌特性的重要指标[14].若时间序列的最大Lyapunov指数大于0，则证明该时间序列具有混沌特性，且Lyapunov指数越大，混沌特性越明显.为了说明电离层foF2存在混沌特性，应用小数据量法[15]计算最大Lyapunov指数，得到其值λ=0.1264，由此可以说明电离层foF2时间序列存在混沌行为.

2 foF2时间序列的混沌预测

混沌时间序列的预测方法包括：全域法、局域法、基于Volterra级数的预测方法和基于神经网络的预测方法等.由于神经网络具有对非线性系统强有力的刻画与建模能力，目前在非线性函数逼近模型中得到广泛应用.本文采用RBF(Radial-Basis Function)神经网络对foF2时间序列进行预测.

2.1 RBF神经网络的结构

RBF神经网络是一种以径向基函数作为隐含层中变换函数的三层前向网络，能模拟人脑中相互覆盖接收域和局部调整的神经网络，已证明它能以任意精度逼近任一连续函数[16]，其拓扑结构如图2所示：

图2 RBF神经网络结构图Fig.2 Structure of RBF neural network

第一层为输入层，其信号源节点的输入个数等于输入向量的维数；第二层为隐含层，径向基函数一般选择高斯函数作为隐含层单元的基构成隐含层空间.隐含层单元数能够影响网络性能，根据实际问题需要而定.第三层为输出层，输出节点对隐含层单元进行线性加权求和，得到输出结果.

2.2 RBF神经网络的映射关系

输入层空间到隐层空间X→R为非线性映射.设网络输入向量X的维数为m，隐含层单元数为q，则RBF神经网络的第i个隐含层单元输出可表示为：

(3)

式中，ci为第i个隐含层单元高斯函数的中心矢量，与输入向量X维数相同，σi为第i个隐含层单元高斯函数的宽度，且大于零，‖·‖为欧式范数.

从隐含层空间到输出层空间R→Y为线性映射.设网络输出向量Y的维数k，则RBF神经网络输出向量Y的第j个输出单元可表示为：

(4)

式中，Ri为第i个隐含单元的输出，wij为第i个隐含层单元与第j个输出层单元的连接权值，q为隐含层单元数.

3 foF2预测结果分析

本文采用了IRI-2016版[17]，样本数据采用了三亚电离层观测站2013年全年foF2观测数据，由于观测设备故障等原因，11月中下旬数据缺失，因而忽略.考虑到季节因素对电离层变化特性的影响，故将观测数据分为春、夏、秋、冬4组分别进行处理，各季节对应月份分别为春(3-4月)、夏(5-8月)、秋(9-10月)、冬(11-2月).

根据前述方法，将每组数据分为训练样本和测试样本两部分.通过训练数据优化网络的各参数性能，从而对后半部分进行预测，并将预测结果与实测结果进行对比分析.

图3为三亚台站2013年foF2参量分季节预测结果对比，图中蓝线代表实测值，黑线代表IRI模型的预测值，红线代表RBF神经网络预测值，绿线代表Volterra模型预测值.从图3中可以看出，国际参考电离层模型对四个季节的预测值与实测值误差相对较大.IRI模型数据曲线较为平滑，各季节foF2每天的变化曲线基本相似，没有完全反映出其变化过程中的细节.相对于foF2上升阶段，IRI模型在foF2下降阶段表现较差，但整体上反映了foF2的变化特点，部分阶段也取得了不错的预测效果.RBF神经网络和Volterra模型对4个季节的预测均保持了较小的误差和较高的精度.foF2在极大值或极小值附近的波动，预测值均能较好的表现出来.对于Es频发的夏季，利用这两种方法也能实现很好的预测.

a)春；b) 夏；c) 秋；d) 冬图3 三亚台站分季节预测结果对比Fig.3 Comparison of seasonal forecast results of Sanya station

为直观地表现电离层foF2预报性能，计算了预报值与实测值的绝对误差ΔfoF2,其公式如下：

ΔfoF2=foF2obs-foF2pred,

(5)

其中foF2obs为某一时刻的观测值，foF2pred为同一时刻模型的预测值.这里将绝对误差>3MHz和<-3MHz的数据点分别归于±3MHz处，且将其作了正态拟合，得到如图4所示的三亚台站foF2绝对误差统计直方图.

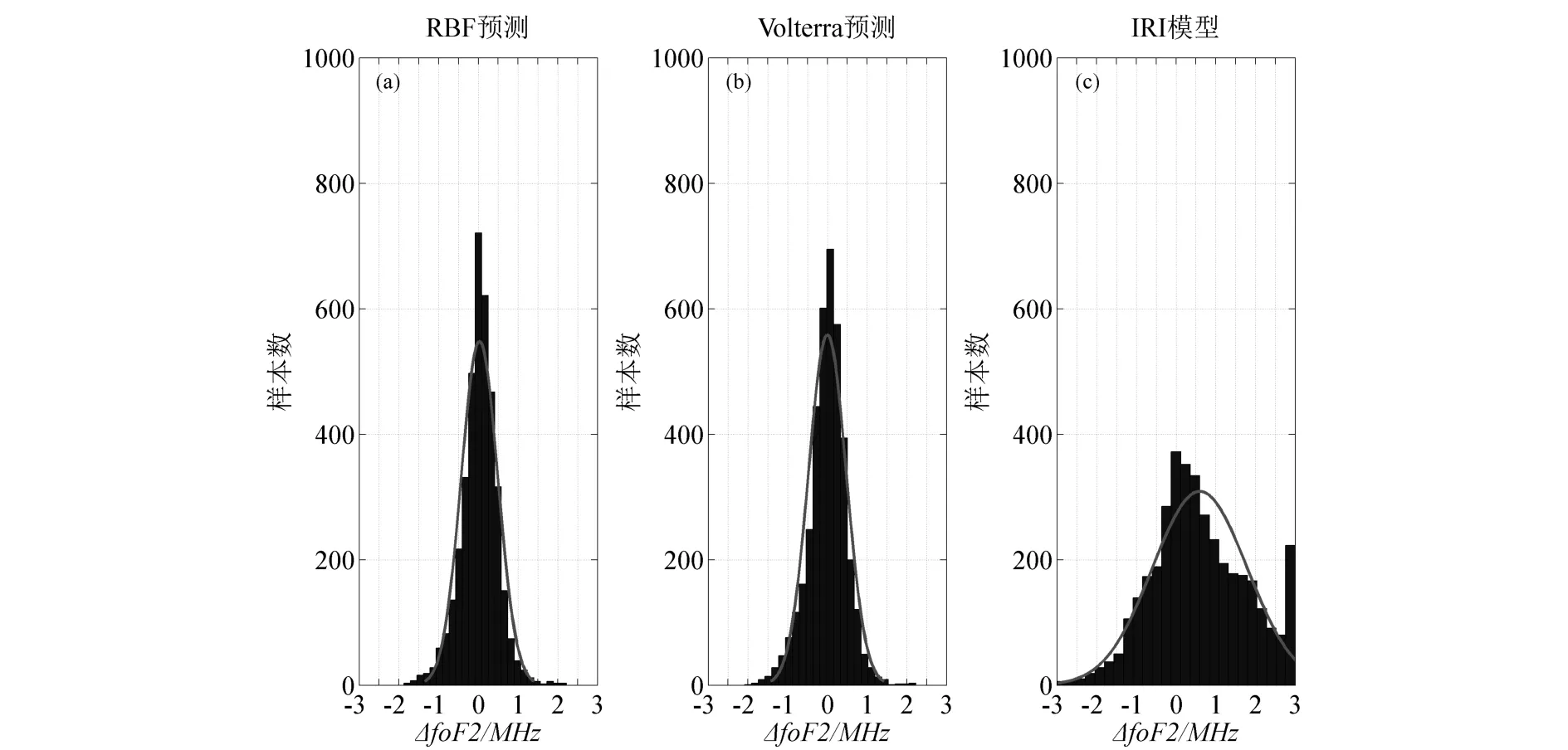
图4 三亚台站ΔfoF2统计直方图Fig.4 Statistics histogram of ΔfoF2 in Sanya station

从图4中可知，RBF神经网络方法和Volterra方法的绝对误差分布的更为集中，误差主要在±1MHz,而IRI模型绝对误差分布较为分散，误差主要在-1.5MHz到+2.5MHz之间.从正态拟合情况可知，图4(a)、(b)中ΔfoF2的均值约为0，正负绝对误差样本数目大致相等，图4(c)中ΔfoF2的均值约为0.5MHz,正误差数目要多于负误差数目，表明IRI模型预测值在多数情况下低于实测值.

为评估预报模型性能的好坏，分别计算foF2的均方根误差(RMSE)和平均相对误差(RE)两个指标，具体定义如下：

(6)

(7)

式中，foF2obs和foF2pred分别为某一时刻的观测值和预测值，N为样本数据总数.

表1 三种方法预报三亚地区foF2结果比较

Tab.1 Comparison of foF2 results in Sanya by three methods

RBFRMSE/MHzRE/%VolterraRMSE/MHzRE/%IRIRMSE/MHzRE/%0.5093.900.5224.041.57811.370.3383.120.3783.491.62313.420.5335.110.5255.081.0277.380.4314.390.4544.501.24010.660.4534.130.4704.281.36710.71

表1给出了三种方法对三亚地区电离层foF2预报的统计结果.从均值上看，RBF神经网络预报的均方根误差和平均相对误差分别为0.453MHz和4.13%，较IRI模型分别提高了0.914MHz和6.58%.Volterra级数模型的均方根误差和平均相对误差分别为0.470MHz和4.28%，较IRI模型分别提高了0.897MHz和6.43%.RBF神经网络预报结果较Volterra级数模型分别提高了0.017MHz和0.15%.RBF神经网络预测性能要稍强于Volterra级数模型，但两者都比IRI模型有较大提高.从中也可看出，预报的均方根误差和平均相对误差随着季节的变化而有所不同.

为研究电离层foF2预测的时间尺度，图5给出RBF神经网络多步预测电离层foF2的结果.从图5中可知，预测值在前三天的误差相对较小，随着时间的推移，预测误差逐渐趋于随机，预测将变得越来越不可信.说明利用RBF神经网络进行预测存在一个时间尺度，超出该预测范围，预测的准确性将会降低，预测将失去意义.

图5 RBF神经网络多步预测电离层foF2Fig.5 Multistep prediction of ionospheric foF2 by RBF neural network

图6为2013年8月16日三亚台站电离层foF2提前N小时预测结果.图中标明了各预测值与实测值间的均方根误差以及相关系数.从图中可看出，随着预测时间的延长，RBF预测结果和实测结果吻合度逐渐下降，局部变化细节变得模糊，趋向于IRI模型预测结果.RBF预测结果的均方根误差(RMSE2～RMSE5)逐渐增大，相关系数(ρ2～ρ5)逐渐减小，这也说明RBF预测值与实测值的相关性会随着预测时间增长而下降.

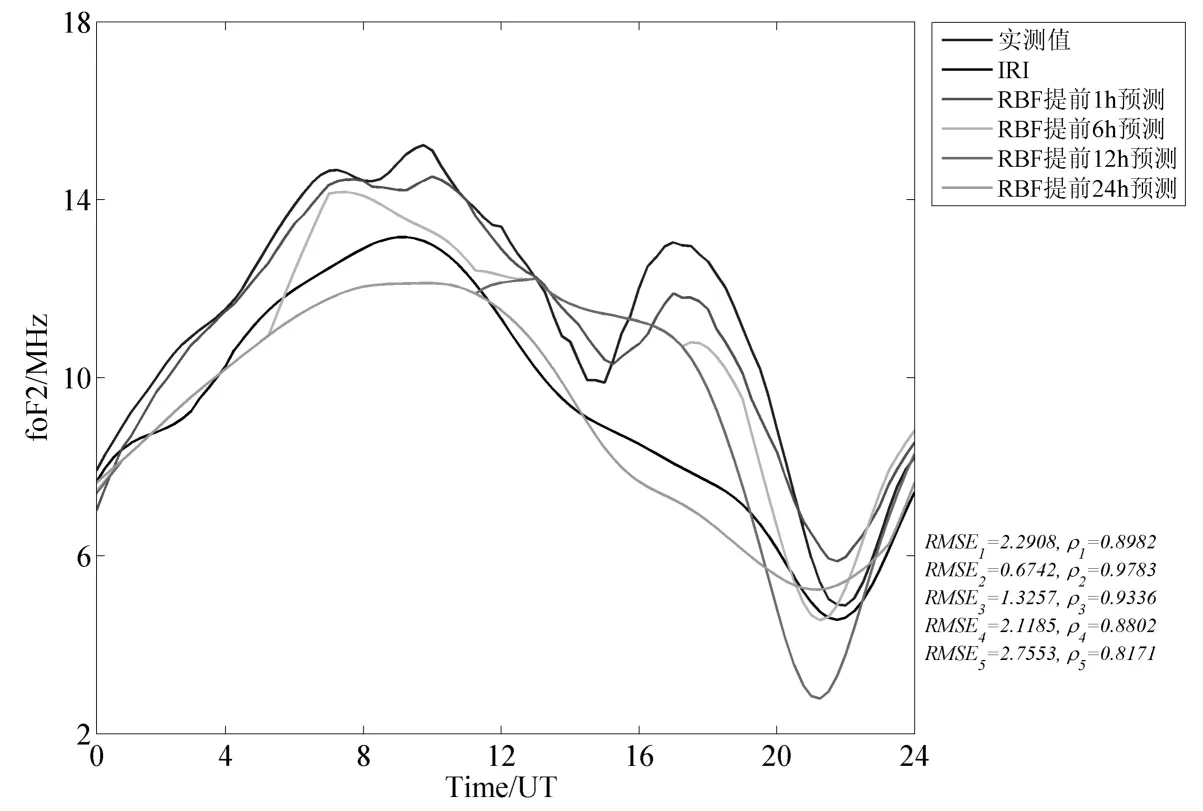
图6 电离层foF2提前N小时预测结果Fig.6 Ionospheric foF2 predicted results N hours in advance

表2为RBF神经网络提前预报三亚地区foF2统计结果，其表现出与图6一致的变化趋势.随着预测时间增加，均方根误差和相对误差逐渐增大，说明预报尺度越小，预报效果越好.RBF在24h内的预报效果要好于IRI模型.

表2 RBF神经网络提前预报三亚地区foF2统计结果Tab.2 Statistical results of foF2 in Sanya predicted by RBF neural network in advance

图7给出了2013年三亚台站在00:00UT和12:00UT时刻预测值和观测值的散点图，其中，图(a)、(b)为RBF结果，图(c)、(d)为IRI结果，图中的红线为拟合的线性回归线.从中可以看出，在00:00UT时刻，RBF模型相关系数为0.8585，IRI模型相关系数为0.6533.12:00UT时，RBF模型相关系数为0.8955，IRI模型相关系数为0.6564.RBF模型预测值和实测值的相关性要明显好于IRI模型，短期预测RBF模型要优于IRI模型.

图7 RBF、IRI在2013年三亚台站foF2预测值与实测值00:00UT(a、c)和12:00UT (b、d)的散点图Fig.7 Scatter plots of predicted and measured values of RBF and IRI at 00:00UT (a, c) and 12:00UT (b, d) of Sanya station foF2 in 2013

4 结语

利用三亚地区2013年电离层F2层临界频率foF2的观测数据，本文开展了对foF2时间序列的混沌特性分析及其预报的研究，结论如下：

(1)对电离层F2层临界频率foF2时间序列进行了混沌特性的判别，确定其时间延迟和嵌入维数.应用小数据量法计算最大Lyapunov指数，得到λ=0.1264，表明foF2时间序列具有混沌特性.

(2) RBF神经网络短期预报foF2的均方根误差和平均相对误差分别为0.453MHz和4.13%， Volterra模型预报的均方根误差和平均相对误差分别为0.470MHz和4.28%. RBF神经网络预报结果较Volterra级数模型分别提高了0.017MHz和0.15%，较IRI模型分别提高了0.914MHz和6.58%.两者都比IRI模型有较大提高，但RBF神经网络预测性能要稍强于Volterra级数模型.

(3)利用RBF神经网络进行预测存在一个时间尺度，在24h内的预报效果要好于IRI模型.随着预测时间延长，预测的准确性将会降低.

电离层本身是一个十分复杂的非线性系统.电离层中各参量不仅受到大气层中各种气象活动的影响，磁层、太阳活动以及各种宇宙射线也会对其造成很大影响，各参量也会相互作用，相互影响，因此对电离层的精准预测是十分困难的一件事.通过混沌理论研究foF2的变化规律，为探究电离层的变化规律提供了一种新的思路.在对foF2的研究中，混沌预测可与其他的预测方法相互借鉴，综合运用，充分发挥各种预测方法的优势，以期达到更好的效果.