对两圆的幂之比为定值的点的轨迹方程

陕西省陕西师范大学附属中学(710061) 李朋涛

摘要到两定点的距离之比为定值λ(λ/=1)的点的轨迹为圆,称为阿波罗尼圆[1].本文受此启发,将此结论推广为:对两定圆的幂之比为定值的点的轨迹,并得到了相应的轨迹方程.

1.知识介绍

点对圆的幂定义:点P对⊙O的幂为|PO|2-r2,其中r为⊙O的半径.注意当点P在⊙O外时,P对⊙O的幂|PO|2-r2为过P的⊙O的切线长的平方.

引理1对两圆的幂相等的点的轨迹是一条垂直于连心线的直线.

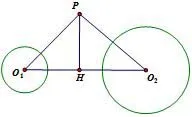
图1

证明设点P对⊙O1、⊙O2的幂相等,作PH⊥O1O2,垂足为H.记|O1O2|=d,|O1H|=d1,|O2H|=d2,则d=d1+d2.由点对圆的幂的定义知即,所以即由方程组解得:这个结果与点P无关,即不论点P的位置如何,H均为一固定点,这表明点P在O1O2的过H的垂线上.反之,因上面的证明可逆,所以这条直线上的任意一点关于这两圆的幂相等.这条直线—对两圆的幂相等的点的轨迹,称为这两圆的根轴.(有关两圆根轴的更多内容请参见文献[2].)

定理1两圆⊙O1:(x-a1)2+(y-b1)2=,⊙O2:(x-a2)2+(y-b2)2=的根轴方程为两圆方程之差.

证明由引理知两圆根轴为垂直于连心线的直线,设P(x,y)为两圆根轴所在直线上任一点,由根轴的定义知点P到两圆的幂相等,即化简得:此方程即为两圆根轴所在直线的方程,它为两圆方程之差.

由定理1可知,两圆的根轴为垂直于连心线的直线,根轴的方程为两圆方程之差.

定理2到两定圆的幂之比为定值λ的点的轨迹为圆(当λ=1时为直线),且该圆与两定圆共根轴.

证明设两定圆为⊙O1:(x-a1)2+(y-b1)2=,⊙O2:(x-a2)2+(y-b2)2=,动点P(x,y)对两定圆的幂之比为定值λ,则由点对圆的幂的定义有整理得:(1-λ)x2+(1-λ)y2+2(λa2-a1)x+2(λb2-b1)y=当λ=1时,动点P轨迹方程为:注意到此方程为两圆方程之差,即⊙O1与⊙O2的根轴.

当λ/=1时,化简得动点P的轨迹为圆:

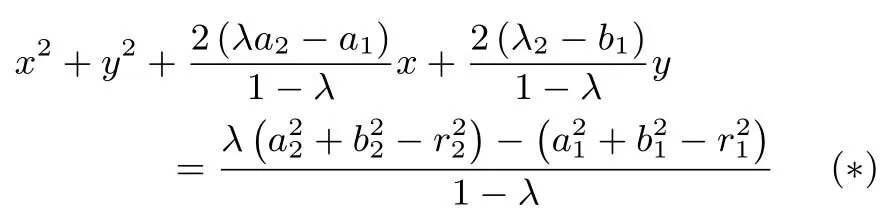
由定理1知两圆根轴为两圆方程之差,故该圆与⊙O1的根轴方程为:化简得这与⊙O1、⊙O2的根轴相同,即三圆共根轴,证毕.

推论1当两圆之一变为点圆时,结论仍成立;特别地当两圆均变为点圆时,结论也成立,此时的圆(*)被称之为阿波罗尼圆.(与阿波罗尼圆有关的更多性质请参见文献[3].)

2.应用举例

例1(1994年全国高考)已知点Q(2,0)和⊙C:x2+y2=1,动点M到⊙C的切线长与|MQ|的比值λ(λ＞0),求动点M的轨迹方程.

解因动点M到⊙C的切线长与|MQ|的比值为λ,所以动点M对⊙C与点圆Q(2,0)的幂之比为λ2.当λ=1时,动点M的轨迹即为⊙C:x2+y2=1与点圆⊙Q:(x-2)2+y2=0的根轴,由推论1知此时动点M的轨迹方程为两圆方程之差,即直线:当λ/=1时,由定理2知此时动点M的轨迹为圆,由式(*)立即得动点M的轨迹方程为:

例2(2005年高考江苏卷)已知⊙O1:(x+2)2+y2=1,⊙O2:(x-2)2+y2=1过动点P分别作⊙O1,⊙O2的切线PM,PN(M,N为切点),使得求动点P的轨迹方程.

解由可知,动点P对⊙O1,⊙O2的幂之比为2,所以由定理2知动点P的轨迹为圆,由式(*)立即得动点P的轨迹方程为:x2+y2-12x=-3.

例3(2006年高考四川卷)已知两定点A(-2,0),B(1,0),动点P满足|PA|=2|PB|,求动点P的轨迹方程.

解将定点A(-2,0),B(1,0)看作点圆,因|PA|=2|PB|,所以动点P对两点圆的幂之比为4,由定理2知动点P的轨迹为圆,由式(*)立即得动点P的轨迹方程为:x2+y2-4x=0.

例4(2013年高考江苏卷)已知A(0,3),圆C的半径为1,圆心在直线y=2x-4上,若圆C上存在点M,使得MA=2MO,求圆心C的横坐标a的取值范围.

解由题设知圆C方程为:(x-a)2+(y-2a+4)2=1,将点A(0,3),O(0,0)看作点圆,因MA=2MO,故点M对两圆的幂之比为4,由式(*)立即得动点M的轨迹方程为:x2+(y+1)2=4,又因动点M亦在圆C上,故只需两圆有公共点即可.即解得

例5(2012年全国高中数学联赛福建省预赛试题)已知圆C:(x-2)2+(y-2)2=m,点A(4,6)和点B(s,t).若s,t为正整数且圆C上任一点到点A的距离与到点B的距离之比为定值λ(λ＞1),求m的值.

解将点A(4,6),B(s,t)看作点圆,由式(*)立即得对两(圆的幂之)比为定值λ2的点的轨迹为圆:x2+由题知该圆与圆C:x2+y2-4x-4y=m-8重合,即注意到s,t为正整数,解得s=3,t=4,λ2=2,所以即m-8=2,解得:m=10.

例6(2011年卓越联盟自主招生试题)在△ABC中,AB=2AC,AD是∠A的平分线,且AD=kAC.

(1)求k的取值范围;

(2)若S△ABC=1,问当k为何值时,BC最短?

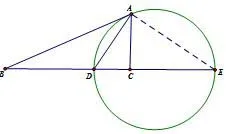
图2

解 (1)方法一满足AB=2AC的点A的轨迹为阿波罗尼圆,过A作AE⊥AD,交BC 延长线于E,由阿波罗尼圆的几何意义知,点A的轨迹为以DE为直径的圆,如图2所示.在△ABC中由张角定理得解得当点A在圆上运动时

方法二以BC为x轴,BC中垂线为y轴建立直角坐标系.设B(-c,0),C(c,0),将点B、C看作点圆,因AB=2AC,故点A的轨迹为对两圆的幂之比为4的点的轨迹,由式(*)立即得A(x,y)的轨迹阿波罗尼圆,其方程为:由角平分线定理可知:,所以从而

(2)当△ABC的BC边上的高为阿波罗尼圆半径时BC最短,由(1)方法二中A的阿波罗尼圆方程知则从而

例7(2012年辽宁省五校协作体竞赛试题)已知圆C:x2+y2=9,点A(-5,0),若在直线OA上存在定点B(不同于点A),满足:对于圆C上任一点P,都有为一常数,试求所有满足条件的点B的坐标.

解设B(b,0),由式(*)立即得到对两点圆B(b,0),A(-5,0)的幂之比为λ的点的轨迹是圆:它与圆C:x2+y2=9是同一个圆.所以解得故当时,对于圆C:x2+y2=9上任一点P,都有

例8(2017年中国女子数学奥林匹克试题)四边形ABCD内接于⊙O,⊙P分别切AC、BD于点E、F,交⊙O于S、T两点,直线FE交AD于M,交BC于N,证明:M、N、S、T四点共圆.

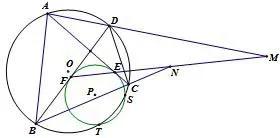
图3

证明因⊙O与⊙P的根轴为直线ST,故要证M、N、S、T四点共圆等价于证⊙O,⊙P及△MNS的外接圆三圆共轴即可.根据定理2只需证明:而sin∠NEC=sin∠AEM,sin∠NEC=sin∠MFD,sin∠NBF=sin∠MAE,sin∠NCE=sin∠MDF,证毕.(此解答由文武光华工作室田开斌老师提供.)