不平衡量对弹丸膛内稳定性影响的仿真分析*

廖 伟,蒋建伟,邱 浩,王 昕,彭嘉诚

(北京理工大学爆炸科学与技术国家重点实验室, 北京 100081)

0 引言

由于炮膛内壁与弹丸定心部之间存在弹炮间隙,并且在弹带机械磨损和火药气体冲刷下,弹炮间隙还会增大[1],使得弹丸可以做偏离炮膛轴线的俯仰、侧摆运动[2]。弹药在加工及装配过程中还可能存在误差,若存在偏心质量会在弹丸旋转时产生离心力[3],从而导致弹丸定心部与身管发生碰撞,出炮口后产生攻角,严重影响火炮射击精度[4]。

刘雷[5]将弹丸假设为刚体,身管视为弹性体,建立身管和弹丸刚柔耦合动力学模型,分析了身管的动力响应。许耀峰等[6]基于弹塑性有限元理论,建立有限元模型并分析了不同膛线类型下弹炮动力学响应。马明迪等[7]基于有限元与光滑粒子耦合算法,对初始装填角、弹炮间隙、装填不到位等因素对挤进过程进行了研究。膛内运动过程较难通过试验进行观测,基于有限元理论的身管弹丸耦合动力学仿真已成为研究膛内运动的主要手段,但目前研究弹丸膛内稳定性的工作较少,并且没有适用于表征弹丸膛内不稳定性的参量。

文中以弹丸膛内运动过程为研究对象,基于弹塑性有限元理论,建立火炮身管弹丸耦合的动力学有限元模型。对偏心质量形成静不平衡和力偶不平衡两种典型状态进行仿真研究,得到了弹丸横向过载、章动角和弹炮轴线距随行程的变化规律。

1 参量定义

1.1 不平衡量定义

线膛炮在发射过程中,弹丸沿身管向前运动的同时旋转,其稳定性主要受弹丸结构中静不平衡和动不平衡量影响。文中研究的静不平衡量为弹丸偏心距,如图1(a)所示,指弹丸质心偏离轴线的距离。动不平衡量为不平衡力偶[8],指弹丸所有质量单元离心力系的合成力偶,如图1(b)存在两处偏心质量,当它们满足式(1)时,弹丸偏心距为零,但转动时会形成大小如式(2)所示的力偶矩。

图1 弹丸不平衡典型情况

(1)

T=M1e1ω2L=M2e2ω2L

(2)

式中:T为力偶矩;ω为弹丸角速度;L为力臂。

排除式(2)中与弹丸结构无关的角速度因素,定义弹丸力偶不平衡量为:

(3)

1.2 不稳定量定义

不稳定量是指弹丸膛内不稳定性的度量,为本研究的因变量,包括横向过载、章动角及弹炮轴线距。如图2所示,横向过载是弹丸垂直于炮膛轴线方向上的加速度,可以表征弹丸对身管侧壁冲击作用强弱;章动角是指弹丸几何轴线与炮膛几何轴线的夹角,用以表征弹丸摆动幅度的大小;弹炮轴线距是弹丸几何轴线与炮膛几何轴线的距离,用以表征弹丸偏离炮膛轴线的程度。

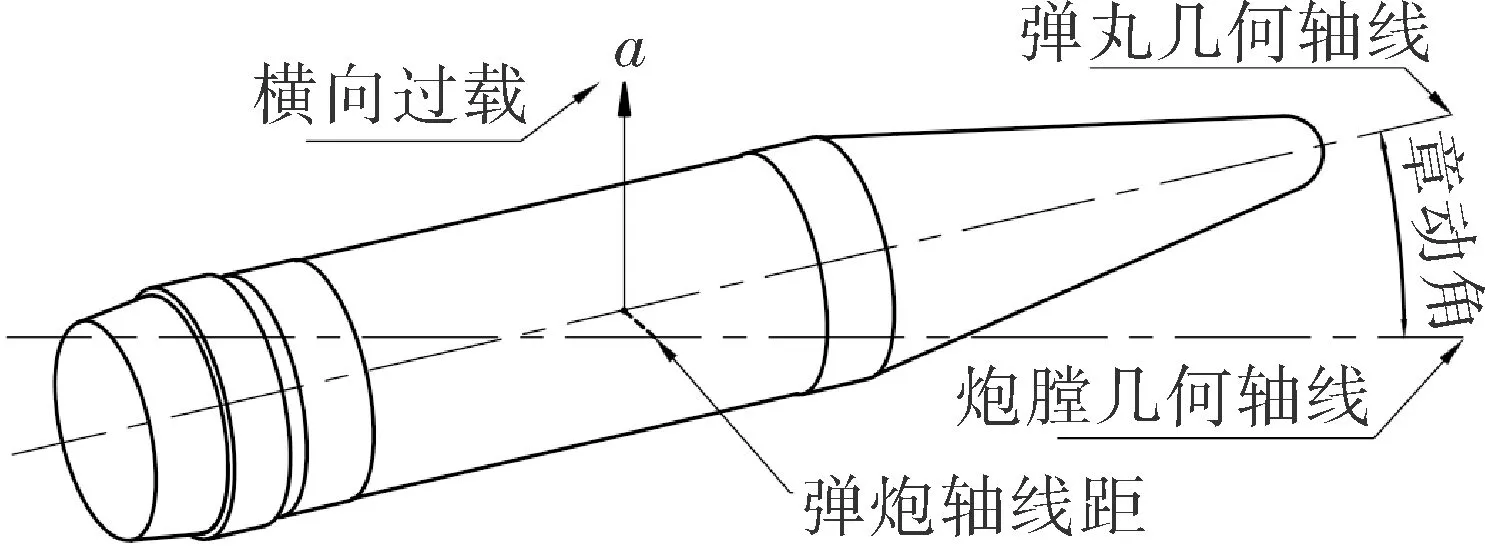
图2 弹丸不稳定量示意图

2 仿真模型

2.1 有限元模型

采用30 mm火炮的榴弹发射过程为研究对象,身管使用等齐膛线,缠角6.3°,榴弹弹丸由引信、炸药、弹体和弹带4部分组成,弹重395 g,弹丸定心部与炮膛内壁初始间隙为0.025 mm。弹丸和身管均采用Solid164六面体Lagrange单元算法,建立的身管及榴弹有限元模型如图3、图4所示。

应用ANSYS/LS-DYNA显示动力学分析软件进行计算。通过调整弹丸两侧壳体密度来设置偏心距,通过在质心前后对称位置添加偏心质量来设置不平衡力偶。弹带与膛线接触使用侵蚀接触算法,能更好的模拟挤进过程中弹带的剪切磨损。

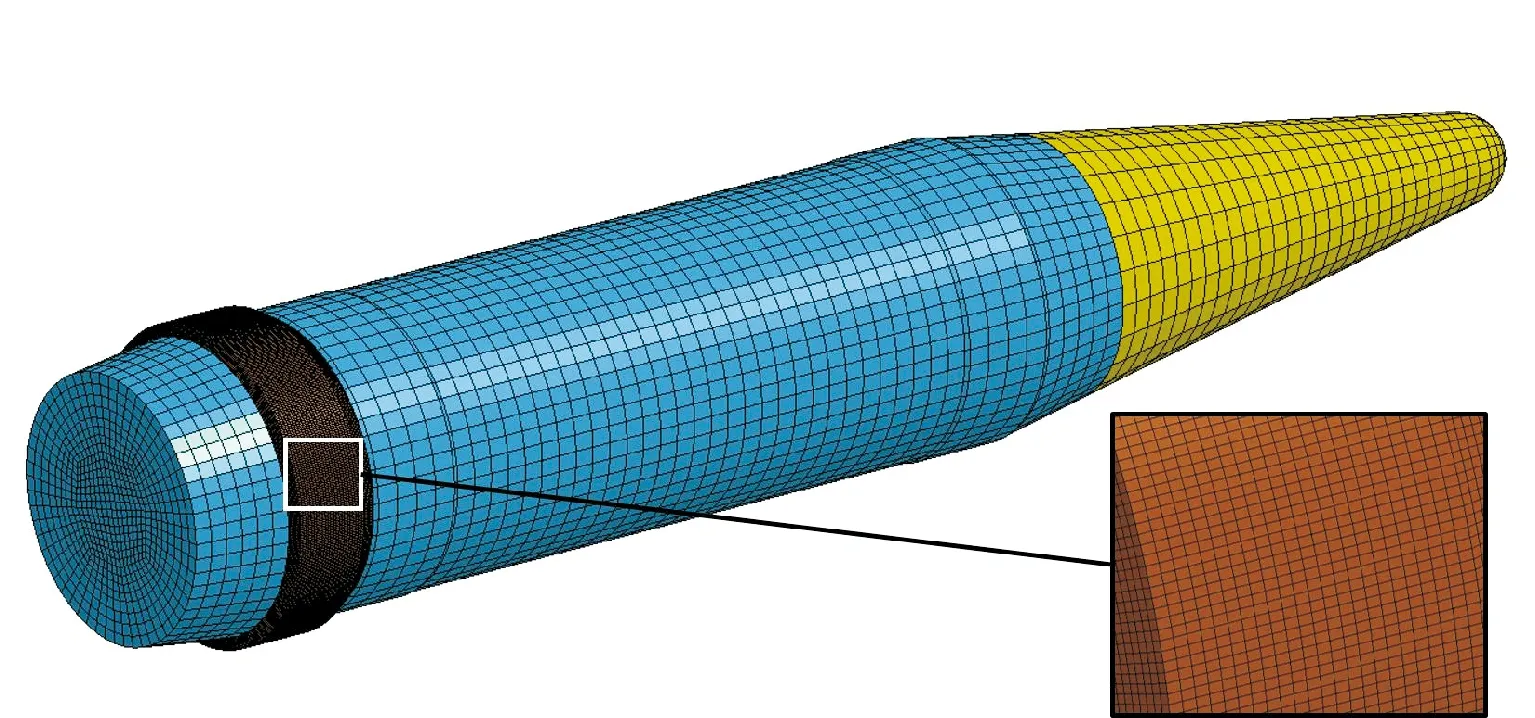
图3 弹丸有限元模型

图4 身管有限元模型(坡膛剖面)

2.2 材料模型

弹带材料为紫铜,采用如式(4)所示的塑性随动硬化模型,表1为紫铜的材料参数,其余部件材料均采用双线性随动硬化模型。

(4)

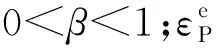
表1 弹带材料参数[11]

弹带采用应变失效准则,即当单元达到模型预先设定的失效应变时,单元失效并被程序自动删除。Matsuyama、Lisov等人的研究表明[9-10],弹带与身管间的摩擦系数并不是常数,满足如下关系:

(5)

式中:μ为摩擦系数;λp为弹带导热系数;Tmp为弹带熔点;T0为初始温度;P为接触面压力;V为相对速度;ap为弹带热扩散系数;Hp为弹带宽度。

弹带与身管的摩擦系数对仿真结果如弹丸速度的影响不可忽略,使用*DEFINE_TABLE命令将其关系式(5)嵌入仿真程序,模拟摩擦系数随温度升高而变化的过程,表2为弹带的热力学参数。

表2 弹带热力学性能参数

2.3 载荷、边界条件及观测点设置

将压力施加于弹丸底部所有作用面上,模拟火药气体对弹丸的作用过程。图5是仿真使用的弹底压力-时间曲线,为某30 mm榴弹实测数据,峰值压力约为300 MPa。并在身管尾端面添加3个方向的自由度的约束,同时在弹丸中心轴线上设置如图6所示的两个观测点,分别位于弹头部和底部的轴线上,用于计算弹丸位移、速度、章动角等参量。

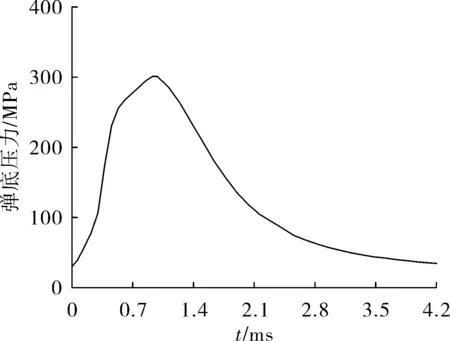
图5 弹底压力-时间曲线

图6 观测点位置

2.4 模型验证

基于上述模型对正常条件下的榴弹发射过程进行仿真,计算得到的弹丸行程-时间曲线、速度-时间曲线如图7、图8所示,与该弹实测值误差均在1%以内。图9为典型时刻的弹丸受力状态。

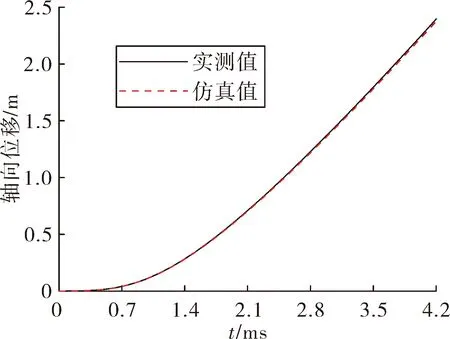
图7 行程-时间曲线

图8 速度-时间曲线

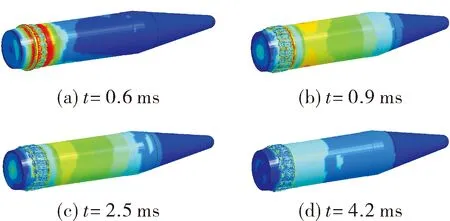
图9 典型时刻的弹丸状态

3 仿真结果与分析

3.1 不同静不平衡条件下的仿真

通过调整弹丸两侧壳体密度的方法来调整弹丸初始偏心距,分别设置和计算了偏心距分别为0 mm、0.07 mm、0.14 mm、0.21 mm 4种条件,得到弹丸的横向过载-行程曲线、章动角-行程曲线、弹炮轴线距-行程曲线,分别如图10～图12所示。由图10可知：弹丸横向过载在初始阶段有一定波动,在0.3～2.4 m区间内(约1.7～4.2 ms)逐渐稳定上升,其提升幅度在不同偏心距条件下呈现明显倍数关系,说明弹丸横向过载与偏心距成正比。横向过载在炮口达到最大值,此规律能解释小口径火炮常在炮口处出现膛线破坏的现象。由图11可知：章动角在弹丸启动时便达到峰值,在0～0.5 m区间内(约0～2.1 ms)振幅较大,在0.5～2.4 m区间内(约2.1～4.2 ms)保持稳定并平缓上升,并且偏心距越大章动角越大。由图12可知：弹炮轴线距在弹丸启动时便达到峰值,在0.01～2.4 m区间内(约0.7～4.2 ms)逐渐下降并趋于稳定,但其受偏心距的影响小于1/1 000 mm,可忽略不计。不同偏心距条件下各膛内不稳定量的峰值如表3所示,可以看出：弹丸的横向过载、章动角及弹炮轴线距均与偏心距呈正相关。

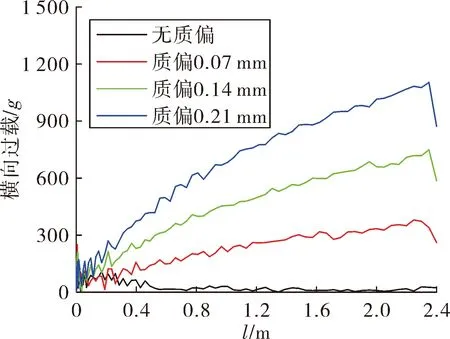
图10 横向过载-行程曲线

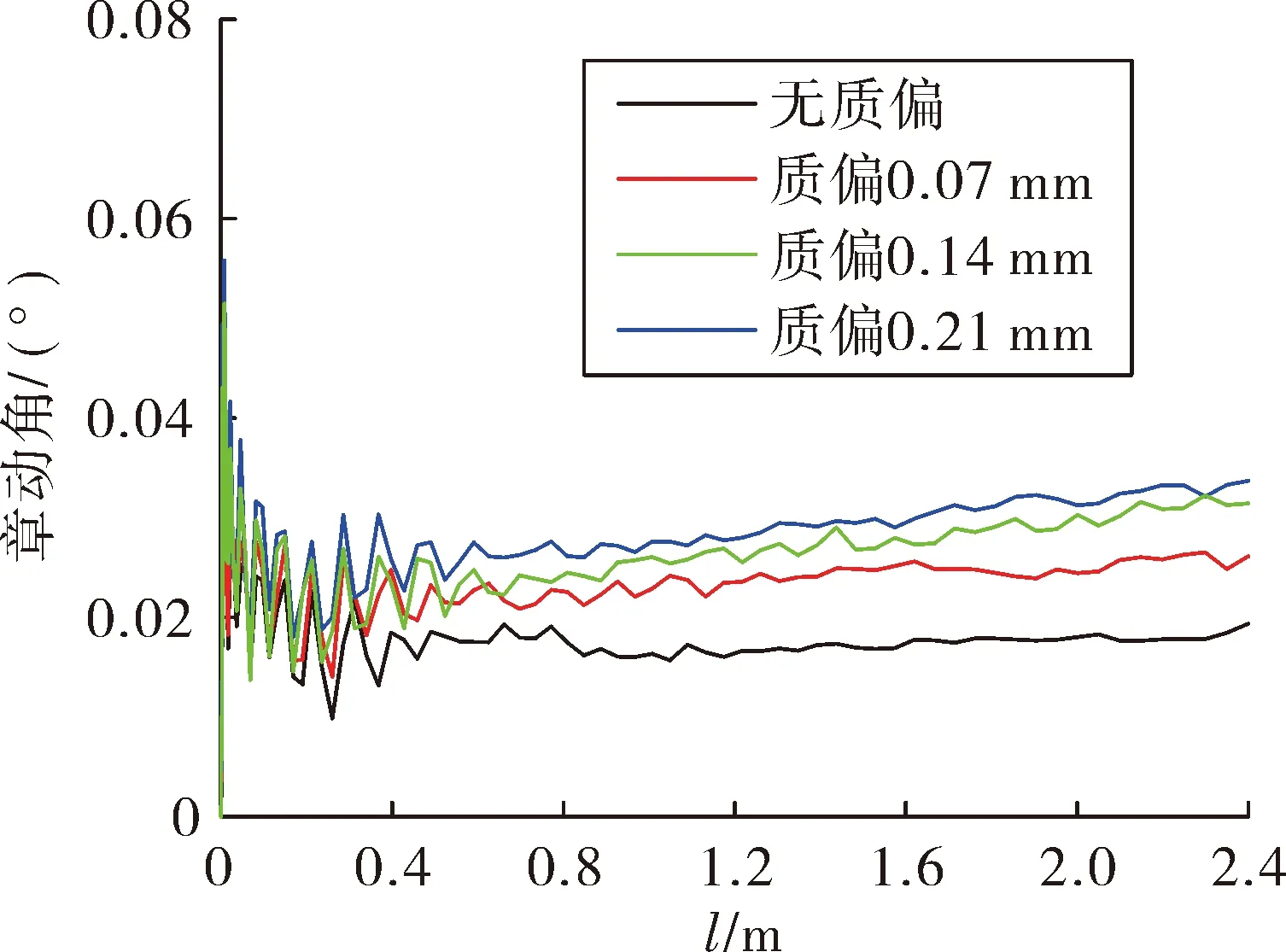
图11 章动角-行程曲线

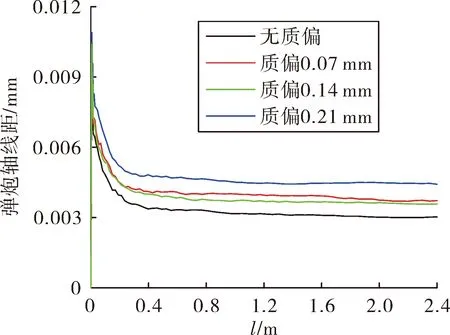
图12 弹炮轴线距-行程曲线

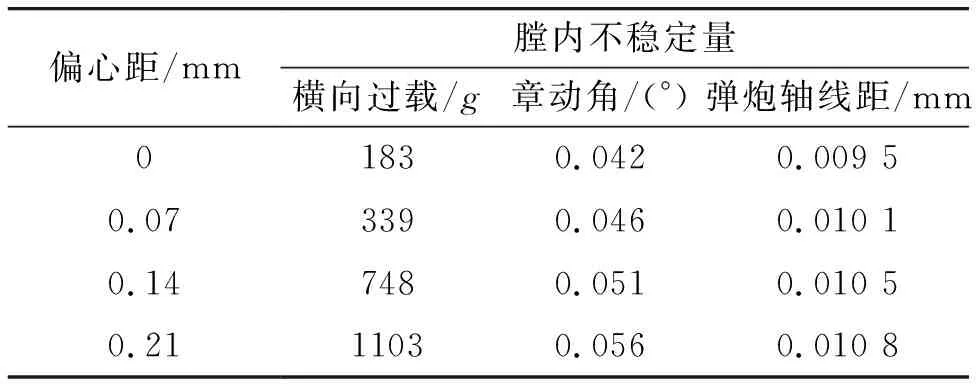
表3 不同偏心距下膛内不稳定量峰值

3.2 不同动不平衡条件下的仿真

通过在质心前后对称位置施加偏心质量的方法来调整力偶不平衡量,设置并计算了力偶不平衡量分别为0 kg·mm2、1.9 kg·mm2、3.8 kg·mm2、5.7 kg·mm24种条件,得到弹丸的横向过载-行程曲线、章动角-行程曲线、弹炮轴线距-行程曲线,分别如图13～图15所示。由图13可知：弹丸横向过载在0～0.8 m区间内(约0～2.5 ms)振幅较大,且4种情况区别不大,但在0.8～2.4 m区间内(约2.5～4.2 ms)逐渐与力偶不平衡量有关,力偶不平衡量对横向过载有明显的增强作用。由图14可知：弹丸章动角一开始便达到峰值,然后震荡衰减,4种情况产生区别开始于0.4～2.4 m区间内(约2～4.2 ms),当有力偶不平衡量时,章动角-行程曲线出现明显减小后增大的“反弹”现象,且力偶不平衡量越大反弹越明显。力偶不平衡量对膛内不稳定量的影响主要出现在膛内运动中后期,各力偶不平衡量条件下炮口处的膛内不稳定量如表4所示,可以看出弹丸炮口横向过载、弹炮轴线距与力偶不平衡量呈正相关。

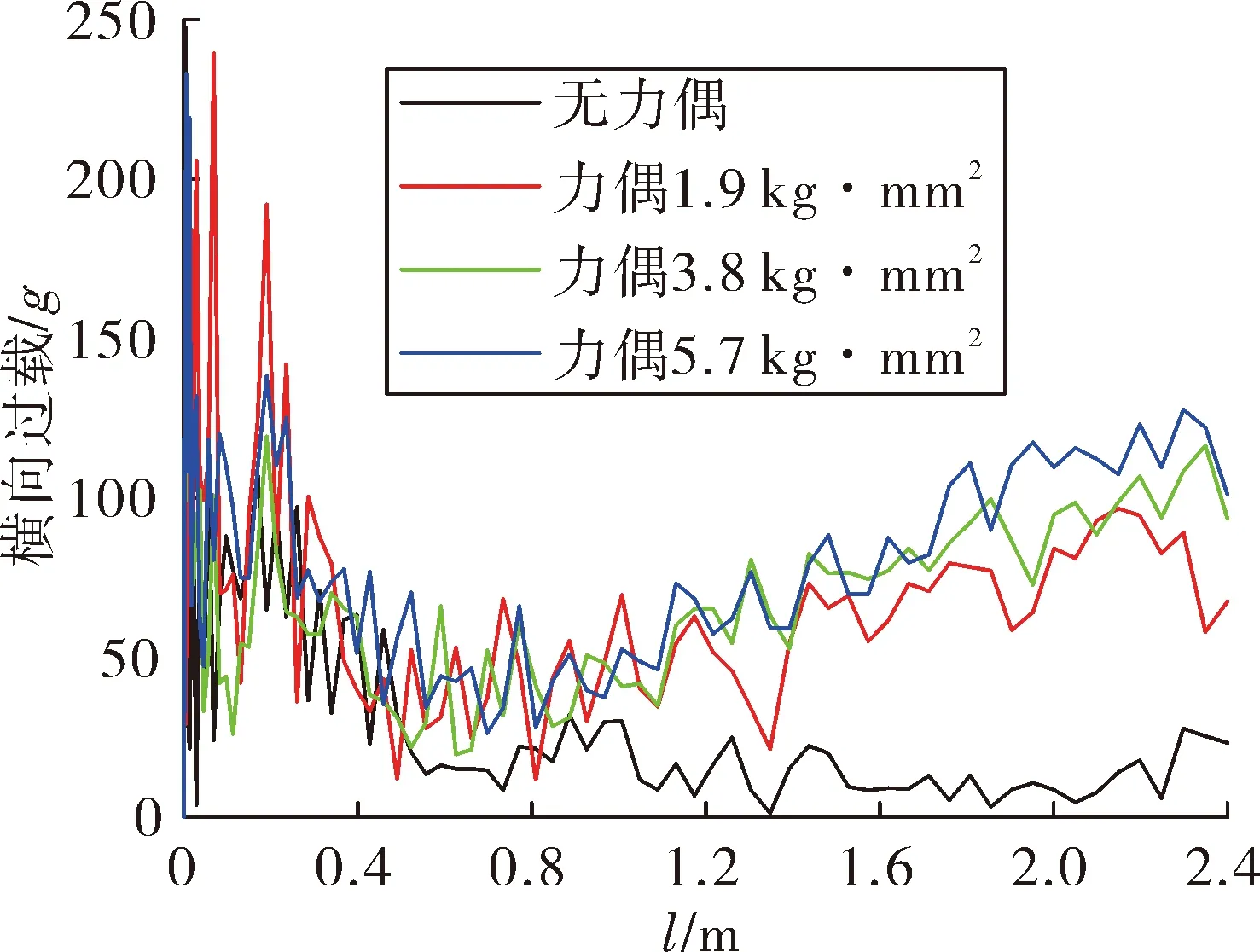
图13 横向过载-行程曲线

图14 章动角-行程曲线

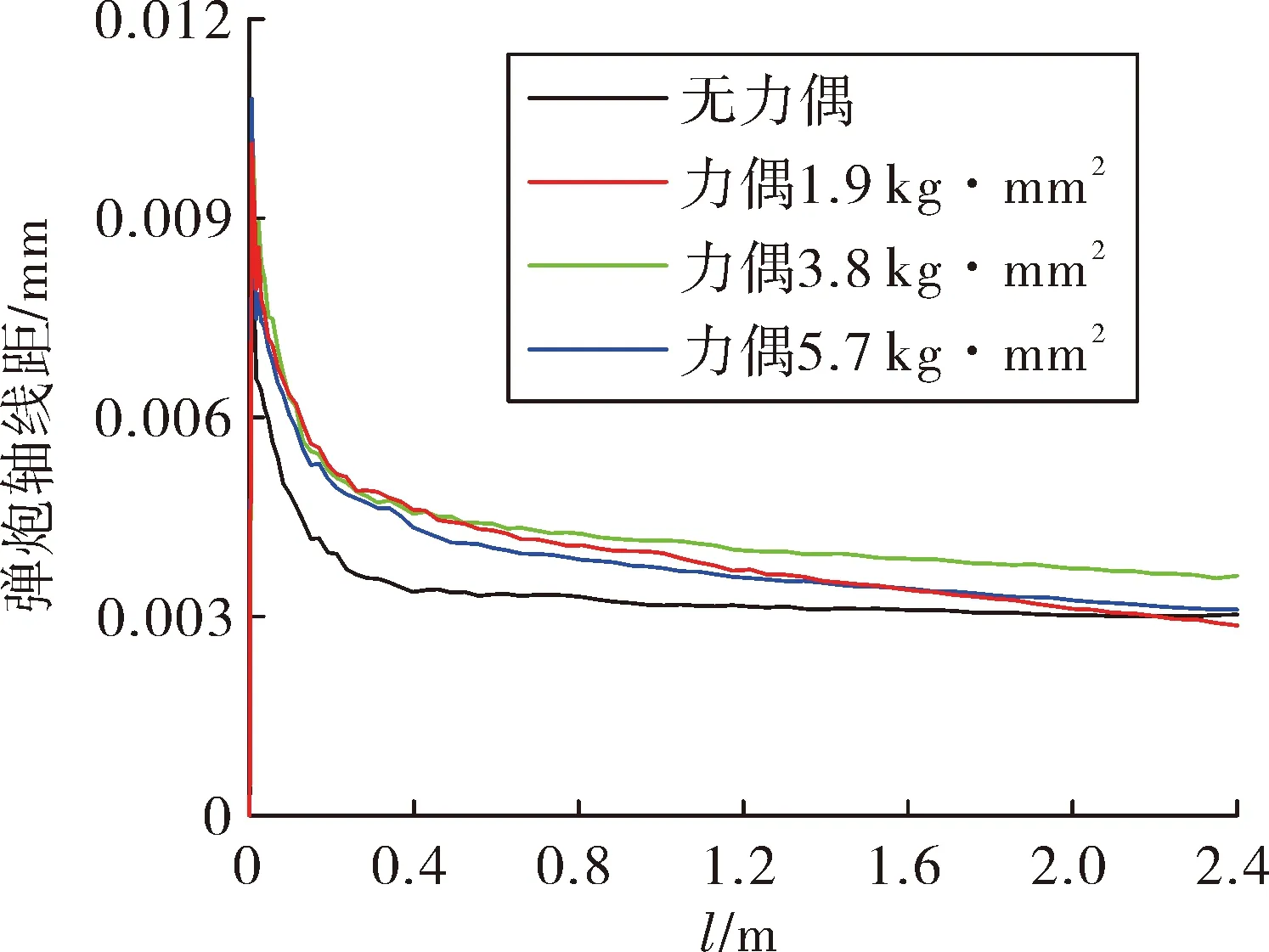
图15 弹炮轴线距-行程曲线

表4 出炮口时刻不同力偶不平衡量下的不稳定量

4 结论

文中以30 mm榴弹弹丸膛内运动过程为研究对象,建立火炮身管和弹丸耦合的动力学有限元模型。分析了弹丸存在偏心距、不平衡力偶的情况下,弹丸膛内的横向过载、章动角和弹炮轴线距的变化规律。得出以下结论:

1)弹丸的横向过载、章动角能很好地反映弹丸在膛内的不稳定运动,适用于研究弹丸膛内不稳定性。弹炮轴线距受不平衡量的影响较小,其可能主要取决于弹炮间隙、弹带材料等因素,有待进一步研究。

2)弹丸偏心距与横向过载近似呈正比关系,并且在炮口处达到最大值(约距炮口5～10 cm处),可能会对膛线造成破坏。

3)不平衡力偶主要影响弹丸膛内运动的中后期(约2.5～4.2 ms),其对弹丸横向过载有明显的增强,对章动角的影响出现先减小后增大的“反弹”现象。