温度载荷下长径比与m数对组合装药结构影响分析*

王晨飞,许进升,陈 雄

(南京理工大学机械工程学院, 南京 210094)

0 引言

为提高固体火箭发动机效能,通常将两种或多种不同燃速的推进剂采取串联的方式组合,进而达到各项指标要求[1]。对于固体火箭发动机来说,其在从制造到发射过程中,会受到很多温度载荷类型,包括温度冲击载荷、固化降温载荷、循环温度载荷等。其中温度冲击载荷对固体火箭发动机中药柱的影响最为显著,因此,需要对此类温度载荷作用下的装药结构完整性展开深入的研究。目前,国内外大部分研究都采用线性粘弹性本构关系来研究贴壁单一形状装药的结构完整性问题[2-3],对于贴壁式组合药柱的装药结构完整性问题研究的较少,这是由于药柱整体外形较为复杂,型面多样,危险点位置随药柱整体形状不固定。随着武器装备的发展,由于复杂型面的药柱可满足固体火箭多种性能指标,必须对其复杂的结构完整性进行探讨分析。

文中针对贴壁式组合药柱,以三维线粘弹性理论为基础,重点分析低温环境下温度冲击载荷的药柱危险点最大应变值对于装药结构完整性的影响。

1 计算模型及数值方法

1.1 有限元基本原理

通过运用位移法,可得出有限元计算方法的矩阵形式[4]:Kc=F

其中,刚度矩阵K可进一步表示成:

K=∭VBTDBdV

式中:D为弹性矩阵;B为节点位移应变矩阵。

1.2 热传导方程及计算模型

文中的模型忽略了热对流以及热辐射这两种热交换基本形式对药柱内温度分布的影响。仅考虑热传导对于药柱的作用,给出了如下的三维导热微分方程:

式中：ρ为密度;c为比热容;T为介质厚度;λ为热传导系数。

从相关数据可以发现,空气导热系数仅为0.023 W/(m·K),其与壳体、药柱和包覆层的导热系数相差较多,且由上述三维导热微分方程可以发现,通过空气传递的热量只是占到整个发动机传递热量的很小一部分。为了简化计算,文中对物理模型进行简化,所得模型忽略发动机外部以及内部空气的传热。

1.3 药柱的破坏经验准则

由于推进剂在低温环境下应变能力较低,而且在药柱的内孔表面处一般会存在较大应变。当进行单向拉伸实验时,如果应变值达到推进剂材料的最大应变能力ε,推进剂内部会出现裂纹,如果裂纹进一步扩大,将会导致推进剂断裂和破坏。因此,最大应变理论通常可以作为药柱破坏的经验判据[5]。

2 物理模型及数值方法

文中针对贴壁式浇铸的固体火箭发动机装药,为了突出研究模型组合装药的长径比与m数对结构完整性的影响,采用的药柱为圆孔以及星孔相结合的组合装药,由于药柱结构的对称性,可以进行适当的简化处理,同时在建立模型时,对固体火箭发动机的部分设置进行了一些简化假设:1)壳体厚度一致,认为壳体均匀;2)绝热层可以视为弹性体,弹性模量固定;3)简化壳体的圆角、倒角部分以及前后端处的封头;4)药柱圆孔与星孔,过渡段处的内孔以及有前后两侧金属块内与应力释放罩空隙处较少部分的空气传热按纯导热处理,不考虑热对流对其的影响。

其中简化模型如图1所示。模型主要包括:发动机壳体、包覆层、药柱、两侧应力释放罩[6-7]以及金属块,其中药柱为圆孔以及星孔的组合装药。在发动机前后两侧使用包覆层作为应力释放结构的材料。

图1 固体火箭发动机结构示意简图

为了分析出药柱的长径比、圆孔段m数以及过渡段角度这几个参数对于装药结构完整性的影响,将药柱的长径比从1到9(每组间隔1),圆孔段m数从3到9(每组间隔1),且星孔段m数不变来进行计算与分析,共计63组数据,且由于药柱存在3种结构(圆孔段、星孔段、过渡段),因此这3种结构的轴向长度采用按比例划分来设计药柱。同时过渡段由于此时的轴向长度的变化,影响到过渡段角度的变化,因此对过渡段角度的变化是否影响装药结构完整性也进行了计算,其中将m数不变,只变化其中一组的过渡段与圆孔段轴向长度来改变角度,角度变化由10°～60°,每次间隔为5°,共11组数据。

2.1 温度载荷

为了与真实情况下的发动机温度冲击载荷试验具有一定的可比性,将计算模型的温度载荷边界条件设置为:在初始状态下,整个发动机试件处于65℃的高温环境中,同时可把此时的药柱认为处于零应力状态。由于在低温环境下固体火箭发动机装药结构发生破坏的可能性极大,采取计算工况为施加-40℃的温度载荷,开始降温,经过一段时间温度降低到-40℃,并保持该温度48 h来使得发动机内部的温度基本达到平衡。

2.2 性能参数

研究中壳体与金属块可采用金属弹性材料,包覆层则选用弹性材料,应力释放罩采用与包覆层一致的弹性材料,见表1。

表1 材料参数

其中复合推进剂是一种粘弹性材料,而且对于大多数的粘弹性材料来说,松弛模量可采用Prony级数的形式来描述。文中药柱的松弛模量可描述为:

药柱时间-温度WLF方程为:

2.3 边界条件

在正常情况下,贴壁浇铸药柱的固体火箭发动机采取自由放置方式,发动机壳体部分的外表面选取为温度边界,两侧面设置采取对称边界条件,设置一侧的金属块的轴向方向来进一步限制其轴向位移。根据图2的模型边界设置,壳体与包覆层采取相互Tie接触,药柱与包覆层接触部分以及与两侧应力释放罩均为Tie接触,两侧应力释放罩与包覆层相互Tie接触,两侧金属块分别与壳体两端面Tie接触,以表示金属块与壳体相互焊接状态。同时冷却过程中,整个发动机仅从外壁面散发热量,其余均为绝热。

图2 模型边界设置

2.4 有限元模型与网格划分

由于该发动机模型尺寸较大,为降低计算工作量,根据模型的对称性选取模型的1/12作为研究的对象。由于存在较不规则的过渡段,所以网格部分采用如图3的8节点六面体线性单元与较不规则段采用4节点线形四面体单元相结合的方式进行划分,单元节点总数由于长径比的不同划分为30 000～100 000不等。

图3 有限元模型与网格划分

3 计算结果与分析

以整段药柱长径比为5、圆孔段m数为6为例建立发动机模型,温度载荷在5 s内由338 K降低到233 K。通过48 h的数值计算仿真,可得到不同时刻温度下装药即时温度分布云图，如图4所示。

当发动机内部药柱温度基本达到平衡时,其变形也就趋于稳定,此时药柱的应变也趋于稳定,且达到最大值,此时药柱内的应变响应也是最为严重的,可以把此时最大应变值的位置称为危险点位置。通过仿真分析可发现,当温度载荷加载48 h后,发动机内外温度基本达到平衡状态,即整个药柱也基本达到平衡状态。其中温度载荷由壳体表面向着包覆层一侧传递,再经由药柱传递过程中,药柱温度逐渐向两侧传递,由于圆孔段所占据长度较多,因此星孔段传递较快,先达到平衡温度,最后圆孔段也基本达到平衡温度。

图4 发动机内部药柱不同时刻的温度分布云图

采用图3所示的网格划分,取长径比为5、圆孔段m数为6的药柱进行仿真，结果见图5，危险点位置出现在圆柱段内孔表面,最大应变值为15.76%,过大药柱的应变可能会导致药柱内表面发生较大形变甚至产生裂纹而导致破坏,对于发动机产生安全隐患,因此需要保证药柱最大应变在一定范围内。

图5 药柱最大应变值图

由于63种有限元模型的星孔段参数不变,仅仅改变圆孔段参数,过渡段斜线处的角度将导致变化,为证实此处对于药柱最大应变值是否产生影响,将此处的角度(10°～60°)划分每5° 一组,共11组数据，且保持长径比、圆孔段m数不变进行计算分析,药柱最大应变值随角度变化关系如图6。

图6 药柱内孔最大应变值随角度变化关系图

从图6可发现,角度递增对最大应变值的影响不显著,说明过渡段角度对药柱最大应变值影响不显著。

图7 药柱不同m数下的应力、应变历程

从图7可以发现,随着药柱的圆孔段m数的增大,整个药柱内部的温度到达开始平衡时所需的时间也越长,因此药柱内表面危险点位置的应力、应变达到平衡所需的时间也越长。同时,从图中可见,药柱的应变值保持了一段时间的平衡,说明此时的值为药柱的最大应变值。

通过上述分析排除过渡段角度对于药柱的最大应变值影响,为了描述出63种计算模型药柱内孔表面危险点的最大应变值的情况,图8显示了63组药柱危险点位置仿真结果的最大应变值。

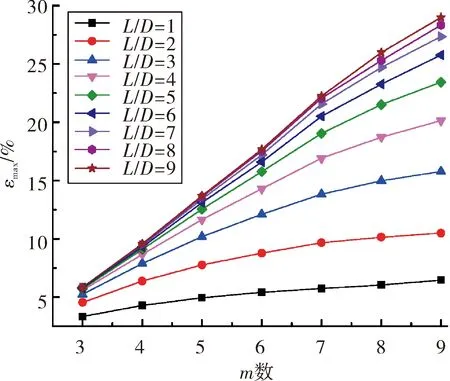
图8 药柱最大应变值随圆孔段m数及长径比变化关系图

4 结论

1)随着圆孔段m数的增大,药柱内温度达到开始平衡时所需的时间越长,因此药柱危险点的应力、应变达到平衡所需的时间也越长。

2)对于贴壁浇铸的固体火箭发动机组合装药来说,在低温环境下的最大应变值与长径比以及圆孔段m数均存在着关系。其中长径比越大,相同圆孔段m数下的最大应变值也越大。相同长径比的药柱,随着圆孔段m数的增加,最大应变值而逐渐增大,最大应变值随着圆孔段m数的增长到一定范围最后而趋于稳定。

3)当药柱的长径比大于4时,圆孔段m数的变化对于药柱的最大应变值的影响起到了主要的作用,长径比的作用开始减弱,而且中间过渡段的斜线处角度影响不显著。

4)对于整段结构为细长型的装药来说,在考虑装药的结构完整性时,工程中通常可以简化部分参数,通过利用m数的值来判断装药结构的完整性,且需要判断药柱的最大应变值是否超过药柱的许用应变,如果超过许用应变可能导致药柱的破坏，影响固体火箭发动机整体的结构完整性。