高压载荷下柔性喷管的力学特性试验与有限元分析*

邹 杰,郑 庆,童 悦,李修明,薛潇潇

(上海航天动力技术研究所, 上海 201108)

0 引言

大推力、高机动性能是导弹武器的必要战术指标。因此提高燃烧室压力,采用推力矢量控制(TVC)技术成为有效的解决方案。其中柔性喷管以其结构简单、推力损失小、响应迅速等优点受到各国青睐,广泛运用在大型战术导弹和助推器上,如欧洲Aster-30导弹助推器、美国SM-3的第三级发动机都采用了柔性喷管作为其推力矢量控制形式[1-2]。

柔性喷管的柔性接头由固定体、活动体、增强件和弹性件组成,增强件和弹性件呈交错粘接排列。柔性接头承受的载荷有燃烧室压力载荷和伺服机构的摆动载荷,随着容压的增大,摆动力矩会在一定范围内有所下降,甚至出现负力矩和结构失稳的现象,长期以来,众多学者认为是超弹性材料在受到轴向压缩情况下,其剪切模量减小所致[3-4],而文献[5]通过大量的试验证明了弹性件橡胶材料的剪切模量并没有随压力增加而减小。由此可见,对于柔性接头摆动力矩产生的内在原因及机理还未形成共识,有待进一步探讨。

研究高压载荷下柔性接头摆动性能可以为导弹飞行控制提供依据,并为柔性接头的设计提供有益的参考。文中通过试验与仿真对照的方法探究了柔性接头工程应用中轴向压缩位移、摆动力矩、接头层间应力、应变与失效模式的内在联系。

1 物理模型与计算方法

柔性接头结构是由接头球半径a、接头角β、接头内外角差β2-β1、接头锥角φ、弹性件层数ne、弹性件厚度te、增强件厚度tr等7个独立参数共同确定的。如图 1所示,基本结构参数见表1。

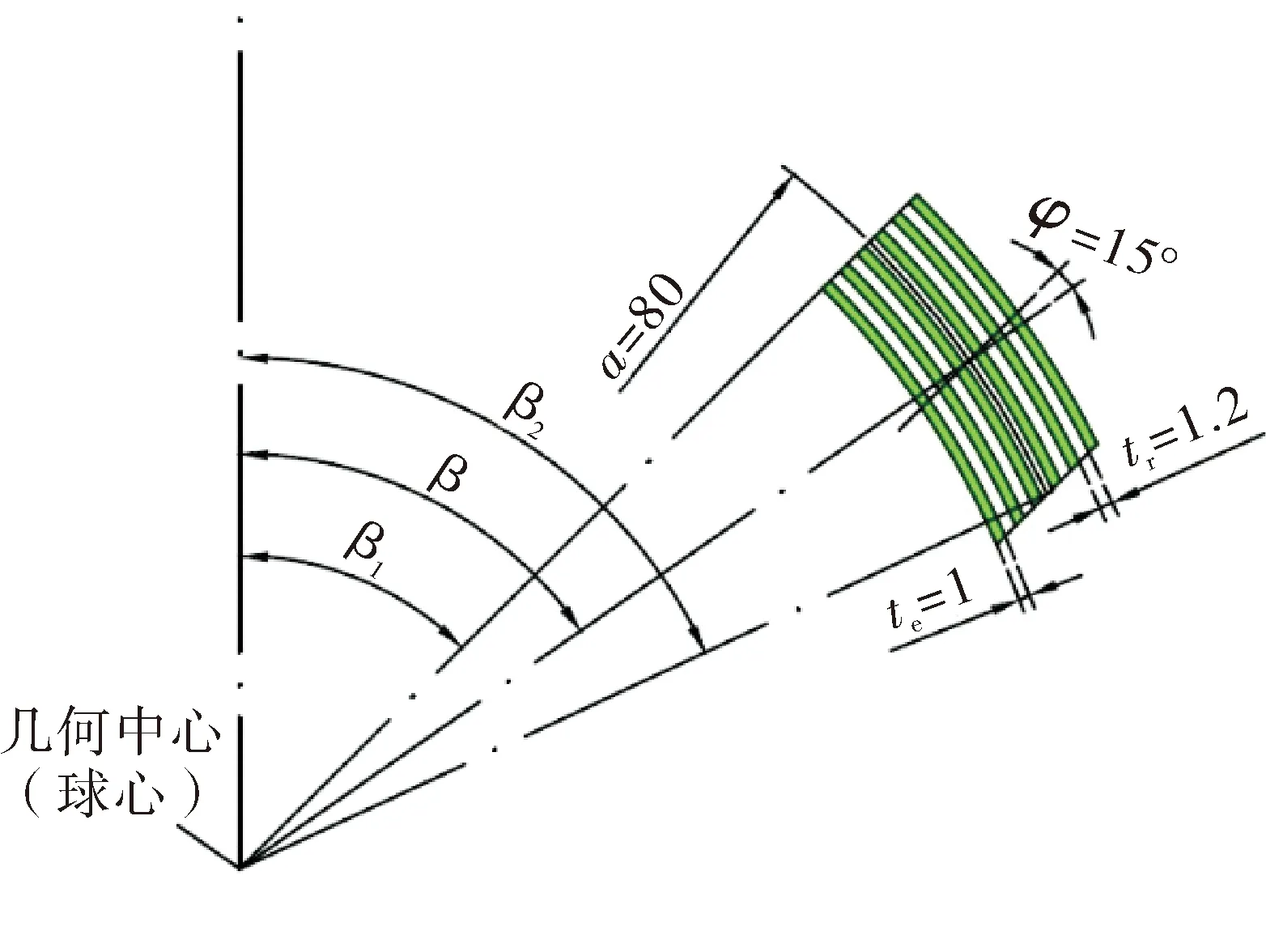
图1 柔性接头结构示意图

表1 柔性接头结构参数

柔性接头冷气试验系统如图2所示。压力容器连接高压气瓶模拟工作压力载荷,通过液压伺服系统驱动柔性接头按预定程序周期性摆动,两个水平位移传感器用于测试摆角,竖直位移传感器结合水平传感器可捕捉轴向压缩位移和摆心,力传感器用于测试伺服机构作动力,结合摆心即可计算作动力矩。

图2 柔性接头摆动试验台

文中通过有限元分析计算了某型号柔性接头在高压载荷下的摆动响应过程。柔性接头进行平面摆动时,几何构型与作用载荷关于作动平面对称,因此在对柔性接头摆动特性进行有限元分析时可以对模型进行适当简化,只建立1/2模型,如图3所示。该模型共约112 000个单元,其中增强件和弹性件沿厚度方向划分2层网格,弹性件橡胶材料全部采用杂交C3D8H单元,增强件、活动体及固定体等金属件采用减缩积分单元C3D8R模拟,承压盖板使用刚体R3D4单元。

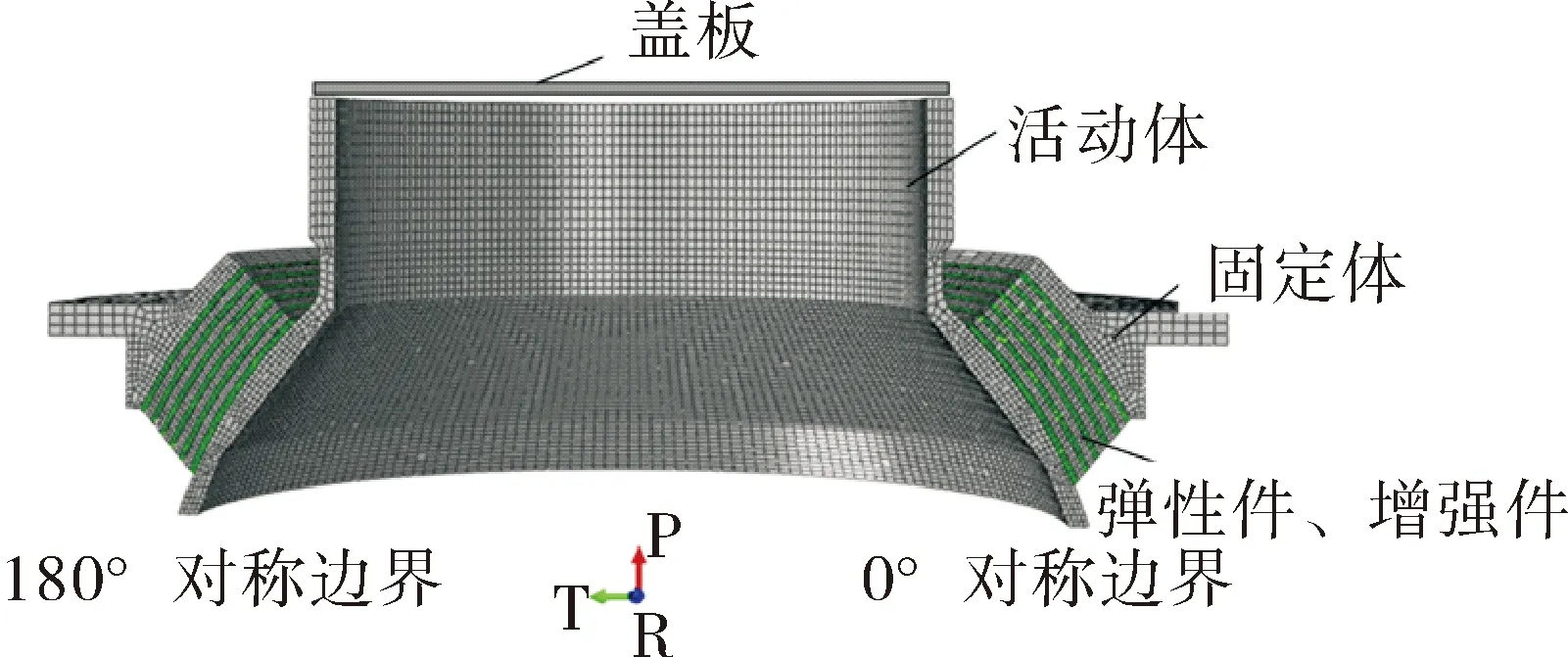
图3 柔性接头有限元模型

对称面φ=0°、180°施加位移对称边界条件,在固定体前后法兰面上施加固定约束。压力载荷均匀作用于活动体所有内部表面。在其顶面中心处设置关键点,建立与活动体之间的刚性连接,在其上施加集中力载荷以实现柔性接头驱动力载荷加载。

增强件及前后法兰材料05Cr17Ni4Cu4Nb为线弹性材料,其弹性模量E=1.97 GPa,泊松比μ=0.29,屈服强度σs=863 MPa。弹性件材料力学特性由ODGEN二阶本构模型表征。

ODGEN模型应变能密度函数如下式[6-7]:

(1)

式中:Di、αi和μi为待定材料模型参数;λ1、λ2和λ3为主伸长率;J为弹性体积比,当材料不可压缩时,J=1。

利用橡胶材料的单轴拉伸、平面剪切试验数据拟合得出ODGEN二阶本构方程系数,见表2。图4、图5为橡胶材料试验数据。

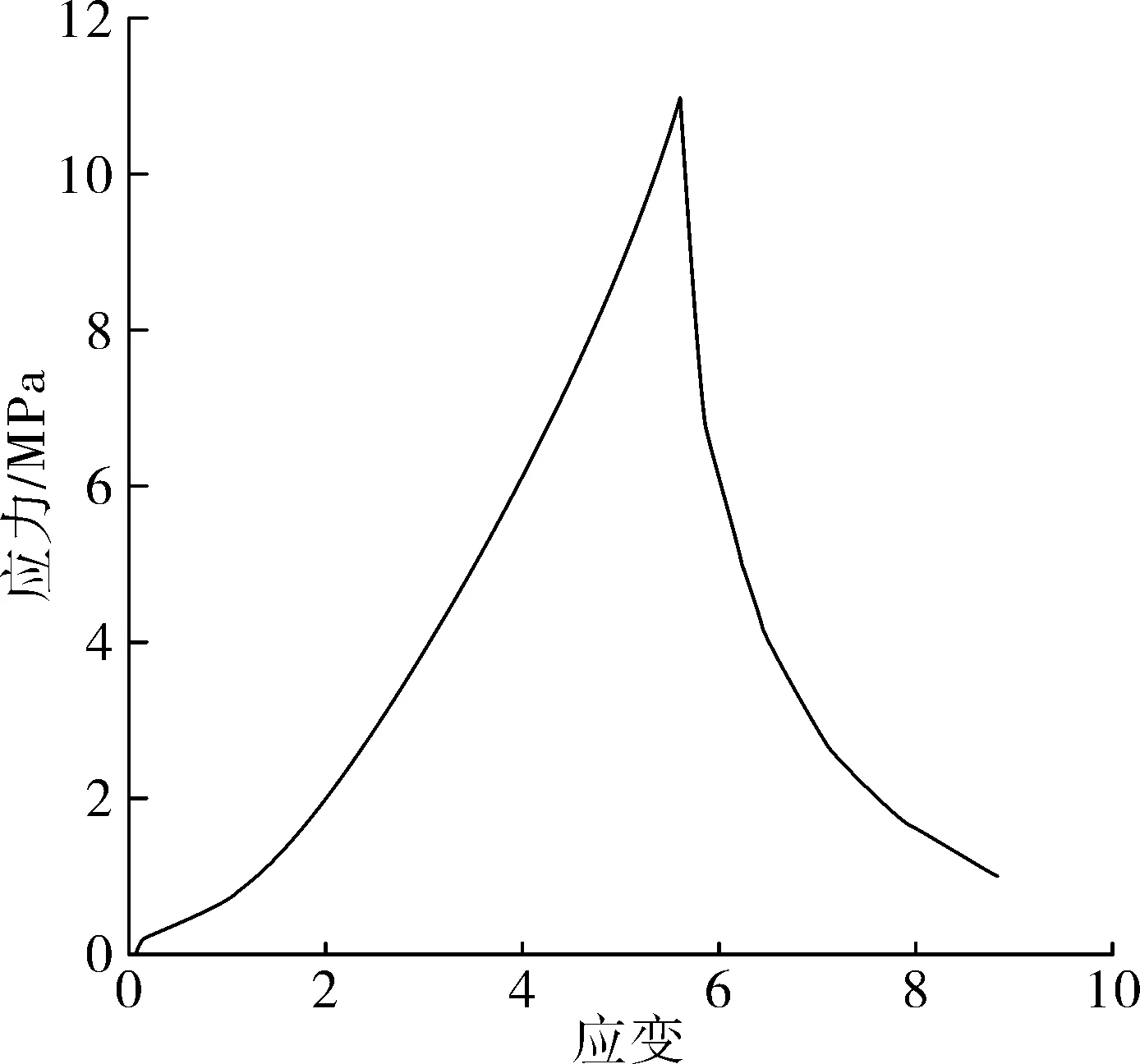
图4 拉伸应力应变曲线

表2 橡胶超弹性材料参数

2 计算结果与分析

超弹性材料应力-应变行为呈现高度非线性,进行包含弹性件的柔性接头的结构特性有限元仿真时,要同时解决橡胶弹性件的材料非线性问题和柔性接头几何结构的非线性问题,Newton-Raphson方法能将非线性方程线性化来求解非线性问题。文中有限元分析方法基于以下假设:

1)柔性接头弹性件不可压,且在形变前为各向同性;

2)弹性件橡胶材料满足ODGEN二阶本构方程的描述;

3)计算中忽略动态因数导致的惯性力影响,摆动的响应过程作准静态处理。

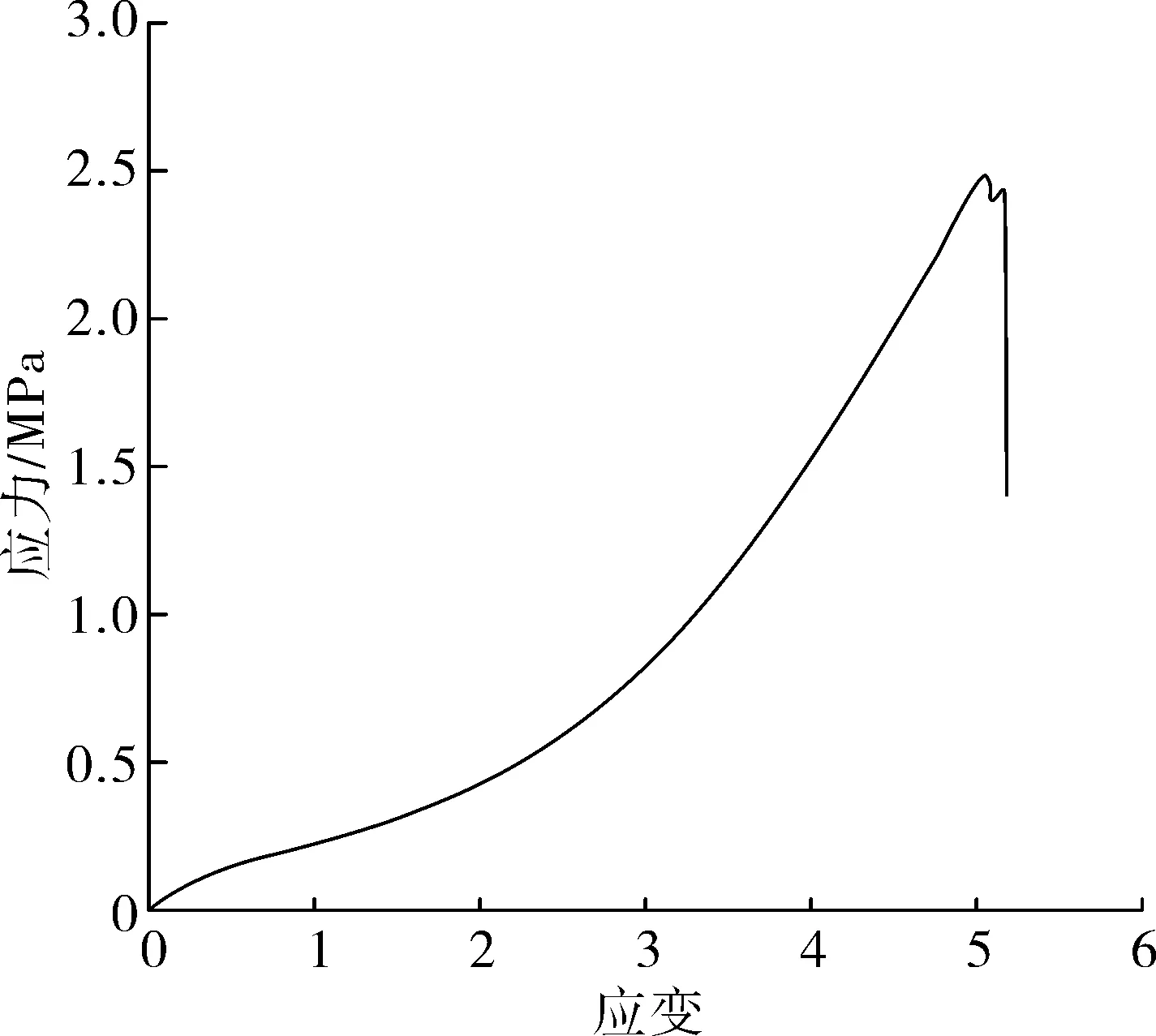
图5 四板剪切试样应力应变曲线(35HA)

2.1 柔性接头结构完整性

当容压P=12.3 MPa、摆角θ=7°时弹性件应力、应变分布云图分别如图6(a)、图6(b)所示。由应力分布可知,弹性件主要区域应力在5MPa以下,图中灰色区域部分所示有应力集中现象存在,应力集中处数值为40 MPa以上。弹性件主要区域应变保持在1.2以下,远小于试验测得拉伸、剪切极限应变量。弹性件出现较高的应力区域集中在柔性接头0°和180°摆动平面。实际试验过程中,对应柔性接头模型0°和180°截面,考虑在交变应力的作用下,柔性接头应力集中区域提前发生疲劳,呈现褶皱性失效,如图6(c)、图6(d)所示,计算与试验结果趋势吻合。

增强件主要区域应力在400 MPa以下,如图7所示,远低于材料屈服强度863 MPa。综上所述,排除疲劳破坏的影响,该柔性接头弹性件和金属件能在高压载荷工况下保持结构完整性。

2.2 弹性摆动力矩

在球坐标系下,以摆心为圆心,取某球面上弹性件单元,研究该单元上的应力对摆心的力矩效果。如图8所示。所选单元坐标(Ri、θi、φi),单元剖面应力为σ11、τ12、τ13,C3D8H单元其他5个单元面上的应力对于所取球面为内力,因此不作考虑。其中σ11经过摆心,不产生力矩;τ12、τ13为转动过程中的纬向剪应力和经向剪应力,他们是弹性件沿摆心转动时剪切变形直接引起的。因此,将球面上所有单元的τ12、τ13对摆心取矩并积分求和,即得接头转动所需的弹性力矩,计算公式为:

(2)

图7 增强件Von-mises应力

采用ABAQUS/Standard稳态求解器求解接头±7°摆角时弹性件剪切应力τ12、τ13分布,如图9、图10所示。纬向剪应力τ12最大值为1.3 MPa,远小于材料平板剪切强度2.5 MPa,而经向剪应力τ13除图中灰色区域有应力集中现象,其他大部分区域应力水平在极限剪切强度2.5 MPa以下,表明在该工况下接头能保持结构完整性。同时分析表明,柔性接头在有限偏转过程中,其经向剪应力τ13远大于纬向剪应力τ12,影响接头弹性力矩的主要是材料的剪切模量。

图8 接头应力分析示意

图9 弹性件纬向剪应力τ12

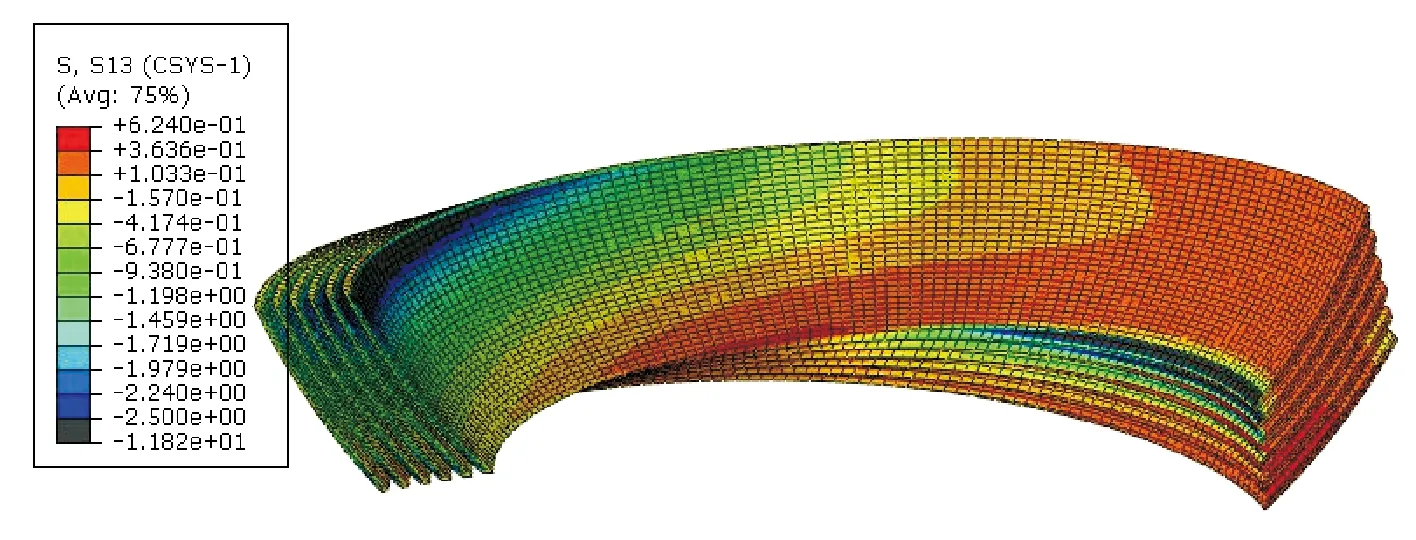
图10 弹性件经向剪应力τ13

对某批(共3只)柔性接头在压力为12.3 MPa下进行了低频3 Hz、±7°的正弦摆动。测量并记录了柔性接头摆角-力矩试验曲线,见图11。由图11可知,曲线呈回环状态,曲线包络面积代表着每个周期损耗的能量,曲线上下两部分有近似线性区域,说明柔性接头的力矩存在与摆角呈比例的弹性部分。

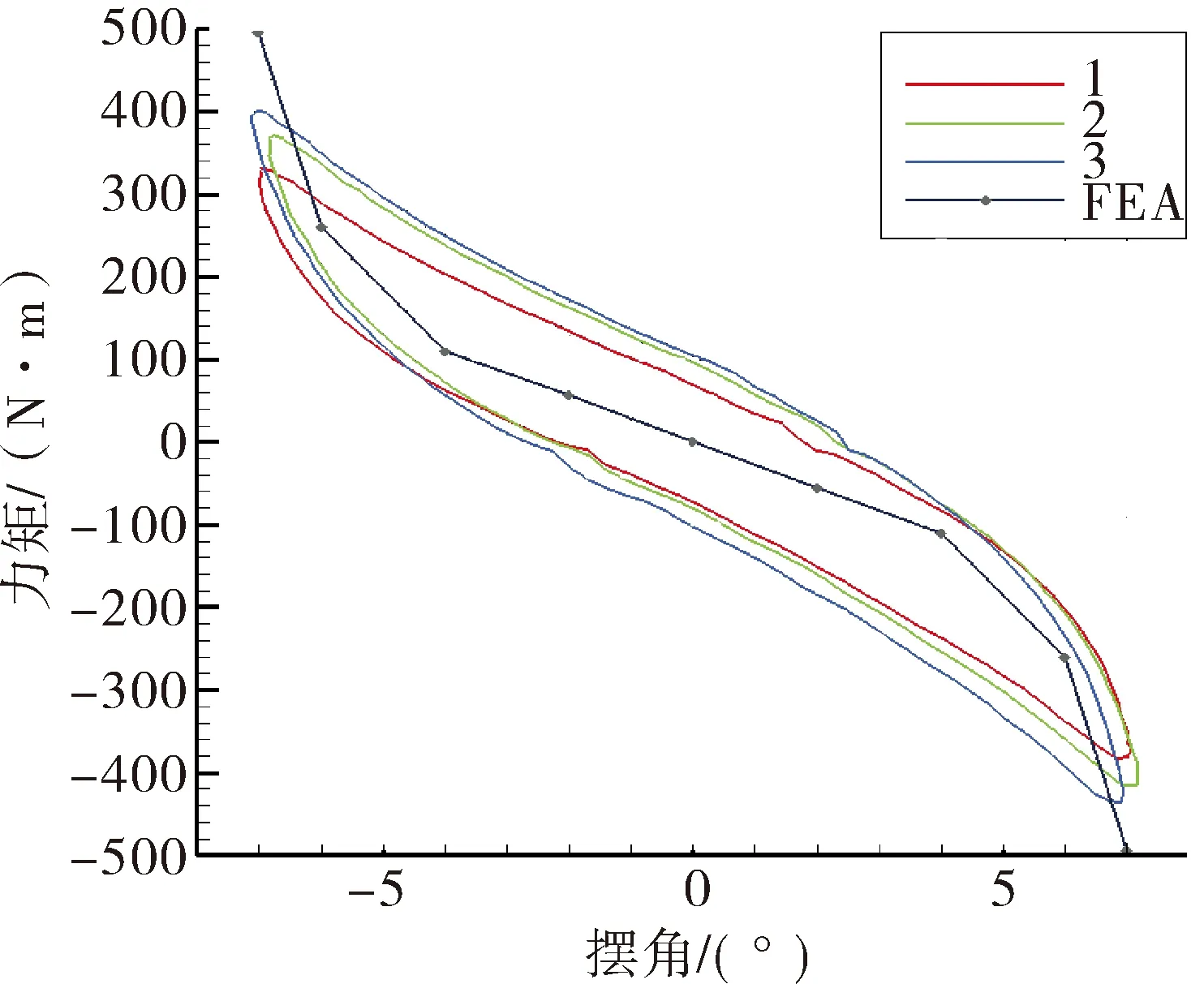
图11 1、 2、 3#接头摆动力矩试验曲线

通过稳态求解弹性件剪切应力τ12、τ13分布,根据式(2)对摆心积分求和可得接头摆动±7°区间力矩曲线如图11所示,最大力矩为±494 N·m,略大于高频摆动试验测试值368 N·m或-410 N·m。由于计算模型是理想状态,认为柔性接头的结构是完全对称的,因此计算曲线关于0°轴线严格对称,由图11可见,±6°范围内计算曲线完全落在试验曲线包络中,且趋势基本吻合,说明在该角度区域,ODGEN本构模型能较准确反应超弹性材料的力学性能,计算结果能比较准确的预示柔性接头的摆动力学性能。同时,稳态求解器过滤了高频响应下惯性力、摩擦等因数,这也是造成计算与试验结果差异的原因。

2.3 接头轴向刚度

柔性接头在高压载荷下的刚度直接影响喷管的摆心漂移,是影响喷管性能的重要指标。图12是不同压力载荷下前后法兰的轴向位移试验结果和数值分析结果对比。结果表明,柔性接头轴向压缩位移随压力的增加而增加,但上升趋势逐渐放缓。采用ODGEN二阶本构方程计算的结果在低压载荷区与试验结果较吻合,而在高压载荷区,数值分析结果略低于试验结果。试验中柔性接头在容压为12.3 MPa时的合成轴向位移约为1.35 mm,略高于计算结果1.05 mm。分析认为这种差异是由仿真过程中对柔性接头有限元模型施加了较多的固定约束，同时忽略了封头的弹性形变造成的。

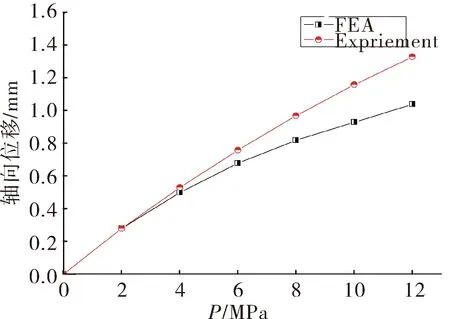
图12 不同压力载荷下轴向位移曲线

3 结论

使用单轴拉伸与简单剪切橡胶材料试验数据,获得了橡胶本构方程材料系数,建立了以柔性接头为研究对象的三维有限元模型,通过计算和试验对照,给出了柔性接头在高压载荷下工作的3个结论:

1)采用ODGEN的二阶本构方程进行有限元计算能有效的预示柔性接头在高压载荷条件的弹性力矩、轴向刚度、应力应变分布及失效模式等,为柔性喷管复杂工程问题的数值解法提供了参考;柔性接头轴向压缩位移随压力的增加而增加,但上升趋势逐渐放缓。计算的结果在低压载荷区与试验结果较吻合,而在高压载荷区,数值分析结果略低于试验结果。

2)弹性件出现较高的应力集中位于柔性接头0°和180°摆动平面,该区域是接头摆动过程中最先疲劳失效的区域,接头局部疲劳失效是后续重点研究方向。

3)驱动柔性接头转动的力主要是为了克服弹性件的剪切应力,其经向剪应力τ13远大于纬向剪应力τ12,影响接头弹性力矩的主要是材料的剪切模量。