多变量非高斯风压的高性能智能预测
2019-06-21李春祥涂伟平
李春祥, 涂伟平
(上海大学 土木工程系,上海 200444)
当今,世界范围内超高层建筑的高度和大跨桥梁的跨度已成为许多国家经济和技术实力的重要体现。我国在这方面已经处于世界领先地位。例如,已建成及在建的600 m以上超高层建筑有苏州中南中心、深圳平安国际金融中心、武汉绿地中心、上海中心大厦和天津高银117大厦,标志我国已处于千米高度级超高层建筑的发展初期。而将于2019年建成的沪通长江大桥为主跨1 092 m的钢桁梁斜拉桥结构,为目前世界上最大跨径的公铁两用斜拉桥。这些结构高柔/长柔、低频、低阻尼水平,对风荷载相当地敏感,在极端风作用下超高层建筑和特大跨桥梁会产生剧烈的风致振动。因此,在这两类重大工程的设计过程中,极端风荷载已经成为控制结构安全性和使用性的关键因素之一。极端风,包括台风(Typhoon)或飓风(Hurricane)、下击暴流和龙卷风,其破坏力巨大。
在台风等极端风作用下,大跨桥梁和超高层建筑会产生剧烈的抖振。为确保大跨桥梁和超高层建筑的正常运行以及在极端风事件下的安全,现在基本上都在这些结构(例如苏通大桥和上海中心大厦等)上安装了结构健康监测(Structural Health Monitoring,SHM)系统来是实时监测台风风速风向和结构的动力响应。尽管如此,布置用于实测此类工程风速风向的风速仪是相当少的,绝大多数位置处的风速需根据少数点的实测记录来进行条件模拟或预测获得,以建立全尺度的实测风荷载信息。因此,发展先进的工程结构风速智能预测方法至关重要。
智能预测试图通过构造自动学习系统来模拟未知系统。支持向量机(Support Vector Machine,SVM)就是拥有众多优势的其中一种。SVM工作流程:先将若干预定的模拟或实测或试验样本随机地分成训练集和测试集;接着,通过核函数把输入数据(训练数据)非线性映射到一个高维特征空间,在高维空间拟合出输入和输出变量间的一种线性关系即预测模型;再使用测试数据评估模型的预测精度。与人工神经网络(Artificial Neural Network,ANN)相比,SVM执行结构风险最小化,以广义风险或误差上界的最小化为目标;而ANN执行经验风险最小化,以在训练集上的预测误差最小化为目标。与ANN相比,SVM具有泛化能力强、学习数据少、全局优化等优点。随后的最小二乘支持向量机(Least Squares Support Vector Machine,LSSVM))是SVM的修改版[1]。LSSVM用误差的平方项代替不敏感损失函数,把不等式约束条件转变成等式约束条件,实现了快速训练的目标。因此,运用LSSVM的脉动风速预测得到了一些应用与发展[2-3]。当然,每种方法都有其局限性,LSSVM也不例外。LSSVM的主要缺点在于核函数和正则化参数的选择。当样本含有异构信息(例如间歇性)或呈多组分或数据在高维特征空间分布不平坦(例如非高斯过程)时,核函数的选择是决定性的。核函数选定后,正则化参数(控制偏移回归函数的数据点)和核函数参数(影响回归函数的平滑度)高度地影响SVM和LSSVM的预测精度。与正则化参数相比,核函数参数对预测结果的影响更大。因为核函数参数会影响特征空间的分区结果[4]。不幸的是,支持向量机理论没有提供选择正则化参数和核函数参数的方法。为提升LSSVM的预测精度,许多领域的研究都表明,将LSSVM与智能优化特别是混合智能优化融合是一个有效的途径。但这可能带来计算速度的下降。因为这时的计算速度不仅取决于核函数的形式(稀疏变化的核函数有助于提高迭代的收敛速度),而且取决于智能优化算法迭代的收敛速度。本文的研究目标是发展多变量非高斯风压的高性能智能预测算法。而对于非高斯风压,由于其三阶矩(偏度)不为零和(或)四阶矩(峰度)不为3,导致非高斯脉动风压时程具有极强的不对称性,因而数据在高维特征空间分布不平坦。因此,本文将LSSVM与混合智能优化融合来建立多变量非高斯风压的高性能智能预测算法。
1 LSSVM
LSSVM将最小二乘线性理论引入SVM中,取代SVM使用二次规划来解决函数估计问题,把SVM不等式约束变为等式约束,将求解二次规划问题转化为求解一组线性方程,大大提高了求解问题的收敛速度和精度。LSSVM基本原理为:首先,使用一个非线性映射φ(·),将样本从原空间映射到特征空间φ(xi),使在原空间中的非线性回归问题转变成在高维特征空间中的线性回归问题。接着,在特征空间φ(xi)中,构造出最优决策函数。最后,反映射到原空间,从而完成线性回归。
对一组给定的训练样本集:T={(xi,yi)|xi∈Rn,yi∈R,i=1,2,…,t} ,其中,xi为输入向量;yi为相应的目标输出。LSSVM的线性回归函数可表示为
y(x)=ωTφ(x)+b
(1)
式中:φ(·)为非线性变换映射函数;ω为权向量;b为偏置量。
基于结构风险最小化原则,LSSVM的目标函数可描述为
(2)
式中:γ为正则化参数,且γ>0;ξi为松弛因子。
引入Lagrange乘数法,得到
(3)
式中:αi为Lagrange乘子。
依次对ω,b,ξ,α求偏导并令其偏导数为0得
(4)
进一步得到关于α和b的矩阵方程
(5)
式中:Ω=φ(xi)Tφ(xj)=K(xi,xj),i,j=1,2,…,N;K(·)为核函数;I为单位矩阵。经过上述求解之后,可得到LSSVM解决非线性问题的回归函数
(6)
核函数K(·)直接影响LSSVM预测性能,常见的核函数有:线性核函数、多项式核函数、径向基核函数(Radial Basis Function,RBF)和Sigmoid核函数。其中RBF具有优点:① 结构形式简单,即使对于多变量输入也不增加太多复杂性;② 径向对称,光滑性好,任意阶导数均存在,解析性好;③ 泛化能力强,构造的SVM有较强非线性预测能力。鉴于此,本文选择RBF作为LSSVM核函数,其数学表达式为
(7)
式中:σ为核函数宽度。
2 多变量非高斯风压的高性能智能预测
LSSVM有两个待定参数,一个是正则化参数(γ),控制样本超出计算误差的惩罚程度,另一个是核函数参数(σ),控制函数回归误差,并且直接影响初始特征值和特征向量。优化LSSVM参数常见智能算法有蚁群算法(Ant Colony Optimization,ACO)和粒子群优化算法(Particle Swarm Optimization,PSO)。ACO[5]通过人工仿照蚁群在觅食途径上留下的“信息素”来获得食物的方法而找到所求问题的最优解。ACO通过空间参数化概率分布模型进行全局搜索而产生最优解[6],并不断更新产生的最优解,使得所求解始终保持在最优区域,增强了所求解的精确性。ACO的缺点是其求解过程较复杂,迭代时间长,并且在迭代过程中容易停滞;优点是鲁棒性较强,精于全局搜索,且能很好地与其它优化算法组合。PSO[7]通过人工模拟鸟群的觅食行为得到全局最优解,在每一次迭代完之后对整个群体的最优位置进行更新,是一种新型的群体智能式算法。PSO的优点是结构简单,迭代时间短;缺点是迭代次数较多,很难跳出局部最优的陷阱,这也限制了PSO的更广泛应用。通过上面分析知,ACO优点可以弥补PSO缺点,于是李春祥等[8]提出了混合蚁群和粒子群优化(ACO+PSO)方法。ACO+PSO算法不仅将ACO强大的全局搜索能力和PSO运算速度快的优点进行了结合,还解决了ACO迭代时间长和PSO容易陷入局部寻优的问题。ACO+PSO主要分为两个阶段:第一阶段,利用ACO在整个解空间内搜索寻优,找到最优解所在区域;第二阶段,将ACO得到的寻优结果初始化PSO的粒子位置,然后在局部解空间内进行搜索寻优,从而找到最优解的位置。那么,基于混合蚁群和粒子群优化LSSVM是否能高性能地预测多变量非高斯脉动风压?多变量是指作为输入风压点数为多个,即利用周边风压点的风压数据来预测未知点的风压。本文提出ACO+PSO-LSSVM多变量非高斯风压预测算法。最优解定义为:在解空间(σ,γ)内寻找最优参数组合(σbest,γbest)。将解空间内的任一位置向量定义为X=(σ,γ),采用样本均方差值f(X)作为优化目标函数
(8)
于是ACO+PSO-LSSVM多变量非高斯风压具体步骤可表示如下。
步骤1 将原始风压样本划分为训练集和预测集,并进行归一化处理
(9)
步骤2 初始化ACO各参数,在一定范围内随机产生核函数参数σ和正则化参数γ随的组合(σ,γ)作为整个解空间集合I,将蚂蚁随机放置在解空间I中。
步骤3 启动ACO,采用训练集对LSSVM进行训练学习,在训练中,第k只蚂蚁在t时刻从集合I中选择第j个参数组合(σ,γ)的概率为
(10)
随着迭代次数的增加,需要利用下式更新解空间中j处的信息素浓度
τj(t+m)=(1-ρ)τj(t)+Δτj(t)
(11)
式中:ρ(0<ρ<1)为信息素的残留度;m为每次迭代所需时间;其中
(12)

(13)
重复步骤3,将得到的(σ,γ)置于集合FACO内。
步骤4 初始化PSO各参数,把粒子群中各粒子随机放置在步骤3得到的寻优结果FACO集合中,启动PSO,对LSSVM进行训练,计算各粒子的均方差
(14)
通过均方差找到个体最优值pbest,经过迭代之后找到群体最优值gbest;迭代过程中粒子的速度更新公式为
(15)
位置更新公式
(16)
式中:c1,c2为加速度因子,其变化范围为[0,2],一般取2;r1,r2在区间[0,1]随机取值。
步骤5 比较各粒子的个体最优值pbest与群体最优值gbest,如果pbest>gbest,则将gbest更新为pbest;重复上述步骤,将满足寻优条件的结果作为最优参数(σ,γ)输出;否则返回步骤3。
图1给出了ACO+PSO-LSSVM多变量非高斯风压预测算法的流程。

图1 ACO+PSO-LSSVM多变量非高斯风压预测流程
Fig.1 Flowchart of ACO+PSO-LSSVM for multivariate non-Gaussian wind pressure
3 基于实测多变量非高斯风压的数值验证
对一栋办公楼楼顶砌筑的矩形建筑结构进行现场实测[9],其实测点布置如图2所示。图2中,沿AB墙面竖直方向等间距布置5个测点,编号为1#~5#;沿AD墙面竖直方向等间距布置5个测点,编号为6#~10#,其中AD为迎风面,AB为背风面。本次现场实测在2012-11-23,记录了300 min的风压时程数据,采样频率为20 Hz。本文取实测风压的前80 s(1 600个数据点)作为原始样本,如图3所示。将AB墙面1#、2#、3#测点风压数据作为训练集,2#、3#、4#测点风压数据作为测试集;AD墙面6#、7#、8#测点风压数据作为训练集,7#、8#、9#测点风压数据作为测试集。

3.1 预测方案
本文对空间点风压数据进行内插训练学习,得到基于智能算法优化LSSVM的风压预测模型,然后对其它高度的测点风压数据进行预测。所谓内插训练学习,即是对于在同一竖直面上的3个测点风压时程,利用上下两个测点风压时程作为输入样本,中间测点风压时程作为输出样本,对LSSVM模型进行训练学习,构造确定的输入输出关系,建立LSSVM风压预测模型;接着,将预测模型应用到其它高度进行预测,预测方案如图4所示。为了探究训练样本数目对模型预测性能的影响,本文设置两种内插训练方案。
(1) 3/4条训练(方案一):即将上中下3个测点的风压时程数据按照3∶1的比例划分,利用风压时程的3/4作为训练集,对模型进行训练,建立预测模型,并预测其他测点,最后与实测值比较进行验证。具体为:对于AB墙面,利用1#测点、2#测点和3#测点的前60 s(1 200个数据点)作为训练集进行内插训练学习,后20 s(400个数据点)作为测试集对预测结果进行验证。为验证算法在不同高度的有效性和稳定性,在此以测点2#和测点4#处的风压时程作为输入,测点3#处的风压时程作为输出,进行数值验证分析;对于AD墙面:同AB墙面类似,利用6#、7#和8#测点建模,预测8#测点处的风压。
(2) 整条训练(方案二):即利用上中下3个测点的风压数据的整条时程作为训练集,对模型进行训练,建立预测模型,并预测其他测点,最后与实测值比较进行验证。具体为对于AB墙面:将1#、3#测点处整条数据80 s(1 600个数据点)作为输入,2#测点处80 s(1 600个数据点)作为输出,对各个预测模型进行内插训练学习,建立预测模型,对其他空间点风压进行预测。为了验证预测模型的预测效果,将2#、4#测点作为输入样本,预测出3#测点处的风压时程,并与实测值进行比较;对于AD墙面:将6#、8#测点处整条数据80 s(1 600个数据点)作为输入,7#测点处80 s(1 600个数据点)作为输出,对各个预测模型进行内插训练学习,建立预测模型,对其他空间点风压进行预测。为了验证预测模型的预测效果,将7#、9#测点作为输入样本,预测出8#测点处的风压时程,并与实测值进行比较。
3.2 LSSVM参数的混合智能优化
对LSSVM参数σ和γ的范围设置为:令σ∈[10-1,102],γ∈[10-1,103];表1给出了ACO和PSO的参数选取。

表1 ACO和PSO模型相关参数选取
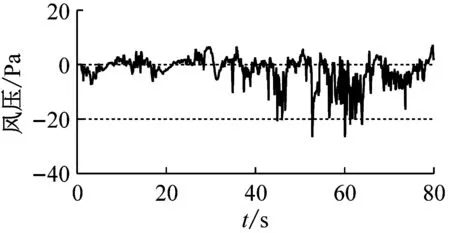
(a) 1#测点
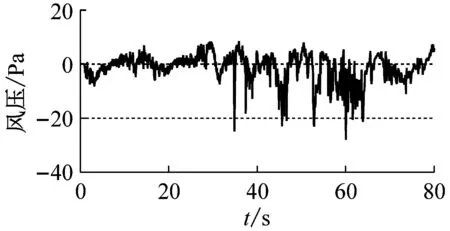
(b) 2#测点
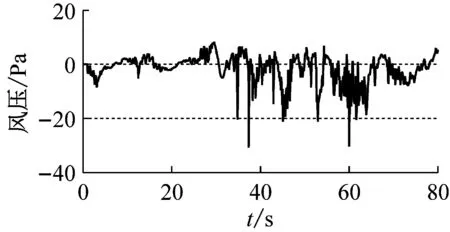
(c) 3#测点

(d) 4#测点
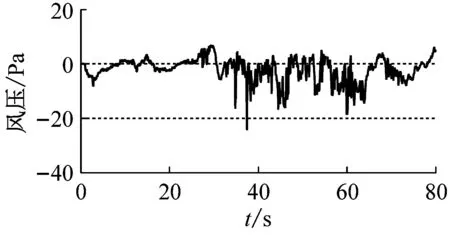
(e) 5#测点
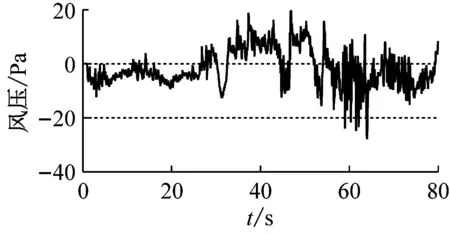
(f) 6#测点

(g) 7#测点
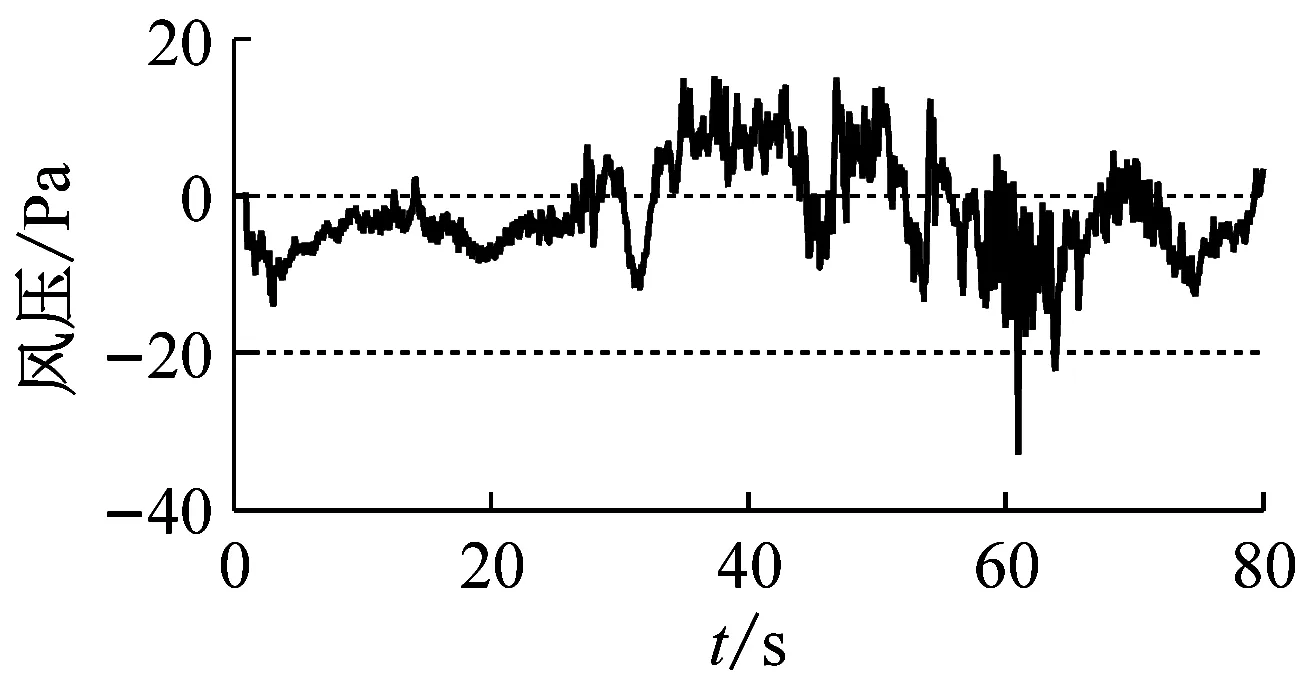
(h) 8#测点
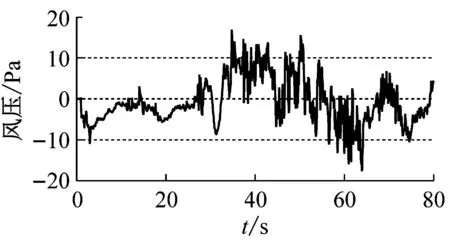
(i) 9#测点

(j) 10#测点
图3 原始风压时程图
Fig.3 Time history of initial wind pressures

图4 多变量非高斯风压预测方案 (方案一和方案二)
Fig.4 Prediction schemes for multivariate non-Gaussian wind pressure (schemes 1 and 2)
3.3 方案一的预测结果及分析
图5是3#和8#测点处在三种预测模型下的预测风压与实测风压时程图比较。从图5可知,三种预测模型的风压预测值跟实测值都比较吻合,在风压脉动性强的极值处,ACO+PSO-LSSVM的预测值较ACO-LSSVM和PSO-LSSVM的预测值更加接近实测值,因此,ACO+PSO-LSSVM对脉动风压尤其是具有极值点的不规则风压有着更好的预测效果;图6和图7分别为2个测点处预测风压与实测风压的功率谱密度函数、自相关函数对比,从图6和图7可知,相比于ACO-LSSVM和PSO-LSSVM,ACO+PSO-LSSVM的曲线更加接近实测数据,进一步验证所提预测模型的有效性和优越性;表2给出了2个测点的峰度和偏度对比,也可进一步验证所提预测模型的有效性和优越性。
为了评级模型的预测性能,分别利用平均绝对误差(MAE)、均方根误差(RMSE)及相关系数(R)来评价预测的有效性。表3给出了三种模型的预测性能指标对比。从表3可知,对于同一测点比较ACO-LSSVM和PSO-LSSVM,ACO+PSO-LSSVM的MAE、RMSE要更加接近于零,而R则更大,也可证明ACO+PSO-LSSVM的预测性能最佳。图8是空间点预测情况下三种模式的迭代次数对比图。从图8可知,PSO-LSSVM的迭代次数(约10次)和ACO+PSO-LSSVM的迭代次数(约15次)要低于ACO-LSSVM的迭代次数(约30次);表4给出了三种预测模型的训练集和测试集的MAE、RMSE和R的对比,以及最优参数和耗时的比较。从表4可知,PSO-LSSVM的训练时间最短ACO-LSSVM的耗时最长ACO+PSO-LSSVM的时间居中,因此,综合以上分析可得出:同时考虑预测精度和训练时间,ACO+PSO-LSSVM预测模型比ACO-LSSVM和PSO-LSSVM预测模型性能更佳。验证了所提出的基于混合蚁群和粒子群优化LSSVM算法在空间点风压预测中的优越性。

(a) 3#测点处预测风压和实测风压比较
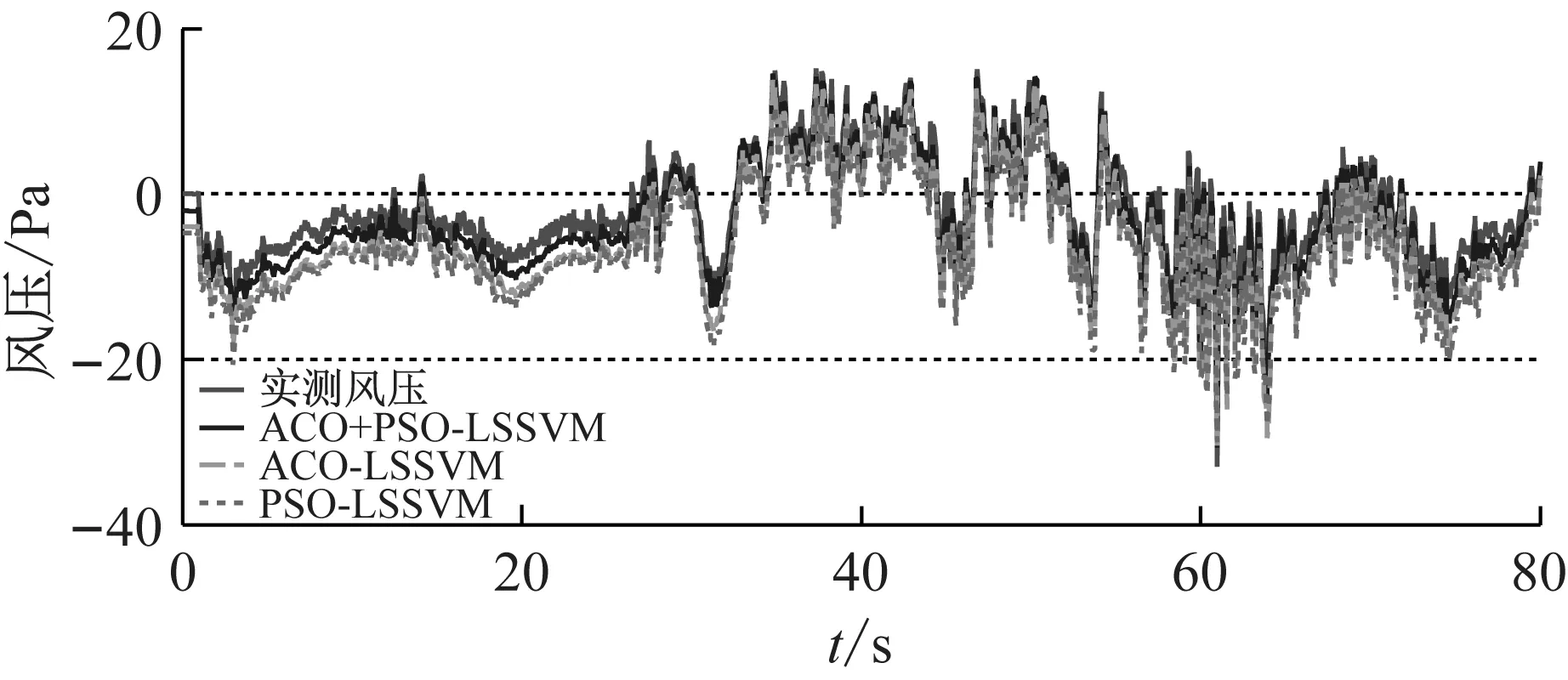
(b) 8#测点处预测风压和实测风压比较
图5 三种预测模型的风压时程(方案一)
Fig.5 Wind pressure time history using three kinds of prediction models (scheme1)

(a) 3#测点处预测风压和实测风压的功率谱密度函数比较
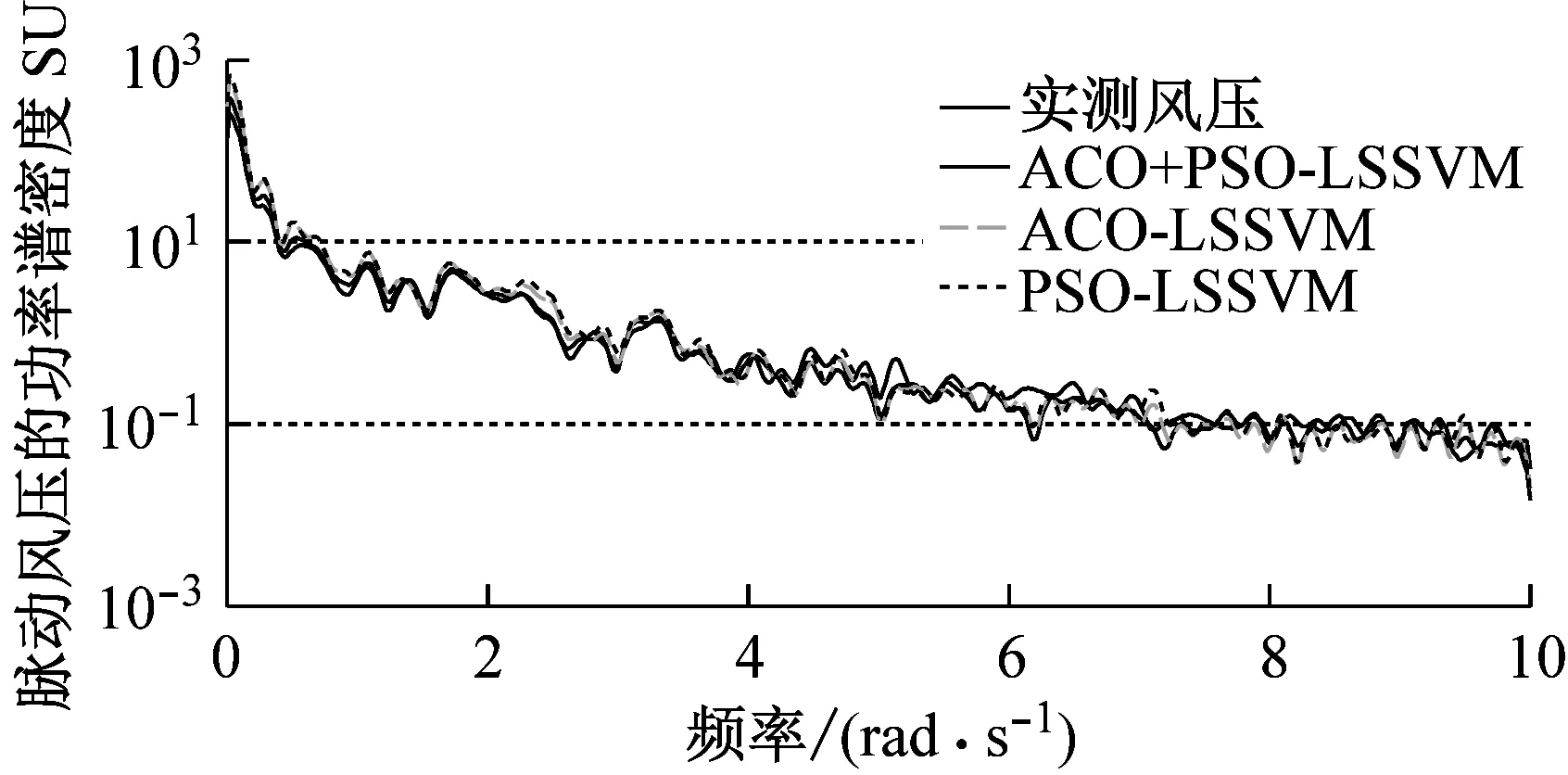
(b) 8#测点处预测风压和实测风压的功率谱密度函数比较
图6 三种预测模型的风压功率谱(方案一)
Fig.6 Wind pressure PSP using three kinds of prediction models (scheme1)
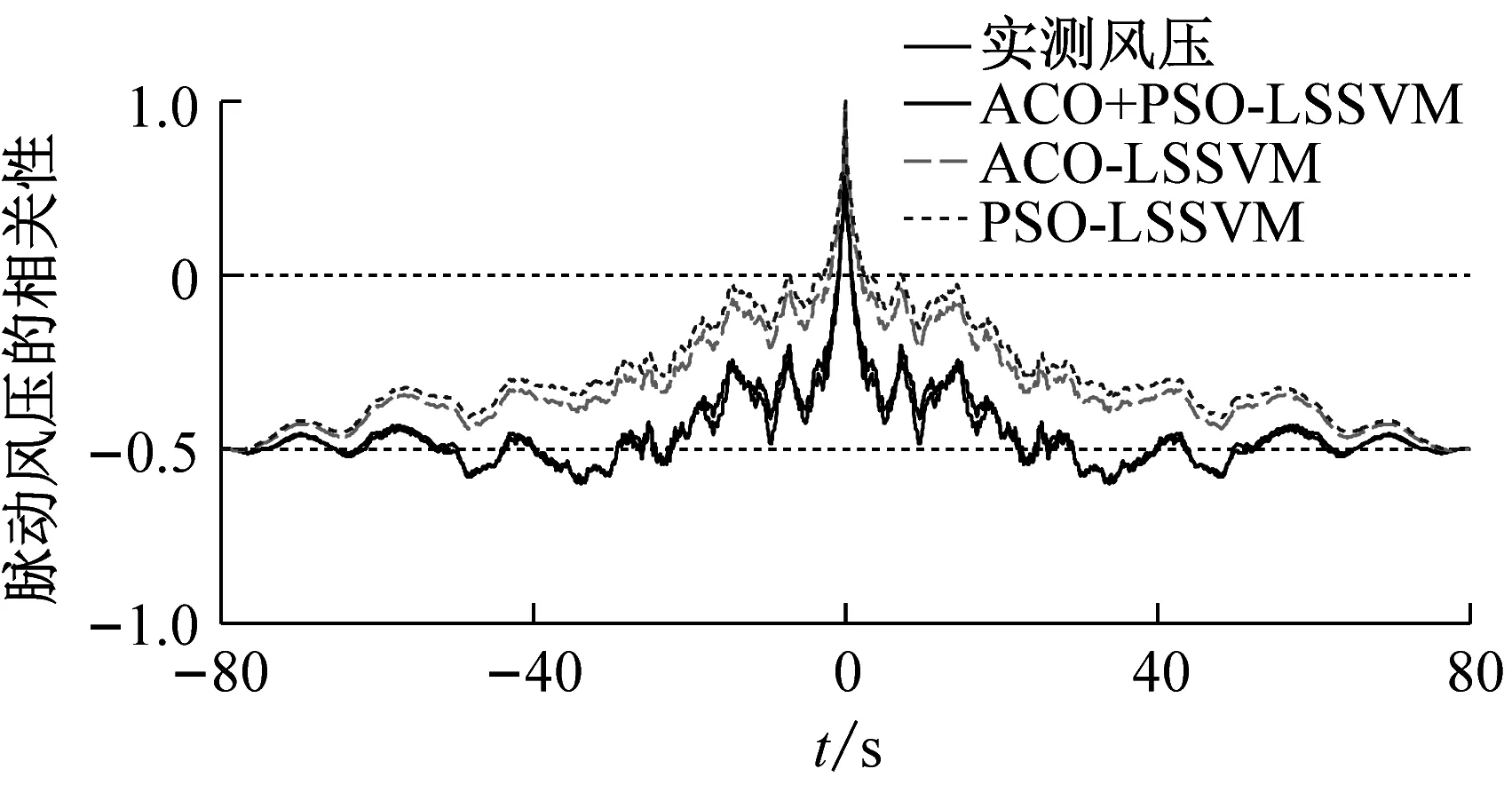
(a) 3#测点处预测风压和实测风压的自相关函数比较
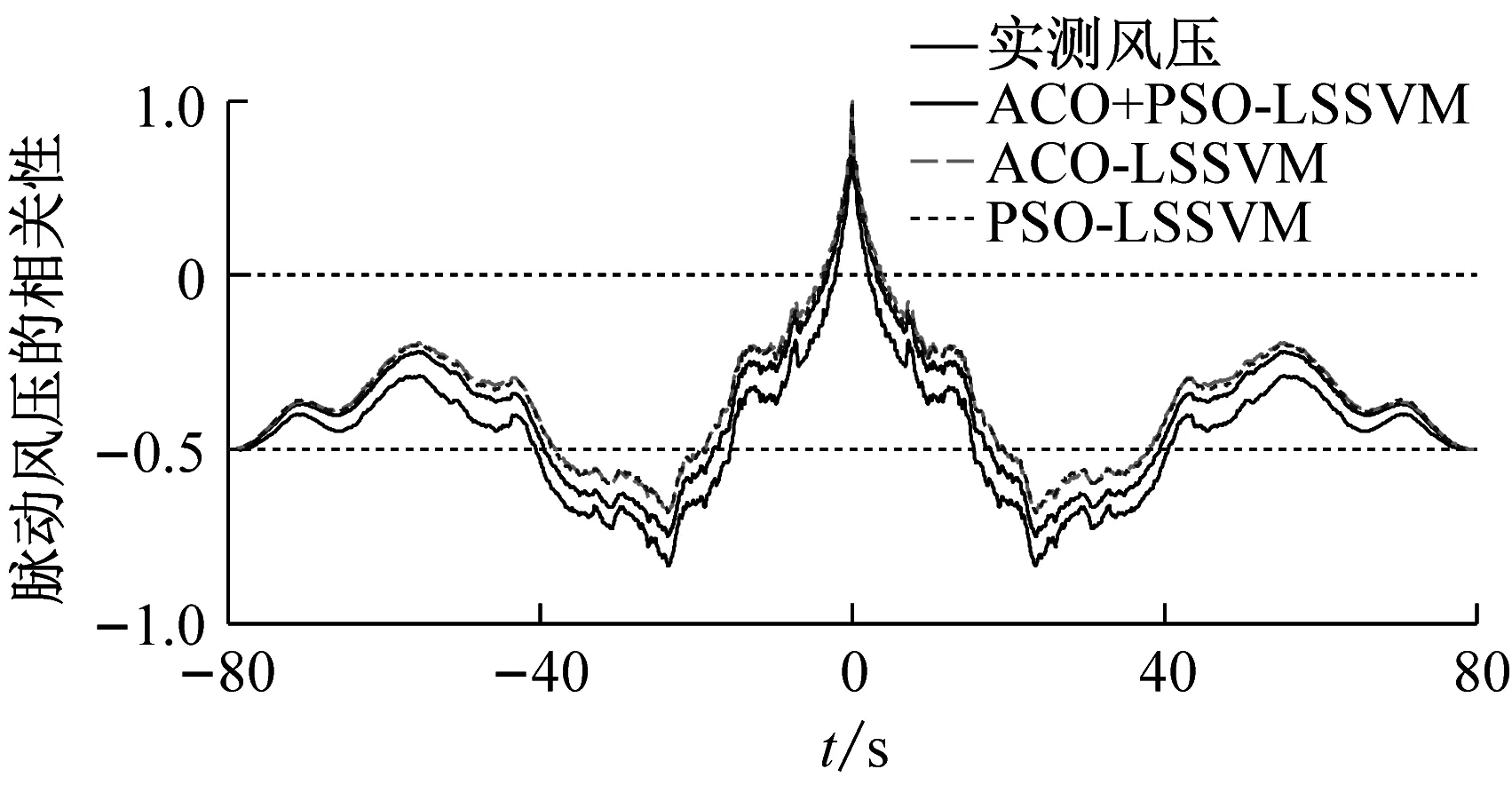
(b) 8#测点处预测风压和实测风压的自相关函数比较
图7 三种预测模型的风压自相关函数(方案一)
Fig.7 Wind pressure autocorrelation functions using three kinds of prediction models (scheme1)
表2 三种模型预测风压的峰度和偏度(方案一)
Tab.2 SK and K using three kinds of prediction models (scheme1)

预测模型3#8#SKKSKKACO-LSSVM-1.814.39-0.363.08PSO-LSSVM-1.054.010.222.86ACO+PSO-LSSVM-1.606.420.413.05注:SK=E(X-μ)3σ3,K=E(X-μ)4σ4,当偏度SK>0时,风压时程样本分布曲线为正偏态曲线,当偏度SK<0时,分布曲线为负偏态曲线;当峰度K>3时,称为平阔峰曲线,其尾部较高斯分布薄;当峰度K<3时,称为尖峭峰曲线,其尾部较高斯分布厚

图8 三种模型的收敛速度对比(方案一)
Fig.8 Rate of convergence for three kinds of prediction models (scheme1)
表3 三种模型的预测性能指标(方案一)
Tab.3 Prediction performance using three kinds of prediction models (scheme1)

预测模型3#8#MAERMSERMAERMSERACO-LSSVM3.684.000.922.462.730.92PSO-LSSVM4.464.750.893.343.630.89ACO+PSO-LSSVM1.832.060.970.971.370.97注:平均误差:MAE=1N∑Nn=1yn-y^n;均方根误差:RMSE=1N∑Nn=1(yn-y^n)2;相关系数:R=∑Ni=1yn·y^n∑Ni=1y2n∑Ni=1y^2n;yn为目标值(原始样本数据),y^n为预测值,N为预测样本数
3.4 方案二的预测结果及分析
图9为训练样本为整条时程数据时,3#和8#测点处整条风压时程图在三种模型下的预测风压和实测风压对比。从图9可知,三种模型的预测风压跟实测风压的值都比较接近,整体趋势也很吻合,且ACO+PSO-LSSVM的预测值相较于ACO-LSSVM和PSO-LSSVM更加吻合实测值,与方案一类似,在风压脉动性较强的极值处,这种优越性体现的较为明显,但是效果相比于方案一已经不是非常明显。因为最小二乘支持向量机在解决小样本的问题上更有优势,因此,当增加训练样本数目时,三个预测模型的预测效果区别已经不是那么明显了。

表4 三种模型的最优参数、耗时和预测性能指标(方案一)
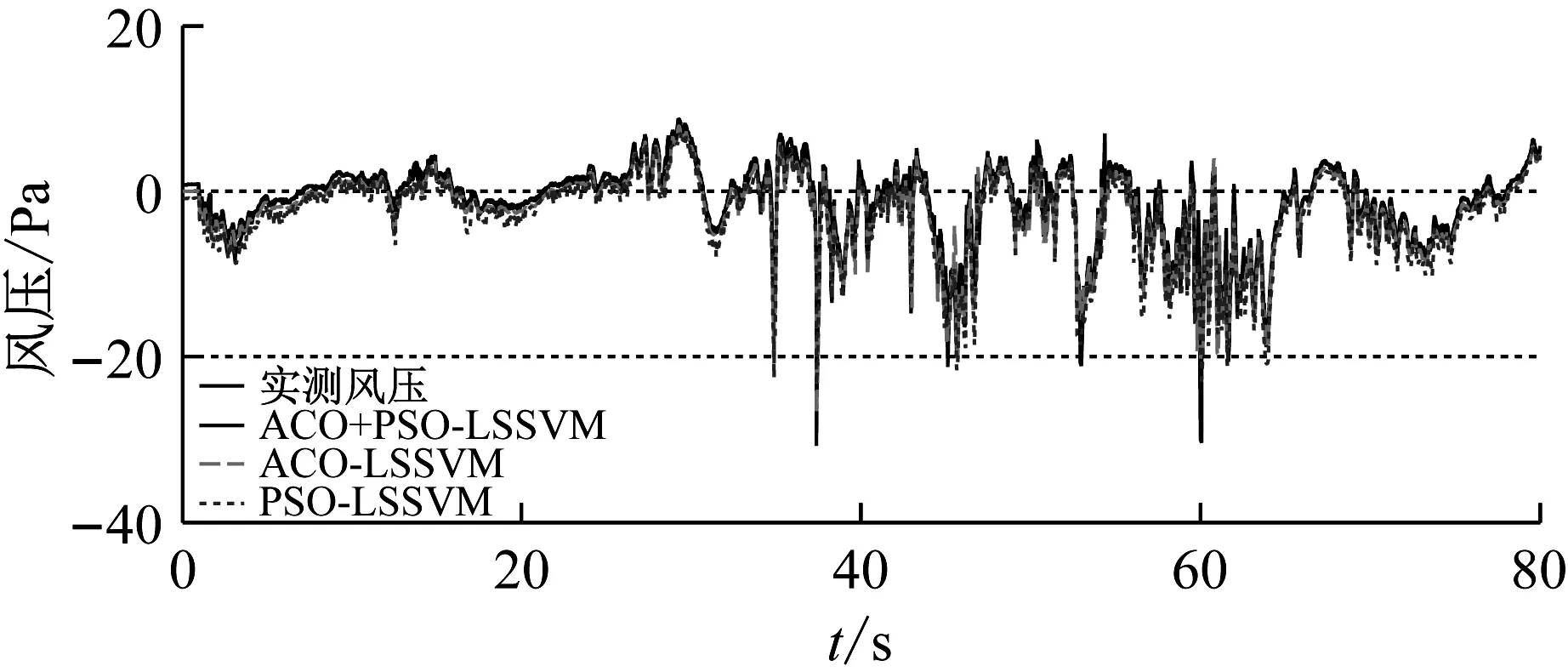
(a) 3#测点处预测风压和实测风压比较
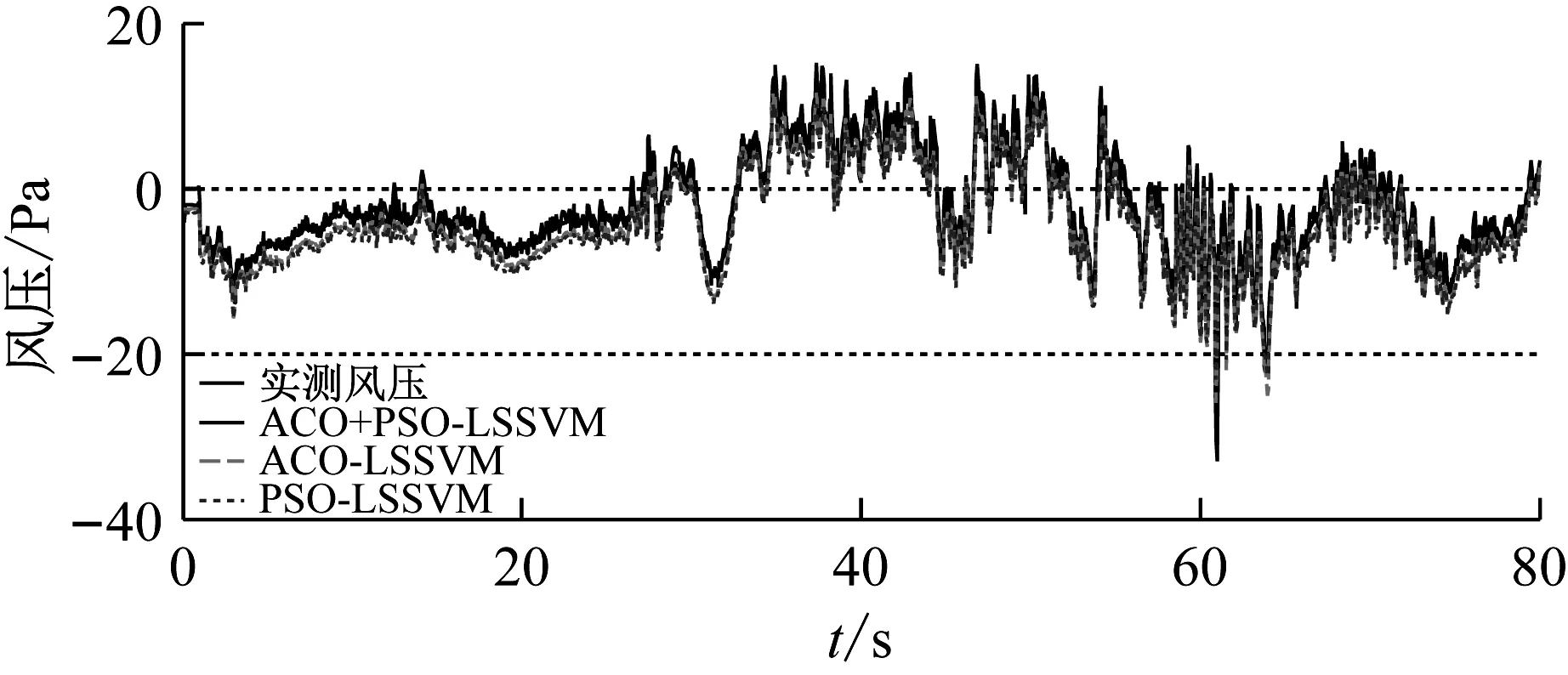
(b) 8#测点处预测风压和实测风压比较
图9 三种预测模型的风压时程(方案二)
Fig.9 Wind pressure time history using three kinds of prediction models (scheme2)
图10和图11分别为三种模型的预测风压和实测风压的功率谱、自相关函数对比,从图10和图11可知,两个曲线的吻合度也很高,且ACO+PSO-LSSVM的预测风压曲线更加接近实测风压;表5给出了三种模型的峰度和偏度对比。从表5可知,3#、8#测点实测风压偏度SK均不为0,3#测点的脉动风压为负偏,8#测点脉动风压为正偏,峰度K均大于3,呈现出明显的非高斯特性,亦可看出与实测风压的接近程度。表6是两个测点在三种预测模型下的MAE、RMSE和R的比较。从表6可知,ACO+PSO-LSSVM较ACO-LSSVM和PSO-LSSVM的MAE和RMSE要小,而R更大。因此,当训练样本为整条数据的时候,三种模型对空间点风压样本的预测效果都很好,且ACO+PSO-LSSVM预测模型的性能最优,但是其优越性已经没有那么显著。
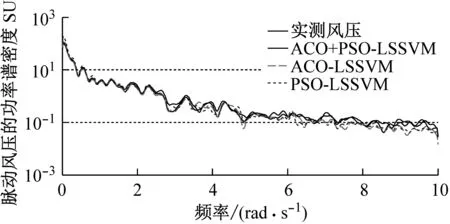
(a) 3#测点处预测风压和实测风压的功率谱密度函数比较

(b) 8#测点处预测风压和实测风压的功率谱密度函数比较
图10 三种预测模型的风压功率谱(方案二)
Fig.10 Wind pressure PSP using three kinds of prediction models (scheme2)
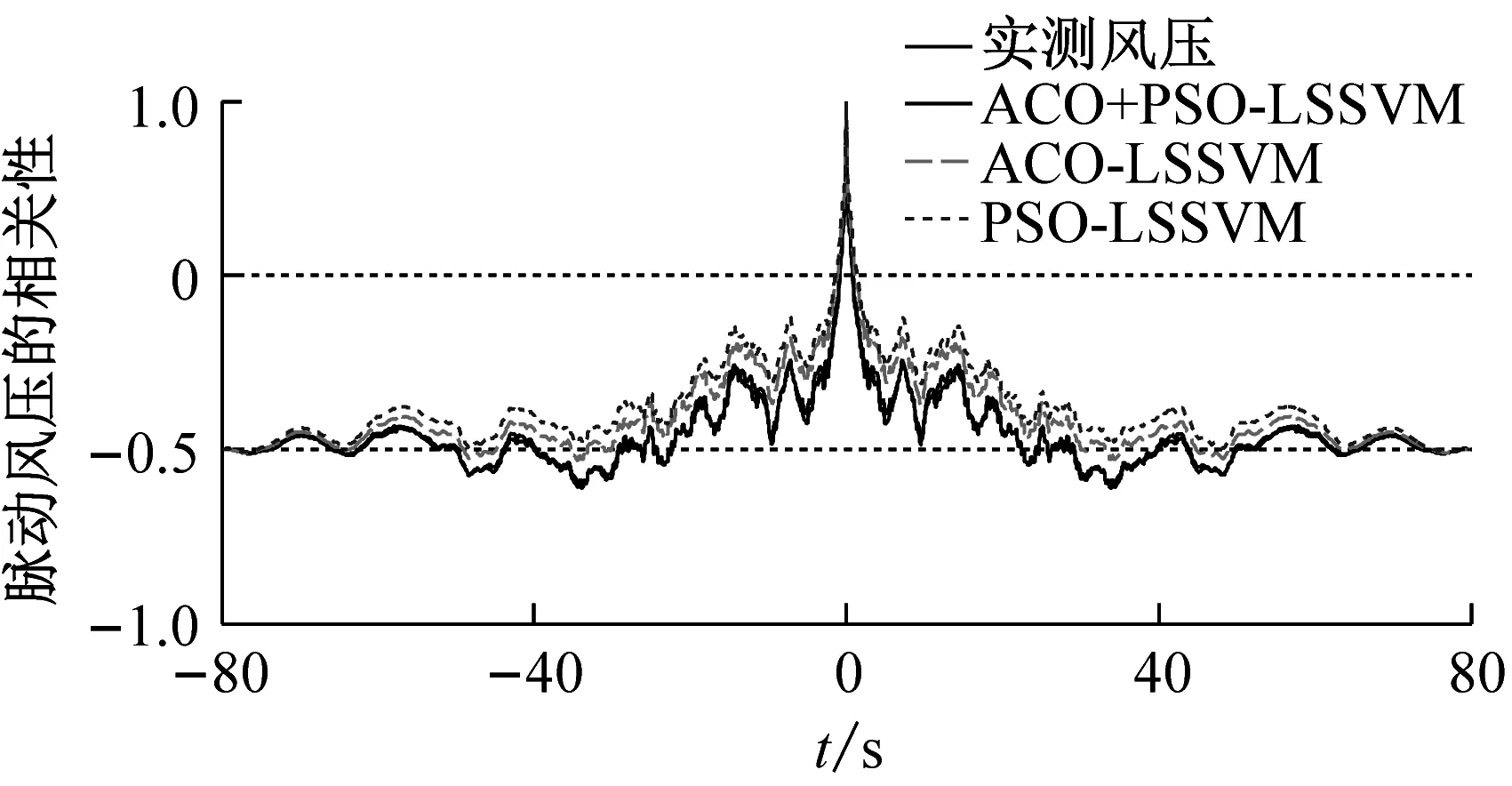
(a) 3#测点处预测风压和实测风压的自相关函数比较

(b) 8#测点处预测风压和实测风压的自相关函数比较
图11 三种预测模型的风压自相关函数(方案二)
Fig.11 Wind pressure autocorrelation functions using three kinds of prediction models (scheme2)
表5 三种模型预测风压的峰度和偏度(方案二)
Tab.5 SK and K using three kinds of prediction models (scheme2)

预测模型3#8#SKKSKK实测风压-1.406.130.243.52ACO+LSSVM-1.214.910.273.03PSO+LSSVM-1.164.470.332.79ACO+PSO-LSSVM-1.345.850.383.51
表6 三种模型的预测性能指标(方案二)
Tab.6 Prediction performance using three kinds of prediction models (scheme2)

预测模型3#8#MAERMSERMAERMSERACO-LSSVM1.141.720.952.152.460.94PSO-LSSVM1.551.900.942.612.890.92ACO+PSO-LSSVM0.711.070.981.071.360.96
4 方案一和方案二的预测性能
为了更直观的比较三种预测模型在训练样本数目不同情况下的预测性能,表7和表8分别给出了2个测点处整条样本数据训练和3/4条样本数据训练时三种模型的预测性能指标对比,从表7和表8可知,对于同一测点,当增大训练样本数目的时候,ACO-LSSVM和PSO-LSSVM的预测性能评价指标都有不同程度的提高,ACO+PSO-LSSVM的评价指标基本维持在同一水平;相较于8#测点,3#测点的预测性能评价指标提高的更为明显。因此,由以上分析可知,当训练样本有限时,使用方案一中的ACO+PSO-LSSVM预测模型对风压进行预测具有更优越的预测性能,更强的鲁棒性;当增加训练样本数目时,方案二中三种预测模型的预测性能都有不同程度的改善,且训练样本数目越大,模型预测性能越好,随着训练样本的逐渐增大,三种预测模型之间的预测性能差异在逐渐减小,也即ACO+PSO-LSSVM对于小样本的风压预测更能体现出其优越性。
5 结 论
提出ACO+PSO-LSSVM多变量非高斯风压预测算法。使用现场实测多变量非高斯风压数据,并通过比较ACO-LSSVM和PSO-LSSVM)结果,证实了ACO+PSO-LSSVM是一种多变量非高斯风压高性能预测算法。同时,本文给出了三种预测模型的两种预测方案(方案一、方案二)。当训练样本有限时,使用ACO+PSO-LSSVM的方案一对风压进行预测有更优越的预测性能,鲁棒性更强。当增加训练样本数时,三种预测模型中方案二的预测性能都有不同程度改善。而且,随着训练样本的逐渐增大,三种预测模型之间性能差异逐渐减小,因此ACO+PSO-LSSVM对于小样本风压预测更具优势。

表7 3#测点处在不同训练样本下的预测性能评价指标
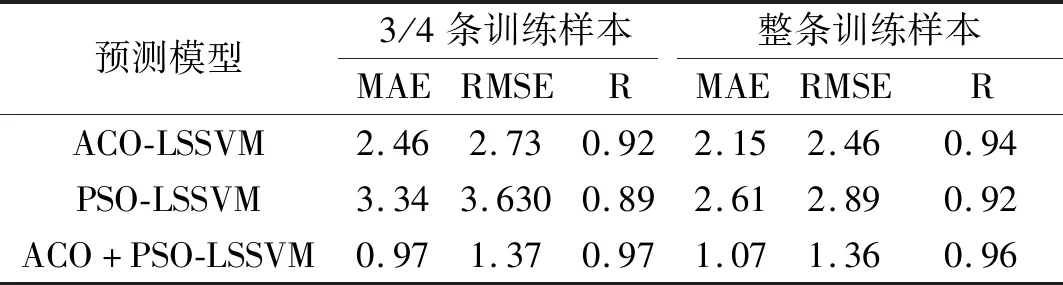
表8 8#测点处在不同训练样本下的预测性能评价指标
