基于Lorenz系统Lyapunov指数的管道超声导波检测

温宇立， 武 静， 林 荣， 马宏伟,3

(1. 广东海洋大学 机械与动力工程学院，广东 湛江 524088；2.东莞理工学院 建筑工程系，广东 东莞 523808；3.暨南大学 力学与建筑工程学院，广州 510632)

随着社会对能源需求的急速加剧，作为主要运输油气资源的管道运输发展步伐不断加快。国家统计局数据显示，2004年至2015年上半年，我国油气管道总里程累计增长206.3%，增长幅度巨大。由于管道运输的众多优点，已成为继铁路运输、航空运输、公路运输、水路运输之后的第五大运输方式，属于城市生命线之一。然而，在管道长期服役过程中，不可避免的出现缺陷、损伤。若不能及时的发现并修复缺陷管道，后果不堪设想。因此，对管道进行安全检测意义重大。超声导波检测技术是近年来发展较快的一种无损检测技术[1-2]，相比于传统检测技术，超声导波检测技术具有检测方便、检测速度快、单次检测距离长、检测范围广等优点[3-4]。

由于导波的频散、多模态、衰减特性，在实际的长距离检测中，若缺陷较小，则被测量的缺陷回波信号微弱，而传感器本底噪声、功率放大器的固有噪声以及外界的干扰噪声等往往远高于有用信号的幅值，因此反射回波信号必将呈现出强噪声下弱信号的特征，这将严重的影响检测信号的识别、定位，从而影响检测结果的准确性。现时，国内外学者对于超声导波检测的主要研究方向分别为：超声导波在不同波导介质中的传播特性[5-6]、激发与接收导波的仪器[7-8]以及信号处理。信号处理作为超声导波检测的最后一个阶段，其对检测结果起着至关重要的作用，而现时的信号处理方法在导波信号处理上均有一定的局限性，如二维傅里叶变换[9]在特定情况下会出现假频现象；小波变换[10]要选择十分合适的母小波较为困难；时间反转聚焦法[11]在聚焦过程中容易出现其他的杂波，影响检测结果。由于混沌理论对混沌模型的初始条件具有极端敏感性而对噪声具有一定免疫能力，因此基于混沌系统突变效应的检测方法给信号处理领域提供了一个新方向。混沌振子检测简单正、余弦信号的有效性已被验证[12-13]，但用于识别超声导波信号的研究较少，且研究的混沌模型主要为Duffing方程等非自治混沌系统[14-16]。相比于二维的Duffing方程，Lorenz方程的非线性特性以及动力学行为更加丰富，在弱信号处理领域更具优势。因此，本文将以Lorenz方程为基础，通过非共振周期信号的参数激励实现受控Lorenz系统的构建，并用于识别数值模拟和试验所得的管道超声导波信号，以此验证方法的有效性。

1 混沌模型及参数选择

1.1 基于混沌理论的弱导波信号识别原理

混沌现象是非线性系统所特有的一种运动方式，表现为确定性系统在确定的初始状态下出现类似随机的非周期运动，混沌振子的动力学行为对运动的初始条件十分敏感，且对噪声免疫。超声导波信号是由多个单音频正弦信号加窗调制而形成的带宽信号，信号主瓣高，旁瓣迅速衰减，能量主要集中在中心频率附近。基于混沌振子的导波信号检测则是利用了混沌系统的动力学行为对系统参数及其敏感的这一特点，基本思想是通过利用非线性系统中的时间项对导波信号的中心频率敏感而对噪声信号不敏感的特性构建特定的混沌系统，使得系统处于平衡的临界状态，将待测信号作为混沌系统的一个微小扰动引入系统，若待测信号为导波信号，则系统会发生非平衡相变，动力学行为状态发生改变；若待测信号为噪声信号，则系统状态不发生改变，最后根据待测信号中有无导波信号及待测信号的时间段来进行损伤的识别。

1.2 Lorenz系统的建立

Lorenz方程是描述空气流体运动的模型，是历史上研究最早的混沌模型之一，也是全局动力学行为已得到深入分析和严格证明的经典自治系统，其系统方程为

(1)

标准的洛伦兹方程中各系统的参数为σ=10，r=28,b=8/3，此时对应的系统处于混沌状态。混沌系统检测弱信号的基础是混沌的控制，利用周期信号非共振激励进行混沌控制近年来应用较好的自治系统开环控制方法，通过利用与检测信号同频的周期信号进行参数激励使得Lorenz系统处于系统状态改变的临界点。因此当检测信号输入时，即改变参数激励幅值，Lorenz系统状态会发生根本性的改变，从而检测出待测目标信号。非共振周期信号参数激励后的Lorenz系统表达式为

(2)

1.3 Lorenz系统参数的选择

在研究Lorenz系统混沌特性时，最常用的方法是固定σ=10、b=10/3，将r作为变量研究。根据大量的仿真研究结果表明，r=4较为适合超声导波信号检测。由混沌系统检测弱信号的原理可知，参数激励的频率需要与检测目标信号频率一致。而在管道超声导波检测中，检测信号多用Hanning窗调制的10周期，中心频率70 kHz的单音频正弦信号，其表达式为

(3)

式中:n为周期数，fc为信号的中心频率。因此周期信号参数激励的频率为ω=0.439 823 rad/μs，激发信号的时域波形和频谱分析,如图1所示。

(a) 时域波形

(b) 频谱

(4)

(5)

(6)

实际计算时，取d=1，根据式(4)、式(5)、式(6)计算式(2)表示的Lorenz检测系统在有无导波信号输入时对应的四个Lyapunov指数L1、L2、L3、L4随强迫激励幅值k的变化。

如图2(a)、图2(b)所示，在未输入导波信号时，随着k的增大，Lorenz系统的y，z，t方向对应的Lyapunov指数均为非正数，而x方向对应的Lyapunov指数逐渐增大，最终大于0。输入导波信号时，系统各方向对应的Lyapunov指数变化的趋势与未输入导波信号时类似。因此，为了选取适合导波信号检测的阈值，只需要对比有无标准导波信号输入时Lorenz系统x方向对应的Lyapunov指数即可。从图2(c)可知，k在区间[0.475 7,0.990 3]以及[1.144 7,1.144 9]时，未输入导波信号时系统为周期状态，输入导波信号系统转变为混沌状态。为了提高系统的灵敏度，从中选取输入导波信号前后使得系统Lyapunov指数变化最大的策动力幅值作为Lorenz系统的检测阈值，因此系统的参数激励幅值设为k=0.986 6。

2 数值模拟与试验信号识别

2.1 数值模拟信号识别

利用ANSYS有限元软件模拟超声导波在无损、单裂纹、双裂纹钢质管道中的传播。管道的有限元模型参数如下：管道总长6 m，直径50.8 mm，壁厚1 mm，选用shell181单元进行有限元分析，传播总时间t=2.5 ms。大量的试验和Murigendrappa等[18]的研究证实，工业中管道的损伤多为环向裂纹，因此设置本文的管道缺陷类型为环向裂纹，单裂纹损伤位于管道左端3 m处、双裂纹损伤位于管道左端2 m和4 m处且损伤大小相同。检测信号由管道左端面激发，接受信号位置距管道左端50 mm，并通过平均信号减少弯曲波的影响。检测示意图及缺陷截面形状如图3所示，并考虑表1所示的4种工况。

(a) 无导波信号输入

(b) 标准导波信号输入

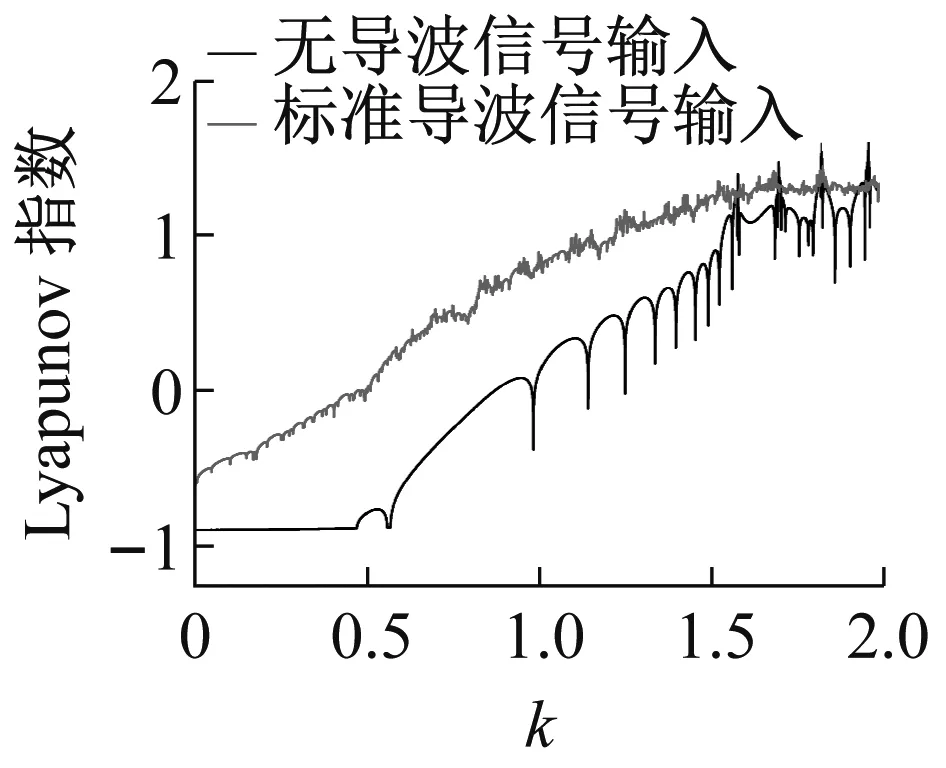
(c) 有无导波信号输入对比

图2 Lorenz系统Lyapunov指数随k变化

Fig.2 The Lyapunov exponents of Lorenz system change withk

通过提取接收点的位移时程曲线可以得到导波信号的传播过程，此外为了模拟实际检测中外部噪声的影响，向数值模拟得到的管道超声导波信号中添加噪声水平为0.02的高斯白噪声，其结果如图4所示。

表1 缺陷设置

(a) 工况1

(b) 工况2

(c) 工况3

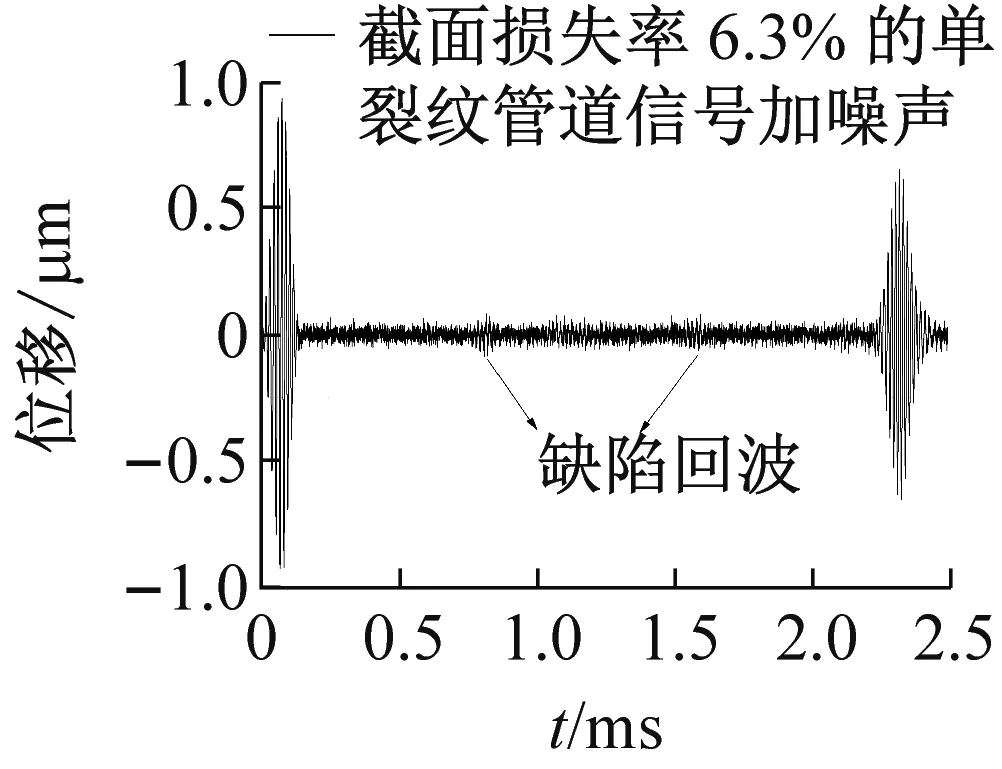
(d) 工况4

图4 数值模拟信号

Fig.4 The simulation signals

从图4可知，在单裂纹以及双裂纹缺陷的截面损失率较小时，缺陷回波信号极容易被噪声所淹没，只有当缺陷的截面损失率高于9.4%时，才能直接观测到缺陷回波。此外在双裂纹管道中，相比于单裂纹管道，模态转换现象更加严重，使得缺陷回波波形愈加复杂。这些都不利于缺陷的识别，容易造成误判或者漏判的结果，影响检测的准确性。通过计算，单裂纹管道缺陷回波的时刻位于t1=1.132 ms，双裂纹管道的缺陷回波时刻约在t2=0.755 ms，t3=1.51 ms。为了验证Lorenz系统Lyapunov指数识别管道中弱导波信号的可行性，从4种工况的回波信号中截取0.60～0.95 ms，0.95～1.35 ms，1.35～1.7 ms输入Lorenz检测系统中，观察对应的Lorenz系统Lyapunov指数的响应状态。

如图5所示，当工况1表示的无损管道待测信号输入后，由于管道中不存在损伤，输入信号为纯噪声信号，因此Lorenz检测系统的Lyapunov指数正负值并没有发生改变，与无信号输入时的响应相同，说明Lorenz检测系统具有较好的噪声免疫能力，将工况2、工况3、工况4对应的损伤管道的三段信号输入后，含有缺陷回波的信号输入后系统的Lyapunov指数从负值转为正值，说明系统从周期状态转变为混沌状态；而不含缺陷回波信号输入后，系统的Lyapunov指数依然为负值，系统运动状态仍为周期状态，成功的识别出单裂纹与双裂纹。数值模拟的识别结果有效地证明了Lorenz系统Lyapunov指数识别管道中弱超声导波的可行性。

(a) 工况1

(b) 工况2

(c) 工况3

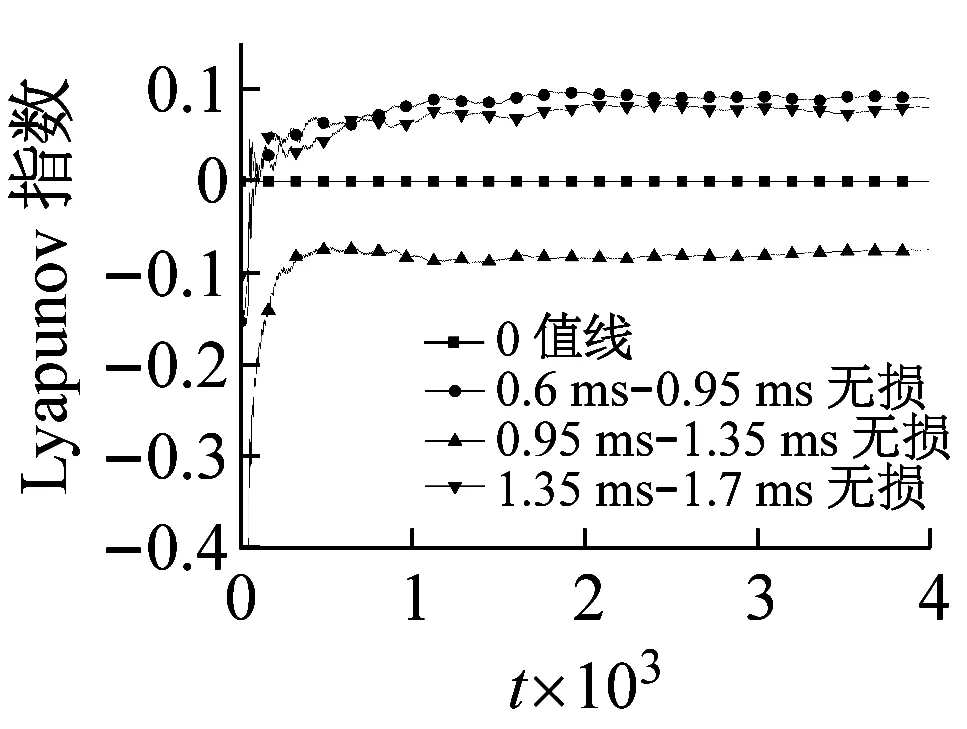
(d) 工况4

图5 不同数值信号的Lyapunov指数

Fig.5 The Lyapunov exponent with simulated signals inputting

2.2 试验研究

数值模拟算例从数值理论上验证了该方法的可行性，为了证明该方法同样能很好的应用于实际检测中，选用与数值模拟算例尺寸相同的管道进行试验研究，利用锯弓在管道上制造人工缺陷进行试验，同时为了验证数值模拟得到的结果，缺陷位置、大小、类型的设置参考表1中4种工况的设置。试验中采用PZT5材料作为超声导波的激发和接收传感器，为了激发时能够产生对称的L(0,2)模态导波，按照管道截面尺寸加工压电环，利用压电环激发导波，加工的压电陶瓷片尺寸为15.4 mm×3.2 mm×0.9 mm，将一组16片均布管道一周的压电片并联作为接收传感器，可有效的减少接收信号中的弯曲模态。试验设备如图6所示。波形信号发生器将编辑好的导波信号通过功率放大器放大后施加于管道端面的压电环，利用逆压电效应在管道中产生纵向超声导波，最后通过压电片接收信号，并利用示波器采集和保存信号，示波器的采集数据的时间步长为0.04 μs。

图6 试验设备

图7为表1所示的4种工况下接收到的试验信号，从中可以看出，在损伤较小时，在外界噪声的影响下，使得回波信号与无损管道的结果相类似，难以直观地判别出管道的损伤情况，容易造成误判或漏判。当缺陷的截面损失率逐渐增大至9.4%时，才能观察到缺陷回波的轮廓。然而在实际检测中来自环境、仪器等外部的噪声必然会远远高于试验进行时的噪声，因此在实际应用时超声导波检测的识别精度会比9.4%更差。

(a) 工况1

(b) 工况2

(c) 工况3

(d) 工况4

图7 试验信号

Fig.7 The experimental signals

为了提高超声导波检测的灵敏度以及检测范围，使得检测能够应用的更加广泛，分别截取入射波和端面回波之间0.60～0.95 ms，0.95～1.35 ms，1.35～1.7 ms等三个时间段作为待测信号，输入到Lorenz检测系统中，其Lyapunov指数的响应结果如图8所示。

(a) 工况1

(b) 工况2

(c) 工况3

(d) 工况4

图8 不同试验信号的Lyapnov指数

Fig.8 The Lyapunov exponent with experimental signals inputting

当将无损管道的3个待测段信号输入后，由于信号中不含缺陷回波，因此Lorenz系统响应的Lyapunov指数均为负值，系统仍为周期状态，与无信号输入时相同。而当工况2、工况3表示的单裂纹管道信号输入后，对应着损伤的0.95～1.35 ms段信号输入后系统的Lyapunov指数从负值转变为正值，而另外两段无缺陷回波的纯噪声输入后系统的Lyapunov指数正负值没有发生改变且最终收敛数值差异很小，从而判断出0.95～1.35 ms信号中存在着损伤。同理，工况4所表示的双裂纹管道信号输入后，对应着损伤的0.60～0.95 ms、1.35～1.7 ms信号使得Lorenz系统Lyapunov指数正负值发生改变，且最终收敛数值接近，表明系统由周期状态转变为混沌状态，表明0.60～0.95 ms以及1.35～1.7 ms信号中含有缺陷回波。此外，通过对比发生损伤处的信号输入后Lorenz系统Lyapunov指数的响应数值，可以发现，缺陷截面损伤率与响应的Lyapunov指数数值呈一个正相关的关系，这说明Lyapunov指数的收敛值能够一定程度反映缺陷回波的幅值以及缺陷的大小。

3 缺陷定位

上述的数值模拟与实验研究证明了基于Lorenz系统Lyapunov指数识别管道超声导波信号的可行性以及有效性，但在实际的管道损伤检测中，除了检测有无损伤，损伤定位更是无损检测中极为重要的一部分。

参考文献[19]的研究证明了不同长度的导波信号均可以相轨迹发生改变，说明混沌系统对导波信号的响应与导波信号的完整性关联不大。因此，基于Lyapunov指数定量识别混沌系统状态的特点，利用二分法对导波信号进行分解，逐步定位出缺陷回波信号的发生时间，在一定精度下实现缺陷的定位。具体步骤如下：

步骤1 首先将接收到的回波信号进行幅值归一化；

步骤2 通过软件计算波速，然后去除回波信号的入射波以及端面反射波，得到待检测信号；

步骤3 利用二分法将待测信号分解为两段等长的A信号与B信号；

步骤4 将A信号输入混沌检测系统当中，取系统计算的Lyapunov指数的收敛值作为系统的状态判据，若A段信号的Lyapunov指数从负值变为正值时，则判定该段信号中含有缺陷回波信号，对A段信号继续分解定位；若Lyapunov指数不变则说明其中无导波信号，转而检测B段信号。

步骤5 将B段信号输入混沌检测系统中，若Lyapunov指数正负值改变则对B段信号继续分解，若不变则说明其中无导波信号；

步骤6 重复步骤3、4、5，对导致系统Lyapunov指数正负值改变的信号段进行逐级的等长度分解，最后通过波速计算距离，直到获得满足检测精度的定位结果。

以试验研究中工况4表示的双裂纹管道为例，选取0.4～1.8 ms部分作为待检测信号，以±0.5 m为损伤定位的精度，对缺陷回波信号进行时域定位，其应用二分法分解过程中对应的Lyapunov指数,如表2所示。直接将0.4～1.8 ms部分信号输入后，系统Lyapunov指数响应变为正值，说明该段信号中存在缺陷回波；因此对该段检测信号进行第一次对等二分，分为0.4～1.1 ms以及1.1～1.8 ms两部分，分别将两段信号输入Lorenz系统中，两段信号对应的Lyapunov指数正负值也发生了改变，因此证明了这两段信号中分别存在着缺陷回波。对这两段信号分别再次对等二分，得到0.4～0.75 ms、0.75～1.1 ms、1.1～1.45 ms、1.45～1.8 ms四段信号，输入Lorenz检测系统后仅有0.75～1.1 ms、1.45～1.8 ms两部分信号使得Lyapunov指数转变为正值，但通过计算，定位的精度不符合要求，因此对0.75～1.1 ms、1.45～1.8 ms再进行一次对等二分，最终确定缺陷回波位于0.75～0.925 ms、1.45～1.625 ms中，分别对应管道1.975～2.436 m、3.819～4.280 m，与损伤设置的情况相符，满足精度要求，实现了缺陷的简单定位。

表2 工况4的损伤定位

4 结 论

混沌控制是混沌系统检测弱信号的基础，基于周期信号非共振激励能够实现自治系统混沌控制的特质，本文提出了一种基于Lorenz系统Lyapunov指数的弱超声导波检测方法。利用Lyapunov指数定量识别混沌系统状态的优势，分别对比加入导波信号前后Lorenz系统Lyapunov指数随周期信号激励幅值变化的规律，选择合适的Lorenz检测系统激励幅值。通过数值模拟与试验研究，利用该Lorenz检测系统对在管道中传播的弱超声导波信号进行识别，从而实现损伤检测，并得到以下结论：

(1) 识别结果表明了Lorenz检测系统具有一定的噪声免疫能力，具有应用在强噪声环境下弱超声导波检测的潜力。

(2) 在有限元与实验结果中，当缺陷截面损失率为9.4%以上时，才能观察到缺陷回波的波形，而通过Lorenz系统Lyapunov指数可识别到6.3%甚至更小的缺陷。

(3) 在一定的范围内，Lorenz系统Lyapunov指数与缺陷的截面损失率成正相关关系，能够通过Lyapunov指数简单判断下损伤。

综上所示，利用本文的识别方法能够判断管道有无损伤、损伤个数和损伤定位，实现了管道缺陷的识别；此外，该识别方法能够有效的免疫噪声，实现高噪环境下的损伤识别，提高了超声导波检测识别小损伤的精度，具有实际的工程应用价值。