快速加载下轴压比对RC梁柱节点抗震性能的影响

杨天戈， 范国玺, 王 也， 王德斌, 商怀帅

(1.中国海洋大学 工程学院,山东 青岛 266100;2.大连交通大学 土木与安全工程学院,辽宁 大连 116028;3.青岛理工大学 土木工程学院,山东 青岛 266033)

建筑物在其使用年限内，不仅承受设备、人群、土压力等静态荷载作用，经受风、雪、雨、日照等自然环境作用，而且可能遭受波浪、水流、地震、爆炸等动载作用。在上述作用中，地震作用是较常见的间接作用[1-3]。近年来地震频发，如我国的汶川地震(2008年5月12日)[4]、意大利的L’Aquila地震(2009年4月6日)[5]、土耳其的Van地震(2011年10月23日)[6]、意大利的Emilia region地震(2012年5月)[7]、厄瓜多尔的Muisne地震(2016年4月16日)[8]。历次地震，均造成了巨大的人员伤亡和财产损失，严重影响着人类生存的自然环境。此外，地震作用往往造成建筑物的严重破坏甚至倒塌，建筑物的安全性和可靠性不仅影响工农业生产，而且关系到人身安全[9-10]。因此，研究建筑物的抗震性能具有重要的意义。

地震作用下，梁柱节点由于其复杂的受力特征，往往先于其他部件出现损伤，随着地震的持续作用，损伤不断积累与发展，致使节点的抗震性能退化并最终失效，进而引发整体结构的破坏。国内外多次地震灾害表明，大量房屋建筑的破坏与倒塌是由梁柱节点破坏引起的[11-12]。另一方面，受黏性效应、裂缝演化和惯性效应物理机制的影响，混凝土材料具有率敏感性，受位错滑移-爬升机制(低加载速率)和绝热剪切带机制(高加载速率)的影响，钢筋亦具有率敏感性[13-14]。钢筋混凝土构件由混凝土和钢筋两种材料组成，上述材料的率敏感性必然对钢筋混凝土构件的动态力学性能产生极其重要的影响。已有研究表明，动态荷载作用下，荷载高频成分以及材料应变率效应，增大了构件的高频振动，致使钢筋混凝土构件的损伤程度、承载能力、刚度退化、耗能能力等均随加载速率的变化而变化[15-19]。

目前，有关梁柱节点抗震性能的研究多数为拟静力试验研究，钢筋混凝土梁柱节点动态试验研究相对较少。基于上述考虑，对四个梁柱节点组合体试件进行了快速加载试验，梁端加载速度均为40 mm/s，试件JM2-7、JM2-17、JM2-4、JM2-8的轴压比分别为0.05、0.10、0.15、0.25，以此研究较高应变率水平下轴压比对钢筋混凝土梁柱节点抗震性能的影响。

1 试验概况

1.1 试件制作

图1 梁柱节点配筋图

屈服强度/MPa极限强度/MPa直径/mm核心区箍筋4815578梁纵筋36854118柱纵筋34251222

1.2 加载设备及加载制度

采用电液伺服控制多通道协调加载系统对试件进行加载，该系统可控制三个方向作动器进行动静加载。柱顶采用吨位为200 T的作动器通过荷载控制对柱身施加固定轴压力，柱顶通过与加力架相连的钢支撑固定以保证节点组合体平面内外的稳定性，柱底安放球铰。两侧梁端作动器通过位移控制施加往复荷载，作动器与梁端通过连接件连接，可实现往复拉压，作动器吨位分别为30 T和50 T。

通过ABAQUS有限元分析软件，采用混凝土损伤塑性模型以及考虑强化效应的钢筋双折线模型，混凝土单元选用八节点六面体线性减缩积分单元C3D8R，钢筋单元选用三维二结点桁架单元T3D2，建立钢筋混凝土梁柱节点计算模型，对梁柱节点进行单调静态加载数值模拟。分析结果表明，梁端屈服位移约为10 mm。以此确定试验加载制度为：按照预定轴压比水平，于柱顶施加轴向压力，该轴向压力加载到最大值需20 s，试验过程中保持轴压力恒定不变，预压(消除变形误差等)60 s后，分别于两侧梁端部，按照位移控制反对称变幅往复加载，幅值5 mm，10 mm各循环一次，然后以10的倍数(20 mm，30 mm，…)进行加载，每个位移等级对应循环两次，直到试件承载力下降至最大承载力的85%以下或者发生最终破坏为止。梁端以40 mm/s的恒定速率连续加载。

1.3 测量方案

试验过程中，通过电液伺服控制多通道协调加载系统实时记录作动器的加载位移及施加荷载，通过imc64通道CRONOS PL-8数据采集设备实时测量钢筋应变及试件变形，通过数码相机实时记录裂缝发展过程。

2 混凝土抗剪计算模型

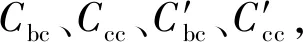
基于塑性下限理论，在经典桁架模型理论基础上发展起来的拉-压杆模型，可以通过分析结构的弹性主应力迹线，对应力紊乱区的节点核心区进行抗剪承载力的计算。然而，拉-压杆模型未能有效地体现节点核心区混凝土在拉、压复合作用下抗压强度的软化效应，且选择不同的荷载传递路径，会导致设计结果不唯一，因此，未能在设计应用中得到广泛地推广[21-22]。为此，Hwang等[23-24]提出了用于梁柱节点抗剪承载力计算的软化拉-压杆模型，该模型可综合考虑节点核心区的平衡条件、变形协调条件以及开裂混凝土的本构关系，能够较好地预测梁柱节点的抗剪承载力。

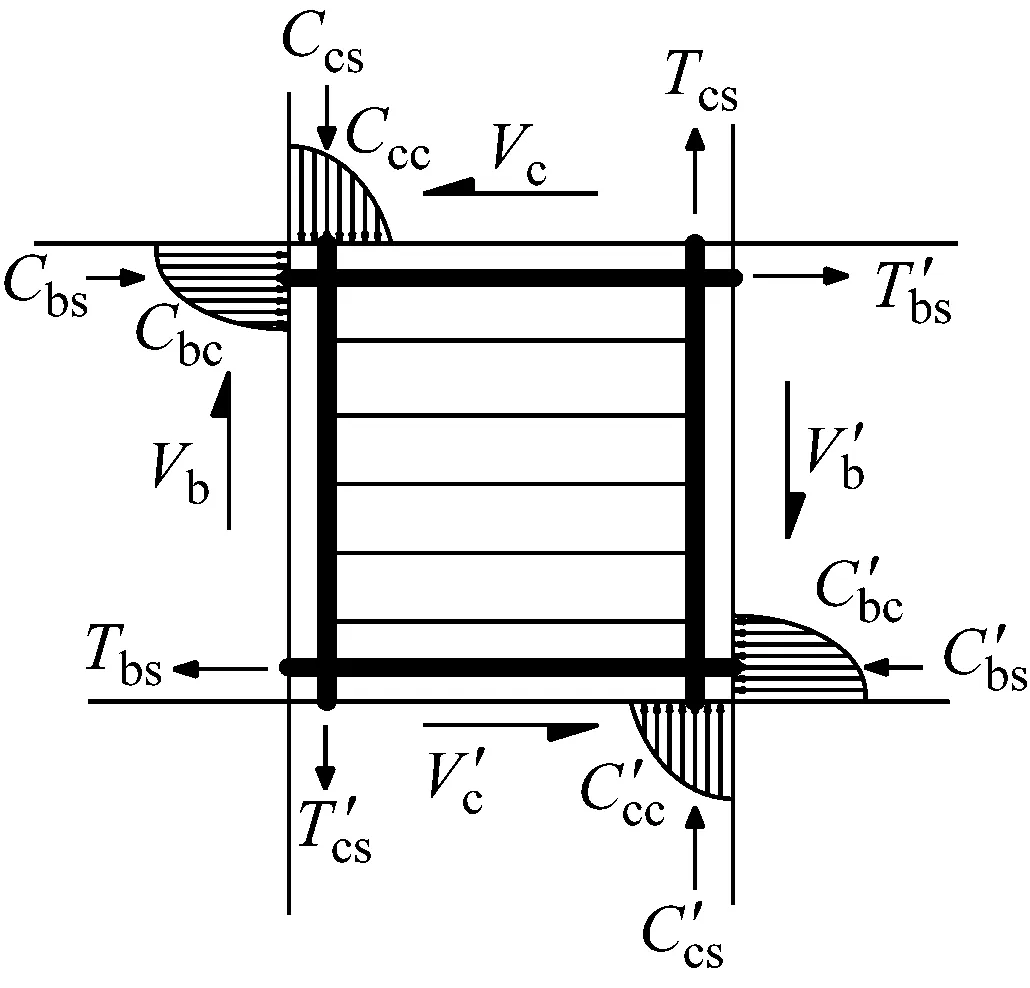
图2 梁柱中节点受力模型

如图3所示，软化拉-压杆模型中梁柱节点的抗剪机构由斜向机构、水平机构和竖向机构三部分组成。其中，斜向机构由混凝土对角斜压杆构成，如图3(a)所示；水平机构由1个水平拉杆(水平拉杆由节点水平箍筋组成)和2个混凝土平缓压杆构成，如图3(b)所示；竖向机构由1个竖直拉杆(竖直拉杆由节点内柱纵筋组成)和2个陡峭压杆构成，如图3(c)所示。

(a)

(b)

(c)

图3 节点抗剪机构

Fig.3 Joint shear-resisting mechanisms

根据改进的软化拉-压杆模型，混凝土软化系数ζ为[25]

(1)

(2)

式中，γh为为水平拉杆的拉力与节点水平剪力的比值，其计算公式为

(3)

斜压杆的倾角θ可以由水平和竖向两个方向上剪力的内力臂求得

(4)

(5)

(6)

假定钢筋的应力-应变本构关系满足理想的弹塑性模型，则水平拉杆的屈服荷载Fyh为

Fyh=AthEsεh

(7)

式中:Ath为水平拉杆的截面面积；Es为钢筋的弹性模量；εh为水平拉杆的应变。

斜压杆的有效截面面积Astr定义为

Astr=as×bs

(8)

式中:bs为斜压杆有效截面的宽度，可以取节点的有效宽度；as是斜压杆有效截面的高度，其计算公式如下所示

(9)

式中，ab和ac分别为梁截面、柱截面受压区的高度。

(10)

斜压杆的名义承载力Cd,n为

(11)

相应的节点水平抗剪承载力Vj为

Vj=φCd,ncosθ

(12)

式中，φ为承载力折减系数，通常取0.85[27]。

试验测得的节点组合体水平抗剪承载力记为实测值，运用软化拉-压杆模型计算得到的节点组合体水平抗剪承载力记为理论值。拟静态加载下，轴压比为0～0.25，上述公式的计算结果如表2所示。

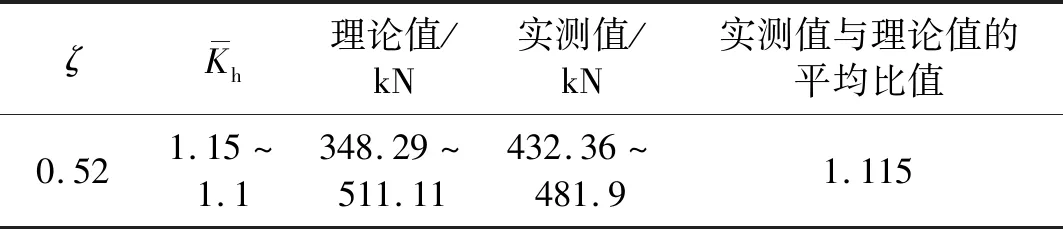
表2 计算结果

运用软化拉-压杆模型，可得轴压比为0～0.25时，斜压杆的极限承载力为897.41～1 376.81 kN，水平拉杆的极限承载力为280.17 kN。结合θ和γh的取值可知，水平拉杆屈服后，斜压杆仍能继续承载，水平拉杆破坏后，斜压杆混凝土才能被压碎，最终节点核心区发生斜压破坏。

(13)

式中，Fh为水平拉杆的极限承载力；Ascor为节点核心区箍筋的约束面积。由试件设计情况，通过线性内插可得，混凝土在三向受压状态下抗压强度的提高系数为1.09[28]，该提高系数与节点水平抗剪承载力实测值和理论值的平均比值1.115接近。基于此，作出以下假设：

(1) 计算节点核心区箍筋提供的拉力时，对箍筋的有效截面面积采取以下假设：节点核心区中心位置的箍筋全部有效，节点核心区其他位置的箍筋50%有效；

(2) 当节点核心区最终发生斜压破坏时，主压应力σ1为0。由于主压应力σ2远小于混凝土的抗压强度，因此，假定主压应力σ2为0，即不考虑中间主应力的影响。

根据库伦破坏准则，节点核心区混凝土达到剪切破坏极限状态时，破坏面上剪切应力与法向应力之间满足下列关系

τ=c+σtgφ

(14)

式中：c为混凝土的黏结力即纯剪强度；σ为作用于受剪面上的正应力；φ为内摩擦角。平面内任一点处正应力、切应力满足莫尔圆的关系。用莫尔应力圆表示，上述条件相当于破坏应力圆将与一条称为强度包络线的直线相切，如图4所示。发生滑动破坏时，可得：

图4 滑动破坏时的应力状态

(15)

(16)

(17)

图5 混凝土抗剪强度计算模型

该计算模型表明，轴压比n=0.5是临界点。动态荷载作用下，荷载作用时间极短，微裂缝的发展体现出一定的“迟滞作用”，材料只能通过提高应力的方式来达到消耗能量的目的，损伤出现迟滞现象，损伤的滞后延缓了混凝土的软化效应，并且使得混凝土内部裂纹发展不充分，因而导致骨料破坏，混凝土强度提高[29]。根据CEB[30]的规定，考虑应变率效应，单轴受压时混凝土动态强度增长因子DIFfc可由下列公式求得

(18)

(19)

3 试验现象

快速加载条件下，节点组合体内产生三类裂缝：第一类为框架梁、框架柱内的弯曲垂直裂缝及剪切斜裂缝；第二类是节点核心区由对角线斜向主拉应力引起的交叉斜裂缝；第三类是由于梁筋黏结滑移，在靠近梁端节点角部产生的斜裂缝，或者节点核心区侧边，梁端内的垂直裂缝。加载过程中，框架梁内首先产生弯曲垂直裂缝及剪切斜裂缝，其次，节点核心区内产生交叉斜裂缝，随着加载位移的不断增大，节点组合体两侧产生塑性铰，最终，节点核心区箍筋屈服，随后，混凝土被压碎剥落。这与软化拉-压杆模型理论预测结果一致。

如图6所示，不同轴压比水平下，梁柱节点组合体的破坏形态相同，但随着轴压比的逐渐增大，节点核心区裂缝的开展受到遏制，裂缝数量不断减少，节点核心区的剪切变形减小，同时，节点核心区斜裂缝与水平方向的夹角不断增大(黑色箭头所示)。原因在于，本次试验研究轴压比范围内，轴压比的增大，对节点组合体的抗剪性能起有利作用，增大轴压比可以改善节点核心区梁筋贯穿段的黏结性能，减小钢筋与混凝土之间的黏结滑移，从而限制节点核心区裂缝的开展。此外，低轴压比水平下，节点核心区破坏严重，较高轴压比水平下，梁端塑性铰区域破坏更加严重，而节点核心区破坏程度降低。

(a) JM2-7

(b) JM2-17

(c) JM2-4

(d) JM2-8

4 试验结果

4.1 荷载-位移滞回曲线

左右梁端反对称加载，取其中一端试验结果，绘制滞回曲线如图7所示。由图7可知，轴压比虽不同，但荷载-位移滞回曲线均表现出不同程度的“捏缩”效应。产生这种现象的原因在于，节点组合体内部梁筋的黏结滑移，以及反向加载时刚度的退化。

(a) JM2-7(n=0.05,v=40 mm/s)

(b) JM2-7(n=0.10,v=40 mm/s)

(c) JM2-4(n=0.15,v=40 mm/s)

(d) JM2-8(n=0.25,v=40 mm/s)

图7 梁柱节点荷载-位移滞回曲线

Fig.7 Load-deflection hysteretic curves of beam-column joints

4.2 水平剪力

梁柱节点水平剪力大小可按《建筑抗震设计规范》GB 50011—2010[31]附录D的规定计算：

(20)

图8 不同轴压比下梁柱节点水平剪力大小

Fig.8 Horizontal shear force of beam-column joints under different axial compression ratios

4.3 刚度退化

刚度退化可用环线刚度来衡量。试件JM2-7正反向加载时的环线刚度，计算结果如图9所示。由图可知，相同位移水平下，正向加载的环线刚度始终大于反向加载的环线刚度，原因在于，加载过程中基体材料裂缝的滋生和发展、钢筋的部分弹塑性发展、钢筋与基体材料之间的黏结滑移以及节点组合体开裂后因塑形变形产生的残余内应力等引起节点内部不断损伤。

图9 不同加载方向刚度退化对比

4.4 强度退化

强度退化可以用承载力降低系数λj来衡量[32]，定义承载力降低系数如下

(21)

式中:Pj,min为位移为Δj时，第2循环峰值荷载；Pj,max为位移为Δj时，第1循环峰值荷载。以试件JM2-7、JM2-4、JM2-8为例，研究Δ/Δy≤5时的强度退化，其结果如图10所示。由前面的荷载-位移滞回曲线可知，节点组合体峰值荷载处的位移为4倍屈服位移左右。从图10可以看出，随着位移的增大，承载力降低系数由于混凝土内部损伤逐渐加重而逐渐减小。Δ/Δy≤4时，轴压比较大的试件，其承载力降低系数较大，说明轴压比增大有利于节点组合体抗剪，Δ/Δy>4时，轴压比较大的试件，其承载力降低系数下降速度较快，其值反而小于轴压比小的试件，说明节点组合体骨架曲线下降段更陡。

图10 不同轴压比下强度退化曲线

4.5 能量耗散

等效黏滞阻尼系数只反映试件滞回环的饱满程度，与承载力无关。对于承载力不同的试件，从某种角度上来讲，采用等效黏滞阻尼系数更能准确评价试件的耗能能力。参照文献[25]的计算公式，不同轴压比下节点组合体的等效黏滞阻尼计算结果，如图11所示。

图11 不同轴压比下等效黏滞阻尼曲线

Fig.11 Curves of equivalent viscous damping under different axial compression ratios

由图11可知，Δ/Δy≤3时，等效黏滞阻尼系数均随位移的增大而增大，说明节点组合体耗散的能量增多，损伤加重。Δ/Δy>3时，等效黏滞阻尼系数随位移的增大而减小，且轴压比增大时，等效黏滞阻尼系数降低的幅度变大，但在Δ/Δy≤7范围内，较高轴压比下节点组合体的等效黏滞阻尼系数始终大于低轴压比下节点组合体的等效黏滞阻尼系数。说明峰值荷载之后，试件的损伤加重，节点组合体耗能能力减弱，但轴压比增大时，试件耗能能力相对增强。

5 结 论

(1) 软化拉-压杆模型可用于预测节点组合体的抗剪承载力及破坏形态。基于软化拉-压杆模型、库伦破坏准则、莫尔圆理论、节点组合体受力模型，推导的剪压复合受力状态下混凝土抗剪强度计算模型，可用于预测考虑材料应变率效应后，轴压比对节点组合体抗剪承载力的影响规律。

(2) 不同轴压比水平下，节点组合体均产生三类裂缝，其破坏形态相同。但随着轴压比的逐渐增大，节点核心区裂缝的数量不断减少，节点核心区的剪切变形减小，节点核心区斜裂缝与水平方向的夹角不断增大。此外，低轴压比水平下，节点核心区破坏严重，较高轴压比水平下，梁端塑性铰区域破坏更加严重，而节点核心区破坏程度降低。

(3) 相同位移水平下，正向加载的环线刚度始终大于反向加载的环线刚度。轴压比的增大，对节点组合体抗剪承载力起有利作用，但较高应变率对节点组合体的有利作用，致使轴压比的有利作用空间变小。峰值荷载之后，试件的损伤加重，节点组合体耗能能力减弱，但轴压比增大时，试件的耗能能力相对增强。