基于全光纤激光干涉测速技术的拉氏反分析方法应用于脆性材料动态本构关系研究

丁圆圆, 张 振, 赖华伟, 王永刚

(宁波大学 冲击与安全工程教育部重点实验室， 浙江 宁波 315211)

研究冲击载荷下材料的动态本构关系最常用的有两类实验方法:① 分离式Hopkinson压杆(Split Hopkinson Pressure Bar, SHPB)实验;② 波传播反演分析实验。SHPB实验技术[1-2]是建立在两个基本假定基础上，即试件沿长度方向应力/应变均匀性分布假定和一维应力波假定。然而，对混凝土、岩石、陶瓷等脆性材料而言，这两个假定均受到了挑战[3-4]。由于脆性材料破坏应变小，试件直径大，同时又对应力集中非常敏感，这些因素将导致上述两个基本假定难以满足。波传播反演分析实验技术是基于材料中多点测量的波传播信息来反推材料的本构关系，应用较广泛的是拉格朗日反分析方法(以下简称拉氏反分析方法)[5-6]。拉氏反分析方法的基本思想是：在试件的不同Lagrange 位置上设置传感器，记录试件中传播的某力学量(应力、应变或质点速度等)的波剖面，再利用守恒方程计算得到其他未知的力学量，进而得到材料的动态应力-应变曲线。拉氏反分析方法不需要事先作任何的本构关系假定和其他任何假定，在研究混凝土、陶瓷、岩石等脆性材料的动态本构方面具有优势。陶为俊等[7]利用沿时间逐步求解应力的拉氏反分析方法得到了混凝土材料率相关的应力-应变曲线。张磊等[8]采用基于多点应变测量数据的拉氏反分析方法也研究了混凝土材料动态本构关系，讨论了应变率效应。蒋国平等[9-10]采用一级轻气炮对钢纤维混凝土进行了冲击压缩实验，通过锰铜应力计监测不同位置的应力波形，再利用拉氏反分析方法得到了一维应变条件下钢纤维混凝土材料的应力-应变曲线和高压状态方程。林英睿等[11]对爆炸球面波加载下有机玻璃和花岗岩试件中实测应力剖面数据进行拉氏反分析，研究了有机玻璃和花岗岩材料的动态本构关系。

近年来，在理论和数据处理方面，拉氏反分析方法还在不断的改进和完善[12-13]，但在力学量多点测量技术方面进展较缓慢，仍然局限于是应力时程和应变时程测量，这大大制约了该方法在实验力学领域中更广泛的应用。采用锰铜应力计或者PVDF应力计进行多点应力时程测量时，应力计需要嵌入到试件内部，导致试件中出现了人为界面，该界面会对应力波传播带来比较严重的影响，从而降低了拉氏反分析的精度。应变片电测法获得应变时程测量时，但由多点应变波剖面积分求解速度信息和应力信息时必须有应变边界条件和应力边界条件，这给数据处理带来了双重困难，同时也会引入较大误差。近年来，人们又发展了磁电式质点速度计来监测试件中质点速度时程[14]。相比应力测量和应变测量，质点速度测试的精度和可靠性较高。事实上，除了磁电式质点速度计，还有一种广泛使用的质点速度测试技术——激光干涉测速技术[15]。早期的激光干涉测试系统光路复杂，只能进行单点测量。为了实现多点测量，人们发展了多探头全光纤激光干涉测速仪[16]。然而，迄今为止，该技术在拉氏反分析方法中并没有得到应用。

本文以 SHPB装置作为加载手段，采用多探头全光纤激光干涉测速仪，以激光斜入射方式来同时监测试件上不同欧拉位置上的质点速度时程。基于一维应力波理论，建立欧拉质点速度与拉格朗日质点速度之间换算关系。最后，基于试件上不同质点的拉格朗日质点速度时程，建立脆性材料动态本构的拉氏反分析实验技术，并PMMA材料为例，考察该新技术的可靠性和实用性。

1 多探头激光干涉测速系统的原理

图1给出了多探头激光干涉测试系统的测试原理示意图，从He-Ne激光器中发出频率为f0的激光(波长1 550 nm)进入1×N光纤分束器Coupler 1后被分成N路，构成N个测量通道，其中单个通道的光路如图1虚线框内部分所示。一个通道输入光经过一个1×2光纤分束器Coupler 2后，一部分激光作为参考光经由声光调制器直接进入Coupler 3，频率不变，而一部分激光通过光纤环行器2端注入探头，并从探头照射到待测移动目标上，探测光在目标上发生反射，部分反射光被探头收集，反射信号光发生多普勒频移，频率变为fs，再次进入环形器后，作为信号光从端口3进入Coupler 3，信号光和参考光合束后产生干涉，干涉光进入探测器，经光电转换后由高带宽的示波器记录。多普勒频移fd和目标运动速度之间关系为

u(t) =λ(fs-f0) /2 =λfd/2

(1)

式中:λ激光的波长。采用短时傅里叶变换方法对示波器记录的激光干涉信息进行频域分析，提取出多普勒频移，即可利用式(1)得到被测目标的运动速度。速度时程是隐藏在激光干涉信号的频域中，与光强变化无关。

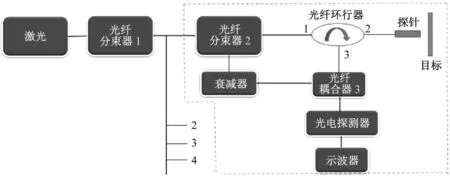
图1 多探头激光干涉测速系统的原理示意图

2 拉氏反分析方法原理

在拉格朗日坐标下，一维应力波的守恒方程为

质量守恒方程

(2)

动量守恒方程

(3)

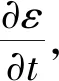
(4)

改写

(5)

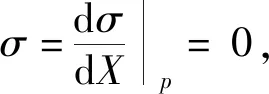
3 实验方案

图2给出了拉氏反分析实验装置的示意图。加载系统是基于分离式Hopkinson压杆搭建的，即通过高压气枪发射200 mm长的铝合金子弹，子弹撞击铝合金入射杆后，在入射杆中产生了有一定脉宽的应力脉冲，应力脉冲从入射杆传入PMMA长杆试件。在实验中，为了调整应力脉冲的波形，在入射杆前端增加了环形无氧铜垫片(外径8 mm，内径4 mm,厚度1 mm)作为波形整形器。为了监测长杆试件不同位置处轴向质点速度时程，我们采用了激光斜入射测试技术，如图2所示。在长杆试件靠近杆端附近布置了三个斜入射的激光光纤探头，探头与杆的轴向之间夹角为α，每个探头之间的间距为100 mm。由于速度时程是隐藏在激光干涉信号的频域中，与光强变化无关，激光照射在运动物体表面上时不需要发生镜面反射，因此激光可以斜入射长杆试件表面测量点。通过在测量点粘贴漫反射薄膜，提高反射激光被探头吸收的效率，使得部分带频移信息的激光被光纤接受到，再通过频谱分析即可测得沿激光照射方向的质点速度vmeas(t)，再基于矢量分解原理，换算为杆中沿轴向的质点速度vaxial(t)，即：

(6)

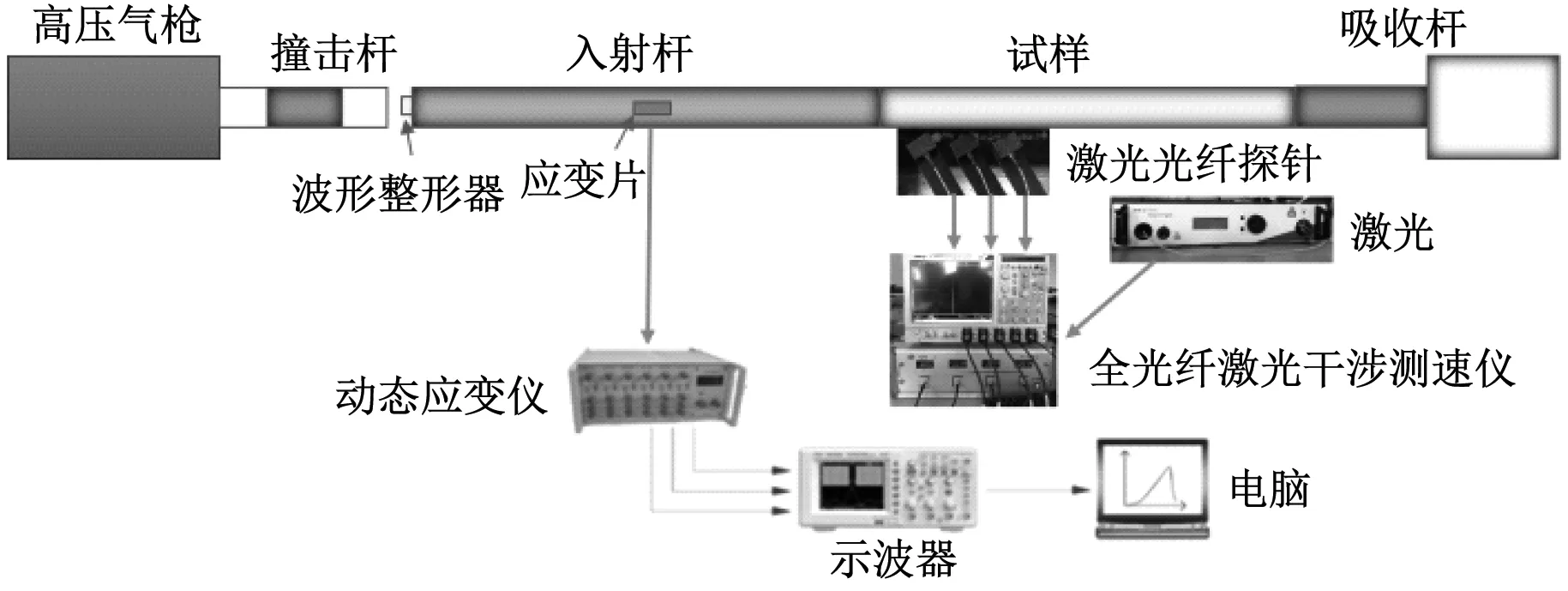
图2 基于SHPB加载系统的拉氏反分析实验平台

多探头全光纤激光干涉测速仪由中国工程物理研究院流体物理研究所研制，红外激光作为光源，激光波长1 550 nm，测速范围0.1～4 000 m/s。

4 实验结果与讨论

4.1 数据处理

图3给出了典型的高带宽示波器记录的激光干涉原始电压信号，对电压信号进行短期傅里叶变换，得到信号频率图谱，再进行滤波处理后转化为速度时程，如图4所示。

图3 激光干涉原始电压信号

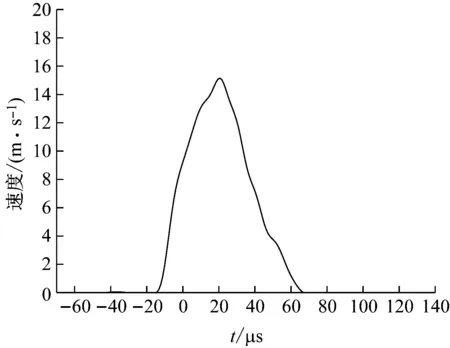
图4 试件上质点速度时程曲线

4.2 欧拉质点速度与拉格朗日质点速度换算关系

由于激光探头(见图2)的空间位置是固定的，实验中测得的质点速度是基于欧拉坐标系的，而拉氏反分析是基于拉格朗日坐标系，因此，这里首先需要讨论欧拉质点速度vE和拉格朗日质点速度vL之间的换算关系。根据一维应力波传播理论，物理量φ在拉格朗日坐标系(X,t)和欧拉坐标系(x,t)之间转换公式是

(7)

当φ为质点位移时，则

(8)

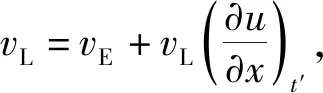
整理后，得到

vL=(1+ε)vE

(9)

4.3 激光斜入射测试技术可靠性验证

把图2中一个激光探头前移至入射杆中部的应变片粘贴位置，斜入射角度α设定为60°。激光斜入射法测得到的质点速度vmeas(t)见图5所示。同时图5中也给出了应变片测得的应变时程。从应变时程曲线可知入射杆的应变最大值仅仅0.001，远远小于1，根据式(9)可知，vL和vE之间的差异可以忽略。根据一维弹性波理论，入射杆上应变与质点速度之间关系为

(10)

这里C0是铝合金入射杆中的弹性波波速(5×103m/s)。把质点速度vmeas(t)代入式(10)，转换为应变信息后，其与应变片测得的应变信息对比见图5所示，图中显示两者的一致性非常好，这验证了激光斜入射方法来测量轴向质点速度的可行性和可靠性。

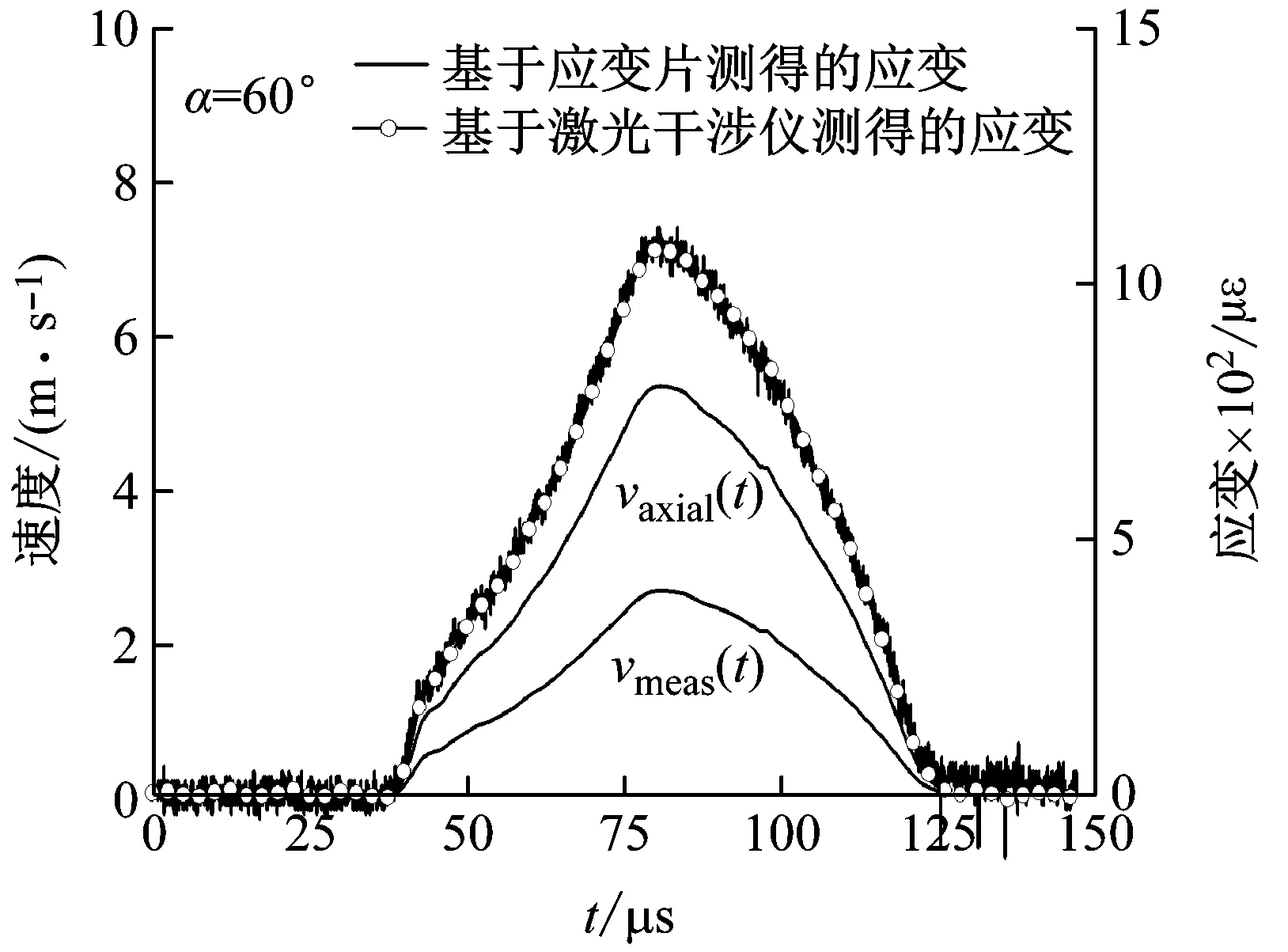
图5 激光斜入射技术可靠性验证

4.4 拉氏反分析

当拉氏反分析应用于脆性材料的动态力学性能研究，由于脆性材料的变形能力弱，破坏应变远小于1，因此一般情况下也可忽略vL和vE之间的差异。PMMA是一种典型的黏弹性材料，同时在冲击载荷下也是偏脆性的。图6是在PMMA长杆试件上测得的一组典型质点速度时程曲线。以长杆试件撞击端面为位移零点位置，相邻测量点之间距离h为100 mm，再从图6中测出相邻测量点之间起始时间差Δt约为45 μs，由此可以估算出PMMA材料中应力波传播的低应力准弹性波速C0(C0=h/Δt)约2.2×103m/s，利用式(10)可以估算出试件应变ε约1.35%，其远远小于1，因此在后续拉氏反分析中可以忽略vL和vE之间的差异。如果试件估算应变较大时，也可以利用式(10)对欧拉质点速度进行修正。另外，图6中还显示了应力波在PMMA材料中传播时质点速度峰值表现了明显地衰减，同时脉宽也在增加，这恰是应力波在黏弹性材料中传播时所表现出的典型黏性耗散和弥散特性。

按照路径线法原理，以质点速度的峰值为特征点把质点速度时程曲线分为加载区(Zone I)和卸载区(Zone II)，在每个区域中，对每条质点速度曲线进行等间距划分节点数，那么每条质点速度曲线都有N个节点，如图6所示。

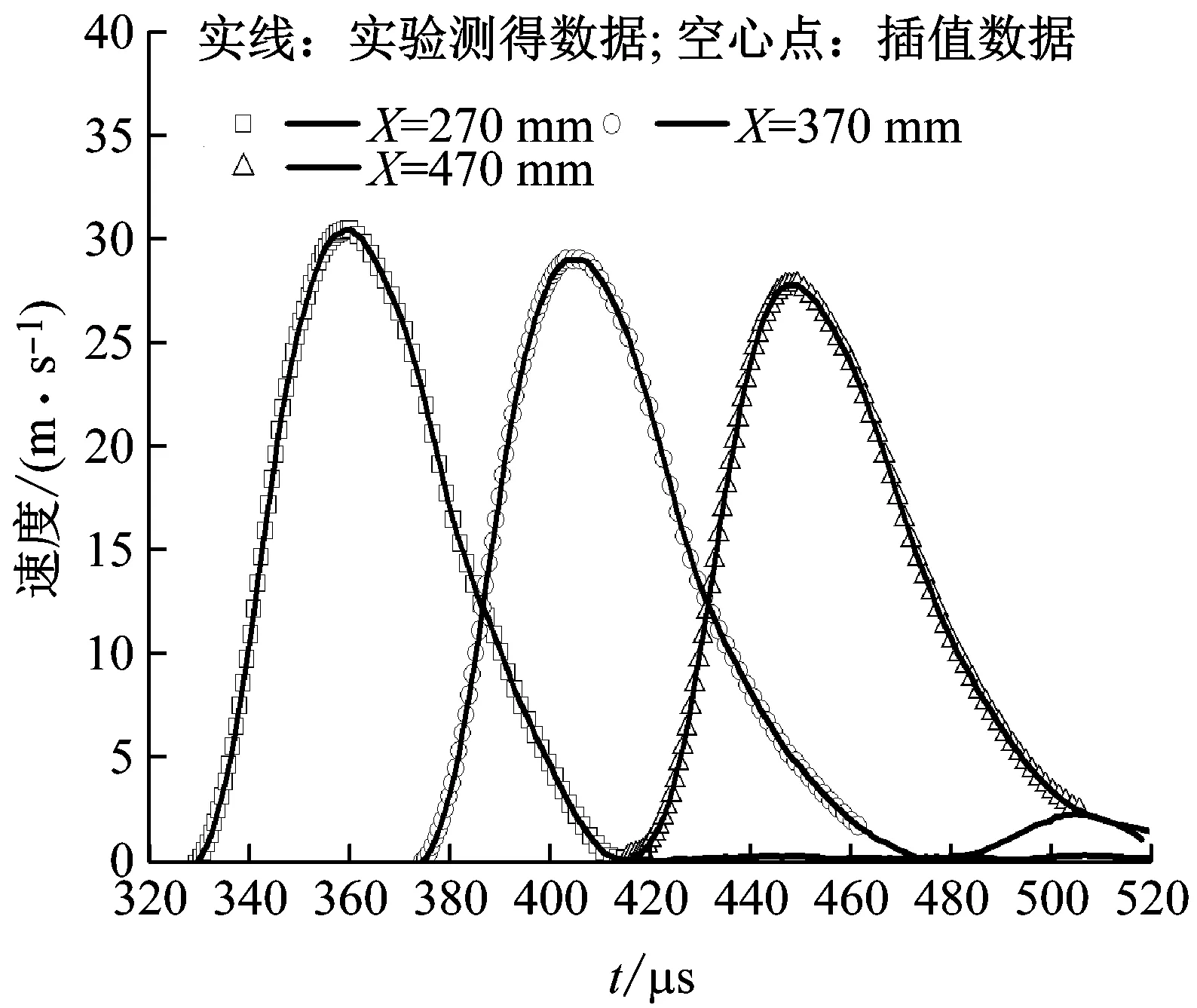
图6 质点速度时程曲线

将每条质点速度曲线所对应的节点通过光滑的曲线连接在一起，从而构造了路径线，通过这些路径线把整个速度场联系在一起，再利用式(5)来计算应力时程。基于多质点速度时程曲线，通过拉氏反分析数值求解，最终得到三个测量点的应变时程曲线和应力时程曲线，如图7和8所示。从应变时程和应力时程中消去时间，即得三个测量点处的材料应力-应变曲线，如图9所示。结果显示：PMMA的应力-应变曲线的加载段在实测小应变条件下(子弹冲击速度较低)是准线性的，但在卸载段表现出了应变滞后效应，这也归因于PMMA是一种粘弹性材料。实验中，采用波形整形器技术产生三角形加载波形，这有助于在实验过程中保持加载应变率基本恒定，通过对应变时程的加载段线性拟合得到加载应变率约为5.5×102s-1。另外，图9还给出了Hopkinson压杆实验(1.0×103s-1)和准静态压缩实验(1.0×10-3s-1)得到的应力-应变曲线，结果显示：应变率为5.5×102s-1的本实验的拉氏反分析的结果介于两者之间，反映了PMMA的力学性能具有明显的应变率效应，特别是卸载段的应变滞后现象不仅依赖应变率还依赖于应变。

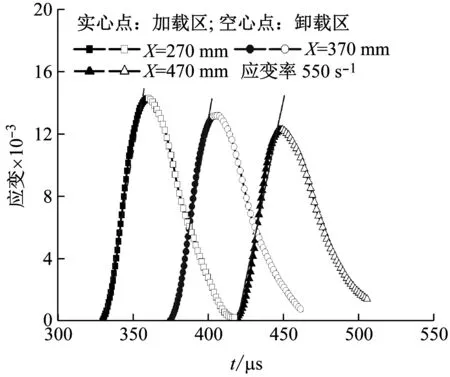
图7 应变时程曲线

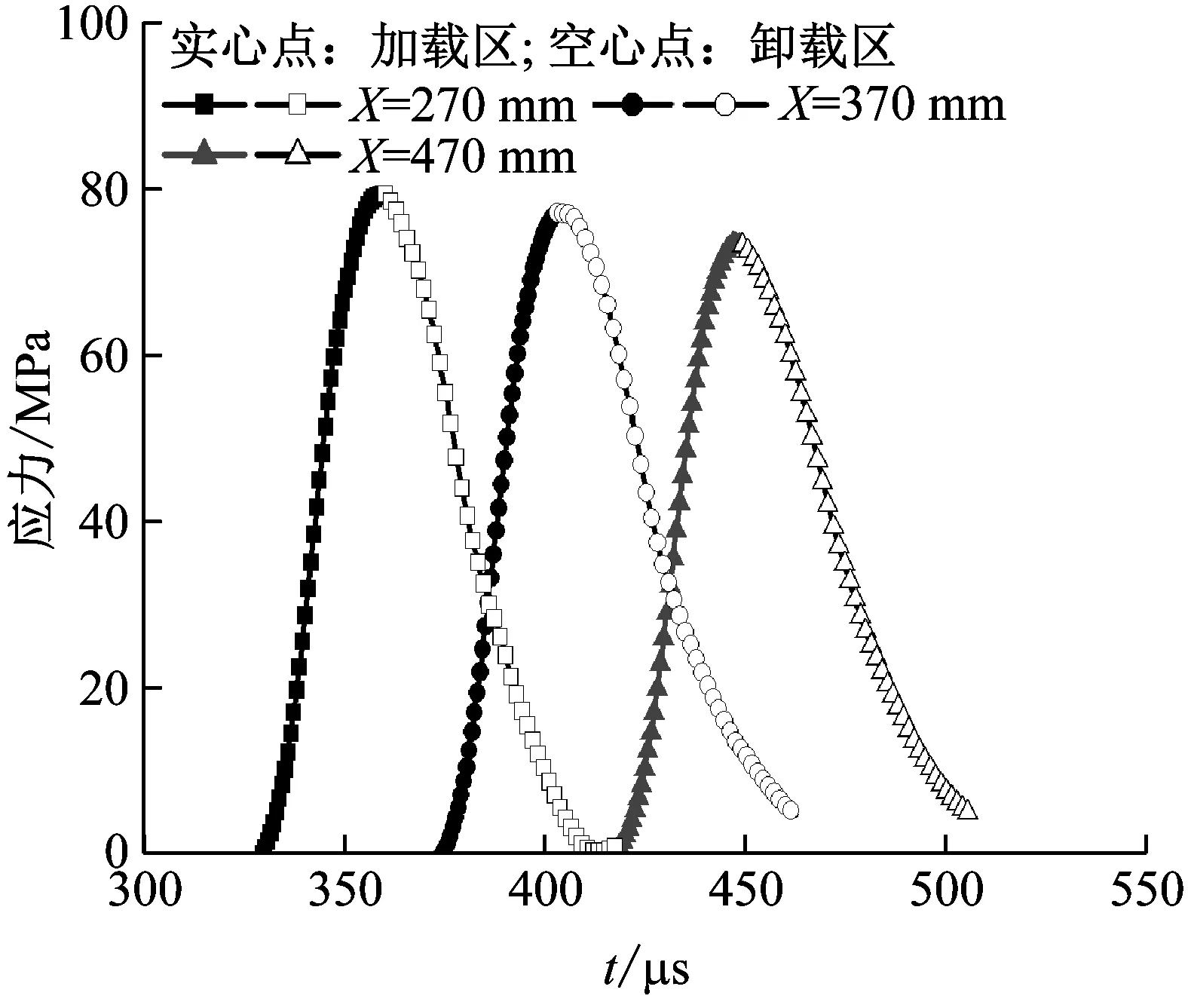
图8 应力时程曲线

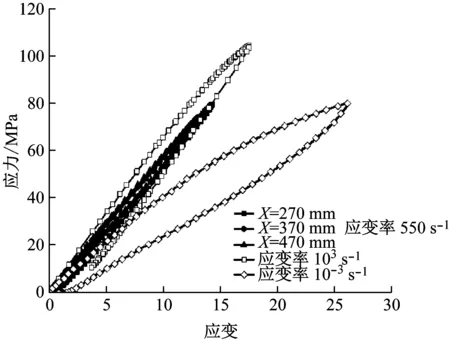
图9 不同应变率下的PMMA应力-应变曲线

5 结 论

以分离式Hopkinson压杆系统作为加载手段，借助多探头全光纤激光干涉测速技术，采用激光斜入射方法，实时监测了长杆试件上不同位置处轴向欧拉质点速度时程。基于一维应力波传播理论，建立了欧拉质点速度与拉格朗日质点速度之间的换算关系。基于激光干涉法实测的多条质点速度时程曲线，通过构建路径线，再结合零初始条件，实现了拉氏反分析的数值求解。以典型脆性黏弹性材料PMMA为例，获得了材料的动态应力-应变曲线，验证了新方法的可行性。新的拉氏反分析测试方法在脆性材料的动态力学性能研究领域中有重要的应用价值。