透视函数应用题型 发展数学建模素养*
2019-06-21安徽省枞阳县宏实中学246700朱贤良朱行斌
安徽省枞阳县宏实中学(246700) 朱贤良 朱行斌
在我国的数学教育史上,有着重视数学应用的传统,这也是我国古代数学教育的一大特色.2018年初,教育部颁发的《普通高中数学课程标准(2017年版)》将“数学建模”列为数学学科六大核心素养之一,强调对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题.实际上,我国的数学教育不仅在教育教学活动中强调数学的应用意识,在高考与各类模拟考试中,数学应用问题也一直是极为重要的题型之一.本文在教学实践的基础上,对函数应用题型进行梳理,力图为培育数学建模素养服务.
1.利用函数图象刻画实际问题
图象法是函数的表示方法之一,通过图象可以直观地反映函数的变化规律及相关性质.以生活中的实际情景为载体,精心设计函数图象问题,能有效地考查数形结合的思想与数学建模的意识.
例1-1(2013年高考湖北卷文科第5题)小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间后,为了赶时间加快速度行驶.与以上事件吻合得最好的图象是( )
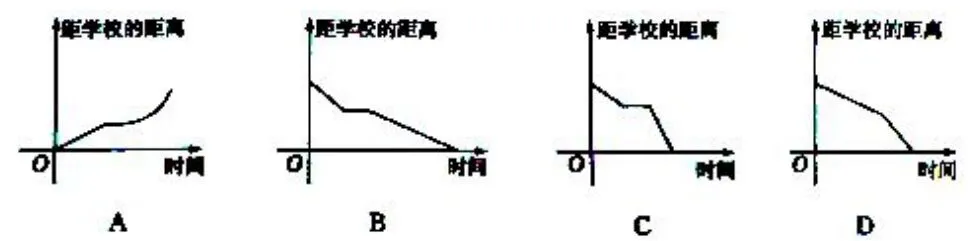
解析小明距学校的距离应逐渐减小:由于一开始是匀速行驶,故前段沿直线递减;途中停留时距离保持不变,图象为水平线段;后段加快速度行驶,则直线段比一开始下降得更快.符合前述特征的只有选项C.
点评本题以学生从小就熟悉的距离、速度、时间之间的关系为背景设置问题,考查学生从函数的角度来理解三者之间的变化关联.
例1-2(2015年高考北京卷理科第8题)汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,右图1描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.下列叙述中正确的是( )
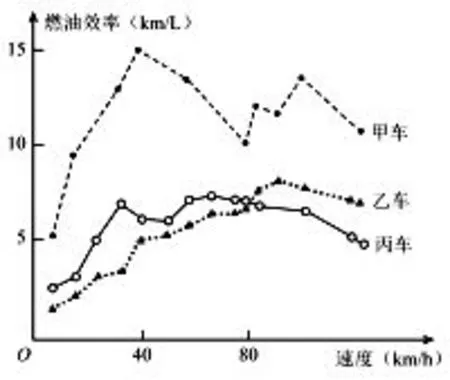
图1
A.消耗1升汽油,乙车最多可行驶5千米
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D.某城市机动车最高限速80千米/小时.相同条件下,在该市用丙车比用乙车更省油
解析甲、乙、丙三辆汽车的“燃油效率”随速度的变化而不同,图象直观反应了三辆汽车在不同速度下每消耗1升汽油所行驶的里程状况.从图象来看,当速度超过40时,乙车的“燃油效率”大于5,即在速度超过40千米/小时的条件下,乙车每消耗1升汽油,所行驶的里程将大于5千米,故A项错误;当速度相同时,甲车的“燃油效率”最高,即以相同速度行驶时,每消耗1升汽油,甲车所行驶的里程最远,故甲车行驶相同路程所消耗汽油最少,B项错误;甲车的速度为80时,其“燃油效率”为10,即以80千米/小时的速度行驶时,每消耗1升汽油,甲车行驶的里程为10千米,故此速度下行驶1小时,行驶的里程为80千米,需消耗8升汽油,C项错误;当速度不超过80时,丙车比乙车的“燃油效率”更大,即相同速度的前提下,每消耗1升汽油,丙车比乙车所行驶的里程更远,故用丙车比用乙车更省油,D项正确.
点评在环境保护、能源危机的日益突出的实际背景下,本道试题以“燃油效率”为命题的切入点,引导学生分析影响“燃油效率”的速度因素,既具有现实意义,又能有效检测学生对函数关系的准确把握能力.
例1-3(2006年高考江西卷理科第12题)某地一年内的气温Q(t)(单位:°C)与时间t(月份)之间的关系如图2所示,已知该年的平均气温为10°C.令C(t)表示时间段[0,t]的平均气温,C(t)与t之间的函数关系用下列图象表示,则正确的应该是( )
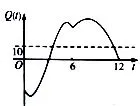
图2
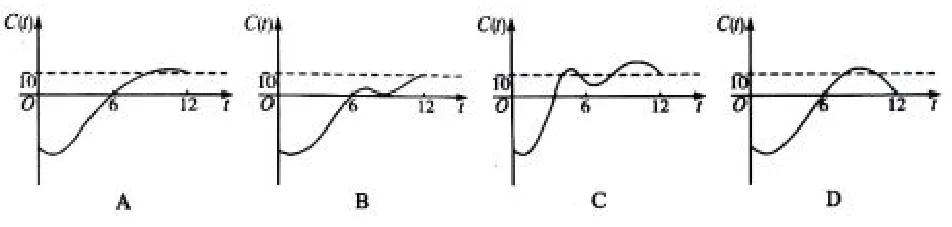
解析全年的平均气温为10°C,即C(12)=10,故D项错误;6月份之前的平均气温肯定低于10°C,则C(6)<10,故C项错误;12月份之前的一段时间内气温低于10°C,故在此段时间之前的那一段时间内C(t)>10,故B项错误.所以,正确选项为A项.
点评函数关系是一类常见的变量间的关系,但理清变量之间的函数关系、把握其变化规律却并不容易.本题要求考生通过函数图象来刻画变量间的关系,必须先读懂图象,认清Q(t)与t之间的关系,进而准确把握C(t)的变化规律,运用图象来直观表示C(t)与t之间的函数关系.
2.构建函数模型解决实际问题
随着时代的发展与知识的更新,函数应用问题中的背景与模型越来越新颖.在求解函数应用题时,很重要的一步是准确到位地理解问题的实际背景,通过构建数学模型,实现实际问题的数学化.需要留心的是,建模之后的函数问题应在定义域内完整地进行解答,忽视定义域的限制会导致错误.
例2-1(2016年高考四川卷理科第5题文科第7题)某公司为了激励创新,计划逐年加大研发资金投入.若该公司2015年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是(参考数据:lg1.12≈0.05,lg1.3≈0.11,lg2≈0.30)( )
A.2018年 B.2019年 C.2020年 D.2021年
解析设2015年后的第n年该公司投入的研发资金为y万元,则y=130·(1+12%)n.依题意,130·(1+12%)n>200,即,两边取对数得n·lg1.12>lg2-lg1.3,故.所以,从2019年开始,该公司投入的研发资金开始超过200万元.
点评以指数函数模型为背景的增长率问题与社会、经济的发展息息相关,从小学开始就伴随我们数学学习的全过程.本题在建立指数函数模型后,要灵活运用对数的运算来解决数学问题,并根据数学问题的运算结果合理解释实际问题.
例2-2某公司租地建仓库,每月土地费用与仓库到车站距离成反比,而每月货物的运输费用与仓库到车站距离成正比.如果在距离车站10km处建仓库,则土地费用和运输费用分别为2万元和8万元,那么要使两项费用之和最小,仓库应建在离车站( )
A.5km处 B.4km处 C.3km处 D.2km处
解析设仓库与车站的距离为xkm,每月的土地费用与货物的运输费用分别为万元、k2x万元.根据题意,当x=10时,解得则每月土地费用和运输费用之和为(当且仅当即x=5时,等号成立).所以,当仓库建在离车站5km处时,两项费用之和取得最小值8万元.
点评本题是函数应用中费用最少的问题,涉及正比例函数、反比例函数与对勾函数等模型.正确解决本题,既需要具备建立数学模型的能力,还必须能借助基本不等式等知识求得最值.
例2-3(2018年高考上海卷第19题)某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时.某地上班族S中的成员仅以自驾或公交方式通勤.分析显示:当S中x%(0<x<100)的成员自驾时,自驾群体的人均通勤时间为
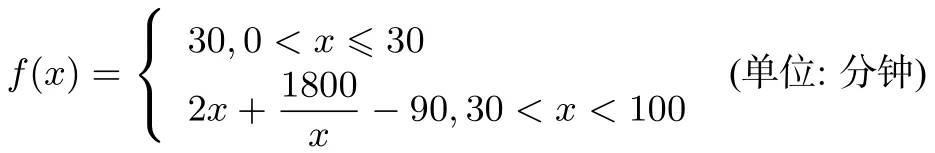
而公交群体的人均通勤时间不受x影响,恒为40分钟(0<x<100).试根据上述分析结果回答下列问题:
(1)当x在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
(2)求该地上班族S的人均通勤时间g(x)的表达式,讨论g(x)的单调性,并说明其实际意义.
解析(1)公交群体的人均通勤时间少于自驾群体的人均通勤时间,即f(x)>40.当0<x≤30时,f(x)=30<40,显然不符合要求;当30<x<100时,由得x2-65x+900>0,解得x>45或x<20,故45<x<100.所以,当45<x<100时,公交群体的人均通勤时间少于自驾群体的人均通勤时间.
(2)当0<x≤30时,40-0.1x;当30<x<100时,·x%+40·(1-x%)=0.02x2-1.3x+58.所以,
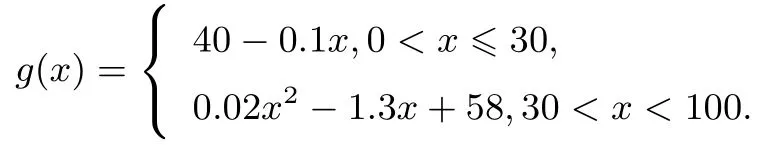
结合g(x)的图象可知,g(x)在区间(0,32.5]上递减,区间[32.5,100)上递增.其实际意义是:当自驾群体比例少于32.5%时,越多的人自驾,平均通勤时间越短;当自驾群体比例多于32.5%时,越多的人自驾,平均通勤时间越长.
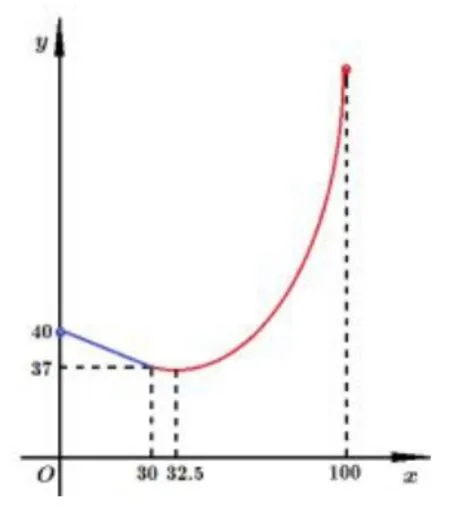
图3
点评本题以生活中的交通拥堵、通勤时间为情境设置数学应用问题,将分段函数、一次函数、分式函数、二次函数等众多函数模型融于一题,综合考查学生阅读审题、数学建模、用数学知识解释现实问题等方面的能力.
3.借助导数求解生活中的优化问题
导数在实际生活中有着广泛的应用,利用导数可以求出实际生活中的一些最值问题,如利润最大、生产效率最高、用料最少、耗油量最少等问题.我们把这类寻求最佳方案或最佳策略的实际问题,称为优化问题.
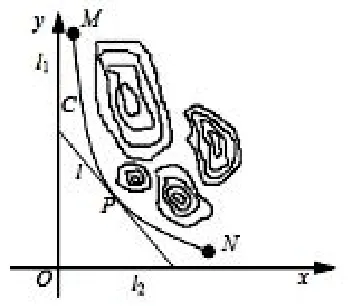
图4
例3-1(2015年高考江苏卷第17题)某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路的山区边界的直线型公路.记两条相互垂直的公路为l1,l2,山区边界曲线为C,计划修建的公路为l.如图4所示,M,N为C的两个端点,测得点M到l2,l1的距离分别为5千米和40千米,点N到l1,l2的距离分别为20千米和2.5千米.以l1,l2所在的直线分别为x,y轴,建立平面直角坐标系xOy.假设曲线C符合函数(其中a,b为常数)模型.
(1)求a,b的值;
(2)设公路l与曲线C相切于P点,P的横坐标为t.
①请写出公路l长度的函数解析式f(t),并写出其定义域;
②当t为何值时,公路l的长度最短?求出最短长度.
解析(1)由题意知,点M,N的坐标分别为(5,40),(20,2.5).将其分别代入得解得
(2)①由(1)知曲线C的函数关系式为x≤20),则.因为切点P的坐标为故切线即公路l所在直线的方程为分别(令x)=0(,y=0,由)此可得公路l与x,y轴的交点依次为.所以,公路l长度的函数解析式为,其定义域为t∈[5,20].
点评本题在建立函数模型的过程中,需要根据导数的几何意义求得切线的方程,进而求得公路的长度;建立函数模型之后,再运用导数这一工具研究函数的单调性,解决函数的最值问题.将曲线的切线、函数的单调性、最值等问题综合设置在实际的问题情境之中,综合性强,能有效地考查学生对导数工具性的掌握情况.
例3-2(2008年高考江苏卷第17题)如图5,某地有三家工厂,分别位于矩形ABCD的顶点A,B及CD的中点P处,已知AB=20km,BC=10km.为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且与A,B等距离的一点O处,建造一个污水处理厂,并铺设排污管道AO,BO,PO.记排污管道的总长为ykm.
(1)按下列要求写出函数关系式:
①设∠BAO=θ(rad),将y表示成θ的函数关系式;
②设PO=x(km),将y表示成x的函数关系式.
(2)请你选用(1)中的一个函数关系,确定污水处理厂的位置,使铺设的排污管道的总长度最短.
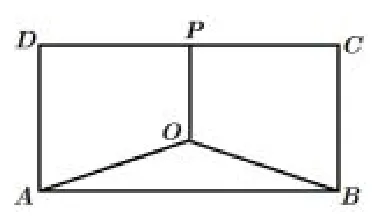
图5
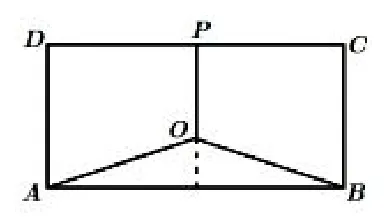
图6
解析(1)①设∠BAO=θ(rad),则OA=OB=,OP=10-10tanθ,故;
②设PO=x(km),则OA=OB=,故y=x+.
(2)选择第①个函数关系式:
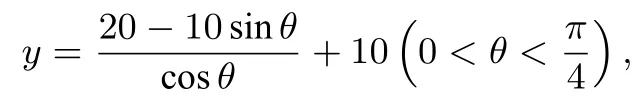
则
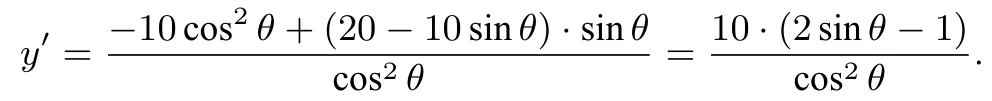
点评在建立函数模型之前,自变量的选择显得十分重要.倘若自变量选择得不合理,会导致函数模型难于建立或者最值不易求取.本题之所以选择第①个函数模型求取最值,就是基于两个函数模型中最值求取难度的权衡.
例3-3(2011年高考山东卷文理科第21题)某企业拟建造如图7所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的容积为立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元,设该容器的建造费用为y千元.
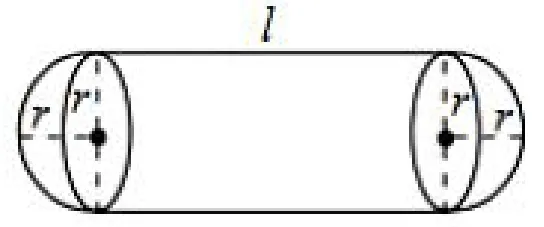
图7
(1)写出y关于r的函数表达式,并求该函数的定义域;
(2)求该容器的建造费用最小时的r.
解析(1)因为容器的容积为,则,故中间圆柱的侧面积为S1=2πrl=2π·,左右两端两个半球的表面积为S2=4πr2.所以,容器的建造费用为.又l≥2r,则,解得0<r≤2,即函数的定义域为(0,2].
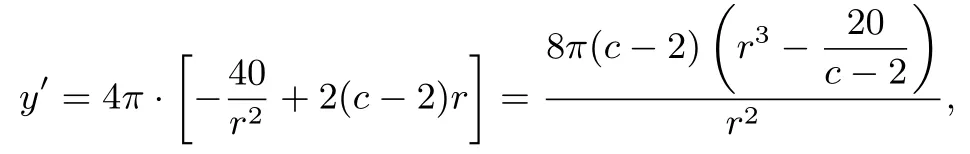
其中0<r≤2,c>3.由y′=0得,.
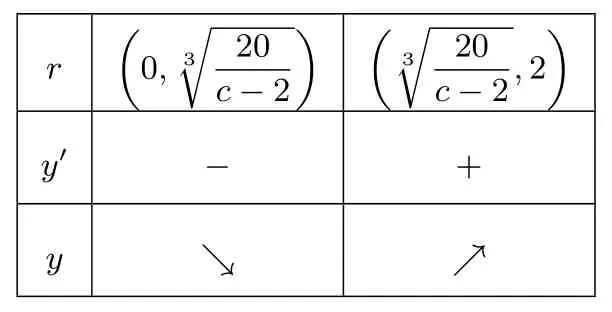
表1
点评本题在建立函数模型后,易错点有二:一是求取定义域,要考虑到l≥2r与r>0;二是求最值时要考虑定义域的限制,极值点未必落在定义域(0,2]内,要注意分类讨论思想的考查.
数学模型搭建了数学与外部世界联系的桥梁,是数学应用的重要形式.数学建模是应用数学解决实际问题的基本手段,也是推动数学发展的动力.在日常生活和学习中,要有意识地用数学语言表达现实世界,发现和提出问题,感悟数学与现实世界的关联,并学会用数学模型解决实际问题,积累数学实践的经验,增强创新意识和科学精神.
