初中数学开放探究题的类型及解题策略

（山东省枣庄市第九中学）

数学中的开放探究题，是指命题中缺少一定的条件或未给出明确的结论，需要经过补充、猜想、推断，并加以证明的问题.由于这类问题的知识覆盖面广，综合性强，解题方法灵活，再加上题型新颖，要求学生具备扎实的基础知识和较强的数学能力，从而使数学开放探究题成为考试中的一种常见题型.下面结合几道例题介绍开放探究题的常见类型及其解题策略.

一、条件开放探究题

条件开放探究题是给出问题的结论，但没有给出充分的条件，要求给出或补充使问题结论成立的条件.

解题策略是执果索因，首先要从结论出发，考虑结论成立时所要满足的条件，再结合图形及其性质逆向推导，把可能成立的条件一一列出，从而寻找出所求条件.

例1已知：如图1，在菱形ABCD中，点E，O，F分别是边AB，AC，AD的中点，连接CE，CF，OE，OF.

图1

（1）求证：△BCE≌△DCF.

（2）当AB与BC满足什么关系时，四边形AEOF是正方形？试说明理由.

分析：（1）由两个三角形的位置，借助四边形ABCD是菱形，且点E，O，F分别是边AB，AC，AD的中点，寻找对应相等的边和角即可.

（2）要使四边形AEOF是正方形，根据条件可知四边形AEOF是菱形，因此AB与BC应满足的条件是AB⊥BC.

证明：（1）略.

（2）当AB⊥BC时，四边形AEOF是正方形.理由如下.

由已知得AE=OE=OF=AF.

所以四边形AEOF是菱形.

因为AB⊥BC，OE∥BC，所以OE⊥AB.

所以∠AEO=90°.所以四边形AEOF是正方形.

【评析】解答条件开放探究题需要运用逆向思维，因此学生要掌握一些基本公式、判定定理、性质定理和重要结论成立的条件，借助数形结合思想将问题合理转化，寻找需要的条件，从而解决问题.

二、结论开放探究题

结论开放探究题是给出已知条件，根据条件探索相应的结论，符合条件的结论往往呈现多样性，或者有相应的结论需要进行推断，或者要求探索条件在变化时的结论.

解决这类问题的一般策略是由因导果，即从分析题意入手，顺向推理，或者根据题目提供的信息，通过观察、计算、联想、归纳、合情推理，得出结论.

例2 已知△ABC与△DEC是两个大小不同的等腰直角三角形.

（1）如图2（1），连接AE，DB，试判断线段AE和DB的数量和位置关系，并说明理由；

（2）如图（2），连接DB，将线段DB绕点D顺时针旋转90°到DF，连接AF，试判断线段DE和AF的数量和位置关系，并说明理由.

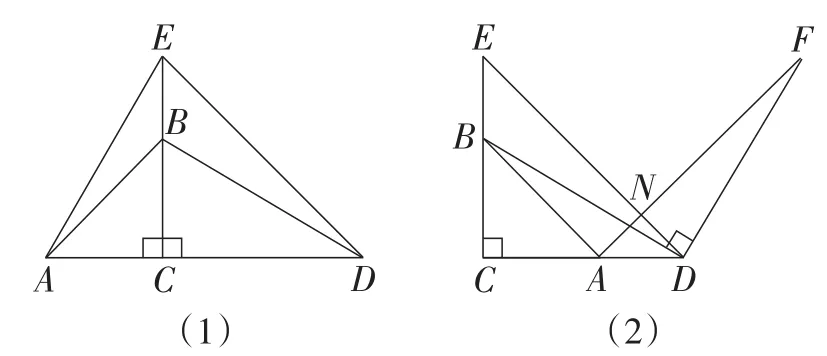
图2

分析：（1）观察图形的特点，根据AE，DB的位置选择适当的图形，列出条件，由Rt△ACE≌Rt△BCD，寻找结果；

（2）借助第（1）小题的方法和结果，探索线段DE和AF的数量和位置关系.

解：（1）AE=DB，且AE⊥DB.理由如下.

如图3，延长DB交AE于点M，

图3

因为CA=CB，CE=CD，∠ACE=∠BCD=90°，

所以 Rt△ACE≌Rt△BCD.

所以AE=DB，∠AEC=∠BDC.

又因为∠AEC+∠EAC=90°，

所以∠BDC+∠EAC=90°.

在△AMD中，得∠AMD=90°.

所以AE⊥DB.

（2）DE=AF，且DE⊥AF.理由如下.

如图2（2），设ED与AF相交于点N，

由题意可得BE=AD.

因为∠EBD=90°+∠BDC，∠ADF=90° +∠BDC，

所以∠EBD=∠ADF.

又因为DB=DF，

所以△EBD≌△ADF.

所以DE=AF， ∠E=∠EDC=∠FAD=45°.

所以∠AND=90°，即DE⊥AF.

【评析】解此类问题采用的方法是根据条件做出猜想并加以证明.一般情况下，这类问题对学生的逻辑思维能力要求较高，突出对探索、归纳、推理能力的考查.对于判断一个结论是否成立的问题，有时需要分情形加以分类讨论.若学生对学习过的公式、定理等基础知识能熟练运用，则有助于解决此类问题.

三、规律开放探究题

规律开放探究题的基本特征是给出若干数、式、函数或图形，以及它们的变化特点等，探究有关对象所具有的规律性或不变性的结论.

对于此类题，解决问题的策略是根据已知条件提供的信息，通过观察、归纳、类比、分析，即运用从特殊到一般的推理方法探究更一般的结论，然后再给出证明.

图4

（1）将矩形OCDE沿AB折叠，点O恰好落在边CD上的点F处.

①求点F的坐标；

②试直接写出抛物线的函数表达式；

（2）将矩形OCDE沿着经过点E的直线折叠，点O恰好落在边CD上的点G处，连接OG，折痕与OG交于点H，点M是线段EH上的一个动点（不与点H重合），连接MG，MO，过点G作GP⊥OM于点P，交EH于点N，连接ON.点M从点E开始沿线段EH向点H运动，至与点N重合时停止，△MOG和△NOG的面积分别表示为S1和S2，在点M的运动过程中，S1·S2（即S1与S2的积）的值是否发生变化？若变化，直接写出变化的范围；若不变，直接写出这个值.

分析：（1）因为点F的位置是由A，B两点确定的，A，B两点的坐标都隐含在抛物线的解析式中，由此先求出m的值，再求点F的坐标即可；

（2）如图5，观察图形的特点，当动点M从点E开始沿线段EH向点H运动，可以发现∠NGH与∠OMH都是∠MOG的余角，所以∠NGH与∠OMH保持相等.故点G是解题的关键点.以点E为圆心，EO为半径画弧，交CD于点G.由此探索S1·S2的值的变化情况.

图5

在Rt△BFK中，因为BK=8，BF=BO=10，

所以FK=6.

所以CF=CK-FK=4.

所以点F的坐标为F(4 ，8).

（2）如图5，设折痕与OC交于点L，那么EL垂直平分OG.

在Rt△EDG中，因为ED=8，EG=EO=17，

所以GD=15.

在Rt△CGL中，由CG=2，设LG=LO=n，

那么LC=8-n.

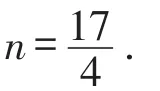
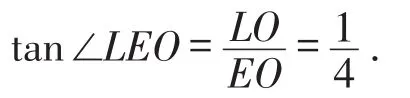
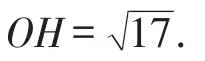
因为∠NGH与∠OMH都是∠MOG的余角，

所以∠NGH=∠OMH.

所以MH·NH=OH2=17.

【评析】第（2）小题中，由动点M在不同的位置，寻找不变的数量关系，通过特殊位置探索特殊关系，由探索的过程归纳出一般规律.根据题意结合特殊点确定S1·S2的值，采用大胆假设、小心求证是解决此题的关键，其中不受“点M从点E开始沿线段EH向点H运动，至与点N重合时停止”的约束，使解题摆脱了思维定式.

四、存在性开放探究题

存在性开放探究题一般是在确定的条件下判断某个数学对象是否存在的问题.这类问题中常常出现“是否存在”“是否有”“是否变化”等疑问句，以示结论有待判断.

解决这类问题的策略是先假设需要探索的对象存在，从条件和假设出发进行运算、推理，若出现矛盾，则否定存在；如果不出现矛盾，则肯定存在.

例4 若两条抛物线的顶点相同，则称它们为友好抛物线，抛物线C1：y1=-2x2+4x+2与C2：y2=-x2+mx+n为友好抛物线.

（1）求抛物线C2的解析式.

（2）点A是抛物线C2上在第一象限的动点，过点A作AQ⊥Ox，点Q为垂足，求AQ+OQ的最大值.

（3）设抛物线C2的顶点为C，点B的坐标为B( )-1，4，问在C2的对称轴上是否存在点M，使线段MB绕点M逆时针旋转90°得到线段MB′，且点B′恰好落在抛物线C2上？若存在，求出点M的坐标；若不存在，说明理由.

分析：（1）先求出y1的顶点坐标，然后根据友好抛物线的意义，利用两条抛物线的顶点坐标相同求m，n的值；

（2）根据（1）中求出的抛物线解析式，设点A的坐标为A(a，-a2+2a+3)，则OQ=a，AQ=-a2+2a+3.可得OQ+AQ与a的函数关系式，然后借助配方法求出OQ+AQ的最值；

（3）假设存在点M在C2的对称轴上，如图7，通过画图、作辅助线证明△BCM≌△MDB′.由全等三角形的性质可得BC=MD，CM=B′D.设点M的坐标为M( )

1，a，然后用含a的代数式表示点B′的坐标，将点B′的坐标代入抛物线的解析式即可求出a的值，从而得到点M的坐标.

（2）如图6，设点A的坐标为A(a，-a2+2a+3)，

因为OQ=a，AQ=-a2+2a+3，

图6

图7

（3）如图7，假设存在点M在C2的对称轴上，连接BM，作B′M⊥BM，且B′M=BM，连接BC，过点B′作B′D⊥CM，垂足为点D.

因为B(-1，4)，C(1 ， 4)，且抛物线的对称轴为x=1，

所以BC⊥CM，且BC=2.

因为 ∠BMB′=90°，所以 ∠BMC+ ∠B′MD=90°.

因为B′D⊥MC，所以 ∠MB′D+ ∠B′MD=90°.

所以∠MB′D=∠BMC.

所以△BCM≌△MDB′.

所以BC=MD，CM=B′D.

设点M的坐标为M(1 ，a)， 则B′D=CM=| 4-a|，MD=CB=2.

可得点B′的坐标为B′(a-3，a-2).

则-(a-3)2+2(a-3)+3=a-2.

整理，得a2-7a+10=0.

解得a=2或a=5.

当a=2时，M的坐标为M(1 ， 2 )；

当a=5时，M的坐标为M(1 ， 5).

综上所述，当点M的坐标为(1 ， 2)或(1 ， 5)时，点B′恰好落在抛物线C2上.

【评析】解决此类问题的常用方法是观察图形的特征，假设存在结论，通过演绎推理得出结论.而在解题过程中要注意分解知识点，注重问题的本质，如此题中已知函数解析式求坐标，已知坐标求函数解析式等，还要结合数形结合思想探索解题思路.

五、策略开放探究题

策略开放探究题的一般形式是题目的条件和结论是已知的或已知一部分，需要探究解题方法或设计解题方案.这类问题，在考试中一般以阅读理解题、作图题或应用题的形式存在.

解题策略是通过模仿、类比、试验、创新，综合运用所学知识，合理转化，建立数学模型，使问题得到解决.

例5为解决中小学大额班问题，某市各县区今年将改扩建部分中小学.某县计划对A，B两类学校进行改扩建，根据预算，改扩建2所A类学校和3所B类学校共需资金7 800万元，改扩建3所A类学校和1所B类学校共需资金5 400万元.

（1）改扩建1所A类学校和1所B类学校分别需要的资金是多少？

（2）该县计划改扩建A，B两类学校共10所，改扩建资金由国家财政和地方财政共同承担，若国家财政拨付资金不超过11 800万元，地方财政投入资金不少于4 000万元，其中地方财政投入到A，B两类学校的改扩建资金分别为每所300万元和500万元，试问共有哪几种改扩建方案？

分析：（1）根据题意列方程组解决；

（2）根据题意，设A类学校有a所，则B类学校有( )

10-a所，列出不等式组，确定a的取值范围，由此可得改扩建方案的所有可能，然后给出结果.

解：（1）设改扩建1所A类学校和1所B类学校所需资金分别为x万元和y万元，

答：改扩建1所A类学校需资金1 200万元，改扩建1所B类学校需资金1 800万元.

（2）设A类学校有a所，则B类学校有(10-a)所.

根据题意，得

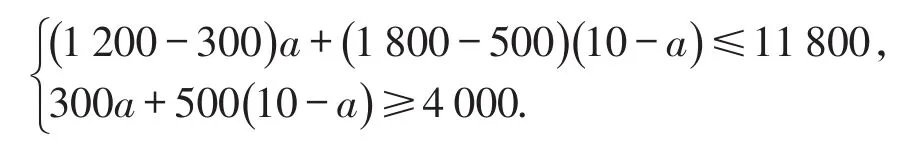
解得3≤a≤5，即a的取值为3或4或5.

所以共有以下3种改扩建方案.

方案1：A类学校有3所，B类学校有7所；

方案2：A类学校有4所，B类学校有6所；

方案3：A类学校有5所，B类学校有5所.

【评析】这类问题要根据题意建立数学模型，将复杂问题条理化，使解题思路清晰，过程简洁.对于代数问题，根据条件列出变量满足的方程或不等式（组），解方程或不等式（组），再根据要求给出答案；几何问题往往利用方程、不等式、三角函数和函数等知识，利用数形结合解决问题.

六、综合开放探究题

综合开放探究题的特征是条件、结论、解题方法都不全或未知，仅提供问题情境，需要补充条件，寻找结论，设计方法.

解决这类问题，一般是从基础知识和基本技能入手，多角度、多层次地分析问题的特点，着力探究一因多果和一果多因，探索问题成立所必须具备的条件，或特定的条件所得到的结论，再加以解答.

例6实验探究：（1）如图8（1），对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平，再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到线段BN，MN.观察图8（1），猜想∠MBN的度数是多少？并证明你的结论.

（2）将图8（1）中的三角形纸片BMN剪下，如图8（2）所示，折叠该纸片，探究MN与BM的数量关系.写出折叠方案，并结合方案证明你的结论.

图8

分析：（1）由图形的特点，连接AN（如图9）.根据折叠的性质，可知△ABN是等边三角形，再由∠NBM，∠ABM，∠ABN之间的关系解决问题；

（2）由于△BMN是直角三角形，由此折叠三角形纸片BMN，使点N落在BM上（如图10），探究△PBM的形状，寻找MN与BM的关系.

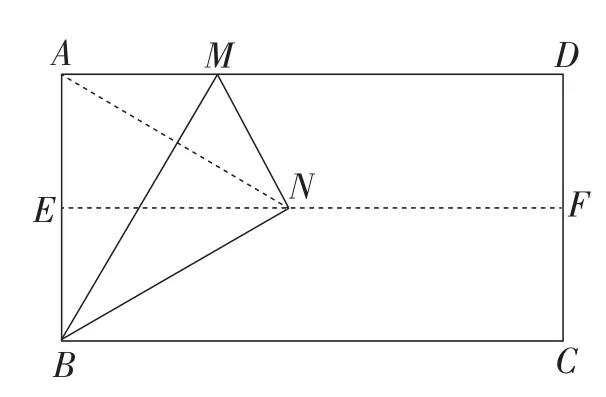
图9

图10

解：（1） ∠MBN=30°.理由如下.

如图9，连接AN.

因为直线EF是AB的垂直平分线，点N在EF上，所以AN=BN.

由折叠可知BN=AB.

所以△ABN是等边三角形.所以∠ABN=60°.

折叠方案：如图10，折叠三角形纸片BMN，使点N落在BM上，并使折痕经过点M，得到折痕MP，同时得到线段PO.

理由：由折叠可知MN=OM，∠MOP=∠MNP=90°.

所以△MBP是等腰三角形.

【评析】综合开放探究题难度较大，对学生的思维能力要求高，可培养学生的创新能力.对于有多重的结论开放的问题，应抓住条件中那些影响结论的因素，或分类讨论，或构造不同图形，全面考虑问题的各个方面，找到正确结果；对于只给出一个特定情境，而问题的条件、结论及推理判断过程均不确定的开放性问题，就要考虑相近或相似的题型、结论、方法，进行类比，梳理解题思路，寻找解题方法，从而使问题得到解决.

解开放探究题要认真审题，确定目标；更要深刻理解题意，开阔思路，发散思维，通过采用数形结合的方式，合理转化问题.解题过程就是合理地转化问题的过程，而直观归纳与严格推理论证相结合是处理这类问题的基本思路和解题策略.