2018年中考“综合与实践”专题解题分析
2019-06-20
(江西省教育厅教学教材研究室;江西省赣州市赣州中学)
一、内容要求分析
《义务教育数学课程标准(2011年版)》(以下简称《标准》)在课程内容部分指出,综合与实践是一类以问题为载体、以学生自主参与为主的学习活动.在学习活动中,要求学生综合运用“数与代数”“图形与几何”“统计与概率”等知识、方法和基本活动经验解决综合与实践问题.
二、主要特点分析
为有效落实《标准》的基本理念,更好地发挥中考试题对“综合与实践”领域教学的导向作用,综观2018年中考“综合与实践”类试题的呈现形式、考查内容基本趋于稳定,考查题型多样化.命题者在深入理解《标准》对“综合与实践”内容要求的基础上,力求在试题的考查内涵上不断创新,以问题为载体,注重对试题的综合性、过程性和应用性的考查.
1.综合性
综合性体现在以下三个方面:数学内部知识的综合,数学与其他学科的综合,数学与生活实际的综合.一般考查“综合与实践”的试题贯穿了一个较完整的综合活动的背景,问题的设置也产生于活动过程中.
(1)数学内部知识的综合.
例1(江苏·泰州卷)对给定的一张矩形纸片ABCD进行如下操作:先沿CE折叠,使点B落在CD边上(如图1(1)),再沿CH折叠,这时发现点E恰好与点D重合(如图1(2)).
(2)将该矩形纸片展开.
①如图1(3),折叠该矩形纸片,使点C与点H重合,折痕与AB相交于点P,再将该矩形纸片展开.求证:∠CPH=90°.
②不借助工具,利用图1(4)探索一种新的折叠方法,找出与图1(3)中位置相同的点P,要求只有一条折痕,且点P在折痕上,试简要说明折叠方法(不用说明理由).

图1

(2)①(方法1)如图2,连接EH.由翻折可得PH=PC,即PH2=PC2.根据勾股定理可得AH2+AP2=BP2+BC2.进而得出AP=BC.再根据PH=PC,∠A=∠B,得到Rt△PAH≌ Rt△CBP(HL). 进而得到∠HPC=90°.
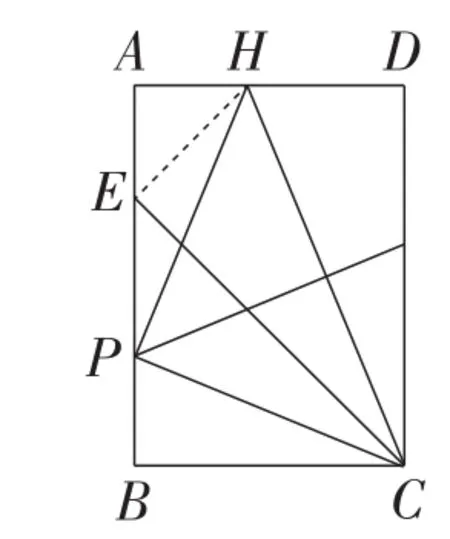
图2

图3
(方法2)如图3,连接EH,ED,设过点P的折痕交CD于点Q,连接HQ.由折叠的性质可得△AEH和△DHQ为等腰直角三角形,所以AH=AE,DH=DQ.又由折叠知DE⊥CH,PQ⊥CH,所以DE∥PQ.又因为AB∥CD,所以四边形PQDE是平行四边形.所以PE=DQ=DH.所以AP=AD=BC.又因为PH=PC,∠A=∠B=90°,所以Rt△PAH≌ Rt△CBP(HL),进而可得∠HPC=90°.
②(方法1)如图4,将矩形ABCD沿过点C的直线折叠,使点B的对应点B′落在CE上,则折痕与AB的交点即为点P.

图4
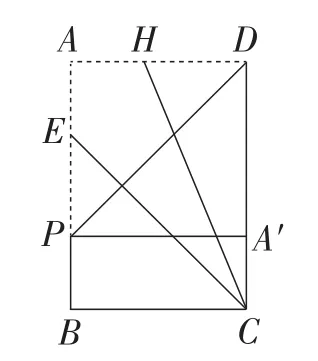
图5
(方法2)如图5,将矩形ABCD沿过点D的直线折叠,使点A的对应点A′落在DC上,则折痕与AB的交点即为点P.
【评析】此题创设了图形折叠的数学活动过程,并对实践操作过程中自然生成的问题进行设问,综合考查了等腰直角三角形的性质、矩形的性质、全等三角形的判定与性质,体现了对数学内部知识的综合考查.
(2)数学与其他学科知识的综合.
例2(四川·达州卷)如图6,在物理课上,老师将挂在弹簧测力计下端的铁块浸没于水中,然后缓慢匀速向上提起,直至铁块完全露出水面一定高度,则能反映弹簧测力计的读数y(单位:N)与铁块被提起的高度x(单位:cm)之间的函数关系的大致图象是( ).

图6

答案:D.
【评析】此题以物理现象为背景创设问题情境,由铁块从水中匀速上移逐渐移出水面直至停留在空中的过程,考虑到水的浮力影响,弹簧秤的读数由“保持不变—逐渐增大—保持不变”,故选D.此题考查了学生综合运用物理学知识、数学中的函数关系,以及函数图象来分析问题、解决问题的能力,体现了数学与其他学科知识的综合.
(3)数学与生活实际的综合.
例3(浙江·嘉兴卷)如图7(1),滑动调节式遮阳伞的立柱AC垂直于地面AB,点P为立柱上的滑动调节点,伞体的截面示意图为△PDE,F为PD的中点,AC=2.8 m,PD=2 m,CF=1 m,∠DPE=20°,当点P位于初始位置P0时,点D与点C重合(如图7(2)).根据生活经验,当太阳光线与PE垂直时,遮阳效果最佳.
(1)上午10:00时,太阳光线与地面的夹角为65°(如图7(3)),为使遮阳效果最佳,点P需从点P0上调多少距离?(结果精确到0.1 m)
(2)中午12:00时,太阳光线与地面垂直(如图7(4)),为使遮阳效果最佳,点P在(1)的基础上还需上调多少距离?(结果精确到0.1m)

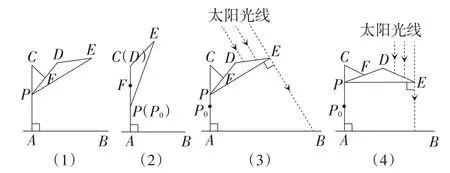
图7
答案:(1)为使遮阳效果最佳,点P需从P0上调0.6 m;
(2)点P在(1)的基础上还需上调0.7 m.
【评析】此题创设了实际测量的问题情境,考查了学生对实际情境的数学化抽象过程,以及构建解直角三角形,用锐角三角函数解决问题的能力,体现了数学与实际生活的综合.
2.过程性
“综合与实践”内容要求关注学生经历活动的整个过程,积累数学活动经验.这部分试题力求创设实践活动的完整过程,在学生经历观察、思考、归纳、类比、猜想、证明等一系列思维活动并解决问题的过程中,达到考查学生的数学综合素养,并形成基本活动经验的目的.

列表:
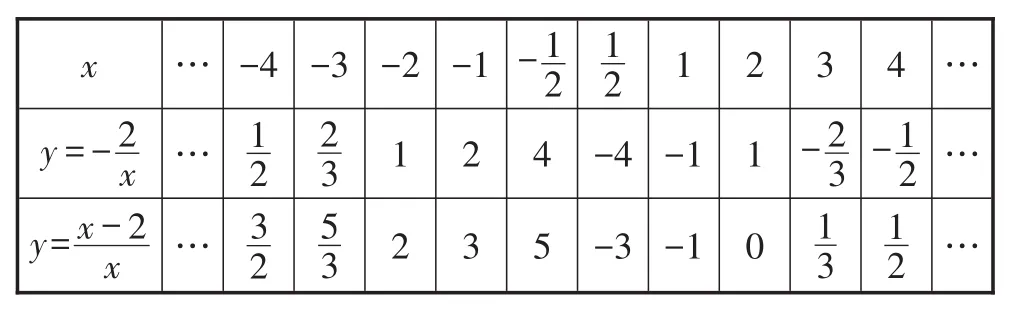
x -1--3 1 12 3 -2x 23 y=-x-2 x………32-2-4 12 1 2 2 3 53 1 2 4 5 1 2 -4 y=-1-1-3 2 1 0 23 4 -13 12………
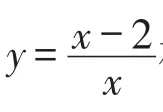
(1)试把y轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来;
(2)观察图象并分析表格,回答下列问题:
①当x<0时,y随x的增大而______;(填“增大”或“减小”)
③图象关于点_______中心对称.(填点的坐标)


图8

图9
答案:(1)所画函数图象如图9所示.
(2)①当x<0时,y随x的增大而增大;
③图象关于点(0 ,1)中心对称.
(3)因为x1+x2=0,所以x1=-x2.
所以A(x1,y1) ,B(x2,y2)关于点(0 ,1)对称.
所以y1+y2=2.所以y1+y2+3=5.
【评析】此题是一道综合考查反比例函数的图象与性质的解答题,试题设计有新意.此题呈现了一个学习活动的完整过程,让学生在答题过程中不自觉地经历由观察自变量取值范围,列表、描点、画图,观察图象,发现图象的性质,并利用性质解决数学问题,体现了对基本活动经验的考查.
例5(河南卷)(1)问题发现:
如图10(1),在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.
②∠AMB的度数为________.
(2)类比探究:

(3)拓展延伸:
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=7,试直接写出当点C与点M重合时AC的长.

图10
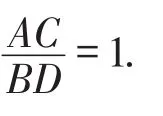
②由△COA≌△DOB,得∠CAO=∠DBO.根据三角形的内角和定理得∠AMB=180°-(∠DBO+∠OAB+∠ABD)=180°-140°=40°.


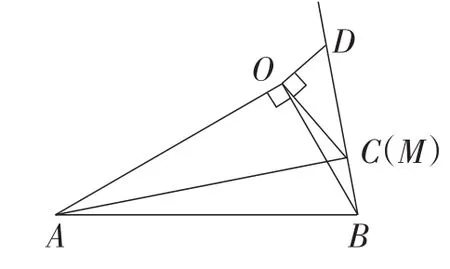
图11
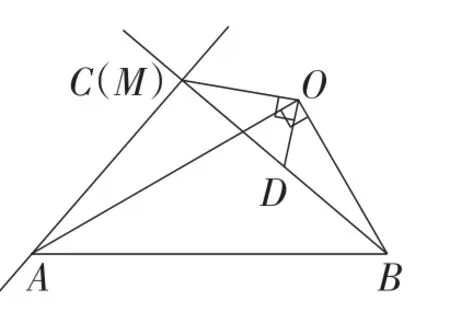
图12
【评析】此题呈现了数学活动中“发现问题—类比探究—拓展延伸”的完整过程,体现了从特殊到一般的探究思路,综合考查了几何变换,以及相似三角形、全等三角形的判定和性质,体现了对学生的分析推理能力、分类讨论思想、数形结合思想的考查.
3.应用性
综合与实践作为数学课程的一个重要领域,并不是在其他领域之外增加新的知识,而是强调数学知识的现实性和整体性.具体地说,综合与实践是指数学与外部世界的联系,数学内容之间的内在联系,以及数学在分析和解决问题过程中的综合应用.综合与实践的总体要求是帮助学生综合运用已有的知识和经验,经过自主探究和合作交流,解决与生活经验密切联系的、具有一定综合性和挑战性的问题,以发展学生解决问题的能力.
例6(浙江·绍兴卷)实验室里有一个水平放置的长方体容器,从内部量得它的高是15 cm,底面的长是30 cm,宽是20 cm,容器内的水深为xcm.现往容器内放入如图13所示的长方体实心铁块(铁块一面平放在容器底面),过顶点A的三条棱的长分别为10cm,10cm,ycm(y≤15),当铁块的顶部高出水面2 cm时,x,y满足的关系式是_______.

图13
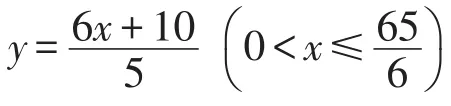


图14
(1)求k,并用t表示h;
(2)设v=5,用t表示点M的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围),及y=13时运动员与正下方滑道的竖直距离;
(3)若运动员甲、乙同时从A处飞出,速度分别是5米/秒、v乙米/秒.当甲距x轴1.8米,且乙位于甲右侧超过4.5米的位置时,直接写出t的值及v乙的范围.
答案:(1)h=5t2;
(2)10(米);
(3)t=1.8,v乙> 7.5.
例8(陕西卷)问题提出
(1)如图15(1),在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为_______.
问题探究
(2)如图15(2),⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值.
问题解决
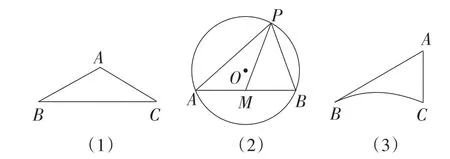
图15
解析:(1)如图16,设△ABC的外接圆圆心为点O,连接OA,OB,OC,经过计算可得R=AB=AC=5.



图16

图17
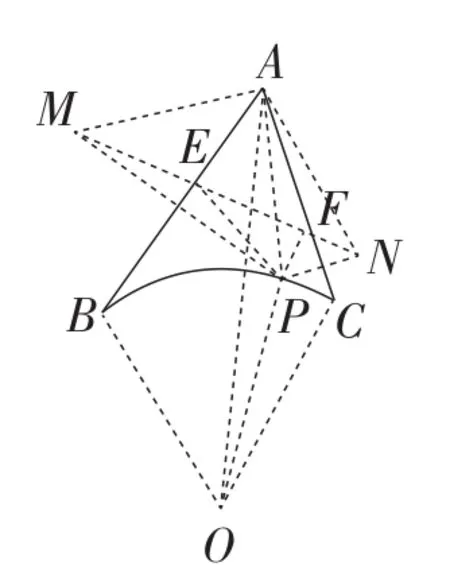
图18
【评析】以上三道题均要求学生综合运用已有的知识和经验,经过自主探索和合作交流,解决与生活经验密切联系的、具有一定挑战性和综合性的问题.例6考查了数学几何体与物理学中容积的综合应用;例7考查了反比例函数、二次函数与物理学运动的综合应用;例8考查了几何知识与实际生活中路线最短规划的综合应用,凸显了2018年中考试题中“综合与实践”内容的应用性特点,有效地提高了学生的数学应用意识与创新意识.
三、解题思路评析
1.以逻辑推理为主线,利用分类讨论思想解题
例9(浙江·嘉兴卷)如图19,在矩形ABCD中,AB=4,AD=2,点E在CD上,DE=1,点F是边AB上一动点,以EF为斜边作Rt△EFP.若点P在矩形ABCD的边上,且这样的直角三角形恰好有两个,则AF的值是_______.

图19

【评析】此题考查了学生对矩形的性质、勾股定理、三角形中位线定理、圆的性质的综合运用能力.试题综合性较强,对学生的逻辑推理能力有较高要求,具有一定难度.解题时需要合理运用分类讨论进行有条理的逻辑推理.
2.以直观想象为导向,利用数形结合思想解题
例10(浙江·嘉兴卷)已知,点M为二次函数y=-(x-b)2+4b+1图象的顶点,直线y=mx+5分别交x轴正半轴,y轴于点A,B.
(1)判断顶点M是否在直线y=4x+1上,并说明理由.
(2)如图20(1),若二次函数图象也经过点A,B,且mx+5>-(x-b)2+4b+1,根据图象,写出x的取值范围.


图20
解析:(1)根据顶点式解析式,可得顶点坐标,将点的坐标代入函数解析式进行检验,可得点M在直线y=4x+1上;
(2)根据待定系数法,可得二次函数的解析式.根据函数图象与不等式的关系,可知图象在下方的函数值小,可得x<0或x>5;
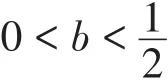
【评析】此题是一道二次函数的综合题.解第(1)小题的关键是把点的坐标代入函数解析式,并进行检验;解第(2)小题的关键是利用函数图象与不等式的关系求解;解第(3)小题的关键是解方程组,得出顶点M的纵坐标的取值范围,又利用二次函数的性质,得到当a<0时,点与对称轴的距离越小函数值越大.其中借助图象来解决问题起着直观的导向作用,可见数形结合思想在解题中具有重要地位.
3.以数学运算为支撑,利用特殊到一般思想解题
例11(山东·青岛卷)问题提出:用若干相同的一个单位长度的细直木棒,按照如图21所示的方式搭建一个长方体框架,探究所用木棒条数的规律.

图21
问题探究:我们先从简单的问题开始探究,从中找出解决问题的方法.
探究1
用若干木棒来搭建横长是m,纵长是n的矩形框架(m,n是正整数),需要木棒的条数如下.
如图22,当m=1,n=1时,横放木棒为1×(1 +1)条,纵放木棒为(1 +1)×1条,共需4条;
如图23,当m=2,n=1时,横放木棒为2×(1 +1)条,纵放木棒为(2 +1)×1条,共需7条;
如图24,当m=2,n=2时,横放木棒为2×(2 +1)条,纵放木棒为(2 +1)×2条,共需12条;
如图25,当m=3,n=1时,横放木棒为3×(1 +1)条,纵放木棒为(3 +1)×1条,共需10条;
如图26,当m=3,n=2时,横放木棒为3×(2 +1)条,纵放木棒为(3 +1)×2条,共需17条.

图22
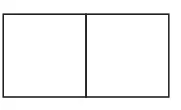
图23
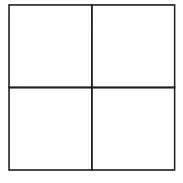
图24
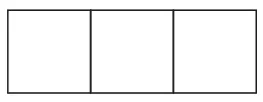
图25

图26
问题1:当m=4,n=2时,共需木棒的条数为___.
问题2:当矩形框架横长是m,纵长是n时,横放的木棒的条数为______,纵放的木棒的条数为______.
探究2
用若干木棒来搭建横长是m,纵长是n,高是s的长方体框架(m,n,s是正整数),需要木棒的条数如下.
如图27,当m=3,n=2,s=1时,横放与纵放木棒之和为[3 ×(2 +1)+(3 +1)×2]×(1 +1)=34条,竖放木棒为(3 +1)×(2 +1)×1=12条,共需46条;
如图28,当m=3,n=2,s=2时,横放与纵放木棒之和为[3 ×(2 +1)+(3 +1)×2]×(2 +1)=51条,竖放木棒为(3 +1)×(2 +1)×2=24条,共需75条;
如图29,当m=3,n=2,s=3时,横放与纵放木棒之和为[3 ×(2 +1)+(3 +1)×2]×(3 +1)=68条,竖放木棒为(3 +1)×(2 +1)×3=36条,共需104条.
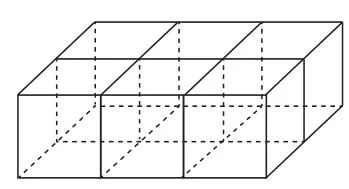
图27

图28
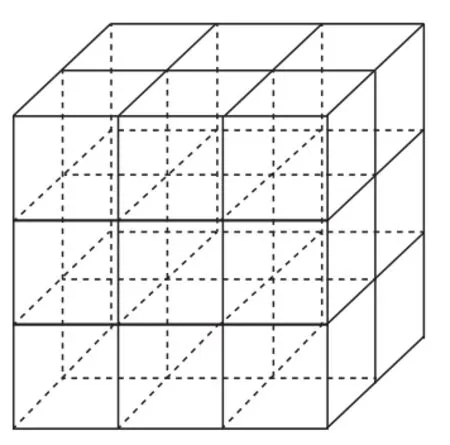
图29
问题3:当长方体框架的横长是m,纵长是n,高是s时,横放与纵放木棒条数之和为_______,竖放木棒条数为______.
实际应用:现在按探究2的搭建方式搭建一个纵长是2、高是4的长方体框架,总共使用了170条木棒,则这个长方体框架的横长是_______.
拓展应用:若按照如图30所示的方式搭建一个底面边长是10,高是5的正三棱柱框架,需要木棒的条数为______.
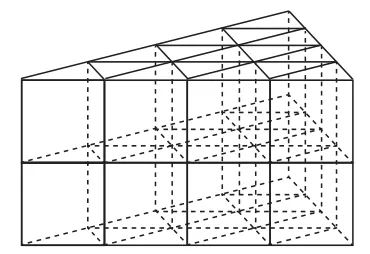
图30
解析:问题1:当m=4,n=2时,横放木棒为4×(2 +1)条,纵放木棒为(4 +1)×2条,共需22条;
问题2:当矩形框架横长是m,纵长是n时,横放的木棒为m(n+1)条,纵放的木棒为n(m+1)条;
问题3:当长方体框架的横长是m,纵长是n,高是s时,横放与纵放木棒条数之和为[m(n+1)+n(m+1)]·(s+1)条,竖放木棒(m+1)(n+1)s条.
实际应用:按探究2的搭建方式搭建一个纵长是2、高是4的长方体框架,总共使用了170条木棒,则这个长方体框架的横长是4.
拓展应用:若按照如图30所示的方式搭建一个底面边长是10,高是5的正三棱柱框架,横放与纵放木棒条数之和为1 320条.
【评析】此题是一道考查图形的变化规律问题.解题的关键是理解题意,运用从特殊的例子中总结归纳出一般的内在规律,然后利用这个规律去验证与解决同类的数学问题.在这个探究与解决问题的过程中,数学运算能力一直起到了重要的支撑作用.
4.以数学建模为过程,利用类比、转化或化归思想解题
例12(山东·淄博卷)(1)操作发现:
如图31(1),小明画了一个等腰三角形ABC,其中AB=AC,在△ABC的外侧分别以AB,AC为腰作了两个等腰直角三角形ABD,ACE,分别取BD,CE,BC的中点M,N,G,连接GM,GN.小明发现了:线段GM与GN的数量关系是_______,位置关系是_______.
(2)类比思考:
如图31(2),小明在此基础上进行了深入思考.把等腰三角形ABC换为一般的锐角三角形,其中AB>AC,其他条件不变,小明发现的上述结论还成立吗?试说明理由.
(3)深入研究:
如图31(3),小明在(2)的基础上,又进行了进一步的探究.向△ABC的内侧分别作等腰直角三角形ABD,ACE,其他条件不变,试判断△GMN的形状,并给予证明.

图31
解析:(1)线段GM与GN的数量关系是GM=GN,位置关系是GM⊥GN.理由:如图32,连接DC,EB,利用SAS判断出△ACD≌△AEB,得出CD=BE,∠ADC=∠ABE,进而判断出∠BDC+∠DBH=90°,即∠BHD=90°,最后用三角形中位线定理即可得出结论.
(2)上述结论仍成立.如图33,连接DC,EB,同(1)的方法即可得出结论.
(3)如图34,连接DC,EB,并延长交于点H,同(1)的方法得出MG=NG,最后利用三角形中位线定理和等量代换即可得出结论.

图32

图33

图34
【评析】此题是一道有关三角形的综合题,主要考查等腰直角三角形的性质、全等三角形的判定和性质、平行线的判定和性质、三角形的中位线定理.解题的关键是正确作出辅助线,运用类比思想解决问题.在整个解题过程中,要求学生从特殊的例子入手,建立几何图形模型,然后利用这个模型解决变式问题.
例13(江苏·扬州卷)问题呈现
如图35,在边长为1的正方形网格中,连接格点D,N和E,C,DN和EC相交于点P,求tan∠CPN的值.
方法归纳
求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中∠CPN不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题,比如连接格点M,N,可得MN∥EC,则∠DNM=∠CPN,连接DM,那么∠CPN就变换到Rt△DMN中.
问题解决
(1)直接写出图35(1)中tan∠CPN的值为_______;
(2)如图35(2),在边长为1的正方形网格中,AN与CM相交于点P,求cos∠CPN的值;
思维拓展
(3)如图35(3),AB⊥BC,AB=4BC,点M在AB上,且AM=BC,延长CB到点N,使BN=2BC,连接AN交CM的延长线于点P,用上述方法构造网格求∠CPN的度数.
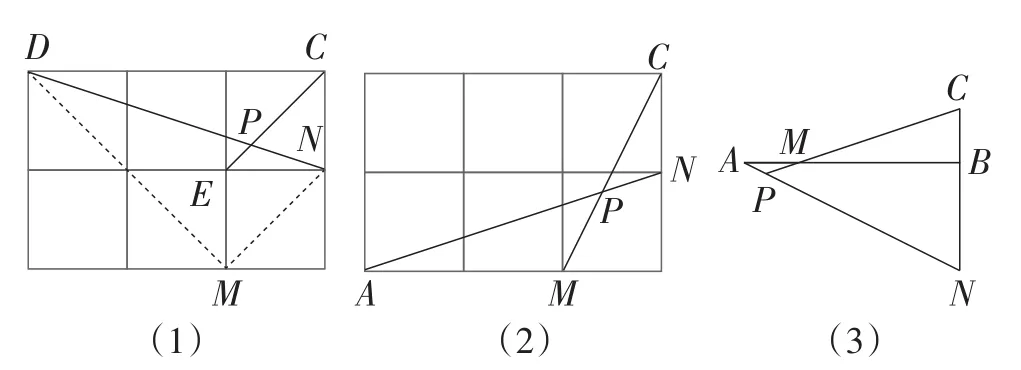
图35
解析:(1)2;
(2)如图36,取格点D,连接CD,DM.
因为CD∥AN,
所以∠CPN=∠DCM.
因为△DCM是等腰直角三角形,
所以∠DCM=∠D=45°.
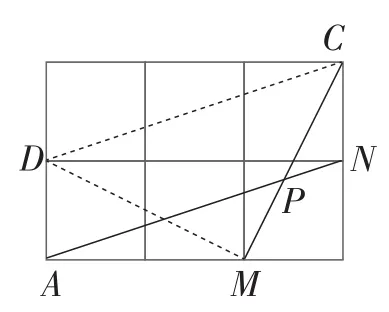
图36

图37
(3)如图37,取格点M,连接AN,MN.
因为PC∥MN,
所以∠CPN=∠ANM.
因为AM=MN,∠AMN=90°,
所以∠ANM=∠MAN=45°.
所以∠CPN=45°.
【评析】此题考查了三角形的性质、平行线的性质、勾股定理、直角三角形的判定和性质等知识.解题的关键是学会利用数形结合思想解决问题,学会运用转化思想思考问题,属于较难题.因此,从数学的视角发现问题、提出问题、分析问题、建立模型、求解结论、验证结果,最终解决实际问题的建模解题过程值得关注.
四、特色解法赏析
在2018年全国各地中考试题中对于“综合与实践”类问题都很重视,试题的设计符合《标准》的要求,同时又兼顾地域特色,倡导学生依据已有学习经验独立解决问题.试题解法丰富,且各具特色,由此彰显数学的和谐与统一.下面举例说明.
例14(湖南·常德卷)5个人围成一个圆圈做游戏,游戏的规则是:每个人心里都想好一个实数,并把自己想好的数如实地告诉与他相邻的两个人,然后每个人将与他相邻的两个人告诉他的数的平均数报出来,若报出来的数如图38所示,则报4的人心里想的数是________.

图38
解析:设报4的人心里想的数是x,则报1的人心里想的数是10-x,报3的人心里想的数是x-6,报5的人心里想的数是14-x,报2的人心里想的数是x-12,所以有x-12+x=2×3.解得x=9.故此题答案为9.
【赏析】此题属于阅读理解和探索规律题,考查的知识点有平均数的相关计算,以及对方程思想的运用.解决此题的方法有些特殊,题意理解起来比较容易,如果仅从数字去逐个推理,比较繁杂,不容易理清思路,但是借助方程思想便能理清思路,从而解决问题.只需多设几个未知数,把题中的等量关系全部表示出来,再结合题意进行整合,问题即可解决.此题还可以根据报2的人心里想的数是6-x,从而列出方程x-12=6-x来求解.
例16(江西卷)如图39,在△ABC中,AB=8,BC=4,AC=6,CD∥AB,BD是∠ABC的平分线,BD交AC于点E,求AE的长.

图39
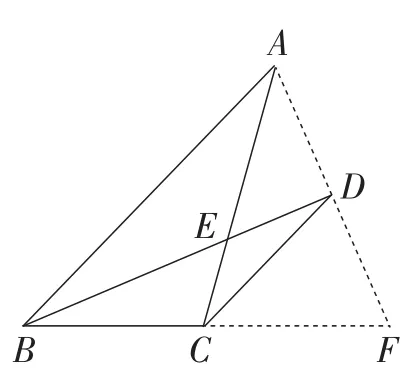
图40
解析:(方法1)如图39,首先证明△ABE∽△CDE,然后求出AE与CE的比,进而求出AE的长;
(方法2)如图40,将AB沿BD向下翻折得FB,可知点F落在BC延长线上,连接AF,可证得点E是△ABF的重心,从而得AE与CE的比为2∶1.所以AE=4.
【赏析】方法1是利用平行的条件联想到三角形相似,从而求出线段的长;方法2是由中点与角平分线联想到补全图形,从而得出新的图形,再把握其特征,得出点E是△ABF的重心,进而求解.由此可以看出,解题时充分运用图形变换,“静”中生“动”,往往能事半功倍.
例17(广东·广州卷)如图41,在四边形ABCD中,∠B=60°,∠D=30°,AB=BC.
(1)求∠A+∠C的度数;
(2)连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由.
(3)若AB=1,点E在四边形ABCD内部运动,且满足AE2=BE2+CE2,求点E运动路径的长度.
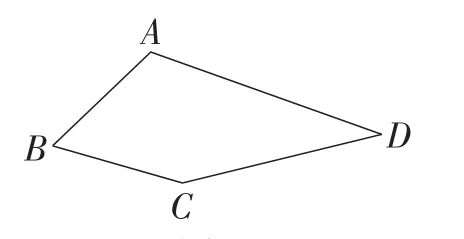
图41
解析:(1)利用四边形内角和定理计算即可.
(2)如图42,连接BD,以BD为边向下作等边三角形BDQ,证明△DCQ是直角三角形,即可解决问题.
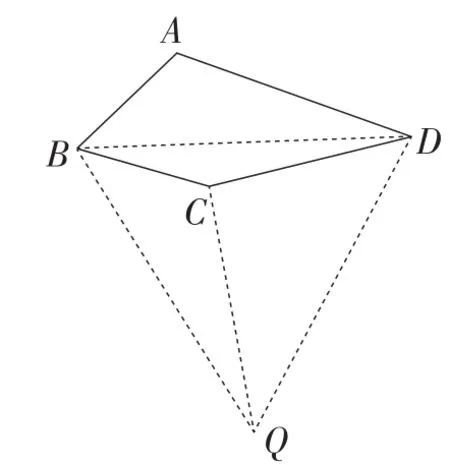
图42

图43
【赏析】此题考查了四边形的性质、等边三角形的判定和性质、勾股定理及其逆定理、弧长公式等知识,解题关键是构造全等三角形.此题属于中考压轴题,其中由条件AE2=BE2+CE2逆向联想构造辅助线是此题较鲜明的特色.
