让练习成为核心素养生根的沃土—基于核心素养下的练习优化策略

广东省东莞市东莞高级中学(523000)肖志军

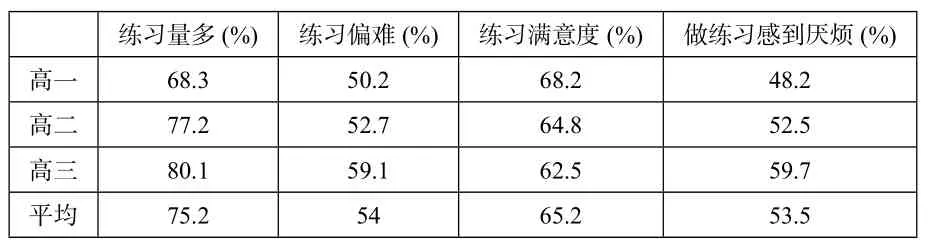
笔者受课题组委托，对本校三个年级不同层次的学生采取分层抽样，做了一个数学练习的问卷调查，选取了部分选项的统计结果，如下表：

?

从统计结果可以看出大多数学生(占75.2%)觉得练习量多，超过一半(占54.%)的学生认为练习偏难，同时做练习时感到厌烦，而且对数学练习的满意度也只有65.2%.当然，一次问卷调查的结果也不能说明全部事实，但从侧面反映出平时的数学练习形式单一，模式僵化且效率低下，机械重复训练较多，难度过大且练习量大，有些学生甚至不堪重负，挫伤了学生学习数学的积极性， 使不少学生对数学望而生畏，练习成了学生的“包袱”，由此产生了很大的厌学情绪，阻碍了学生能力和核心素养的形成，更加不可能使核心素养落地生根.

那么，在新课程理念下如何优化练习，使之更科学、更实效，并使之成为核心素养生根的沃土，笔者认为要遵循以下几个基本原则和策略：

1 立足课标和考纲，指向性强

练习设计可以千变万化，考察的角度、形式以及问题背景可以新，但对所考察的基础知识、基本技能、基本思想方法不能变.因为培养和发展“四基”、“四能”是学生核心素养形成的前提，是数学核心素养的价值取向的具体体现.

考纲对知识考察的要求由低到高分为三个层次，依次是知道(了解、模仿)、理解(独立操作)、掌握(运用、迁移)，且高一级的层次要求包括低一级的层次要求.所以在设计练习时，要对照课标和考纲要求，使练习更合理、更科学.比如说，《导数及其应用》这一章节中，考纲对复合函数要求是会求简单的复合函数(仅限于形如f(ax+b)的复合函数)的导数.而某校的一次月考题却出了一道这样的题：

(18年某校月考理7)函数y =(sin x2)3的导数是( )

A.y′=3x sin x2·sin 2x2B.y′=3(sin x2)2

C.y′=3(sin x2)2·cos x2D.y′=6 sin x2·cos x2

该题考察的是三层复合函数的导数，而且还夹杂着倍角公式的应用，平均分不到2 分，笔者认为该题背离了考纲要求，可能会将学生带入求导的“黑洞”.

2 注重基础，考虑学生的认知水平，紧扣教材理性拓展

数学核心素养不是凭空生成的，它起源于教材，并以教材为载体孕育和发展而来.所以教材应该是落实核心素养的主阵地，是高考命题的主要依据，因为教材才是通用的，才是稳定的.所以立足教材设计练习既保证了难度的稳定性，也能保证在稳定的基础上进行创新.同时，练习的设计不能只从教材和自己的经验出发，还需要考虑学生的思维水平，以学生现有的知识结构、主观经验为起点，充分估计学生会在何时何处有何疑难.只有在把握好学生认知和思维水平的前提下，对练习进行理性拓展才有意义，才会更科学.很多高考中常考而教材中却未有明确阐述的知识都可以通过练习的形式理性拓展而来.

3 突出主干，体现能力，有思维深度

数学是一门思维的学科， 是培养理性思维的重要载体，强调“以能力立意”，从问题入手，对客观事物中的数量关系和空间形式作出思维判断，能运用数学的思维分析问题，并运用数学知识解决问题，以此来考察学生的数学核心素养水平.而能力的考查包括数学抽象、模式构建、直观想象、逻辑推理、运算求解等诸方面，这些能力所涉及的数学知识都蕴含在主干知识当中，并且大多以主观题的形式出现，所以在练习的设计时，要突出主干知识对能力的考察要求，并要有一定的思维深度.

比如说，选修2-3《导数及其应用》的练习中，教材在32页的B 组练习设置了这样一道题，要求利用函数的单调性，证明下列不等式，并通过函数图像直观验证：

(1)sin x ＜x，x ∈(0,π);(2)ex＞1+x，x0;

(3)ln x ＜x ＜ex，x ＞0.

随着课程改革的不断深入，导数知识在高考中的考查要求也逐年加强，在历年的考题中，常考察ex与含x 多项式或ln x 与含x 多项式的混合型函数，由于导数是与大学衔接紧密的内容，灵活性高，综合性强，能比较全面的考查学生数形结合、分类整合、转化与化归、函数与方程等数学思想，是体现学生数学核心素养水平的最有效的载体.

4 注重通性通法，淡化特殊技巧

所谓的“通性通法”就是指有着普遍性的常规解题模式和常用的数学思想方法，是对数学知识最高层次的概括与提炼，近几年来一直是高考考查的核心.练习的设计，从方法层面，要注重通行通法，这也是落实核心素养的一个着力点，反对在花岗岩上盖茅房，也反对在沙滩上建高楼.因此高中数学新课程中，删减了以往那种繁琐的计算(或改为用计算器计算)，淡化了人为技巧化的难题，曾经那种追求试题难度或只讲求技巧的模式渐渐为新课标所抛弃，追求通性通法已经成为新课标的主流.

比如说，在设计与“函数”有关的练习时，应该围绕函数的性质及研究函数性质的基本思想方法，如数形结合、函数与方程、转化与化归、特殊到一般的思想方法进行练习设计.

再比如，圆锥曲线的考查经常围绕将直线方程与曲线方程联立，整理成一元二次方程，再利用判别式、韦达定理、距离公式等可以编制出大量的图形位置关系、最值(范围)、定点定值等问题，这些问题都考查了解析几何的基本思想方法，这种通性通法考察在高中数学的很多模块中也是很多见的.

5 关注应用，有所创新，培养数学抽象和数学建模素养

学会用数学的眼光发现和提出问题，发展数学抽象和数学建模素养，是数学核心素养最基本的要求.具体说来，就是能从数学的角度看问题，以良好的科学态度和创新精神，合理地提出新问题，并对问题进行“数学方式”的理性思维，善于对现实世界中的现象和过程进行合理的简化和量化，并在观察、分析和研究后， 借助数学模型来解决问题.如函数模型、数列模型、线性规划模型、空间特征几何体模型等，它们能概括地、集中地反映现实对象的某些特征，从而帮助人们迅速、有效地了解并掌握那个对象的本质.

比如， 最近几年的高考内容中增加了数学文化的要求.我国古代数学文化中有大量的实际问题，此类问题常结合函数、数列、空间几何体、算法等内容进行考察.

(2017 课标II 理3)我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯? ”意思是：一座7 层塔共挂了381 盏灯，且相邻两层中的下一层灯数是上一层灯数的2 倍，则塔的顶层共有灯( )

A.1 盏 B.3 盏 C.5 盏 D.9 盏

此题以传统数学文化为载体考查数学知识的实际应用，求解的关键是将古代实际问题抽象为数学问题，建立数列模型，运用数列知识建立方程求解.这类题的考查，增加了应用性和创新性的要求，充分发挥考题的育人功能和积极的导向作用，既弘扬了中华优秀传统文化，也能积极培育和践行核心价值观，是数学核心素养的具体体现.

总之，数学练习是课堂教学的延续和补充，是学生学习效果评价的重要环节.随着新课程的不断深入推进，切实履行好给学生减负的责任要求，科学设计练习，整合优化练习显得越来越重要.教师只有明确优化练习的基本原则和策略，才有可能让练习发挥积极的导向作用，才能使练习真正成为核心素养生根的沃土.