培养学生数学核心素养，强化数学思想教学

广东省佛山市南海区大沥镇盐步第三初级中学(528247)胡玉娴

数学核心素养通过数学的基础知识和基本能力来实现，数学思想与数学核心素养密切相关.在研究数学学科中不可缺少的思想是数学思想，数学思想是学习数学、理解和掌握数学的追求.在初中阶段，渗透和强化数学思想，对学生的数学核心素养养成非常重要.下面笔者以具体内容为载体，谈谈如何强化数学思想教学，帮助学生学会思考、提升认知水平和领悟数学的真谛，从而达成学生数学核心素养养成目标.

一.数形结合阐释知识，强化数形结合思想

著名数学家华罗庚说过“数无形，少直观，形无数，难入微”.“以数想形，以形助数”.是以数为手段形为目的，借助数的精确性和规范严密性来阐明形的某些属性;或者是以形为手段数为目的，借助形的生动性和直观性来阐明数之间的联系.如此就能使复杂问题简单化，抽象问题具体化，能够变抽象思维为形象思维，有助于把握数学问题的本质，使数学的规律性与灵活性有机结合.

例如，矩形纸片的折叠问题中，有这样典型的问题：已知，如图1，在矩形ABCD 中，已知AB =6cm，BC =10cm，折叠矩形的一边AD，使点D 落在BC 边上的点P 处，折痕为AE，(1)求CE 的长;(2)若设BP 为x，CE 为y，试确定y 与x 的函数解析式，当x 取何值时，y 的值最大? 最大值是多少?

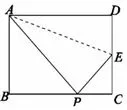
图1

本题看似是几何图形题， 实质是利用图形告知条件， 用代数运算方式计算出结果.第一问， 由折叠可得AD = AP = 10，DE = DP，∠DAE = ∠EAP.设DE = a， 则CE = 6-a，EP = a，根据勾股定理， 由△ABP 是直角三角形， 可得则CP = 2，由△CEP 是直角三角形，可得CP2+CE2=EP2， 则有22+ (6 - a)2= a2， 解得故CE =第 二 问， 由∠APE = ∠D = 90°， 可 得Rt△ABP ～Rt△PCE， 从而即解得所以x = 4 时，y有最大值，最大值是借助数的精确性和规范严密性，阐明了三角形的全等与相似的性质.又如，实数a、b 在数轴上的位置如图2 所示，求的化简结果.

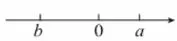
图2

此题若不参考数轴，对二次根式化简不了.由数轴可得b ＜0 ＜a,|b| ＞|a|， 所以a+b ＜0， 故|a+b|+a=-a-b+a=-b.

二次根式的性质与化简应用到了实数与数轴的关系，典型的数形结合.一个简单的图形，让问题的条件清晰，从而可迅速解答问题.

培养学生建立图形的意识，是数形结合思想方法的前提和基础.面对一些抽象复杂的数学问题，不能仅盯着文字，还要一边阅读文字条件一边将相应的图形画出来.画图的过程中已经是在帮助读题者理清思路，从中发现问题解答的切入点.通过数形结合思想，学生的抽象思维能力与逻辑思维能力得到训练和提升.

二.迁移知识难点，强化化归转化思想

有些数学问题的解答，并不是进行观察或对题目的已知条件直接利用就能分析解决.“他山之石可以攻玉”，许多时候，我们需要对问题的条件做一定的转化后，归结到一类比较容易解决的问题， 如化未知为已知、化繁为简， 化难为易，或者通过将问题向与其相似的内容进行变换，用此相似内容的成功分析来完成当前问题的解答，从而最终得解.

例如， 在四边形的内容教学中， 有这样一个问题：如图3 所示， 在等腰梯形ABCD 中，AD//BC， AC⊥BD， AD = 3，BC =7，求梯形的面积.

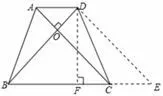
图3

对题目的问题直接进行分析， 已知条件不充分.于是，引导学生过点D 作DE//AC 交BC 的延长线于点E， 作DF⊥BC 于F，由此得四边形ADEC 是平行四边形，得出AD = CE， AC = DE 的结论， 又从梯形ABCD 是等腰梯形，得到AC = DE = BD，又由AC⊥BD 得BD⊥DE，△BDE 是等腰直角三角形根据梯形面积计算公式，答案顺利可得.结果得出后，与学生一起分析整个思维过程：由已知条件等腰梯形对角线互相垂直，通过平移对角线将等腰梯形转化为平行四边形和等腰直角三角形，使问题得到解决.这集中体现了数学的转化思想，学生从中体验到了转化对问题分析有重要的促进作用.

结合教学要求，灵活利用化归转化思想的特点，把新知识转化为已知知识，把一般转化为特殊的解决问题的思路和方法，能让学生轻松有效地深入掌握和运用转化的数学思想，走出固定的思维，积极开发空间想象能力，综合发展思维和实践应用能力.向学生渗透化归转化思想，培养学生运用转化思想的能力，充分发挥转化思想方法的作用，是提高学生的综合素质，提升学生数学学科核心素养所必需的.

三.分类讨论不重不漏，强化分类思想

初中阶段，分类讨论思想在数学题中经常出现.学生在做题时常犯的错误之一就是不会对问题进行分类讨论或者讨论不全，再不然就是讨论全了结果不一定对，结果就掉进了出题老师挖的坑里.

例如，解不等式(a+1)x ＜a2-1，这个问题看似简单，如果没有讨论a+1 的正负情况，不加思考去做，就会得出x ＜a-1 的结果，这个答案显然是不全面的，是错误的.因为当a+1 ＞0 时，不等式左右两端可以同时除以a+1，答案就是x ＜a-1;如果当a+1 = 0 时，不等式左右两端可以同时除以0，x 无解;当a+1 ＜0 时，不等式左右两端可以同时除以a+1，不等式的符号要变号，答案就是x ＞a-1.只有通过分类讨论后，得到的结论才是完整的、正确的，如不分类讨论，就容易遗漏条件导致结果错误.

不难发现，在几何图形的点和线出现有不同位置的情况，要逐一讨论求解.涉及代数式或函数或方程中，根据字母的不同取值情况， 也需要在不同的取值范围内讨论解决问题.通过分类讨论可帮助学生进行概括、总结出规律性的知识，使一些错综复杂的问题变得简单，解题思路变得清晰，解题步骤变得明了.从而加强了学生思维的条理性和缜密性，培养了逻辑思维能力，提高学生的数学学习能力.

四.方程灵活解问题，强化方程思想

中学数学的一些几何题目蕴含了图形数量上的相等关系，根据分析这些相等关系，合理设出未知数，用未知量表示已知量的方法，建立方程，使原问题得到解决.通过方程把几何与代数内容有机结合，这就是方程思想，是应用方程思想解决非方程问题的极富创造力的一个方面.

例如，在等腰三角形的性质内容的教学过程中，出现了这样一道习题：等腰三角形一腰上的中线把周长分为15 和12两部分，求该三角形各边的长.

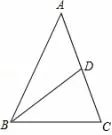
图4

如何求此等腰三角形各边的长? 由图形及已知条件直接求解显然不行.由题意知，等腰三角形的一腰上的中线把这个三角形的周长分为12 和15 两部分，由于没有具体说明哪部分是12， 哪部分是15; 所以需分两种情况进行分析：第一种情况：AB +AD = 12， 第二种情况：AB+AD = 15;由此可分别求得三角形的三边的长.在△ABC 中， AB = AC， BD 是中线， 设AB = x， BC = y.情况一：当AB +AD = 12 时， 则解得所以三角形三边的长分别为8、8、11;情况二：当AB+AD =15 时，则解得所以三角形三边的长分别为10、10、7，经检验，两种情况均符合三角形三边关系定理，因此这个三角形的三边长分别为8,8,11 或10,10,7.虽然从表面看来，这是以几何中等腰三角形性质为背景的数学问题，但是在解答过程中，所依靠的仍然是方程的思想.学生也因此感受到方程思想的巧妙，从而建立起运用方程思想分析问题的思维意识.

方程思想就是从问题的数量关系入手，运用数学语言将问题的条件转化为数学模型—-方程或方程组，或者运用方程的性质去分析、转化问题，最终解决问题.方程思想的巧妙运用，使学生的解题思维清晰、灵活.学生不用拘泥于某一知识方法中，而是可以借助方程思想来加以分析，无疑是为高效学习数学知识多了一条捷径.

五.整体思考解问题，强化整体思想

“只见树木、不见森林”的思考方法，是在解题时，很多学生的习惯方法.习惯于从问题的局部出发，将问题分解成若干个简单的子问题，然后再各个击破、分而治之，这是一种常见的有效的方法.但还有许多的数学问题，用这种方法，却常常会导致解题过程繁杂、运算量大，甚至半途而废.转换一下角度，如果我们在研究和解决问题时从问题的整体出发，突出对问题整体结构的分析、判断，发现问题的整体结构特征和逻辑关系，善于用“识大体，顾大局”的理念，把某些式子或图形看成一个整体，把握它们之间内在的联系，确定解决问题的思路、方法、途径，找到最合理，最简捷实用的解题方法，使问题化难为易，化繁为简，提高解题效率，这种思考问题的思维方法就是通常所说的整体思想..

例如，在一次练习中有这样一个问题：已知关于x、y 的二元一次方程组的解为那么求关于x、y 的二元一次方程组的解.学生很自然地就把代入解出a、b 的值，再代入进行求解，这种解法步骤是可行的，但是计算量很大，比较繁琐.如果采用整体思想，在方程组中，设则此时方程组变形为由第一个方程组可知从而得第二个方程组的解为通过整体加减避免了求复杂的未知数的值，又简化了方程组，解答直接简便.

一些数学问题，如果从局部入手，难以各个突破，但从整体宏观上进行整体分析， 能够为学生提供新的视角和思路，就能出奇制胜，节省大量繁琐的计算过程，获得一条问题解答的捷径，优化初中数学问题的解答过程.

数学思想是一条穿梭于数学知识的线，它统领着整个数学和数学教育的思想， 它指导着研究数学和学习数学的人，更指导着数学核心素养.也就是说数学核心素养是数学基本思想在学习某一个或几个领域内容中的具体表现，而数学思想方法则是体现如何从操作层面上实现数学核心素养.在我们的教学中，我们应重视渗透数学思想，强化数学思想，为养成数学核心素养奠基，为学生终身学习数学的能力奠基.