轮盘-轴组件结合面螺栓等效刚度及其对动力学性能影响的研究*

（大连理工大学机械工程学院）

0 引言

旋转机械如压缩机等的转子系统，大量采用轮盘-轴组件形式的转子结构，且一般采用螺栓紧固连接。轮盘-轴组件的刚度特性直接影响转子系统刚度以及整机振动行为。受紧固螺栓和结合面几何误差以及紧固工艺的影响，轮盘-轴组件的结合面的螺栓连接存在复杂的受力和变形，在工况载荷的作用下，结合面会不断吸能和放能，表现出弹性和阻尼特性。

为了准确和方便的研究分析轮盘-轴组件结合面螺栓连接特性对转子系统的静动态特性影响，本文以某型旋转机械的一组轮盘-轴组件为对象，研究建立一种准确有效的方法处理轴盘组合类零部件结合面处的螺栓连接，对结合面螺栓连接特性对整体的动态特性影响进行量化研究分析。

结合面螺栓连接研究属于结合面动力学特性研究范畴，Andrew等[1]通过实验得出了结合面法向刚度和切向刚度的经验计算公式；吉村允孝[2]证明结合面接触面积不同但接触面平均压力相同，结合面每单位面积的动态数据均可应用于接触表面特性相同，而形状和接触面积不相同的结合面；王雯等[3]建立了机械结合面法向动态接触刚度理论模型，通过试验证明法向动态接触刚度和静态接触刚度与接触面压之间的关系；蔡力钢等[4]根据螺栓连接刚度、被联结件刚度、结合部刚度三者间函数关系计算出螺栓连接法向静态接触刚度非线性特性曲线。姚鹏等[5]采用弹簧-阻尼模型对结合面的螺栓连接进行等效处理，根据实验获取的结合面参数修正并建立刚度模型，以此研究特定对象的力学特性和模态参数。董冠华等[6]提取螺栓连接组合结构的模态分析数据搭建了MATLAB-ANSYS集成平台对螺栓结合部刚度进行辨识，结果表明栓接结构在较大预紧力作用下，螺栓结合部非线性动力学特性得到了抑制，满足线性条件假设。综上研究，大部分学者的研究对象中涉及到的螺栓连接大多属于有垫圈螺栓连接，对于无垫圈螺栓连接研究较少。另外，由于轮盘-轴组件具有结构复杂、结合面螺栓数量多，装配要求高的特点，目前较少有研究人员对此类部件的结合面特性进行研究。

本文针对某轮盘-轴组件的具体结构和无垫圈螺栓连接的特点，采用弹簧阻尼单元对结合面处的螺栓连接进行等效处理，并选用吉村允孝法计算结合面螺栓连接等效刚度。通过ANSYS workbench仿真分析轮盘-轴组件的螺栓连接等效刚度模型的动态特性，并通过模态实验对该等效刚度模型的动态特性进行验证。结果显示，该等效刚度模型能较为准确地模拟真实试件的动态特性。最后，基于该等效刚度模型，研究分析了螺栓结合面等效刚度值和离散度对轮盘-轴组件的模态频率影响规律。

1 螺栓连接等效刚度理论模型

某轮盘-轴组件由长轴和锥盘组成，结合面由环形均布的36组D型螺栓连接，如图1所示。由于结合面的存在，轮盘-轴组件在受工作载荷时，结合面不断吸能和放能，表现出弹性和阻尼的特性。这种特性受结合面的几何形状、几何形貌以及结合面之间的介质等因素的影响，这些非确定性因素造成了结合面受载荷时的非线性性质。为了更加准确和方便的仿真计算结合面螺栓连接特性对轮盘-轴组件动态特性的影响，本文采用弹簧阻尼单元等效处理结合面上各螺栓连接。每一组螺栓都由一个法向单元和两个切向单元构成。18组螺栓连接等效成弹簧阻尼单元如图2所示。

图1 某轮盘-轴组件结构示意图Fig.1 Structure of a disc-shaft assembly

图2 结合面等效模型Fig.2 Equivalent Model of Joint Surface

在动态特性分析中，真实结构的阻尼系数值要比临界阻尼小得多，通常为临界阻尼值的2%～10%，阻尼频率接近无阻尼固有频率，而阻尼的大小只会影响频响函数幅值的衰减速度和响应的峰值，因此可认为阻尼与固有频率无关[7，8]。为了计算方便，在有限元仿真模型中不考虑螺栓连接阻尼，仅考虑螺栓连接刚度。根据吉村允孝法可假设平面内单位面积上受到的压力为Pi，则

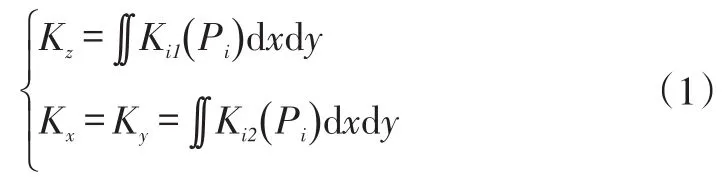
式中，i=1，2，3…n；Kz为结合面法向等效刚度，Kx,Ky为结合面切向等效刚度。Ki1(Pi)，Ki2(Pi)分别为第i个单位面积的法向和切向单位面积的等效刚度。结合面各向刚度与接触压强的关系可用式（2）表述：

式中，α,β是与结合面有关的常数。

将式（2）代入式（1）中即可得到各向等效刚度与接触压强的关系式（3）。

因此，只需要提取结合面面压数据即可计算出结合面各向等效刚度的数值。

2 仿真分析

2.1 仿真模型

轮盘-轴组件有限元仿真模型如图3。为了方便计算和实验，有限元仿真模型模拟结合面18组螺栓均布紧固情况，结合面的18组螺栓连接均采用弹簧单元等效，每组弹簧单元包括一个法向弹簧与两个切向弹簧。参照公式（3），每一组弹簧单元的各向刚度数值根据结合面面压数值计算得出。

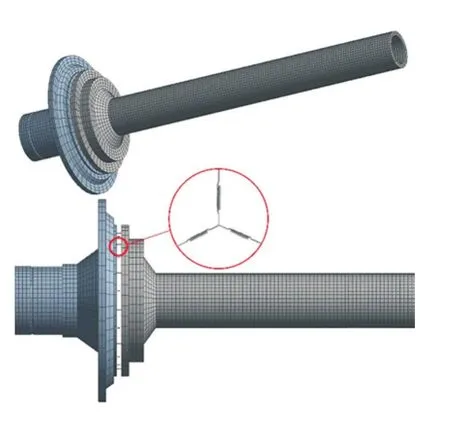
图3 有限元模型Fig.3 Finite element model

2.2 结合面面压提取

结合面面压提取试验中使用感压纸法提取面压。参考有限元仿真和实验测试结果，选择测试范围为10～50MPa的双片型中压（MW）感压试纸进行实验操作。双片型中压（MW）型感压纸的压力曲线图见图4。其中，图4a为检测瞬时压力曲线图，达到目标压力和保持压力时间均为5秒，图4b为检测连续压力曲线图，达到目标压力和保持压力时间均为2分钟。A,B,C,D曲线根据环境温度和湿度值选取。

图4 压力曲线图（中压）Fig.4 Pressure curve(MW)

感压纸安装位置如图5所示，考虑螺栓群位置分布和盘轴的拆卸难度，感压纸经过裁剪和打孔处理放入在结合面。结合面共紧固18组螺栓。紧固顺序采用图6所示的对角顺序拧紧，并一次施加70Nm扭矩。

感压纸提取面压后如图7a所示，经数字化处理后按1:1比例转换为数值矩阵，如图7b所示。感压纸每一个像素点为对应一个面压数值，相邻像素点之间的距离为实际尺寸的0.125mm,ΔS=1/64mm。

图5 感压纸安装示意图Fig.5 pressure test paper installation diagram

图6 螺栓紧固顺序Fig.6 Bolt fastening sequence

图7 感压纸提取面压Fig.7 Digitalization of pressure test paper Extraction Surface Pressure

2.3 结合面等效刚度计算

考虑到结合面单个像素点面积刚度计算，则公式1可变换为：

式中,Ki,Pi分别为结合面上第i像素点的刚度值与正压力；ΔS为单个像素点所占面积。从而结合面刚度可表示为：

式中，ΔS=1/64mm2。参考Ra=1.6的钢与刚接触结合面，结合面无油状态下的刚度计算[9]，取α1=779 644,β1=0.53，α2=779 644，β2=0.53。将感压纸提取的结合面各螺栓结合处的面压数值矩阵代入公式5中，得到结合面各螺栓连接刚度如表1和表2所示。

将表1和表2中计算出的结合面螺栓群各向等效刚度代入图2等效模型中。

3 螺栓刚度对动力学性能的影响

参考相关研究的模态试验自由边界模拟方法[10-11]，本模态测试实验中，选取16cm厚海绵支撑试件模拟被测试件的自由边界。实验中被测试件划分成128个测点，模态实验主要采用锤击法测量被测试件的固有频率和振型。测量系统包括：PCB公司力锤（中锤）和三向加速度传感器、NI公司9234型号采集卡和9188XT型号采集箱、24V稳压电源、装有东方所Coinv DASP MAS模态与动力分析软件的PC一台。测试系统如图8所示。

实验测得轮盘-轴组件的前六阶振型与仿真结果对比如图9所示。仿真和实验测得的模态前六阶固有频率对比结果如表3所示，为了方便对比，表3中参考了无结合面一体模型的有限元仿真模态前六阶固有频率数据。

表1 结合面各螺栓连接等效法向刚度Tab.1 Equivalent Normal Stiffness of Bolted Connections on Joint Surface

表2 结合面各螺栓连接等效切向刚度Tab.2 Equivalent Tangential Stiffness of Bolted Connections on Joint Surface

图8 模态测试系统Fig.8 Modal experimental system

表3 仿真与实验前六阶模态频率对比Tab.3 Comparison of the first six order modal frequencies between simulation and experiment

图9 轮盘-轴组件前六阶模态振型对比（上：仿真；下：实验）Fig.9 Comparison of the first six modal shapes(above:simulation;below:experiment)

4 螺栓刚度对模态频率的影响

相关研究表明结合面刚度对模型模态影响明显[11-13]，本文通过设置结合面等效弹簧刚度的数值和分散性研究分析结合面螺栓连接刚度大小及分布状态对轴盘模态频率的影响。

4.1 螺栓连接刚度值与模态频率的关系

为了简化计算量，仿真分析中将轮盘-轴组件模型中等效螺栓的弹簧阻尼单元数量减少至6组。法向刚度等值分成20组，将求得的各阶振型所对应频率绘制成图，如图10所示。

图10 模态频率与螺栓连接刚度的关系Fig.10 Relationship between Modal Frequency and Bolted Joint Stiffness

从图10中可以看出，随着结合面等效的各螺栓连接刚度数值同时增大，各阶振型所对应频率数值也随之增大。其中，前三阶振型对应的频率影响较为明显，一阶、二阶、三阶频率数值分别提高了51.2%，56.4%和23.4%，而第四阶、五阶和六阶振型对应的频率数值受影响较小，分别提高了4.0%，4.4%和1.2%。在螺栓的等效连接刚度数值增大到一定量时，各阶频率数值逐渐趋于稳定。

4.2 模态频率与螺栓连接刚度分散性的关系

实际工程中常采用扭矩法加载螺栓预紧力，扭矩与预紧力转换的不确定性以及螺栓组之间的弹性相互作用关系，导致螺栓组最终残余预紧力的离散度能高达±30%左右，从而影响螺栓连接刚度的大小及分散性。标准差是影响离散度的主要参数，本文利用Matlab生成一组均值相同，标准差不同的随机数列，将该数列的数值分别代入轮盘-轴组件模型中的等效螺栓连接刚度，然后进行模态分析计算得到各阶振型数据。模型的螺栓组连接刚度平均值设置为5×108N/m，共生成了9组梯度标准差的数据，模态频率曲线如图11所示。

图11 模态频率与螺栓连接刚度分散性的关系Fig.11 Relationship between modal frequency and stiffness dispersion of bolted connections

从图11中可以看出，当各螺栓连接等效刚度均值相同时，随着螺栓连接刚度标准差增大，轮盘-轴组件各阶振型对应的频率虽然呈下降趋势，但是影响不大。前六阶振型对应的频率数值分别下降了1.6%，8.7%，0.2%，8.3%，6.0%，0.1%。

5 结论

1）轮盘-轴组件结合面螺栓等效模型有限元模态仿真的各阶振型对应的频率数值与实验测得的各阶振型对应的频率数值误差均在在10%以内，其中轮盘-轴组件整体模态误差在2%以内，采用弹簧单元等效处理螺栓连接的模型能较为准确的计算结合面特性对轮盘-轴组件动态特性的影响。

2）轮盘-轴组件螺栓连接中，各螺栓等效刚度均值大小和轮盘-轴组件模型的模态特性成正相关关系，即等效刚度均值增大，轮盘-轴组件模态各阶振型对应的频率也随着增大。各螺栓等效刚度的离散性与轮盘-轴组件模型的模态特性成负相关关系，即等效刚度均值不变，标准差增大，各阶振型对应的频率随着减小。