婴幼儿语音信息处理与识别研究模型

左正东， 万光彩， 杜佳轩

安徽财经大学金融学院，安徽 蚌埠 233000

幼儿专家的研究成果表明，婴儿的情绪表达不仅是与外界交流的主要方式，而且是反映其生理和心理需求、身心健康状态及其智力发育水平的重要信息来源[1].20世纪60年代，国外有研究小组能完成对病理性的啼哭声和非病理性的啼哭声进行模式区别，但是目前对婴儿语音信息的研究，还主要关注的是简单的疼痛或者啼哭上，并未结合婴儿的具体情感需求，可能更多还是对啼哭声的研究[2].目前相关的文献，并没有关于婴儿的情绪管理标准的分类方法，在情感语音识别的实验中，如何将婴儿的情感进行分类，及相应的语音信息中，某种特征参数的含义在目前的研究中并未给出一个清楚的划分.本文将对婴儿的情感信息进行分类，同时对可用于婴儿语音识别的技术进行了研究，最后对采集到的婴儿语音信息样本进行了一个简单的语音信息识别实验.

1 数据来源及假设

数据来源于搜集到的婴幼儿愉悦时发出的声音，一男一女分别唱同一首歌的音频，不同程度喜悦状态下的婴幼儿发出的声音.为了便于解决问题，提出了以下几条假设：(1)短时傅立叶变换已经完全去除样本的杂音，不存在可以影响样本特质的外界因素存在；(2)选取的男女样本差异是准确的；(3)忽略愉悦语音库中部分愉快情绪样本不足所产生的偏差.

2 基于梅尔频率倒谱系数和贝叶斯判别对语音信息的判别归类

2.1 研究思路

对于一男一女唱同一首歌的音频，首先基于性别差异角度对语音信号时域进行特征分析，通过绘制语谱图、能量图、相关函数图等，观察男女声的差异，可以发现语音信号前100帧的性别差异特征较为明显，以此样本代替整体，再利用MFCC分别得到男性和女性语音的48 110*24 MFCC特征矩阵.通过贝叶斯判别法，将语音进行性别判别归类，再利用该模型对婴儿的声音进行鉴别.

2.2 研究方法

2.2.1 梅尔倒谱系数

在语音识别(Speech Recognition)和话者识别(Speaker Recognition)方面，最常用到的语音特征就是梅尔倒谱系数(Mel-scale Frequency Cepstral Coefficients，简称MFCC).梅尔倒谱系数是在Mel标度频率域提取出来的倒谱参数，具有较强的识别性能和抗噪声性能，但它的计算要求是计算精度高[3].Mel标度描述了人耳频率的非线性特性，它与频率的关系可用下式近似表示

(1)

其中，f为频率，单位为Hz.图1展示了Mel频率与线性频率的关系.

图1 Mel频率与线性频率的关系图
Fig.1 Diagram of Mel frequency and linear frequency

语音特征参数MFCC提取的基本流程(图2)如下.

图2 语音特征参数MFCC提取过程
Fig.2 Speech feature parameters MFCC extraction process

2.2.2 贝叶斯判别

两个总体协方差矩阵相等的情形

设总体G1、G2的协方差矩阵相等且为Σ，概率密度函数为

(2)

总体G1、G2的先验概率为p1=P(G1),p2=P(G2)(p1+p2=1),则基于两正态总体误判损失相等的贝叶斯判别(Bayesian Discriminant)准则为

(3)

(4)

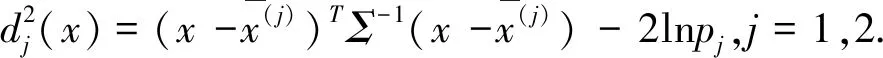
平均误判率

贝叶斯判别的有效性可以通过平均误判率来确定.这里仅对两个正态总体G1、G2，且协方差矩阵相等的情况下研究平均误差率的计算[4].

设总体Gi～Np(μj,Σ)(i=1,2),总体G1、G2的先验概率p1=P(G1),p2=P(G2)(p1+p2=1),两个总体G1、G2的马氏平方距离记为

δ=(μ1-μ2)TΣ-1(μ1-μ2)

(5)

则基于误判损失相等时的平均误判率为

(6)

其中,d=lnp1～lnp2,Φ(·)为标准正态分布函数.图3显示了婴儿愉悦时的语音特点，其中我们可以看出其波动的时长大约2 s，其频率为40 000 Hz.

图3 时间频率图Fig.3 Time frequency graph图4 MFCC与峰值、维数与幅值的关系Fig.4 The relationship between MFCC and peak, dimension and amplitude

由图4可知，梅尔频率倒谱系数的幅值总体在5到25之间，图5是维数与幅值的关系，我们发现随着维数的增加，幅值从3 500，在逐渐减少.

通过比较，我们发现其语音的幅度与维的关系为随着维数增加，幅度逐渐趋于平稳，变小，而幅图6展示是桢数在10000的计量单位下的情况，我们发现桢数变多时曲线变得越来越细密.

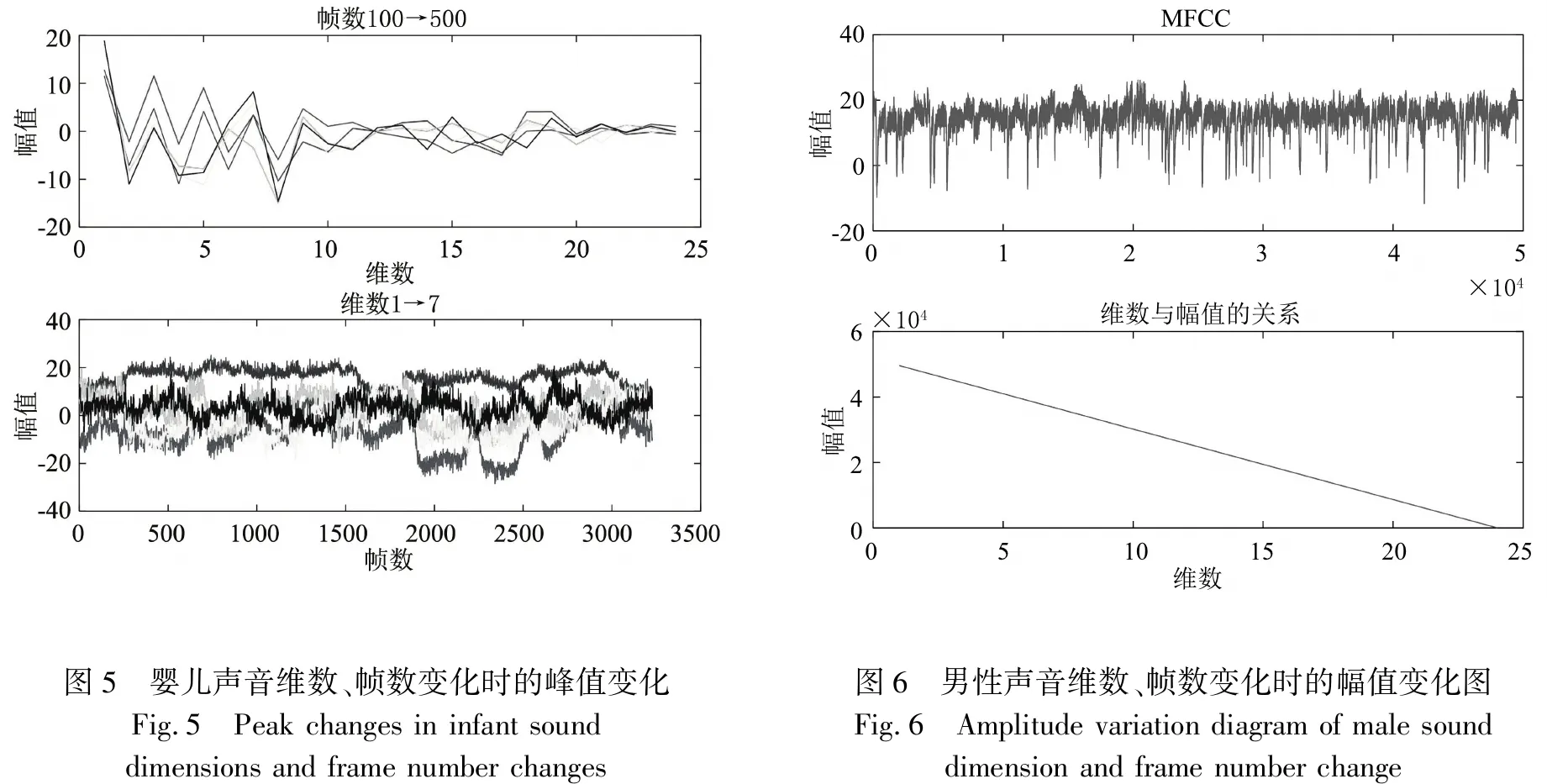
图5 婴儿声音维数、帧数变化时的峰值变化Fig.5 Peak changes in infant sound dimensions and frame number changes图6 男性声音维数、帧数变化时的幅值变化图Fig.6 Amplitude variation diagram of male sound dimension and frame number change

由图6可以发现，男性和女性在声音频率、振幅方面一定有很大区别，其中男音频振幅较大，对于女性，我们发现其语音的幅度较为平稳，密集，女性的梅尔频率倒谱系数的幅值总体较之男生较为细密整齐，大多集中在18，图7是维数与幅值的关系，我们发现随着维数的增加，幅值在逐渐减少，从40000开始.其幅值整体高于男性.

2.3 模型的建立与分析——基于性别差异角度语言信号时域特征分析

(1)语音信号的声谱图和短时谱

用wavread 函数加载一段语音信号，对其进行加窗处理，由于矩形窗的主瓣宽度小(4*pi/N)，具有较高的频率分辨率，旁瓣峰值大(-13.3 dB)，会导致泄漏现象；汉明窗的主瓣宽8*pi/N，旁瓣峰值低(-42.7dB)，可以有效地克服泄漏现象，具有更平滑的低通特性.因此在语音频谱分析时常使用汉明窗.实验结果如图8所示.可以发现，男性发声能量在0上下震动.时间越长波动越大，幅度值呈周期性变化.

(2)语音信号的语谱图(图9)

男性愉悦时发音频率不同时间下，平均起来超过15 000 Hz，约处在17 000 Hz左右.

(3)短时能量(图10)

图7 男性MFCC相关图Fig.7 Correlation diagram of male MFCC图8 男性短时谱图Fig.8 Short time spectra for men

根据N的不同，波形不同，窗过大(N很大)，等效于很窄的低通滤波器，不能反映幅度En的变化；窗过小(N很小)，短时能量随时间急剧变化，不能得到平滑的能量函数.由此N选为100～200比较合适.在此情况下，发现峰值是在相应的变大，峰值范围在6到10之间.

(4)短时平均过零率(图11)

过零率可以反映信号的频谱特性.当离散时间信号相邻两个样点的正负号相异时，我们称之为“过零”，即此时信号的时间波形穿过了零电平的横轴.统计单位时间内样点值改变符号的次数具可以得到平均过零率.

分析结果：男性的短时平均过零率在随时间不断变大，2.5到3.5(106)达到最值.

(5)短时自相关函数(图12)

自相关函数用于衡量信号自身时间波形的相似性.清音和浊音的发声机理不同，因而在波形上也存在着较大的差异.浊音的时间波形呈现出一定的周期性，波形之间相似性较好；清音的时间波形呈现出随机噪声的特性，样点间的相似性较差.因此，我们用短时自相关函数来测定语音的相似特性.

分析结果：男性的短时间自相关函数为曲线形.先下降后上升.

(6)短时平均幅度(图13)

由于短时能量函数的En对信号电平值过于敏感，需要计算信号样值的平方和，在定点实现时很容易产生溢出，因此可定义一个平均幅度函数Mn来衡量语音幅度的变化.

图9 男性语谱图Fig.9 Male language spectrum

图10 男性短时能量图
Fig.10 Short time energy graph for men

图11 男性短时平均过零率图Fig.11 Men's short time average over 0 rate chart图12 男性短时自相关函数图Fig.12 Male Short-time auto-correlation function diagram

图13 男性短时平均幅度图Fig.13 Figure of short-term average ranges for men图14 女性维数、帧数与幅值关系图Fig.14 Diagram of female dimension, frame number and amplitude

分析结果：男性的短时间平均幅度先增大后减小，峰值在2.5到3(106)之间.

由图14可以发现，女性梅尔频率倒谱系数的幅值在20左右低于男性，图15是维数与幅值的关系，我们发现随着维数的增加，幅值从50 000在逐渐减少，高于男性.

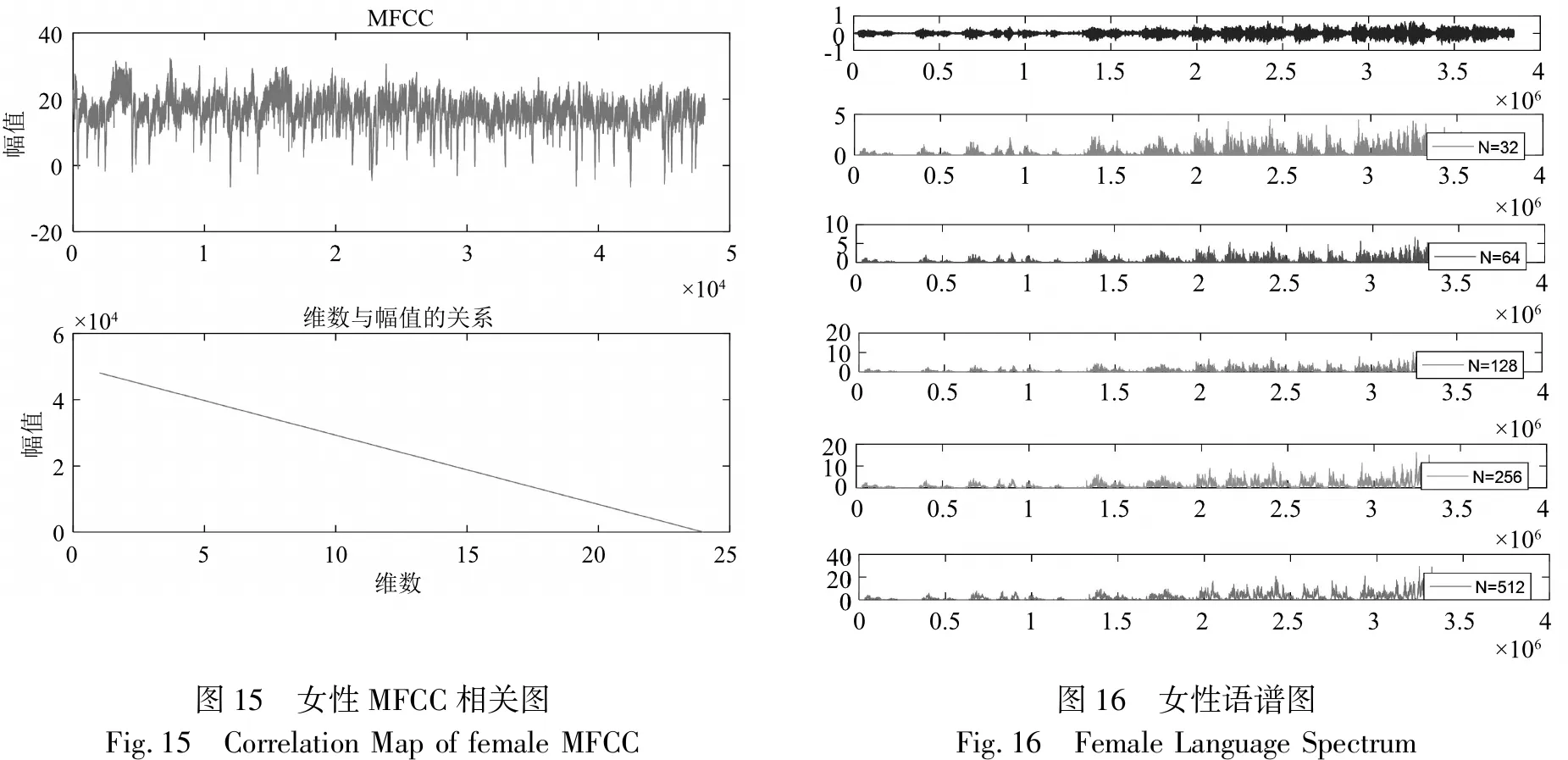
图15 女性MFCC相关图Fig.15 Correlation Map of female MFCC图16 女性语谱图Fig.16 Female Language Spectrum

女性愉悦时发音频率与男生较为相似，平均起来超过15 000 Hz，约处在17 000 Hz左右.由此可见女性的短间能量在N在100到200之间时总体高于男性，最高接近20.

女性的短时平均过零率在随时间不断变大，与男性一样在2.5到3.5(106)达到最值.

女性的短时间自相关函数为曲线形.先下降后上升.其最低值在80左右，后又上升再下降.

由此可见，女性的短时间平均幅度同样先增大后减小，峰值在0.2*106.总体低于男性.

利用MFCC分别得到男性语音的48 110*24 和女性语音的49 220*24的MFCC特征矩阵.基于MFCC参数进行贝叶斯判别，贝叶斯判别要求总体呈正态分布，利用Matlab绘制QQ图，结果如下，可以看出其呈显著的正态分布，因此可以判别.

图17 女性短时能量图Fig.17 Short time energy graph for women图18 女性短时平均过零率图Fig.18 Female short time average over 0 rate chart

图19 女性短时自相关函数Fig.19 Female short-term self-correlation function图20 女性语音短时平均幅度图Fig.20 Graph of short-term mean ranges for female voice

表1 男女语音特征的均值向量比较Tab.1 Comparison of mean vectors for phonetic features of men and women

但是将男性语音与女性语音所有帧数的特征值均引入的话，会导致数据量过大，运算困难，又通过前面所做的语谱图分析可知，男女性在唱“谎言”这首歌时，其性别差异主要来自前部，因此选取男女音频的前100帧，作为分类的学习样本，将附件中的前100帧作为判别样本.

分别计算女性语音样本和男性语音样本的均值向量、协方差、样本数以及二者混合的样本数.

计算混合样本方差24*24矩阵，然后得到女性语音样本与男性语音样本的协方差Qfemale=5.415 628 859 825 042e+02，Qmale=4.441 004 676 950 699e+02，协方差不相等，因此进行下一步操作，利用判别函数得出前100帧均有男性特征.

图21 原始数据检验图
Fig.21 Raw Data Inspection diagram

误差分析，利用Matlab计算回代误判率为0，因此婴儿性别为男.

3 结语

本文针对婴儿语音的识别及处理问题，通过Mel尺度倒谱参数(MFCC)等信号分析的参数，基于性别差异角度对语音信号时域进行特征分析，绘制语谱图、能量图、相关函数图等，观察男女声的差异，通过贝叶斯判别法，将语音进行性别判别归类，再利用该模型对婴儿的声音进行鉴别.模型中为使计算简便，使所得结果更理想化，忽略了一些次要影响因素.模型使用的音频样本不够丰富，也使模型准确性有所降低.巧妙运用多种数学软件(如MATLAB、Excel),取长补短，使计算结果更加准确、明晰.本文建立的模型与实际紧密联系，充分考虑乐理等科学知识，从而使模型更加通用、易懂.