合作对策的边际预核子
2019-06-17张莉
张莉
长治学院数学系, 山西 长治 046011
合作对策理论主要研究如何分配合作所产生的收益, 在日常生活中有广泛的应用. 例如股东的权利分配, 企业间合作的收益分配, 银行破产债务分配等等. 在合作对策中, 不同的分配原则会得到不同的分配结果.1953年Shapley基于边际贡献提出了Shapley值[1,2]. 1965年Davis和Maschler基于超量和最大剩余值提出了核[3].1969年Schmeidler基于超量提出了核子[4], 超量是用来衡量联盟抱怨(联盟不满意度)的, 核子就是基于联盟抱怨用字典序的方法在分配集中找到的最优解.自此,众多学者将核子进行了推广,得到了预核子[5]、广义核子[6]、Modified Nucleolus[7]、SM-核子[8]、SD-核子[9]等等, 这些都是基于联盟抱怨且都是用字典序的方法得到的解. 除用字典序的方法之外, Ruiz在1996年提出了最小平方预核子[10],在1998年提出了最小平方值[11],他用的是最优化的方法选择最优分配使得各个联盟的不满意度变化最小化.之后在2000年Molina和Tejada给出了最小平方核子与广义核子的关系[12].相较于基于联盟不满意度的解的研究的多样化,从单个参与者自身的角度入手, 基于单个参与者的不满意度的解的研究相对很少, 1994年Sakawa和Nishizaki首次从单个参与者的角度考虑对分配的不满意度, 通过定义参与者超量得到了字典序解[13].
本文主要从单个参与者对于分配的不满意度入手, 提出了新的衡量每个参与者不满意度的标准, 基于这一标准用字典序的方法在预分配集中得到最优解, 将该解称为边际预核子, 并对其进行了公理化研究以说明该解的公平合理性.
1 基本概念

GN表示定义在集合N上的所有具有n个参与者的合作对策的集合.2N表示N的所有子集,N的子集S(S⊂N)称为一个联盟, 实数v(S)表示联盟S中的成员通过合作所能获得的价值. 在不引起混淆的前提下, 为了方便使用, 我们用v代表对策(N,v), 用v(i)代替v({i}).

定义3对于任意n人对策v∈GN,支付向量x是有效的[1],若大联盟的收益全部分给所有参与者,即
x(N)=v(N)
支付向量x是个体理性的, 若对任意的参与者i∈N在支付向量x下获得的收益不少于它单干的价值,即
xi≥v(i)
支付向量x是联盟理性的, 若对任意的联盟S⊂N在支付向量x下获得的收益不少于联盟S的价值, 即
x(S)≥v(S)
所有满足有效性的支付向量的集合称为预分配集, 记作I*(v), 即
I*(v)={x∈Rn|x(N)=v(N)}
所有满足有效性和个体理性的支付向量的集合称为分配集, 记作I(v), 即
I(v)={x∈Rn|x(N)=v(N)且xi≥v(i),对任意的i∈N}
对于任意n人对策v∈GN和支付向量x∈Rn,联盟S的超量为
e(S,x)=v(S)-x(S)
由超量的定义可知,联盟S的超量e(S,x)可以看成是联盟S中的成员对于支付向量x的不满意度或抱怨.e(S,x)越大, 联盟S中的成员越感到受到不公平对待, 不满意度也越大.
核子[4]是合作对策中一个非常重要的单值解, 它是基于超量的, 也可以说是基于联盟抱怨的.
定义4令θ(x)是一个2n维的向量, 它的分量为e(S,x)(S⊂N), 并按照非递增的顺序排列. 即
θi(x)≥θj(x) 1≤i≤j≤2n
则θ(x)可看作是抱怨向量.
我们用字典序的方法对抱怨向量θ(x),x∈Rn进行排序, 字典序记为“≤L”.对于任意的x,y∈Rn有
θ(x) θ(x)≤Lθ(y) 若θ(x) 核子是在分配集中使得抱怨向量θ(x)按字典序最小的解.即 η(v)={x∈I(v)|θ(x)≤Lθ(y)},对任意的y∈I(v)} 本节将从参与者个体抱怨的角度得到一个新的合作对策解——边际预核子,并给出边际预核子所具有的一些好的性质, 最后给出边际预核子的公理化证明. 核子是从联盟抱怨的角度, 考虑每一个联盟对于某个分配的不满意度, 而作为合作中的每一个参与者也应该都有各自对于某一分配的不满意度. 在这一小节中基于参与者个体的不满意度, 首先给出了一种新的参与者不满意度衡量方法. 定义5对于任意对策v∈GN和任意支付向量x∈Rn,参与者i∈N的边际超量为 ei(x)=e(N,x)-e(Ni,x) 定义7对任意对策v∈GN, 在预分配集I*(v)中满足 的预分配x*是边际预核子. 因此, 边际预核子是在预分配集中选择使得边际抱怨向量按字典序排列最小的解. 这个解通过最小化边际抱怨向量来尽量达到公平合理. 为了能给出边际预核子的解析表达式, 我们首先给出下列推论. 推论1对任意对策v∈GN,边际预核子x*满足 据勘查,昌乐境内蓝宝石富矿区450平方公里,储量数十亿克拉,占全国蓝宝石总储量的90%以上,是继泰国、澳大利亚、斯里兰卡蓝宝石矿之后世界上发现的第四大蓝宝石矿床。昌乐蓝宝石化学成分和矿物成分与缅甸、泰国、柬埔寨、斯里兰卡等国家生产的蓝宝石并无大的不同,“其化学成分主要是三氧化二铝,就是金属铝的氧化物,因为含有微量元素钛和铁而呈现蓝色,并且具有颗粒大、颜色纯、质量好、双色性、易开采、奇异宝石多等特点。尤其是昌乐蓝宝石独有的双色性,即表面呈现蓝色,侧面则是神奇的绿色,颇受国内外珠宝界青睐,昌乐也因此被誉为“蓝宝石之都”。 对任意的i,j∈N恒成立. 证明 我们用反证法来证明上述结论. 假设存在l,h∈N,使得 我们不妨假设 也就是说 1≤h 令 那么我们可以构造新的解x**∈Rn, 使得 则 但是 因此, 证毕. 定理1对任意对策v∈GN,边际预核子可以表示为 证明 首先, 在对策v∈GN中, 对任意预分配x∈I*(v) 是常数. 又由推论1,边际预核子x*满足 即 ei(x*)=ej(x*) 对任意的i,j∈N恒成立.所以, 证毕. 定义8一个支付向量x∈Rn满足边际超量相等性, 若对任意的对策v∈GN和任意的i,j∈N且i≠j,有 ei(x)=ej(x) 定理2边际预核子是唯一满足有效性和边际超量相等性的解. 证明 由边际预核子的定义及推论1可知, 边际预核子满足有效性和边际超量相等性. 为了证明边际预核子是唯一满足有效性和边际超量相等性的解, 我们假设存在两个支付向量y1,y2∈Rn同时满足以上两个性质, 则必有y1=y2. 在对策中v∈GN,对任意预分配x∈I*(v) 是定值, 我们把该定值记为C.由于向量y1,y2都满足个体超量相等性, 所以对任意参与者i∈N,有 即 ei(y1)=ei(y2) 对任意参与者i∈N都成立.由此可得y1=y2. 下面我们来证明上述用来公理化边际预核子的两个性质是逻辑独立的. * 考虑解 该解只满足边际超量相等性不满足有效性.证毕. 本文主要从参与者个体的角度, 通过衡量每个参与者对于某个分配的不满意度, 在预分配集中得到了一个新的解,即边际预核子.为了进一步说明它的公平合理性, 我们进行了公理化研究.边际预核子对于在实际合作中每个参与者如何分配合作所产生的收益具有一定的意义,但边际预核子也损失了v(S),|S|≤n-2所包含的信息.如何将对策的所有信息包含在内是我们未来进一步研究的方向.此外除了对新的解进行公理化之外,我们还可以从非合作的角度进行非合作机制设计[14],例如投标机制设计[15],以说明它的公平合理性.2 主要结论
2.1 边际预核子
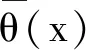
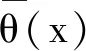
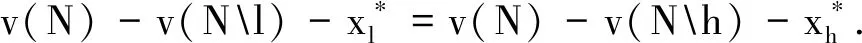
2.2 边际预核子的公理化

3 结语
