二维异质结MoS2/WSe2能带排列的第一性原理研究

葛梅， 杨国晖， 张均锋

山西师范大学物理与信息工程学院，山西 临汾 041000

0 引言

自从石墨烯被成功制备以来，只有单原子层或几层原子厚度的二维纳米材料(简称为二维材料)吸引了研究者极大的研究兴趣[1].二维材料家族成员众多且性质各异，从金属性的硼烯(Borophene)[2]或者MXene[3]等，到半导体性的黑磷(Black Phosphorus)[4]，MoS2[5]，WSe2[6]等等，再到绝缘体性的六角氮化硼(h-BN)[7].近年来人们还得到了二维磁性材料比如Cr2Ge2Te6[8]和CrI3[9].将这些二维材料中的两个或多个组合成二维异质结形式，可以应用于肖特基二极管、场效应管、光电器件以及集成电路等等，成为最近几年研究的热点.

目前，根据组分材料间结合方式的不同，大部分理论研究者都将二维异质结分为二维层内异质结和二维层间异质结两种不同的形式.将两种或几种不同的二维材料依次铺在一起，就得到二维层间异质结.因此，二维层间异质结形成比较容易，其物理性质控制也相对比较简单，因此得到了人们广泛的研究.而在二维层内异质结中，体系能保持其原有的单层或者少层的特点，两种二维材料组分通过线界面结合，这也对组分二维材料之间的晶格匹配度要求较高.二维层内异质结由于其对晶格适配度的高要求，制备上具有一定的难度，但是能保持原有层数，因此在薄膜电路等方向具有非常诱人的应用前景，近年来得到了实验和理论研究者的重点关注.

我们发现，在部分层内异质结的实验制备中，如果两种组分二维材料的晶格失配度比较大.原本希望通过线界面连接的二维层内异质结，则有可能形成双层区域的界面[10].同时，对于实验室制备的二维层间异质结，在器件应用中，由于电极等因素也不再是完美的层间异质结结构[11].近来，研究者开始关注此类的结构，从理论角度往往是通过构建单层-双层的结构模型，这对研究部分同种材料不同层形成的异质结是有效的.但是对于大部分的异质结来说，对于从理论建模的角度，周期性边界条件导致很多异质结很难在一个模型中得到理论结果，必须将异质结分成两部分来进行研究.

能带排列是指，在半导体异质结中，两种组分材料的价带顶或者导带底差.作为基本参数之一，能带排列决定了基于异质结器件的性能，比如二极管等.因此，自从20世纪六七十年代开始，如何准确给出半导体异质结的能带排列就成了人们关注的热点问题之一.当界面作用较强，可以聚集一定的电子从而钉扎住费米能级；而当界面作用较弱的时候，两种材料的能级位置几乎不受界面和另一种材料的影响，称为安德森极限(在金属半导体异质结中则称为肖特基莫特极限，两个概念的物理图像是相同的).而在二维异质结中，最近的理论和实验报道表明，由于层内异质结真空的弱屏蔽作用以及层间异质结中两种材料间的弱相互作用，其能带排列都趋于安德森极限.这和传统的三维异质结具有不同的物理图像，也使得二维器件具有三维情形所不具备的优势.

在本文中，从第一性原理计算的角度，我们介绍一种由MoS2和WSe2组成的新奇二维异质结里面的能带排列问题.我们分别计算了MoS2和WSe2的能带结构和电子态密度.使用周期性边界条件分别构建了两种结构，MoS2/MoS2-WSe2以及WSe2/WSe2-MoS2.两种结构中，能带位置随着双层区域的尺寸而变化.将两部分的结果结合起来，我们就可以得到整个系统的能带排列趋势.最后进行总结，给出二维复杂界面异质结一个例子的能带排列情况.

1 计算方法

在所有的计算中，我们都是用了基于密度泛函理论和缀加平面波[12]的第一性原理模拟软件vasp程序包[13]，用Perdew-Burke-Ernzerhof (PBE)[14]方法来描述电子的交换关联作用.通过测试计算，我们选取500 eV电子伏的截断能，选取了0.015每埃的K点密度，同时选取了5 nm的真空来屏蔽周期性镜像的作用.分别选取10-4eV和0.01 eV作为几何结构优化和电子循环的收敛判据.

2 主要结论

首先，考察二维材料MoS2和WSe2的体相结构和电子性质.图1(a)和图1(b)分别展示了MoS2和WSe2的单胞结构.我们将两种材料的晶格参数统一设置为MoS2的晶格(0.319 1 nm).需要指出的是，和图1(c)中展示的侧视图一样，二维材料MoS2和WSe2都是三层原子结构，而不是和石墨烯以及六角氮化硼类似的单原子层结构.在计算体相性质时，我们使用了方格子作为单胞，而不是常用的六角晶格.这样的选择，会导致对称性在某些方向上的丢失，进而影响能带结构(图2)，优点是，能够更方便的比较在异质结中的电子结构.

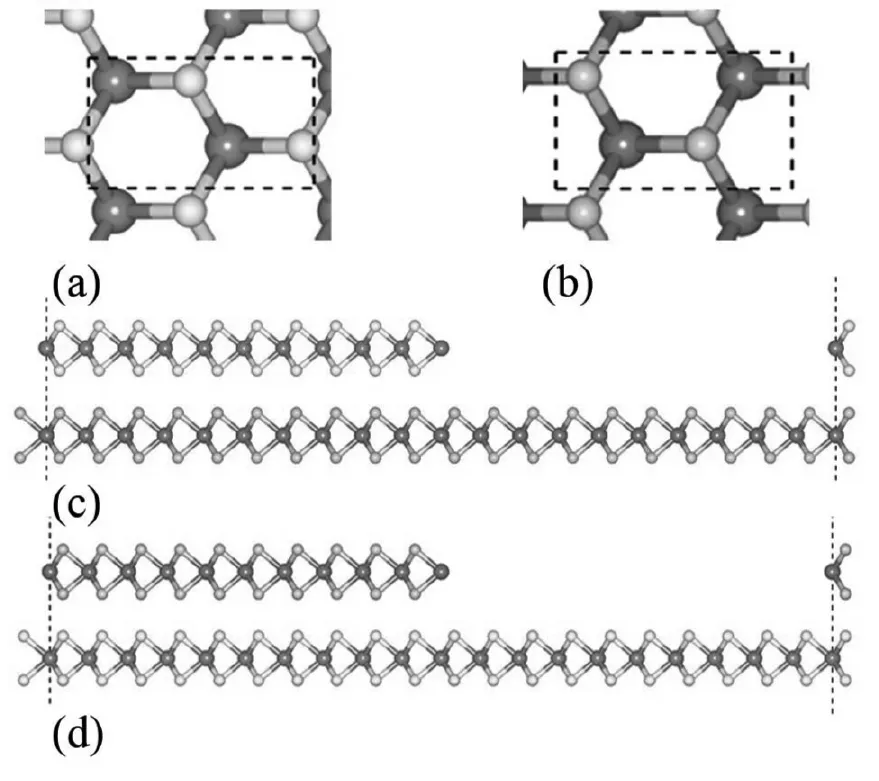
图1 (a)二维材料MoS2的俯视图;(b)二维材料WSe2的俯视图;(c)MoS2/WSe2-WSe2异质结的侧视图；(d)MoS2/WSe2-MoS2异质结的侧视图.图中虚线表示晶胞.

Fig.1 (a) Top view of 2D materials MoS2; (b) Top view of 2D materials WSe2; (c) Side view of 2D MoS2/WSe2-WSe2heterostructures; (c) Side view of 2D MoS2/WSe2-MoS2heterostructures. Dashed line here labeled the unit cell

图2展示了体相时MoS2和WSe2的能带图.首先，MoS2和WSe2的带隙分别为1.45 eV和1.60 eV，这和之前的理论计算符合比较好.其次，我们可以看到，WSe2的导带底和价带顶都位于X’和G点之间，为直接带隙半导体.而对于MoS2来说，导带底位于X’和G点之间，但是价带顶位于G点，因此为间接带隙半导体.我们的计算显示，二维WSe2中，真空能级(EV)为1.303 eV，费米能级(EF)为-3.702 eV，在图2a中，导带底和价带顶分别为-0.05 eV和1.4 eV.因此，依据真空能级，WSe2的导带底和价带顶真实位置位于：-3.605 eV，-5.055 eV.同样的，在MoS2中， EV= 1.313 eV， EF= -4.544 eV，而导带底和价带顶分别为-0.082 eV和1.519 eV，因此其导带底和价带顶真实位置位于：-4.338 eV，-5.939 eV.因此，在理想的安德森极限下，导带底和价带顶的能带偏移分别为0.733 eV和0.884 eV.

然后，我们将MoS2和WSe2组合成异质结的形式.真实的异质结，应该是具有MoS2-MoS2/WSe2-WSe2的形式.这里，“-”表示层内通过线界面连接，“/”则表示层间异质结，通过面界面相连.但是，在周期性边界条件的限制下，我们没办法在一个计算单胞中实施这样的计算.因此，我们设计了图1(c)和1(d)所示的结构，进行两步法计算.在模型中，双层部分具有相同的形式，都为AB堆叠的双层MoS2/WSe2结构.但是图1(c)和1(d)中的单层部分分别为MoS2和WSe2结构.这样，两种结构其实都是单层-双层的异质结结构.实际上，双层区域是整个系统中的界面部分，但这里是作为异质结的一半来处理的.这样，要得到整个系统，从MoS2到WSe2的能带偏移情况，需要中间双层区域当作中间体.先求出异质结MoS2-MoS2/WSe2的能带偏移，再求出异质结MoS2/WSe2-WSe2的能带偏移，最后扣除掉中间MoS2/WSe2部分，得到从单层MoS2到单层WSe2的能带偏移.显然，总体的能带偏移情况会依赖于双层区域宽度，这种宽度依赖效应部分原因是由于模型计算中的周期性边界条件.因此，本文的计算中，我们各使用了四种不同尺寸的原胞(L)：2.2 nm, 2.7 nm, 3.3 nm和3.9 nm.希望在能通过不同长度下的能带排列，过滤双层区域长度效应，从而找到真正的具有复杂界面异质结的能带排列规律.

图2 单层体相(a)WSe2和(b)MoS2的能带图
Fig.2 Band structures of bulked monolayer Se2(a) and MoS2(b)

图3 异质结MoS2-MoS2/WSe2(左)和异质结MoS2/WSe2-WSe2(右)的原子投影态密度示意图.其中从灰色到黑色表示原子贡献态密度从大到小过渡，白色线表示费米能级位置

Fig.3 The atomic projected density of states for MoS2-MoS2/WSe2(left) and MoS2/WSe2-WSe2(right) heterostructures. The black means zero contribution, and grey means 100 % contribution. The write line label the Fermi level

在图3中，针对原胞长度为2.7 nm的胞，我们画出了实空间原子投影的局域态密度图.针对X处的原子，计算出在X方向一个原胞内、Y方向所有原子的态密度.在此异质结内，需要去除边界效应，因此我们仅仅考虑X/L从0.2到0.8范围内局域态密度的变化.在图3中，左侧图对应MoS2-MoS2/WSe2异质结，而右侧图对应MoS2/WSe2-WSe2异质结.从黑色到灰色，表示该处原子对态密度贡献的从低到高转变.首先，我们可以看到，无论是对MoS2-MoS2/WSe2异质结还是MoS2/WSe2-WSe2异质结，在晶胞中心位置，带隙都明显降低.这是由于在双层和单层的交界处，部分原子是处于未饱和状态的.这些原子中的未成对电子，导致在局域部分的金属性.但是，我们应该清楚，在真实情况下，这些未成对的电子都会被氢等元素饱和，从而带隙升高，使得体系呈现半导体性质.其次，从图3的左右对比可以看出，双层区域虽然是相同的材料，理论上应该具有相同的带隙宽度，具有相同的带边位置.但是，由于一方面两种单胞内界面部分结构不同(一个是MoS2的边界，另一个则是WSe2的边界)，另一方面不同区域对应的真空能级也有差异，这导致两部分的能带结构费米能级位置不同，带隙宽度也有稍微不同.在理解这两个方面的前提下，我们可以从图中直接读取单层区域和双层区域的能带排列情况.

最后，我们将两个区域的能带偏移情况合并到一起，就可以得到整个系统的能带偏移情况.如图4所示，随着晶胞参数的不断增加，无论是导带还是价带的能带偏移值，都逐渐上升.之前的理论研究表明[15]，在面内异质结中，其能带偏移情况与晶胞长度和真空层厚度两个因素有关，只有当二者同时趋于无穷大时，能带偏移才能达到安德森极限或者肖特基莫特极限.从图4可以看出，在当前真空层不变的情况下，随着晶格长度的增加，无论是导带底还是价带顶的能带偏移都在逐步接近安德森极限：0.733 eV和0.884 eV.单层-双层边界的影响随着距离的增加而减小，在无限大原胞中，这种复杂界面的异质结能带排列也为安德森极限类型.

图4 异质结MoS2-MoS2/WSe2-WSe2中能带排列随晶胞宽度变化的趋势图.虚线和点线分别表示导带和价带的能带排列安德森极限值

Fig.4 The band offset in MoS2-MoS2/WSe2-WSe2heterostructures. Dashed line and dotted line corresponding to the Anderson limit in band offset of CB and VB.

3 结论与建议

我们采用第一性原理方法对一种具有复杂界面的异质结进行了能带排列的研究.使用两步模型，可以有效得到这种复杂界面的能带排列情况.通过局域电子态密度计算，我们发现，在组成异质结材料之后，随着双层区域尺寸的增加，其价带顶和导带底都会有连续的变化，能带排列最终将符合安德森极限.此结果对理解各种类型的二维异质结能带排列情况和低维器件的性能变化提供了理论支持.