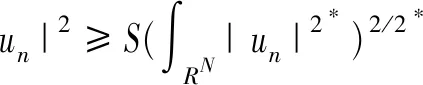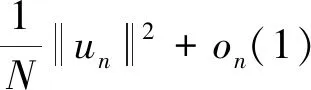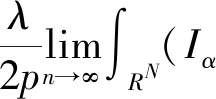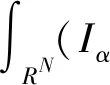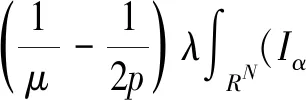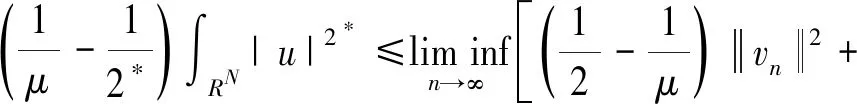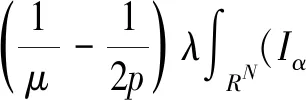带有临界项的Choquard方程的基态解
2019-06-14黄永艳
龙 雷,黄永艳
(山西大学 数学科学学院, 太原 030006)
本文主要考虑下面的Choquard方程[1-9]:
-Δu+u=λ(Iα*|u|p)|u|p-2u+
|u|2*-2u,x∈RN
(1)
其中:N≥3;α∈(0,N);λ>0;p是介于上下临界之间且不包含上下临界的数,上临界是指(N+α)/(N-2),下临界是指(N+α)/N。Iα是一个Riesz势函数,即
若λ=1,且没有临界项,方程(1)是Choquard-Pekar方程:
-Δu+u=(Iα*|u|p)|u|p-2u
x∈RN
(2)
当N=3,α=2,p=2时,方程(2)描述了带电粒子与未知电磁场之间的相互作用,在天体力学、量子力学、统计物理学中都有广泛的应用,可参考文献[4,9]。Lieb[1]和Lion[2]最早证明了方程(2)非平凡解的存在性。目前,已经有一系列关于Choquard-Pekar方程的结果,可参考文献[5]。
Seok[3]用扰动理论证明了下面Choquard方程径向对称解的存在性:
-Δu+u=(Iα*|u|p)|u|p-2u+λ|u|2*-2u
其中x∈RN。最近,Schaftingen等[6]证明了当非线性项f(x,u)=f(u)满足一定条件时,下面Choquard方程基态解的存在性:
-Δu+u=(Iα*|u|(N+α)/N)|u|(α-N)/Nu+f(x,u)
x∈RN
受上述结果的启发,本文研究当λ≥λ0时,Choquard方程(1)基态解的存在性。
定理1存在λ0>0,使得对于所有的λ≥λ0,Choquard方程(1)有一个基态解。
在定理1中得到的基态解是指相应能量泛函的所有非平凡临界点中使能量泛函能量达到最小的那一个,也就是极小化问题
m=inf{J(u):u∈H1(RN){0},J′(u)=0}
(3)
可达时对应的极小值点。
1 准备工作与能量估计
记Lq(RN)中的范数为|·|q,Ck表示不同的正常数,R+=[0,∞)。
工作空间是Sobolev空间H1(RN),它的标准范数是
▽u|2+u2])1/2
H1(RN)连续嵌入Lq(RN),q∈[2,2*]。因此,对每一个q∈[2,2*],存在一个正常数Cq,使得
|u|q≤Cq||u||,u∈H1(RN)
(4)
方程(1)对应的能量泛函是
由Hardy-Littlewood-Sobolev不等式和式(4)知,J在H1(RN)上被很好地定义,并且属于C1。它的导数是
(▽u·▽v+uv)-
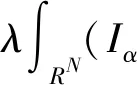
u,v∈H1(RN)
因此,方程(1)的弱解是能量泛函J的一个临界点。下面给出著名的Hardy-Littlewood-Sobolev不等式[8]。
引理1(Hardy-Littlewood-Sobolev不等式) 若s,t>1,μ∈(0,N)满足
则存在正常数C(N,μ,s),使得对于所有的u∈Ls(RN),v∈Lt(RN),有
为了得到泛函J的一个(PS)c序列,需要验证J满足山路结构。
引理2泛函J满足山路结构,即
① 存在r,η>0,使得对于所有满足||u||=r的u有J(u)>0,而且对于所有满足0<||u||≤r的u有J(u)>0。
② 存在u0∈H1(RN), 使得||u0||>r和J(u0)<0成立。
证明
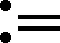
C1t2-C2t2p-C3t2*,t∈R+
所以,
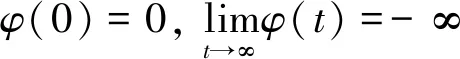
故存在t0>0且t0足够大,使得对于u0=t0u,②成立。
通过经典的山路定理[7],能量水平c0可以刻画为
(5)
其中:Γ={γ∈C([0,1],H1(RN);γ(0)=0,J(γ(1))<1}。
为了确保紧性,现在对能量水平c0给出一个估计。
令S是最佳Sobolev嵌入常数,即

引理3设N≥3且c*=SN/2/N,则c0 证明令 对任意的u∈H1(RN){0},由引理2的②可知,存在tu>0,使得J(tuu)<0。 因此,由c0的定义可知, 于是c0≤c1。为了完成证明,下面只需证明c1≤c*。 令h(t)=J(tu0),t∈R+,则h′(tλ)=0,也就是 进一步得到 注意到,当λ→∞时,有 于是,tλ→0,λ→∞。由h的连续性可知, 因此存在λ0>0,使得对于所有的λ≥λ0,有 于是对于所有的λ≥λ0,有 在这一部分,分两步来证明定理1,首先证明方程(1)在c0 令 引理4如果{un}是H1(RN)中的一个序列且满足 则 证明注意到 再结合S的定义,可得 于是, (6) 因此, (7) 结合式(6)和(7)得到理想结论。 引理5设{un}⊂H1(RN)是J的一个(PS)c序列,则{un}在H1(RN)中是有界的。 证明取μ=min{2p, 2*}>2,由{un}⊂H1(RN)可知J的一个(PS)c序列: c+on(1)+on(1)||un||=J(un)- 于是,{un}在H1(RN)中是有界的。 引理6设{un}⊂H1(RN)是J的一个(PS)c序列,其中c∈(0,c*),则存在平移过的子序列{un}弱收敛到u≠0,而且 J′(u)=0,J(u)∈(0,c] 证明本文断言 事实上,若不成立,则由Hardy-Littlewood-Sobolev不等式可知 *|un|p)|un|p=0 (8) 由〈J′(un),un〉=on(1)可知 *|un|p)|un|p+ (9) 结合式(8)和(9)可得 另一方面,由J(un)→c>0可以得到 于是,由引理4可知 与已知条件矛盾。因此,根据文献[7],存在{un}的子序列,仍记为{un},σ>0和{yn}⊂RN,使得对所有的n, (10) 记vn(·)=un(·+yn)。由J的平移不变性可知{vn}也是J的一个(PS)c序列。通过引理5可知,{vn}在H1(RN)中是有界的, 因此可以假设在H1(RN)中{vn}弱收敛到u,而且由式(10)可知u≠0。 现在证明J′(u)=0。根据文献[9],对任意的w∈H1(RN),有 *|vn|p)|vn|p-2vnw→ 而且 所以J′(u)=0。 取引理5中的μ,可推出 用范数的弱下半连续性和Fatou引理可得 于是J(u)∈(0,c]。 定理1的证明由引理2和山路定理可知,在H1(RN)中存在J的一个(PS)c0序列{un},即 J′(un)→0,J(un)→c0 其中能量水平c0在式(5)中给出了定义。由引理5知,当λ>λ0时,c0∈(0,c*)。因此,通过引理6知,若{un}弱收敛到u,则u是泛函J的非平凡临界点J(u)∈(0,c0]。 下面证明由式(3)定义的极小化问题是可达的。令{vn}是由方程(1)的非平凡解构成的序列,且满足 当λ>λ0时,观察到m≤c0 (11) 所以{vn}在H1(RN)中是有界的。而且由Hardy-Littlewood-Sobolev不等式和式(4)可得: *|vn|p)|vn|p+ 因此, 再结合式(11)知m>0。因为序列{vn}是泛函J的一个(PS)m序列,再次用引理5,可知存在u∈H1(RN){0},使得J′(u)=0,而且J(u)∈(0,m]。另一方面,由m的定义可得J(u)≥m。因此,J(u)=m,即u是方程(1)的基态解。
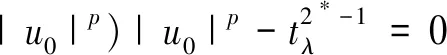
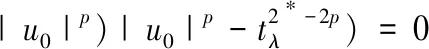
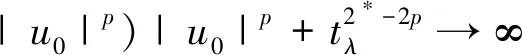
2 定理1的证明