基于ADAMS的串联式6自由度平台仿真分析

邹喜红，王瑞东，涂国杰，梅 亚

(重庆理工大学 汽车零部件先进制造技术教育部重点实验室， 重庆 400054)

串联式6自由度平台是区别于并联式的一种运动机构。相对于并联式而言，它具有精度高、刚度强、稳定性好、可达空间位置广阔等优点，在汽车领域和航天、航海领域得到密切关注，很多企业投入大量资金进行研发。因此，为了降低平台的研发成本，缩短设计和优化周期，对其进行仿真分析是必不可少的一个环节[1-3]。

运动学与动力学仿真软件有很多，如ADAMS、solidworks、Matlab等。本文以串联式6自由度平台为研究对象，在ADAMS中建立仿真模型，充分发挥ADAMS Motion模块的仿真功能，对模型进行运动学与动力学仿真，包括对作动器位移、速度、加速度运动特性的分析以及驱动力、扭矩动力特性的分析。该方法提高了工作效率，节省了研发时间，并为后续的优化和控制提供了参考，同时为电池包等汽车零部件道路模拟试验提供了条件。

1 串联式6自由度平台结构与原理

串联式6自由度平台是一种具有6自由度运动能力的机构。如图1所示，平台主要包括：① 动平台，用于承载负载(被试件)；② 液压作动器，共6个，用于实现驱动；③ 转动块3个，用于实现运动换向；④ 连杆3个，用于连接动平台与转动块；⑤ 铰链，包括6个球铰、6个虎克铰，用于固定连接两个构件；⑥ 静平台，即机构的底座。该串联式6自由度平台通过6个液压作动器的伸缩来实现横移、纵移、升降、横摆、侧倾、偏航6个自由度的运动以及它们的组合运动。

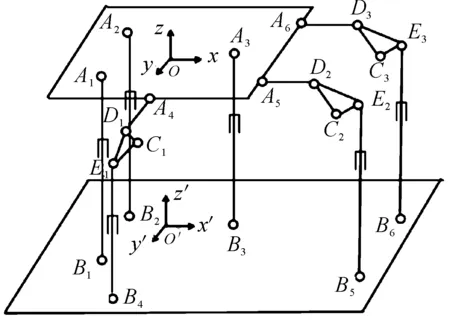
图1 串联式6自由度平台简图

2 串联式6自由度平台三维建模

2.1 ADAMS三维模型

在ADAMS/View模块中建立6自由度平台三维实体模型，建模过程主要分为以下3步：① 在菜单栏下设置工作栅格、坐标系和单位；② 根据平台各部件的外形尺寸运用几何建模工具箱进行各部件的实体建模；③ 以静平台为基准，依次根据装配关系完成静平台、动平台、作动器、转动块、球铰等部件的装配。完成的三维装配模型如图2所示。

图2 三维装配模型

2.2 ADAMS环境下添加约束和驱动

本文采用6个作动器来控制6个方向的运动，根据Kutzbach Grubler公式可知：

式中：F为机构自由度；n为构件总数(包括机架)；m为运动副；fi为第i个运动副的自由度。

从平台的三维模型中可以看出：垂直方向(z轴方向)有3个作动器，作动器底部与静平台用虎克铰连接，头部与动平台为球铰接触；横向(x轴方向)有1个作动器，纵向(y轴方向)有2个作动器，作动器头部通过转动块与连杆连接，底部与静平台为铰链接触；连杆与动平台为球铰接触，与转动块为虎克铰连接。根据机构的等效原理，对横向和纵向的作动器进行简化，简化结果如图3所示。

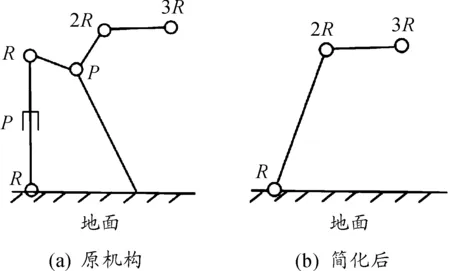
图3 机构简化

移动副、转动副具有1个自由度，虎克铰副有2个自由度，球铰副有3个自由度，构件数为14个；运动副共有18个，包括3个转动副、6个虎克铰副、6个球铰副。由于简化后的模型不存在过约束和冗余结构，所以机构的自由度为

在ADAMS/View环境下，运用运动副工具箱按照平台要求依次添加所需运动副。ADAMS会根据构件数量、运动副类型以及所加驱动的类型和个数对机构的自由度进行验证，结果会在信息窗口显示。从图4中可看出，经过ADAMS模型检查以后，机构的自由度为6，所添加的运动副与理论吻合。

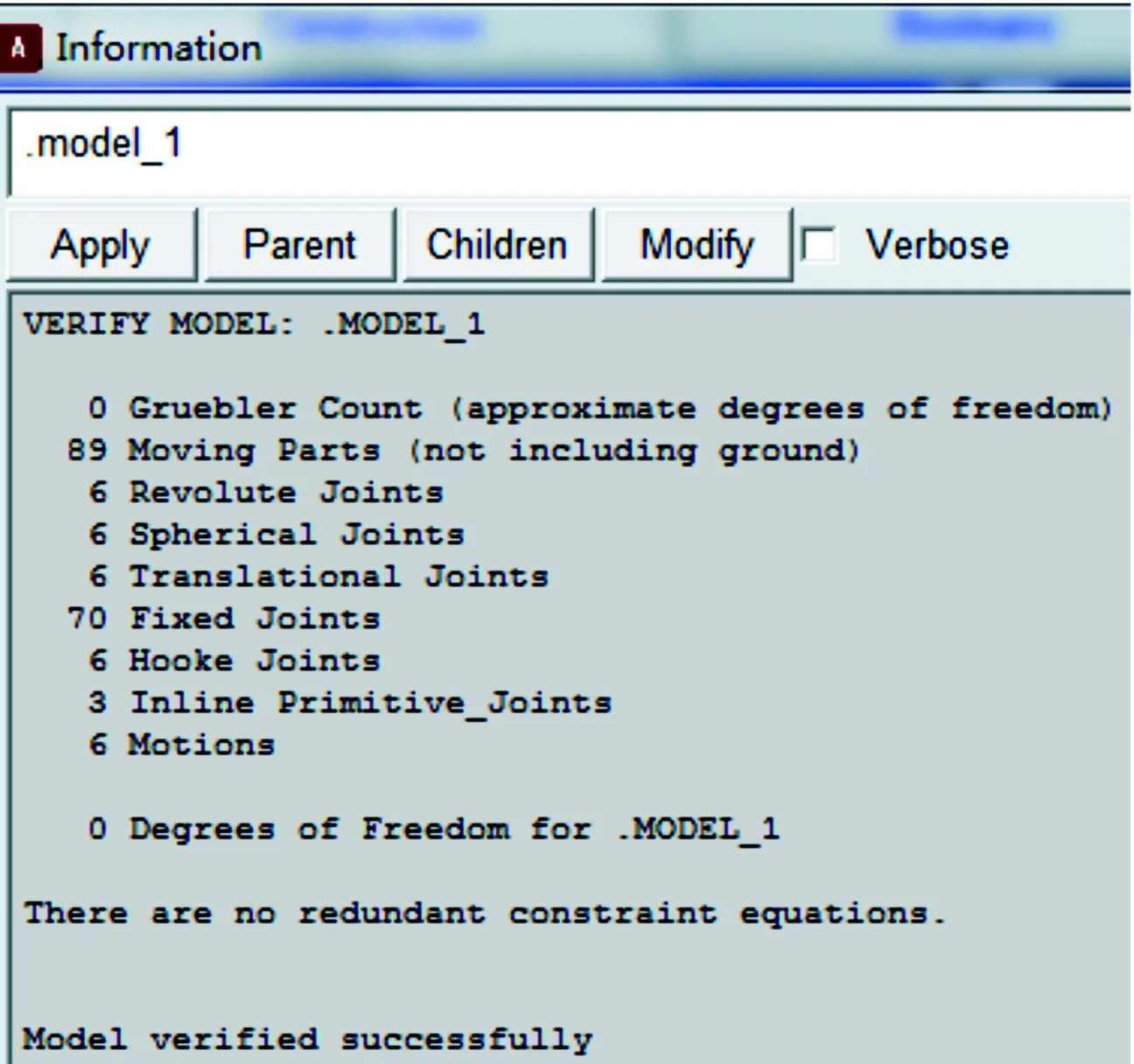
图4 ADAMS添加约束驱动后的信息窗口

3 串联式6自由度平台运动学仿真

为了对串联式6自由度平台的运动特性进行分析，给定动平台一移动和转动并存的位姿，在ADAMS环境中分析其运动特性及极限位姿。

让动平台先沿x、y、z轴3个方向平动，再绕x、y、z轴转动，分析动平台与作动器的运动情况。运动位姿参数见图5。

3.1 动平台的运动特性

动平台的运动情况直接决定了被试件的运动轨迹，故其运动特性也决定了被试件的运动特性。

由图6、7可知：动平台位移曲线在10～15 s内呈上升趋势，而在0～10 s和15～30 s内保持不变，这是因为在x、y方向的平动不影响动平台幅值，只是绕着坐标轴转动，幅值不发生改变；速度、加速度曲线在15～30 s以及角速度、角加速度在0～15 s内也保持不变，这是因为动平台的转动有的只是角速度与角加速度，跟速度与加速度无关；各曲线整体波动比较平稳，无异常点。因此，动平台的运动特性曲线基本都反映了真实的运动情况。

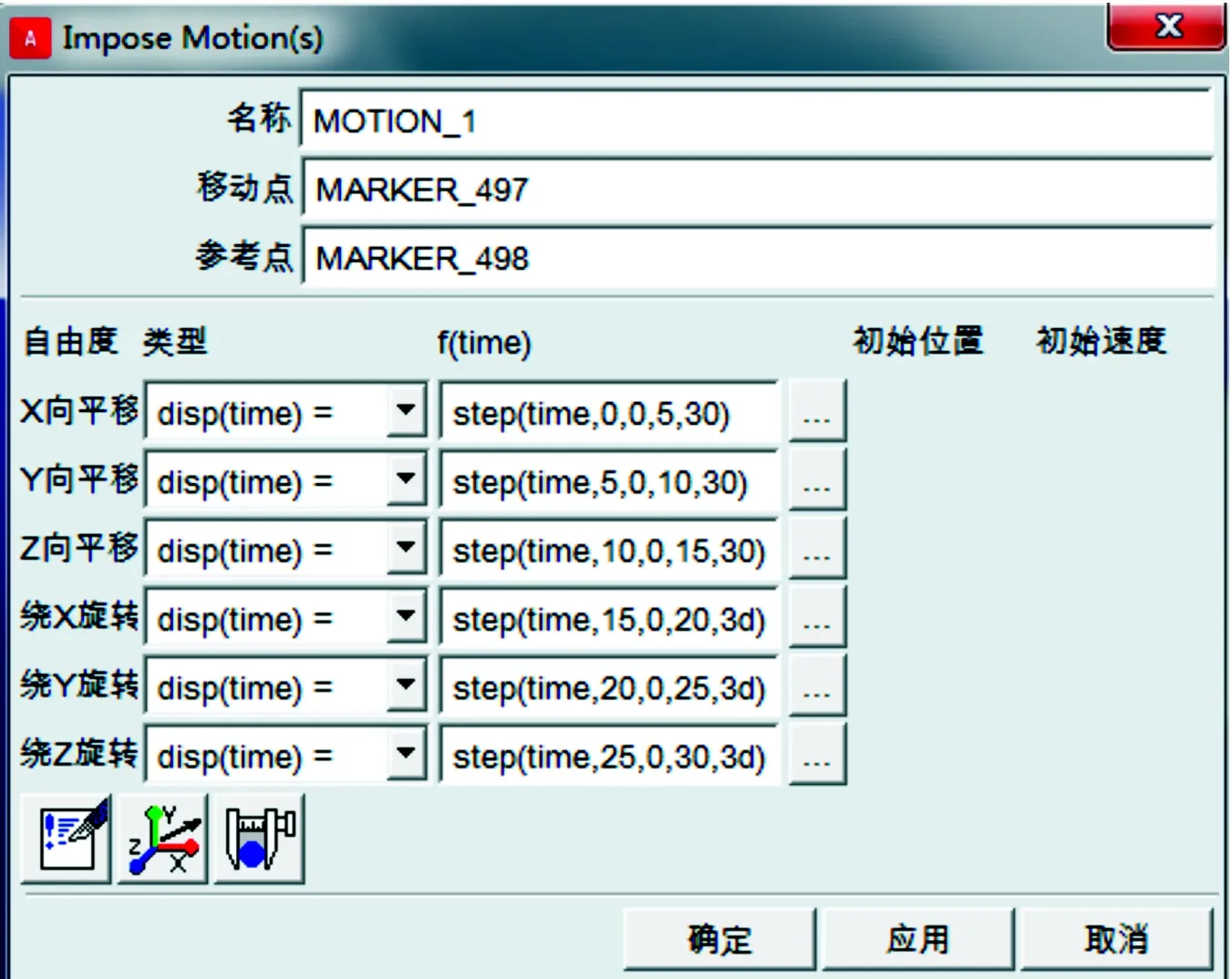
图5 运动位姿参数

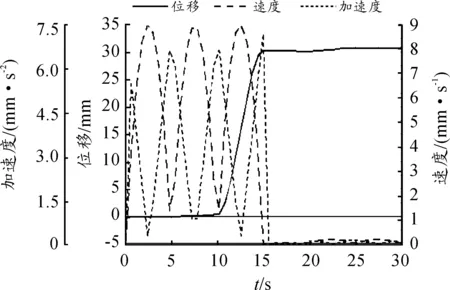
图6 动平台位移、速度、加速度曲线

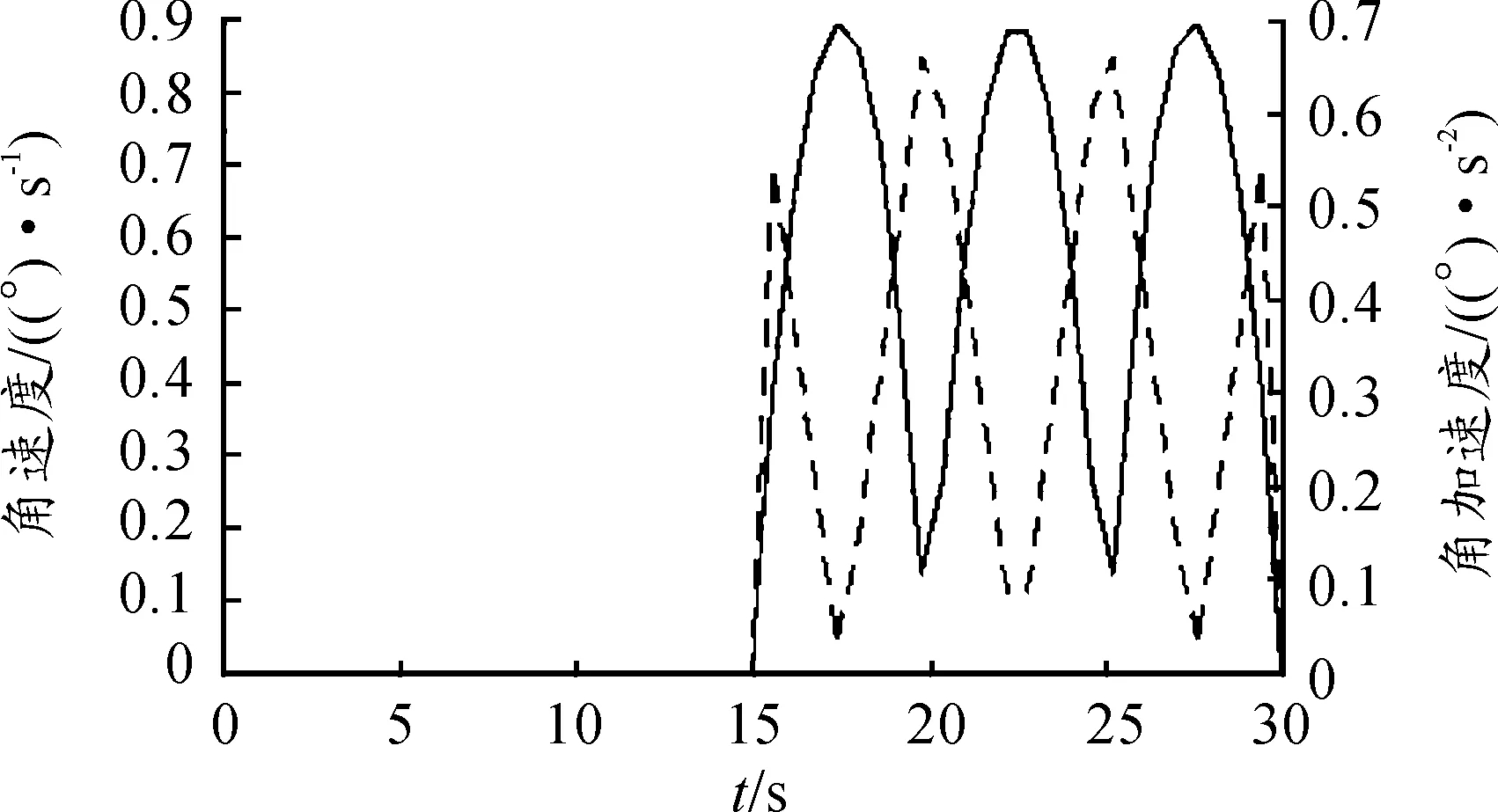
图7 动平台角速度、角加速度曲线

3.2 作动器的运动特性

作动器运动特性最直接的表达就是其长度、速度、加速度的变化。由图8可知：1、2号作动器变化趋势相同，5、6号作动器变化趋势互补，与3、4号作动器变化趋势有明显差异。出现这种情况的主要原因是作动器分布位置不同以及初始位置的差异使得动平台在移动后出现各个作动器伸缩量不同造成的，这是不可避免的一种差异。x、y、z三个方向的平动中，z方向的平动作动器伸缩量最大；x、y、z三个方向的转动中，y方向的转动作动器伸缩量最大。

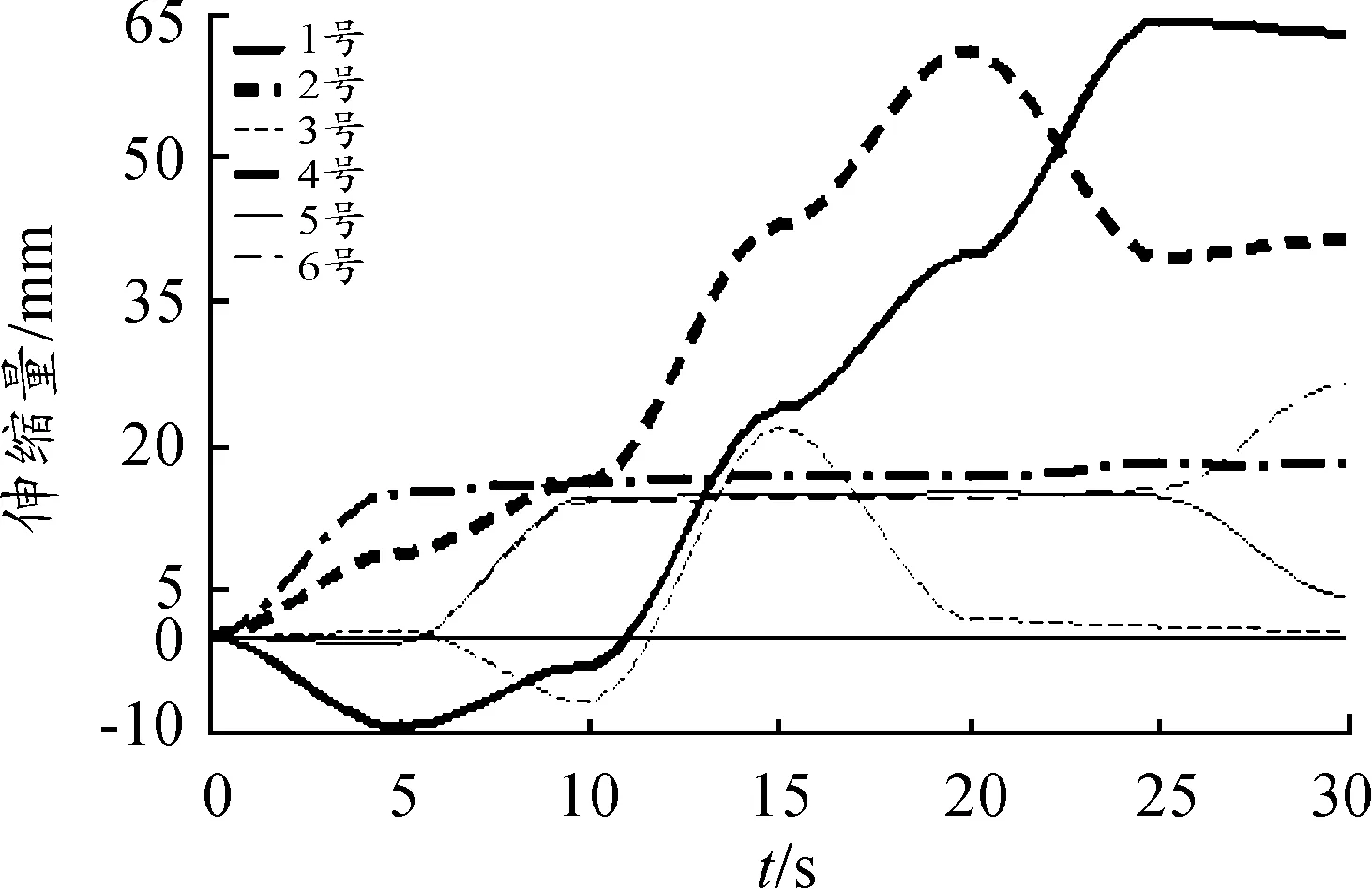
图8 作动器伸缩量曲线

由图9、10可知：各作动器速度、加速度运动情况基本一致，曲线整体波动比较平稳。x、y、z三个方向的平动中，z方向的平动作动器速度、加速度最大，x、y、z三个方向的转动中，y方向的转动作动器速度、加速度最大。

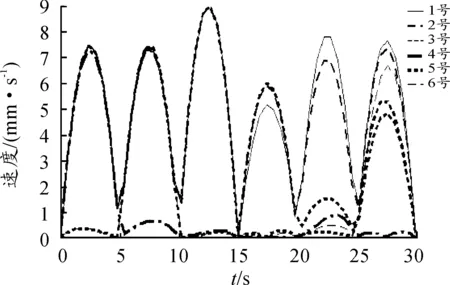
图9 作动器速度曲线

图10 作动器加速度曲线

3.3 动平台的极限位姿

在ADAMS View模块定义测量函数，同时布置传感器分别对作动器进行位移限制和对球铰、虎克铰进行角度限制。给定动平台一大位姿，当位移和角度超限时仿真停止，仿真停止信息窗口见图11。

图11 仿真停止信息窗口

根据仿真结果可得：该平台x方向所能达的最大位移为70 mm，y方向所能达的最大位移为72 mm,z方向所能达的最大位移为90 mm；x方向所能转动的最大角度为10°，y方向所能转动的最大角度为9°，z方向所能转动的最大角度为12°。

4 串联式6自由度平台动力学仿真

4.1 作动器的动力特性

动平台在运动过程中，其动力特性决定着运动的输出效果，作动器动力特性主要体现在所受力跟扭矩的变化。

对所设计的串联式6自由度平台各构件施加负载，观察在一定载荷作用下，当动平台在做位姿变化时，各作动器所受力跟扭矩变化是否平缓，所受力的大小是否符合要求。

由图12～14可知：各作动器驱动力变化均比较平缓无毛刺；当给定动平台某一位姿变化时，3号作动器所需驱动力最大；x、y、z三个方向的平动中，z方向的平动所需驱动力最大；x、y、z三个方向的转动中，y方向的转动所需驱动力最大。

由图15可知：3号作动器所受扭矩最大，4～6号作动器次之，1、2号作动器所受扭矩最小。这是因为转动块的作用增大了4～6号作动器的扭矩，而3号作动器扭矩最大是因为它承担了动平台大部分负载的缘故。x、y、z三个方向的平动中，z方向的平动所需作动器扭矩最大；x、y、z三个方向的转动中，y方向的转动所需作动器扭矩最大。各作动器扭矩曲线都比较平缓，基本能够反映真实情况。

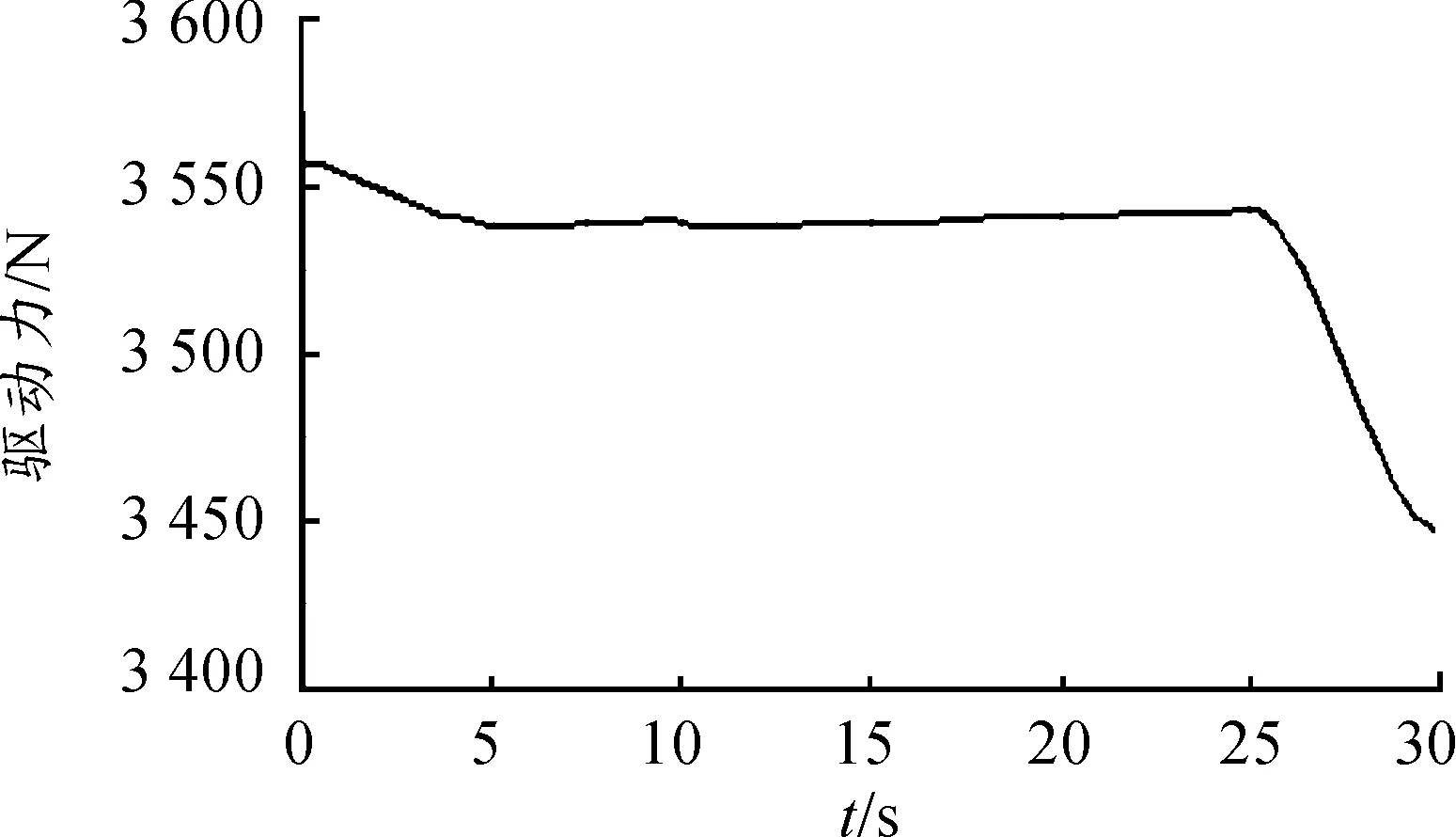
图12 1,2号作动器驱动力曲线

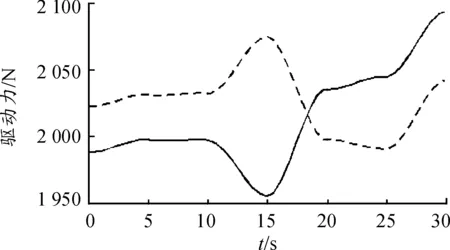
图13 3号作动器驱动力曲线

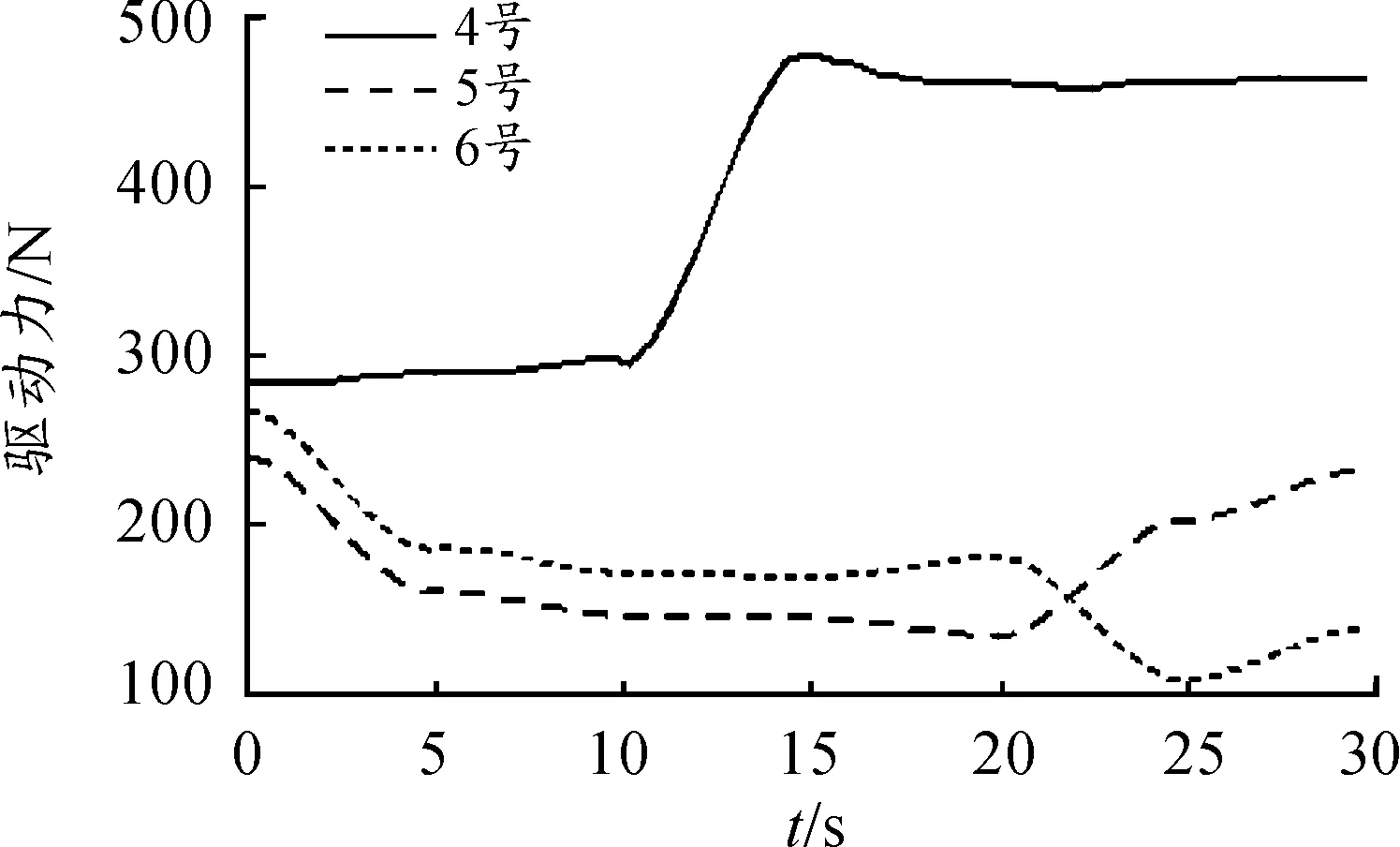
图14 4～6号作动器驱动力曲线

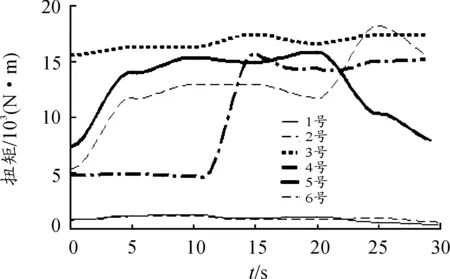
图15 各作动器扭矩曲线

4.2 动平台的极限载荷

对动平台施加载荷，把它简化为在动平台质心处施加一垂直向下的力，给定动平台一位姿，通过改变力的大小来分析该平台所能承受的最大载荷。因为动平台在运动过程中，3号作动器所受力最大，所以在这里以3号作动器为研究对象。

由图16可知，当施加48.9 kN的载荷时,3号作动器的最大驱动力可达24.96 kN,趋近于作动器的最大激振力25 kN，所以此平台所能承载的最大载荷为48.9 kN。

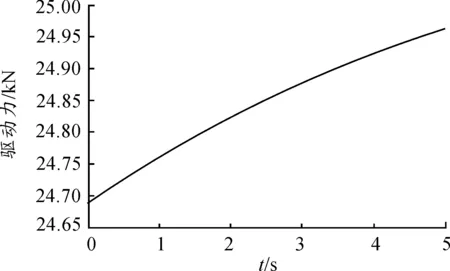
图16 3号作动器极限驱动力曲线

5 结束语

本文运用ADAMS软件对串联式6自由度平台在6个方向的位姿进行了运动学和动力学仿真，分析了在不同位姿驱动下各作动器运动参数和动力参数的变化规律以及极限位姿和载荷，结果表明：① 在不同位姿驱动下，z方向的平动和y方向的转动所需作动器伸缩量、速度、加速度、驱动力和扭矩最大，平台的运动特性和动力特性曲线都比较平缓无毛刺，基本能反映真实情况；② 该平台所能达的最大位姿为(70,72,90,10,9,12)，高于电池包在实际路面的最大振动位姿，最大载荷为48.9 kN，也远高于电池包的重力5 kN。本文仿真结果为后续的优化和控制提供了重要的参考，同时为电池包等汽车零部件道路模拟试验提供了一种方法。