多段式拖曳系统低张力缆段隔振方法研究

王志博

(江苏科技大学,江苏 张家港 215600)

拖曳系统工作于多种海况下，风浪流等扰动源对拖曳系统的探测精度和准确度造成了极大影响[1]。在设计可搭载声学、光学、电磁等多样化的探测系统的拖曳系统过程中，抵抗复杂海况的扰动维持拖曳系统的运动稳定性成为了拖曳系统设计中的主要目标[2]。两段式和多段式的拖曳系统，从母船到沉降器的缆段部分处于高张力水平，缆内的高张力增强了扰动传递的速度频率，可将这一段缆看成轴向高刚度而阻尼极低的结构，扰动几乎无衰减的从水面传递到沉降器[3]。在沉降器之后是低张力缆段，张力降低了，那么缆对扰动传导作用下降，阻尼增强。所以张力水平的下降能够增强缆对扰动传递的阻尼效应，这是多段式拖曳系统设计的基本思想。然而拖曳缆对运动传递的阻滞作用不仅与缆内张力水平的高低变化有关，而且与拖曳系统各缆段的长度、浮态等参数有关，应当从增强拖曳系统的阻尼水平的角度出发来分析这些参数对提高拖曳系统抵抗扰动传递的能力的影响。

为了模拟多段式的拖曳系统动的运动响应，典型的拖曳系统动力学的模拟方法可分为集中参数法[4-5]、有限元法[6-7]、有限差分法[8-9]。由于集中参数法将缆受到的分布力集中到有限的节点上，从节点受力分析的角度建立动力学方程组，没有针对缆的阻尼性质的建模。在有限元方法建模中采用便于数值处理的瑞利阻尼，瑞利阻尼模型与拖曳缆实际运动阻尼也存在很大差别，甚至无法考虑高张力对扰动传递的增强作用。

基于有限差分法的Ablow动力学模型中水动力阻尼与结构参数等高度耦合，无法剥离出专门描述拖曳系统阻尼的模型，在动力学模型中起到阻尼行为的缆索运动状态，常常与缆的刚度和空间变形高度的耦合在一起，这使得拖曳系统的空间操纵运动反映出多样化的非线性的阻尼行为[10-12]。

本研究着重研究多段式拖曳系统中的阻尼隔振特性，去掉多段式拖曳系统中水面端至沉降器的极低阻尼的缆段，截取其中的第二段缆以及以下的缆段进行模拟，将第二段缆的起始部分简化为强迫振动源，利用阻尼增强设计方法设计这些缆段，计算干扰运动受到的阻滞和衰减作用。本研究一方面对阻尼在拖曳系统的分布特性进行分析；另一方面对Ablow的动力学模型进行改进，借助数值手段对低张力拖曳缆与拖曳体，以及加装了阻尼单元的多段式拖曳缆进行系统的计算对比，获得系统的隔振效应。

1 拖曳系统动力学模型

拖曳缆系统由缆和拖曳体构成，在将缆简化为柔性的细长的光滑圆柱的基础上，通过拖曳缆上任意一点的受力状态的分析，考虑了缆受到重力、浮力、张力、流体作用力、附加质量力，Ablow将拖曳缆的动力学方程组写成

(1)

待求解变量Y包括缆的张力T和运动速度(vt,vn,vb)以及缆的倾角θ和扭转角度φ。

Y=[Tvtvnvbθφ]T

(2)

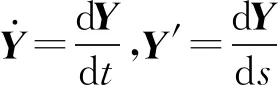
结构变形矩阵M的结构为

式中：e为缆的轴向应变；ρ为水流密度；A为缆的横截面面积；m为单位缆长的质量；m1为缆的附加质量；(Jb,Jn)为缆的切向和副法向的水流速度。

非定常矩阵N为一个结构质量、刚度、阻尼行为高度耦合的矩阵，该矩阵为一个上三角矩阵

水流阻尼矩阵

本研究认为Ablow将拖曳缆简化为柔性缆不考虑弯矩扭转作用，同样拖曳体也不考虑转动自由度，这对缆传递扰动并无实质影响，在全局坐标系O-XYZ中，采用质点动力学模型模拟拖曳体和阻尼器的运动

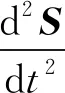
(3)

其中,

S=[XYZ]T,F=[XFYFZF]T。

式中：m0为拖曳体的质量；Cmax,Cmay,Cmaz为拖曳体的附加质量系数；(X,Y,Z)为全局坐标系下的拖曳体的运动；XF,YF,ZF为拖曳体受到的力；LX,LY,LZ为拖曳体的流体动力特征长度；mg，ρgV为拖曳体的重力和浮力；如图1所示全局坐标系与随体坐标系的变换关系为欧拉变换

(u,v,w)=(U,V,W)[R]

(4)

图1 拖曳缆元的坐标系变换Fig.1 Coordinate transformation of towed cable segment

如图2所示，单体拖曳系统由母船-缆-拖曳体组成，是典型的高刚度低阻尼拖曳系统，对于这类拖曳系统的动力学模型，可借助有限元方法结合瑞利阻尼模型，能够较好的近似拖曳缆的阻尼特性，但是随着放缆长度的增大，由于缆的空间弯曲效应形成的阻尼比重会有所增强，仅仅采用简单的瑞利模型则不能准确获得低张力缆段在高水平阻尼作用下的隔振性能。在多段式拖曳系统中由于缆内张力并不连续变化，缆内张力下降的同时阻尼水平也随之增加，根据拖曳系统阻尼行为的形成原因，可把阻尼分成三部分:

(1)缆张拉状态对应的结构阻尼；这部分阻尼随着缆倾角和扭转角的增加而增大;

(2)水流阻尼，水流阻力这一分布力增大了缆倾角和扭转角度,当缆径与来流方向，水流阻尼和很快衰减横向振动的传递;

(3)空间运动阻尼，包括倾角和扭转角度阻尼项，空间倾角将部分沿着轴线传递的扰动转换为沿着径向的扰动传递。

图2 多分段拖曳缆阻尼分布特性结构图Fig.2 Damp level of multi sections towed cable

依据Wu和Wang等给出的有限差分盒式离散格式求解上述方程式(1)，该离散格式将缆离散为缆段长度为ΔSj长度的n(j=1,2,…,n)段缆，时间推进步长设为Δti(i=1,2,…，n)，在缆段的中点节点处ΔSj+1/2以及时间节点Δti+1/2处应用差分关系式可得到

(5)

该数值方法的程序编制在本研究的前期研究基础上已经完成(参见Wang等的研究)，进行了系统的比较验证，并应用到了数值计算拖曳缆操纵运动响应运动的研究中。

由于低张力缆的初始条件下，缆轴线与来流平行，初始状态下Q1,5与Q1,6均为零，这种情况下容易引起数值求解器不稳定，引入一个微小的缆初始倾角θb，从而使缆处于略有迎流，这种情况下可克服初始缆形求解趋于发散的现象。强迫振动源设计为缆端的强迫位移，服从正弦规律的强迫振动

X0=0,Y0=0,Z0=A0sinωt

为便于比较，本研究中的振动源的振幅设定为单位振动，幅度为A0=1 m，振动周期为

对应的振动速度为

u0=0,v0=0,w0=A0ωcosωt

利用式(4)给出的欧拉角转换将缆端强迫振动换算到拖曳缆的随体坐标系中。

2 扰动传递的能量衰减定性模型

沉降器处的强迫振动视作振动源，悬挂体I和II的设计目的是起到阻尼作用，以致强迫扰动的传递可快速消减，而尾端连接的拖曳体将保持平稳航行。从拖曳体的水动力性能角度来看，降低拖曳体航行阻力将降低牵缆力，进而由缆在空间振动降低传递而来的扰动作用。

图3 缆的径向和轴向迎流效应的差异Fig.3 Cross flow at axial and radius motion

缆的轴向(横截面的法向)迎流和缆的径方向的迎流状态相比而言具有完全不同的流动特征。比较两个方向的流动效应拖曳缆的水流作用力成分可知，沿着轴向的流动阻力以摩擦阻力为主，而沿着径向的流动阻力以压差(漩涡)阻力为主。因而轴向的水流阻力远比径向的阻力要小，缆在传递扰动的过程中，发生了小幅度的径向振动运动，振动速度越大，水流阻力越大，因此缆的振动降很快被水流阻力衰减，所以低张力缆段空间缆型要保持成为近似水平缆型。缆受到了水流阻尼力、缆内张力取决于水流阻力和尾端悬挂的物体的水流阻力。若不考虑缆内张力的张拉作用，假设振动源传递而来的径向的激振为规则正弦激励

P=P0sinωt

式中：P0为扰动幅；ω为扰动频率，拖曳缆上任意一点的横向响应运动位移为

x(t)=Bsin(ωt-φ)

式中：B为振幅；φ为相位差。

对应的扰动速度为

对应的水流阻尼力为

式中：Cf为水流阻尼力系数，那么缆上任意点上的扰动力合力做功W写成

(6)

由P0sinωt=P0cosφsin(ωt-φ)+P0sinφcos(ωt-φ)代入式(6)计算积分整理可得

缆上当地点受到的水流作用力对扰动的消减比率为

(7)

由式(7)可知，缆的当地密度越大，沿着横向振动的方向的阻尼力系数C越大，那么对扰动的消减效果越好，而且扰动的频率越大，扰动消减的越迅速。因此在设计中应当注重引入阻隔横向振动的阻尼器抵抗扰动和改变运动频率，但是要注意到额外的水中重量增大的设计不应引起缆内张力的增大。

3 低张力缆+拖曳体振动传递响应特性

3.1 单段低张力拖曳缆的强迫扰动的传递规律

根据式(7)给出的分析，横向阻尼可起显著隔振效果。以某二段式的拖曳系统中的水下低张力脐带缆的运动进行建模，该缆段将沉降器的受迫振动简化为点源扰动，第二段缆的结构参数见表1，对拖曳系统设计采用阻尼增强型设计方法，尽可能增加水动力阻尼对振动的衰减效应，同时多次改变运动传递的路径。如表1所示选用水中中性的脐带缆、阻尼单元、拖曳体，以维持低张力状态下的水平漂浮状态；采用圆柱水流阻力系数计算缆的水流阻力；由于扰动以Z向升沉运动传递而来，通过增大阻尼单元的垂向阻尼系数Cmaz来考查对扰动隔振效果，如将缆的尾端拖曳体的垂向阻尼增大到阻尼单元质量的5～1 000倍。为了考察阻尼单元的布置方式对隔振效果的影响，如表1所示设置了四种布置阻尼单元的方式，尾端拖曳体的阻力决定了整个缆段的张力大小，采用流线型设计得到较小的拖航阻力系数CX。

首先采用缆+尾端拖曳体的形式，模拟低张力缆不加装任何阻尼单元的运动传递。改变拖曳缆的长度，分析扰动传递的规律，随着缆长度的增加，缆发生横向振动传递的周期性振幅增多。缆受到的横向扰动的阻尼增强。这种抵抗扰动的效应降随着缆长度的增加而逐渐递减。基于表1给出的脐带缆长度在小于500 m的范围内，取不同长度的缆长计算扰动的传递。并设置不同的拖曳体阻力系数和拖曳速度，使缆内张力处于不同的水平。对比图4中的不同的缆长但同一个拖曳速度下的运动传递至尾端的情况可知，随着缆长的增大，扰动的周期增大，幅度减小。这说明随着缆长的逐渐增加缆对扰动的传递周期逐渐增大，扰动衰减趋向于平缓，阻尼效果逐渐增强，例如当缆长增加到500 m时，扰动幅度迅速衰减成为微幅扰动。而在同一个缆缆长情况下，由于拖曳速度增大，张力逐渐增大，拖曳缆对扰动的传递造成了不同的逐渐减小的周期和逐渐增大的振幅。同一个缆长随着张力和拖速增大，拖曳缆扰动周期略有减小但是幅度却增大。

表1 阻尼型脐带缆参数表Tab.1 Damp enhanced umbilical cable parameters

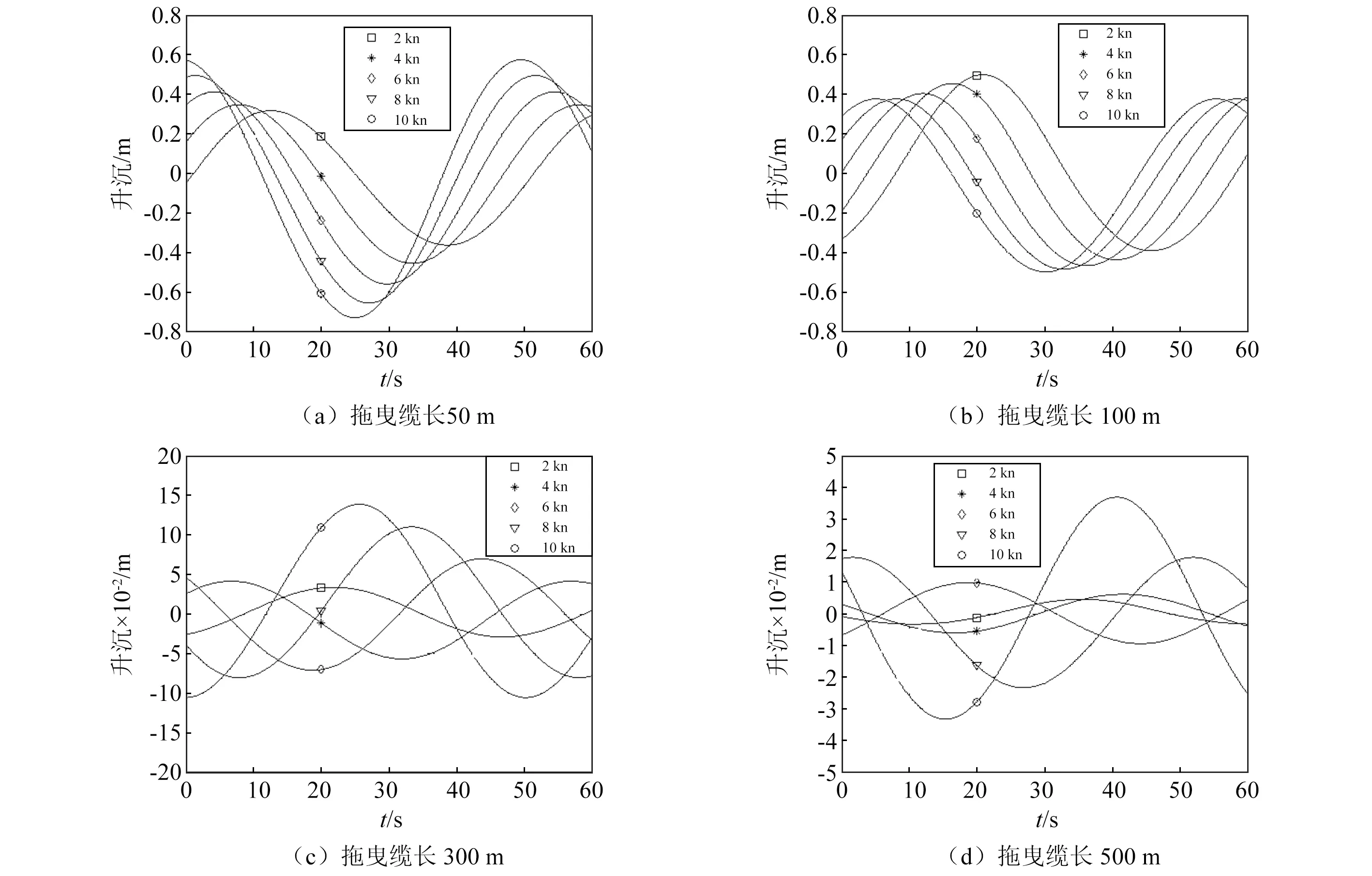
图4 缆长与缆内张力变化对扰动传递的衰减规律Fig.4 Tensional vibration transfer along with cable length

图5给出了不同拖曳速度下传递到拖曳体端的扰动幅与振源处的扰动幅的比，对比可知，振动幅的衰减与缆长并非呈现完全的线性关系，对于表1中给出的拖曳缆结构参数，较小的缆长度(<200 m)在低张力状态下存在共振响应峰值，而后随着拖曳速度的增大，沿着径向的振动逐步减小。但是随着拖曳缆长度的继续增大，这种共振效应逐渐消失，值得注意的是由于图4显示的仅采用了有限的几个拖曳速度，仅能说明共振张拉状态在4 kn附近。

图5 不同拖曳速度下扰动幅度比例的衰减Fig.5 Heave amplitude ratio along towing velocity

实际拖曳工程设计中，常常因搭载探测设备的调整带来拖曳体的净浮力，这会使缆的牵拉角度有所变化，这对振动传递造成了一定的影响。图5给出在[±30%]质量范围内调整拖曳体的水中质量，但不改变拖曳体的浮力，这使得拖曳体分别处于重载和轻载的状态，那么拖曳缆绳的牵缆角度不同，横截面的流体阻尼效应也会随其变化，由于缆重的作用，重载和轻载状态对应的阻尼效果应当略有区别。图5显示出这两种状态下，扰动传递的幅度均有所增加，这是由于扰动沿着缆的传递是以缆轴为基准的横向振动，微幅的空间倾角造成了拖曳体的重力与缆内张力存在的夹角增大，扰动传递而来将继续增大该夹角，造成了缆端拖曳体需要较大的回复运动历程。

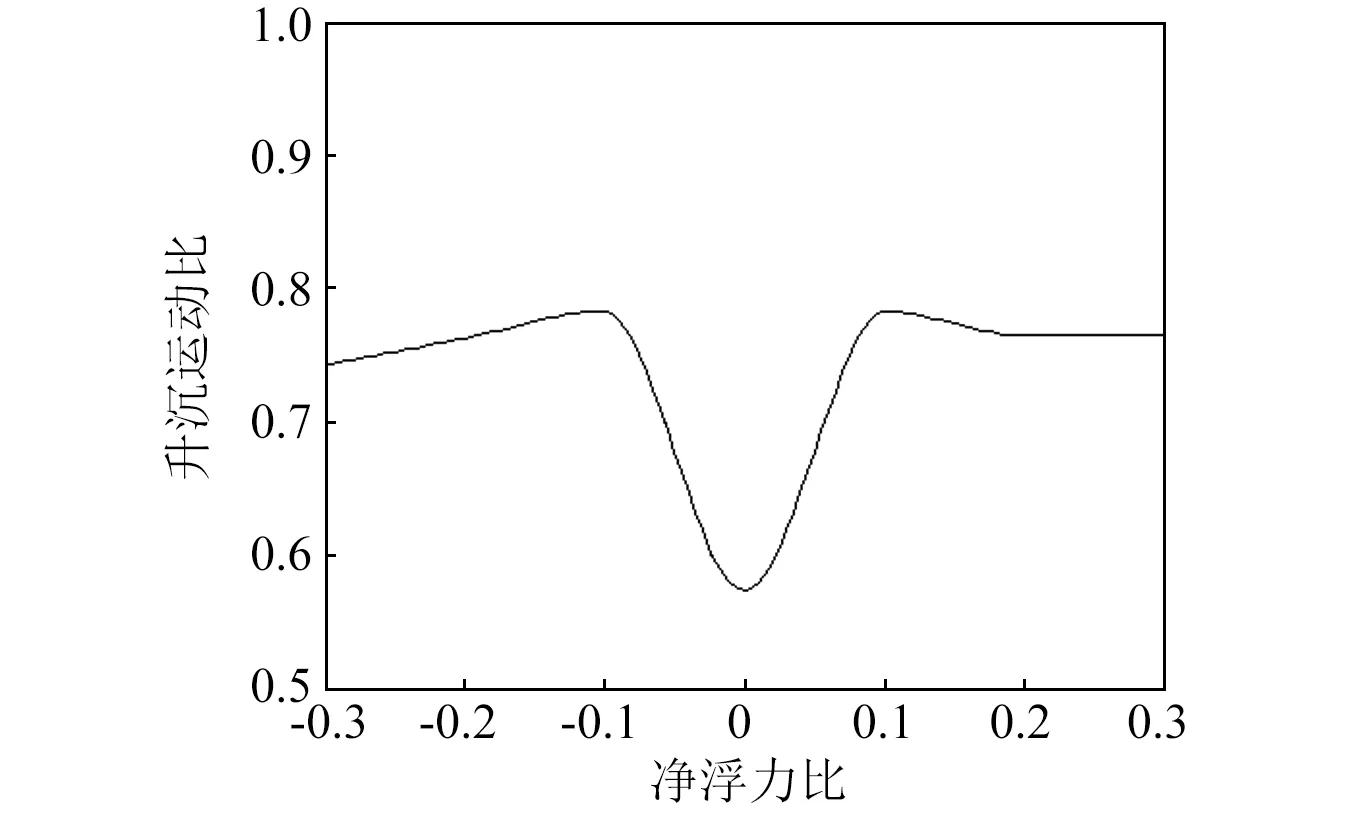
图6 50 m拖曳缆对应的拖曳体浮力变化对牵拉角度的影响和扰动传递的影响Fig.6 Vibration transfer along with buoyancy leading incline angle in a 50 m towed cable system

3.2 改变拖曳体的质量与附加质量与水流阻力

仍以50 m的拖曳缆为例，从图7可知，升沉方向的附加质量过大，这会造成不同阻尼水平的振动响应，拖曳体垂向的附加质量Cmaz分别达到10～1 000倍。依据附加质量的水平不同，运动响应逐渐变换为附加质量特性形成的过阻尼、临界阻尼、和欠阻尼运动。如图7所示低附加质量水平下，拖曳系统处于欠阻尼状态，随着拖曳体的附加质量的增大。由图7可知，垂向附加质量系数的增大使得拖曳体的升沉幅度逐渐增大，运动周期也逐渐增加，但是增加拖曳体的垂向附加质量会增大拖曳缆内张力，这与图4给出的张力增大升沉幅度也增大的规律是一致的，但是附加质量水平改变了强迫振动传递周期。图8给出的超调量随附加质量水平的变化，表明了附加质量可抑制振动的临界阻尼，进入另一个阻尼响应系统特性，本研究称之为第二阻尼状态。

a)欠阻尼状态

拖曳体垂向的分量较小，maz与拖体质量相当时，缆体系统显示出缆与拖体的高度耦合，呈现了低阻尼系统对扰动源的响应状态；

b)第二阻尼状态

在附加质量继续增加的情况下，拖曳体对振动的阻滞效应增强，对传递而来的扰动，出现了一个低频长周期响应，并且扰动的幅度减小，对扰动的抑制效应增强，但是仍然具有两个响应频率，随着附加质量的进一步增大，拖曳系统的响应逐渐进入了另一个长周期的响应运动。

图7 拖曳体不同附加质量系数情况下抵抗扰动的情况Fig.7 Vibration resistance of different towed body added mass

图8 拖曳体不同附加质量水平造成的振动响应超调量分布Fig.8 Heave overshoot along with added mass of towed body

4 扰动传递阻尼设计与传递特性计算

在缆与缆端的拖曳体之间增加水动力阻尼器的设计应当强调阻尼对升沉运动的阻尼作用，并且尽量减小附加质量作用，但是不能显著的增大缆内张力或对其它自由度产生耦合影响。对于多个阻尼器的排布，可通过调整重力和浮力，进而改变空间牵缆角度，进一步增加缆对阻尼作用。但是间隔设置过小，形成直线的牵拉状态。依靠重力和浮力形成不同的牵缆角，间隔设置增大缆呈现出因水流作用而出现的弯曲状态。

表1给出了阻尼器的相关参数，在设计中均采用了低附加质量和高水流阻尼的设计，如图8显示了三种通过设置阻尼器将缆划分为二～六段在定常拖曳情况下的空间缆型。随着增加阻尼单元的增多，拖曳缆沉降效应增大。图9显示了拖曳系统的张力阶跃情况，阻尼器布置数量越多，首段的张力水平越大，那么该段拖曳缆的阻尼水平降低，对振动的阻滞作用减小，但尾段张力仅仅取决于拖曳体的阻力大小。

由图10可知，并非阻尼器越多对振动的隔离效果越好，缆内低张力的尾端要保持适当的长度对振动的阻隔效果显著，如图11所示；缆段的增多只是改变了振动传递的相位。但不能改变缆传递而来的周期。

图9 多分段设置静态缆型Fig.9 Static cable shape of multi cable sections

图10 加装阻尼器的100 m缆长对应的缆内张力分布Fig.10 Tension in 100 m cable with damp units

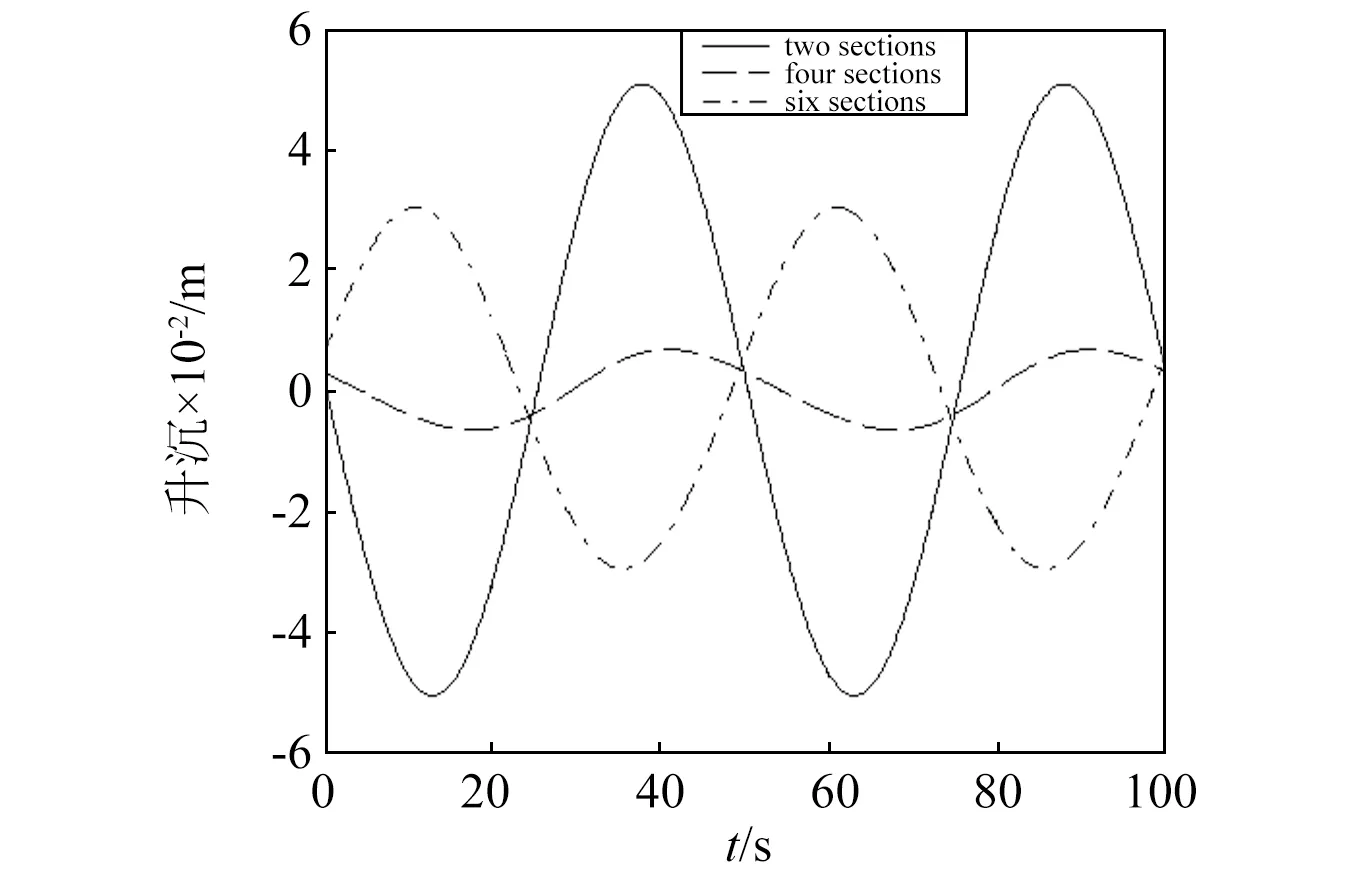
图11 不同阻尼器布置的振动传递周期与微小幅度Fig.11 Vibration period and micro amplitude transfer of different numbers of damp units

5 结 论

将多段式拖曳系统，通过改造Ablow的数值模型，增添了描述阻尼单元和尾端拖曳体的模型，并对初始条件进行了改进。在此基础上对受迫振动下的低张力缆+阻尼单元+拖曳体的运动响应，增加缆的长度将显著的改善隔振效果，适当增大尾端拖曳体的附加质量，可显著的改变运动响应，但是若附加质量设计过大，能抑制扰动源的响应频率，但是引入了与尾端缆长与附加质量另一类长周期振动响应。含有阻尼器的多段式设计中要保持一定长度的低张力缆段，否则会有相反的效果。