应用混合单元基光滑点插值法的声固耦合分析
2019-06-13陈泽聪陈毓珍何智成张桂勇王海英
陈泽聪,陈毓珍,何智成,张桂勇,4,5,王海英
(1.大连理工大学 船舶工程学院 辽宁省深海浮动结构工程实验室,辽宁 大连 116024;2.中国船舶工业集团 上海船舶研究设计院,上海 201203;3.湖南大学 汽车车身先进设计制造国家重点实验室,长沙 410082;4.大连理工大学 工业装备与结构分析国家重点实验室,辽宁 大连 116024;5.高新船舶与深海开发装备协同创新中心,上海 200240;6.大连海洋大学 航海与船舶工程学院,辽宁 大连 116023)
结构在受到载荷激励的时候,会产生振动,同时通过压缩附近的流体介质向周围声场辐射噪声,而声场声压的变化反过来又会激励结构的振动,形成结构与声学介质相互作用的结构声振耦合系统。在汽车、船舶和飞机等结构体的振动噪声分析中,基本都涉及到结构和声学介质的相互作用,所以声固耦合系统的研究一直是振动与噪声控制领域的研究热点之一。高效精准地预测耦合系统的结构和声场响应有着十分重要的意义,不但可以为结构件的设计优化提供依据,而且对系统采取的减振降噪措施具有指导性作用。
结构声振耦合系统的数值模拟包括结构、声场和它们之间的相互作用。Gladwell等[1]最早建立了基于不同场变量如位移或力相关量的声固耦合理论公式,并进行薄板与空气的声振耦合分析。Craggs[2]详细推导了混合变量(结构采用位移变量而声场采用声压变量)声固耦合系统的有限元方程,使有限元法(Finite Element Method,FEM)逐渐成为解决声固耦合问题的重要手段。但因为有限元法[3]是对全域进行离散,所以主要应用于有界声场的声固耦合分析,且由于其矩阵的稀疏性,相比边界元计算内声场效率较高。针对无界声场问题,一般采用边界元法(Boundary Element Method,BEM)[4]进行模拟,它只需要对声场的边界进行离散,并且自动满足无穷远处的Sommerfeld辐射边界条件,在结构声辐射等外声场问题中具有明显的优势。目前,Nastran、LMS Virtual.Lab Acoustics等常用商业软件的结构声场耦合分析主要采用的就是有限元/有限元耦合法(FEM/FEM)[5-7]和有限元/边界元耦合法(FEM/BEM)[8-10]。在满足声学经验法则[11](一个波长范围内至少要有6个线性单元)的前提下,这两种方法在低频的结构声振耦合数值模拟中都能得到很好的结果。但随着频率的升高,色散误差逐渐增大并占据主导地位;其根本原因是有限元法和边界元法形成的系统刚度偏硬,导致计算的声音传播速度比实际声速快,从而给数值计算带来较大误差。通过减小单元尺寸可以在一定程度上抑制色散误差,但同时会带来巨大的计算时间代价。
近年来Liu等[12]提出了基于广义梯度光滑技术的光滑有限元法(Smoothed Finite Element Method,SFEM)和光滑点插值法(Smoothed Point Interpolation Method,SPIM)[13]。理论证明及大量的数值算例说明光滑方法能够有效地软化系统刚度,从而提高结构和声场的计算精度。姚凌云等[14]将二维光滑有限元应用到声固耦合分析的结构域中,提出了光滑有限元/有限元耦合法(SFEM/FEM),得到了比FEM/FEM更高的精度,但没有对声学单元进行光滑处理。何智成等[15]构建了三维边光滑有限元(Edge-Based Smoothed Tetrahedron Finite Element Method,ES-T-FEM)来计算结构声振耦合中的流体域,结合二维边基光滑有限元(Edge-based Smoothed-FEM,ESFEM)的Mindlin板单元进行耦合分析,其计算精度甚至超过了改进的六面体单元。为了得到无限接近连续系统的刚度,Li等[16]还通过混合光滑有限元方法(HS(Hybrid Smoothed)FEM)(点基光滑有限元(NS(Node-based Smoothed)FEM)与线性有限元的结合)来分别逼近结构和声场的系统刚度,并进行结构声场响应分析,得到的结果与参考解非常吻合。但是,ESFEM和NSFEM都需要重新构造光滑域来进行梯度光滑处理。
本文将Liu等[17]提出的混合单元基光滑点插值法(CSαPIM)应用于声场的数值模拟,结合边基光滑有限元(ESFEM)的板单元[18],对系统进行结构声振耦合分析。与ESFEM和HSFEM相比,由于基于单元的光滑点插值法(Cell-based Smoothed Point Interpolation Method,CSPIM)的光滑域和背景单元重合,因此在形成混合单元基光滑点插值法(CSαPIM)时不需要在背景网格的基础上生成局部光滑域,计算形状函数时只需要在径向基函数形函数基础上以一定权重加上线性有限元对应节点的形函数即可。而且,由于线性有限元采用线性插值方式,在边界面上的3个节点形函数为一定值1/3,使得计算过程更加方便高效。在此声固耦合系统中,结构采用二维三角形板网格,声场采用三维四面体网格,可以很好地适应任意复杂几何模型,减少前处理的工作量。同时,由于计算精度的提高,尤其是针对较高频率的色散误差具有明显的抑制作用,在相同尺寸的网格下,可计算的频率范围更宽,具有极大的工程实用意义。
1 构造基于ESFEM的Mindlin板单元
板结构在汽车、船舶和飞机等交通工具的舱室中应用广泛,研究板结构与声场的耦合作用具有十分重要的工程意义。此处采用二维的三角形Mindlin板单元来模拟结构域,无阻尼板结构振动的离散方程可写为
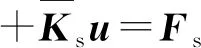
(1)

(2)
(3)
(4)
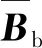
为了消除Mindlin板单元的剪切自锁现象,这里引入离散剪切间隙法(Discrete Shear Gap,DSG)[19]来处理单元的剪切刚度,从而提高计算精度。在应用DSG的板单元中,弯曲应变εb和剪切应变εs可分别写为
εb=Bbue;εs=Bsue
(5)
式中:ue为单元位移向量;Bb和Bs分别为单元的弯曲应变矩阵和剪切应变矩阵。
边光滑有限元已被大量数值算例[20]证明刚度与连续系统非常接近,相比有限元,在同一网格下能够更加准确地模拟结构动力学问题。边光滑指的是构造基于边的光滑域并对其进行应变光滑操作,具体过程如下。
首先利用商业软件自动生成三角形网格作为背景网格,如图1所示。基于三角形的每条边构造光滑域:若边在计算域的内部,则由该边的两端点和共享该边的两个单元的形心点作为顶点形成光滑域;若边在问题域的边界,则由该边的两端点和其所在单元的形心点作为顶点形成光滑域。

图1 基于三角形网格以边为中心的光滑域Fig.1 Edge-based smoothing domain based on triangular meshes
在形成线性有限元的单元应变矩阵的基础上,对光滑域进行应变光滑操作,表达式为
(6)

(7)

(8)

(9)
2 构造基于CSαPIM的声学单元
在理想流体介质和小振幅声波的假设下,无损耗声波方程的离散形式可以描述为
(10)

(11)
(12)

(13)

2.1 浓缩的RPIM形函数
本文将声场域离散成四面体网格,采用混合单元基光滑点插值法(CSαPIM)来进行数值模拟,并通过调整权重参数α∈[0,1]得到与连续系统非常接近的刚度,从而提高声学计算的精度。下面介绍刚度偏软的引入虚拟节点的单元基光滑点插值法(CSRPIM-T5-Cd)的光滑应变构造过程。
在单元基光滑点插值法(CSPIM)中,采用的是基于面的选点模式:对声场域边界上的面采用面的3个顶点(T3形式)进行线性插值,而对声场域内部的面采用面的3个顶点加上共享该面的两个单元的另外两个顶点作为插值点(T5形式),如图2所示。

图2 基于面的选点模式Fig.2 Face-based schemes for selecting support nodes
为避免采用多项式基PIM引起的奇异性问题,本文采用径向基函数(Radial Basis Function,RBF)作为插值形式,它的另一个好处是插值精度高,同时方便支持点的灵活选取。另外,为了满足径向基(Radial Point Interpolation Method,RPIM)的线性再生性,一般会添加一次完全多项式基以改善其性能,确保RPIM能通过标准分片试验。添加PIM(Point Interpolation Method)的RPIM插值形式可表示为

(14)
式中:Ri和ai分别为径向基及其系数;Pj和bj分别为多项式基及其系数;n为局部域的支持点数目;m为多项式基数目,此处取线性完全多项式,即m=4。他们的向量形式可以表示为
aT={a1,a2,…,an};bT={b1,b2,…,bm}
(15)
(16)
(17)
这里选择复合二次形式(MQ-RBF)作为径向基函数,形状参数αc,q采用书中的推荐值。
(18)
式中:ri为支持点i和被插值点的径向距离;dc为问题域内节点的平均间距。使式(14)满足计算点x周围的n个节点值,可以得到n个线性方程,即
(k=1,2,…,n)
(19)
矩阵形式可表示为
ds=RQa+Pmb
(20)
式中:ds为函数值向量;RQ和Pm分别为径向式和多项式的力矩矩阵。
由于式(20)中有n+m个变量,需添加下面m个约束条件作为附加方程方可求解。
(21)
联立式(20)和式(21),最后可以得到对应于n个节点位移向量的RPIM形函数可表示为
(22)
在T5形式的基础上,引入6个虚拟节点,其位置分别取在T5单元6个面的形心上,如图3所示。坐标值可通过下式求得
(23)

通过5个真实节点(1~5)和6个虚拟节点(6~11),共11个支持点进行插值,我们可以得到浓缩前的RPIM形函数
(24)
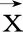
(25)
为了消去虚拟节点的位移,我们假定虚拟节点的位移与所在面的3个顶点位移具有线性关系,即
(26)
将式(26)代入式(25),可以得到
(27)
式中:浓缩后的RPIM形函数可为如下形式
(28)

图3 引入虚拟节点的T5选点模式Fig.3 T5 scheme with virtual nodes for selecting support nodes
2.2 混合单元基光滑点插值法
混合单元基光滑点插值法是指在形成局部域形函数时将刚度偏软的CSRPIM-T5-Cd和刚度偏硬的FEM以一定权数相加并保证权数之和为1,通过改变权数的值来调节离散系统的刚度。当α取合适值时,不但收敛性和计算精度能得到有效提高,而且在畸变网格下也能得到合理的结果。同时,由于单元基光滑点插值方法的光滑域和背景网格重合,所以不需要构造光滑域的步骤,可以节省前处理时间。应用广义梯度光滑技术,我们把原来的梯度替换为光滑梯度,并通过格林公式将域积分转变为边界积分,可描述为以下形式

(29)

(30)

由于FEM相当于单元基光滑点插值法的一种特殊形式,表现为在光滑域的面上采用线性插值形式,也就是说,它在3个顶点上的形函数为一定值1/3,因此不需要额外的计算,只需要在CSRPIM-T5-Cd积分求和得到形函数后直接以不同权重相加即可,如下
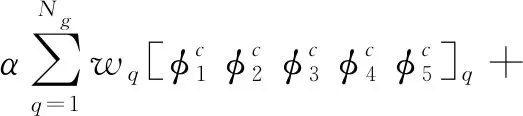
(31)
式中:α∈[0,1]为权重参数;Ng为CSRPIM-T5-Cd的边界面积分选择的高斯积分点数目;wq代表第q个积分点的权数。
最后生成每个光滑域的局部刚度矩阵,并组装成总刚度阵
(32)
(33)
3 结构-声场耦合方程


图4 结构-声场耦合模型示意图Fig.4 Sketch of structural-acoustic coupling model
(34)

根据式(13)可以得到,结构在耦合界面∂Ωsa对声场的作用载荷为


(35)
式中:Na和Ns分别为声场和结构的形函数,这里用的都是线性三角形的形函数;T为将广义位移向量转变为线位移向量的转换矩阵。
(36)
根据式(4)可以得到,声场在耦合界面∂Ωsa对结构的作用载荷为
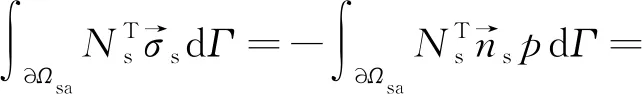
(37)
联立式(1)、式(10)、式(35)、式(37),可以得到时域下无阻尼结构-声场耦合系统的控制方程
(38)
式中:H为耦合矩阵,表达式为
(39)
假设位移和声压均为简谐波函数,则基于频域的结构和声场耦合的强迫响应可以表示为
(40)
4 确定α的取值
本节利用一个具有解析解的声学问题来确定α的取值,通过调节α的值来改变离散系统的刚度,达到接近连续系统的刚度,以提高声学计算的精度。问题域如图5所示,长度为1 m,宽和高均为0.1 m,左边界施加简谐速度激励,右边为完全吸声边界。域中介质为空气,密度ρ为1.225 kg/m3,声速c为340 m/s。精确解的表达式为
p=ρcvncos(kx)-jρcvnsin(kx)
v=vncos(kx)-jvnsin(kx)
(41)

图5 问题域示意图Fig.5 Schematic of problem domain
根据声学经验法则,想要得到可信赖的计算结果,一个波长范围内至少要包括6个线性单元,即波数k和单元尺寸h应满足kh=1的关系。本文在保证kh=1的基础上,选取尺寸分别为0.1 m,0.05 m,0.025 m(对应频率分别为541 Hz,1 082 Hz,2 164 Hz)的三套网格对上述问题进行数值模拟。不同网格全局误差随α变化的曲线,如图6所示。
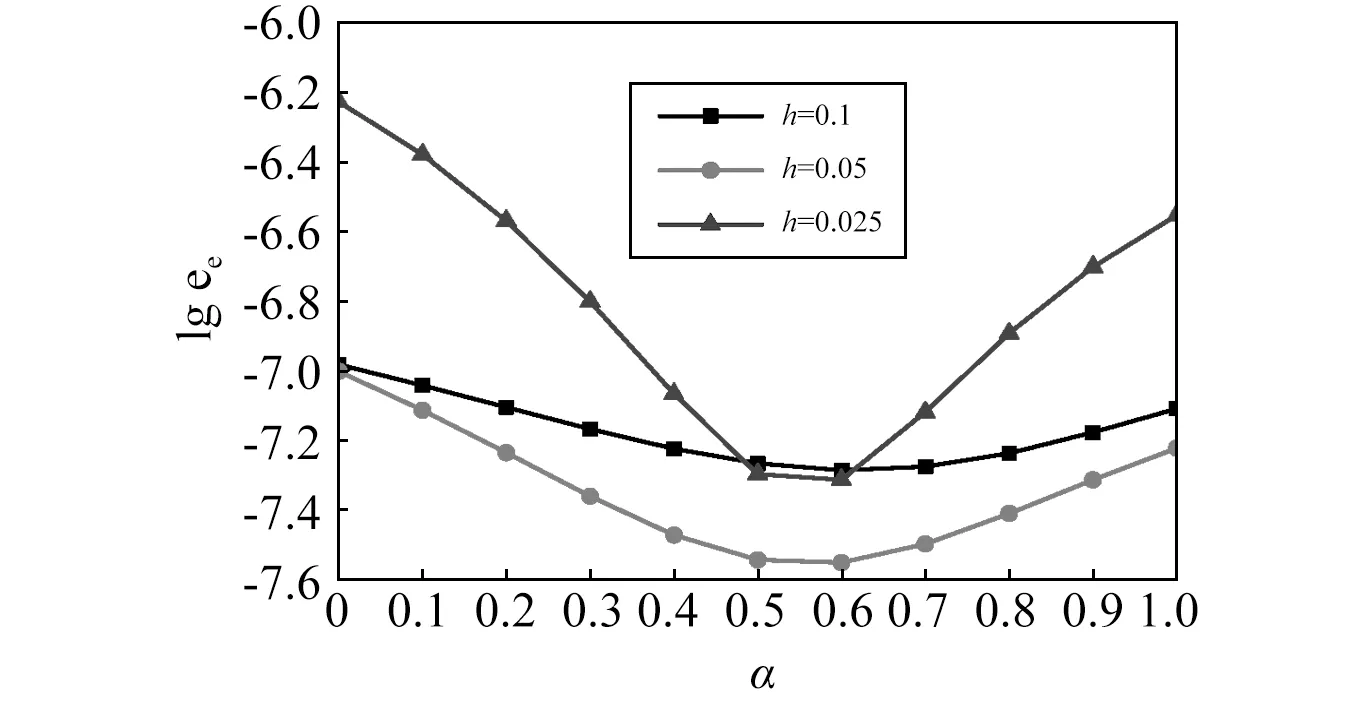
图6 不同α值下的全局误差Fig.6 Global error varying with different α values
其中,全局误差可定义为
(42)
从图6可知,在保证kh为常数的前提下,网格尺寸越细,对应计算频率越高;前者在固定频率下会提高计算精度,后者在固定网格尺寸情况下由于色散误差会降低精度。而当网格较粗时,因为内部单元面较少,形成CSαPIM的形函数所占比例少,所以全局误差变化不明显。但值得注意的是,针对所研究的三种网格形式,当α∈[0.5,0.6]时计算精度一致较高,尤其当α=0.6时,全局误差最小。因此,在下文的声振耦合数值模拟中,基于CSαPIM的声学单元统一取α=0.6进行计算。
5 数值算例
5.1 特征值预测
图7为二维柔性板与三维声场的耦合模型,其中声场域尺寸为0.6 m×0.5 m×0.4 m,上表面为与板的耦合面,其他表面为刚性壁面;板的四边为简支边界,尺寸为0.6 m×0.5 m。声场媒质为空气,密度ρa=1.225 kg/m3,声速c=340 m/s。板的材料为铝,参数如下:弹性模量E=71 GPa,密度ρs=2 700 kg/m3,泊松比ν=0.3,厚度t=0.005 m。

图7 柔性板与声腔耦合模型Fig.7 Flexible plate coupled with acoustic cavity
结构声振耦合系统的计算精度不仅和声场的计算方法有关,还和结构的计算方法有关。本节分别采用FEM/FEM耦合法,FEM/CSαPIM耦合法和ESFEM/CSαPIM耦合法对上述耦合模型进行模态分析。首先把板结构和声场分别离散成三角形和四面体网格,网格尺寸为0.05 m(结构域共148个节点,声场域共1 003个节点),并将不同方法得到的前20阶耦合频率列于表1中,与参考解进行比较。由于该问题没有解析解,这里采用极其细密的等参元模型(单元尺寸为0.01 m,结构域共3 111个节点,声场域共127 551个节点)提供参考解。为了更好地比较计算方法的优劣性,表2列出了参考解模型计算得到的结构与声场的前10阶固有频率。

表1 柔性板与声腔耦合系统的前20阶耦合频率Tab.1 The former 20th eigenfrequencies of coupled systems with flexible plate and cavity
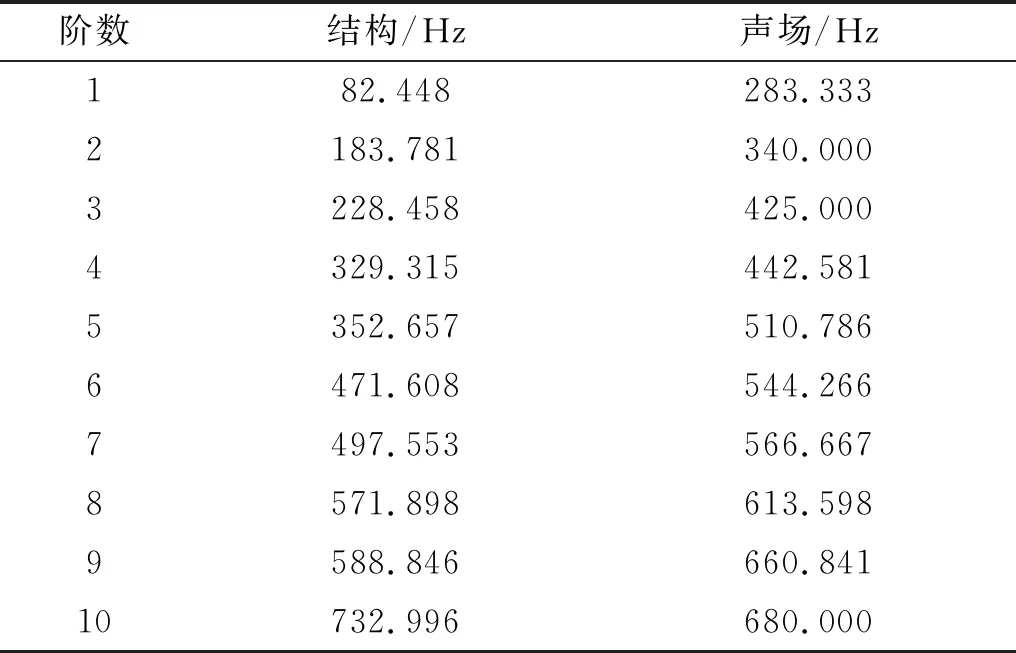
表2 结构与声场各自的前10阶固有频率Tab.2 The former 10th eigenfrequencies of structure and acoustic domain
从表1和表2的结果,我们可以发现:
(1)FEM/FEM耦合法得到的特征频率均比参考值高,这是由有限元过硬的刚度造成的;
(2)FEM/CSαPIM耦合法计算的特征频率相比FEM/FEM耦合法明显更接近于参考值,说明CSαPIM可以很好地模拟声场的刚度,进而提高计算精度。其中,有几阶固有频率的计算值相比FEM/FEM没有较大改善(包括第7阶、第10阶和第11阶、第15阶和第16阶),是因为这几阶频率与结构固有频率较接近,声场固有频率的参与比例较低,而此耦合法只改变了声场的计算方法。同理,精度有明显提高的耦合频率计算值与声场固有频率较接近(例如第9阶、第13阶和第18阶)。
(3)ESFEM/CSαPIM耦合法对特征值的计算精度在3种方法中最高,在特征频率阶次较高时优势更为突出。除了第16阶频率,其他的特征值误差均小于1%。这是因为它不仅能更好地模拟声场刚度,还能得到更合适的结构刚度。
5.2 结构声场响应分析
频率响应分析时振动噪声模拟中必不可少的一环。为了进一步评价CSαPIM与ESFEM结合进行声固耦合分析的效果,本节分别用FEM/FEM和ESFEM/CSαPIM耦合法对耦合系统的频率响应进行数值模拟,在图7所示板的中心点施加幅值为1 N的简谐激励,方向沿z轴。
图8和图9分别绘制了结构节点1(板的中心点,坐标为[300,200,400])的位移响应曲线和声场节点2(某棱边的中点,坐标为[0,0,200])的声压响应曲线,频率范围为0~800 Hz,间隔为2 Hz。为了验证ESFEM/CSαPIM耦合法的鲁棒性,图中同时给出了其在规则网格和畸变网格下的计算结果,网格划分细节如图10所示。参考解同样用5.1所描述的等参元模型获得。结果表明,在0~200 Hz内,两种方法都能得到很好的响应结果;随着激励频率的增大,ESFEM/CSαPIM耦合法计算所得的结果相比FEM/FEM耦合法与参考解更加吻合,无论是结构和声场的响应峰值,还是峰值所对应的频率,都与参考解非常接近。这说明新方法由于准确地模拟了系统刚度,可以大大提高声固耦合响应的计算精度。也就是说,在采用相同网格尺寸的基础上,ESFEM/CSαPIM耦合法的可计算频率范围比FEM/FEM耦合法更广,计算精度可以明显提高。另外,虽然ESFEM/CSαPIM耦合法在畸变网格下的计算结果比规则网格的结果差,但仍优于FEM/FEM耦合法,说明了ESFEM/CSαPIM耦合法的鲁棒性好。

图8 结构节点1的频率响应曲线Fig.8 Frequency response curves of structure node 1
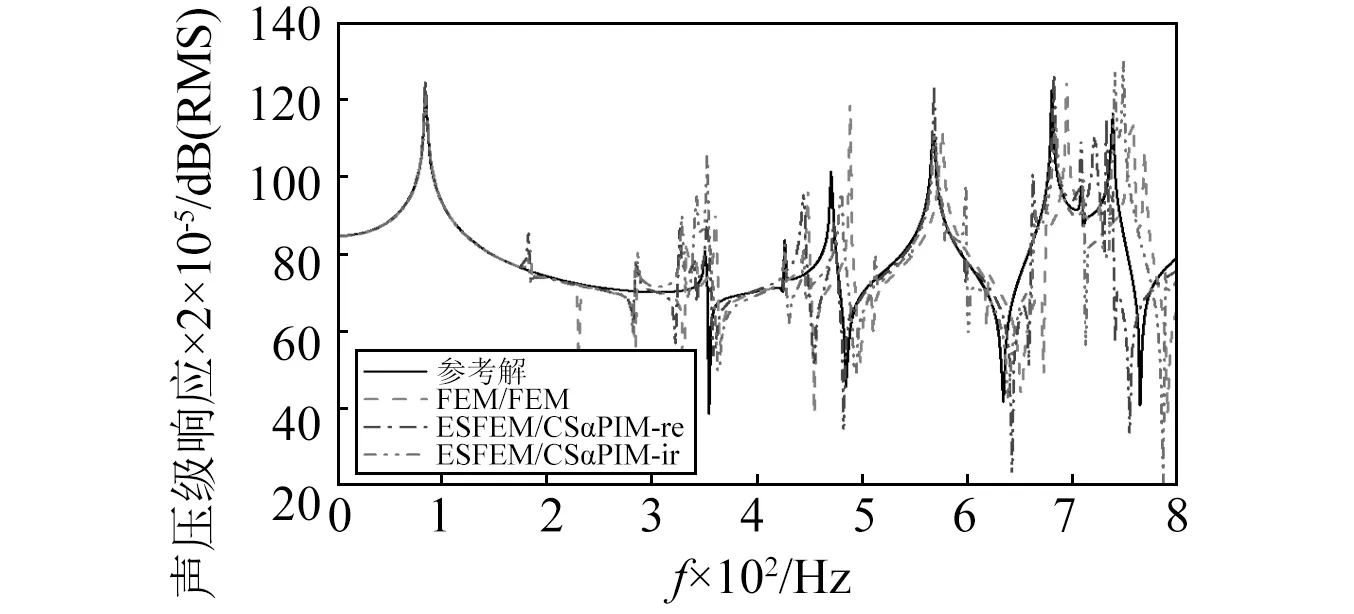
图9 声场节点2的频率响应曲线Fig.9 Frequency response curves of acoustic node 2

图10 网格划分细节Fig.10 Details of the meshes
6 结 论
本文将CSαPIM应用于三维声学计算中,通过基本算例确定合适的α值,并与基于ESFEM的二维Mindlin板单元结合,对声固耦合系统进行特征频率预测和频率响应分析,得到如下的结论:
(1)当α取经验值0.6时,CSαPIM能获得与连续系统非常接近的刚度,明显提高声学计算的精度。
(2)与FEM/FEM耦合法相比,ESFEM/CSαPIM耦合法在相同的网格尺寸下,计算得到的模态特征值更接近参考解,而且频率响应的可计算范围得到有效扩展,可以通过较低的网格要求达到相同的计算精度。
(3)ESFEM/CSαPIM耦合法分别采用三角形单元和四面体单元离散结构域和声场域,可以适应各种复杂几何模型,减少前处理时间,鲁棒性好,具有良好的工程应用前景。
