基于多源信号融合的球磨机负荷预测方法研究

罗小燕，邵 凡，陈慧明，卢小江

(江西理工大学 机电工程学院,江西 赣州 341000)

球磨机是工业生产中物料粉碎的核心设备，其粉碎过程是通过钢球和物料之间的频繁碰撞来实现的。为保证球磨机高效、安全地运作，必须对球磨机内部工作状态进行检测[1]。目前磨机负荷预测的常用方法是利用各种间接检测技术，比如把球磨机的振动、磨音、电流、电压、进出口压差、进出口风温度等为参考量，作为预测磨机负荷参数变化的相关变量，并依此建立磨机内部负荷的软测量方法，应用到球磨机优化控制生产中，以实现整个生产过程工艺参数的最优化[2]。但是在实际生产过程中，基于以上单一因素的球磨机负荷预测存在其局限性，由于矿石性质的波动、外界因素的干扰和操作水平的差异等，球磨机的内部参数难以维持在最佳水平，不能充分发挥球磨机的功效[3]。因此，本文提出一种多源信号融合软测量方法，主要是对球磨机产生的振动、磨音、电机电流信号进行特征提取，获得与磨机负荷参数变化强相关、强稳定性的特征信息，再通过多源信息融合算法步骤建立软测量模型，预测球磨机的内部负荷参数变化。

1 基于支持向量机的球磨机负荷识别

在使用D-S证据理论对磨机负荷进行异类信号融合之前，需要获得辨识框架内各焦元的基本信度函数(mass函数)，它反映了原始信息源或专家知识的经验(统称为证据)对各命题的支持程度。为了解决传统支持向量机(Suppot Vector Mackine,SVM)建模过程中，根据经验对SVM网络的参数惩罚因子C和和核函数参数g的选取问题，本文采用网格搜索与交叉验证相结合的SVM磨机负荷预测方法[4]，该方法基于MATLAB与VC混合编程，建立仿真平台，对SVM参数进行优化，提高相似样本的检索精度和检索效率，具有较好的磨机负荷预测性能。

首先构建训练数据样本和验证数据样本：根据磨机内钢球质量与矿料质量，分别提取欠负荷、正常负荷、过负荷三种不同磨机负荷的多源特征信息，提取每组实验前30 s的多源特征信息值作为SVM训练样本，其余时间段的多源特征信息值可作为验证样本；

利用网格搜索与交叉验证相结合的支持向量机，构造多分类支持向量机对磨机负荷状态进行模式识别；借助MATLAB编程对SVM网络的参数惩罚因子C和和核函数参数g进行优化网络训练，其主要程序为

[bestCVaccuracy,bestc,bestg]=gaSVMcgForRegress(Label,Data)

式中：Label为训练集的标签，分别用1，2，3表示磨机负荷分类的三种状态；Data为输入的多源特征信息值训练样本。

根据多分类支持向量机的输出结果，采用投票法来判断磨机负荷的类型，在辨识框架Θ={α1,α2,…,αn}，将每类票总数和总票数作比就可获得各类磨机负荷的概率，即基本信度分配函数(mass函数)。

2 基于D-S证据理论球磨机多源信号融合方法

2.1 基于D-S证据理论球磨机负荷特征层的数据融合模型

根据D-S证据理论建立球磨机负荷特征层的数据融合模型，其中磨机负荷的分类就是命题，而振动、磨音、电流传感器分别获得信息构成对磨机负荷识别的证据；利用这些证据构造相应的概率分配函数，对所有的磨机负荷赋予一个可信度；概率分配函数以及相应的鉴别框架合称为一个证据体。具体步骤如下：

步骤1将所有磨机负荷的集合分类成非空集合Θ={α1,α2,…,αn}表示，Θ称为基本辨识框架，其中的诸基本问题假设选取依赖于先验知识及认知水平。

步骤2在辨识框架Θ上定义基本信度分配函数(mass函数)m∶2Θ→[0,1]，满足

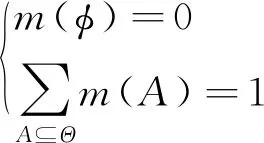
(1)

式中：m(A)为对命题A的信任程度，它反映了原始信息源或专家知识的经验(统称为证据)对命题A的支持程度。如果A为Θ的子集，且m(A)>0，则称A为焦元证据，所有焦元的集合称为证据核。

步骤32Θ上的信任函数Bel和似真函数Pl两个信任测度函数

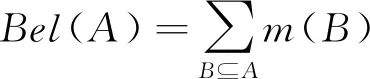
(2)

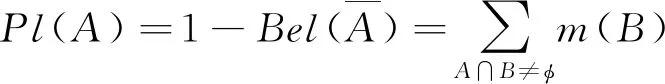
(3)

式中：Bel(A)为支持命题A的信任度;Pl(A)为不否定命题A的信任度，且Bel(A)≤Pl(A)，可将信度区间[0,1]分为3个区间：[0,Bel(A)],[Bel(A),Pl(A)]和[Pl(A),1]。

步骤4设有两个证据e1和e2，它们之间是相互独立的，设e1和e2的基本可信度分配函数分别为m1和m2。对于e1和e2合成的命题A*，e1和e2的基本可信度的D-S合成规则为

(4)

将式(4)归一化处理后得到

(5)

式中:k∈[0,1]为证据e1和e2的全局冲突信度；k越大则说明冲突越大。

从式(5)可知，在经典D-S证据合成规则中，将冲突系数k按运算后的焦元信任值成比例的重新分配给各焦元。但是当k=1，即证据高冲突时，D-S合成规则失效。

2.2 证据冲突的解决方案

针对证据冲突问题的解决方案可以分为两类：①对证据源进行修改；②对证据理论组合规则进行修改[5]。由于球磨机特征信息的样本数据庞大，且在磨矿过程中磨矿因素的耦合变化，导致不同时间段采集的信号可能会存在突变和高冲突信息。因此，通过分析各种融合算法的优、劣点后，采用一种改进的证据合成算法应用于磨机负荷预测中[6]。

首先定义证据ei和ej之间的冲突因子为

(6)

再定义证据ei和ej之间的一致性系数为

(7)

在证据ei和ej之间的一致性系数与冲突因子是一对相反的概念，分别刻画了证据ei和ej之间的一致性信息和冲突信息，为了便于量化处理证据间这种一致和冲突的关系，再引入证据相关度的概念。综合式(6)和式(7)，定义证据ei和ej的相关度为

(8)

由证据相关度rij定义可知，其刻画的是证据ei和ej之间的关联程度，相关度越高，则证据关联程度越高，证据间的冲突也越低；反之，则说明证据关联程度越低，相互支持度越小，证据间的冲突越大。则在磨机负荷预测中，提取ΔT=(Δt1+Δt2+…+Δtm)时刻内的信号特征，得到的m条证据相关度矩阵Rij

(9)

相关度矩阵Rij的任意i行之和越大，则说明证据ei被其它证据所信任，证据ei在融合系统中的信誉度越高，证据可靠；反之，则说明证据ei的信誉度低，证据可靠度低。

用证据全局信誉度μ(ei)描述任意证据ei在融合系统中全局信誉度，全局信誉度最高的证据称为融合系统的权重证据，再以权重证据为依据，计算每条证据的权重系数τi，其表达式为

(10)

证据融合：根据式(1)～式(10)计算m条证据的权重系数，并对每条证据的基本信度分配函数(mass函数)进行重新分配，得到新的基本信度分配函数为

(11)

由此可得将式(5)的合成规则改进为新的D-S证据合成公式为

(12)

综合以上公式可知，针对不同时间段采集的信号可能会存在突变和高冲突信息的问题，改进后的D-S证据融合方法充分挖掘磨机负荷特征信息间的一致性和冲突性；在证据权重分配时，最大限度的降低了可靠性低的证据对融合结果的影响；最后得到改进后的D-S证据合成公式可应用于高冲突信息的融合计算。

3 磨机负荷预测的实例验证与结果分析

3.1 磨矿实验

实验采用江西某矿山的钨矿石、φ330×330 mm Bond指数球磨机，其电机功率为0.75 kW,碎磨前对矿石物料进行初级破碎，并对矿石进行筛分。将加球量、给料量、入料粒度分布、球配比作为实验输入参数；以排料量(-200目产率)、能耗作为输出参数[7]；为获取磨机在磨矿过程中的振动、磨音、电流信号，分别将DH131振动传感器布置在轴承座上，MA231声音传感器经固定装置布置在离球磨机30～50 cm处，DV105电流表接在电机上。采集球磨机轴承振动、筒体磨音、主电机电流信号，作为检测磨机负荷的外部响应变量,东华DH5922N动态数据采集仪对球磨机的振动、磨音、电流等各种物理量进行测试和分析。

为获取不同负荷下的特征信息，分别以填充率10%(欠负荷)、填充率20%～40%(正常负荷)、填充率50%(过负荷)三种磨机负荷状态，以料球比为0.6、粒级配比为1∶2∶2∶2∶3的矿物入料粒度、1∶3∶4的钢球直径配比进行磨矿实验，筛分并记录相关的实验数据。分别对振动、磨音、电流信号进行特征提取，得到不同时间段内的信号特征信息值；根据支持向量机训练方法，对特征信息进行基本概率分配，形成初始的证据源，再应用改进后的D-S证据合成规则，得到磨机负荷预测结果，根据该结果得到相应的磨机负荷调控措施，确保球磨机稳定在最佳工况下运行。

3.2 融合算法的对比分析

为了验证改进后的D-S证据合成规则的有效性，应用磨矿后的数据进行实例验算。设定磨机负荷的辨识框架为Θ={A,B,C}={欠负荷，正常负荷，过负荷}，对振动信号进行频域分解，采用小波包3层分解，选取2～8 kHz频率段，以各个频率段能量值和总能量值作为频域特征信息值，由图1可知，振动信号的总能量值、5～8 kHz能量值变化较大，不具有稳定性；而2～5 kHz各频段的能量值变化较小具有稳定性，可作为正常负荷时的频域特征信息值。磨音信号经短时傅里叶变换且把幅度转变为声压级，图2可知，在前30 s不同时间段，磨音信号的0.8 kHz，1 kHz，1.6 kHz，2 kHz频带的A计权1/3倍频程声压级值变化较大，不具有稳定性；而A计权总声压级值和1.25 kHz，2.5 kHz频带的A计权1/3倍频程声压级值变化较小，具有稳定性，可以作为正常负荷时的磨音信号特征信息值。

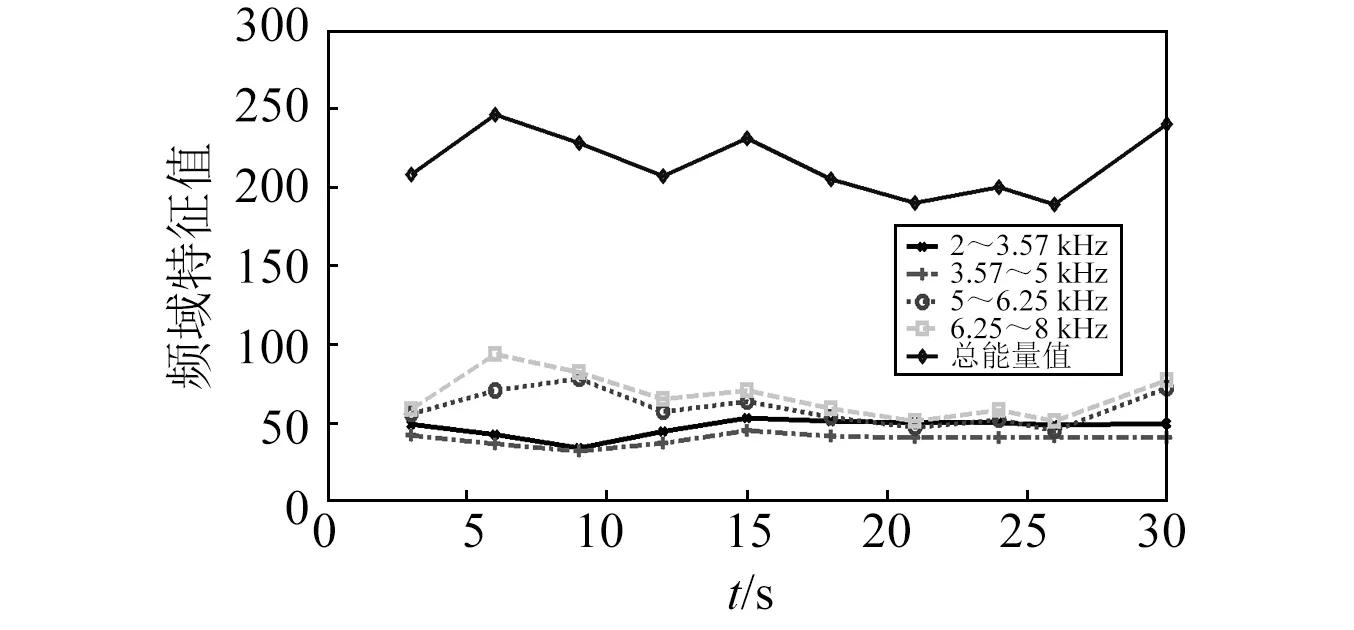
图1 振动信号频域特征信息Fig.1 Vibration signal frequency domain feature information

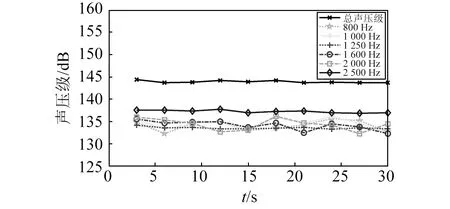
图2 不同时间下磨音信号声压级的变化Fig.2 Changes of sound pressure level of grinding signal under different time

根据多源信号特征提取的结果，采集5条带有高冲突特征信息值的实验数据作为证据，如表1所示。

由网格搜索与交叉验证的支持向量机算法和专家先验知识，得到上述5条证据的基本概率分配函数赋值，如表2所示。

在表2中数据可知，证据e2指向欠负荷，而其余4条证据均指向正常负荷，属于高冲突证据。根据文献[8-10]的证据融合算法及本文方法式(12)，分别对此5条证据进行逐次合成，得到的融合结果如表3所示。

表1 磨机负荷的特征信息值Tab.1 Characteristic information of the mill load

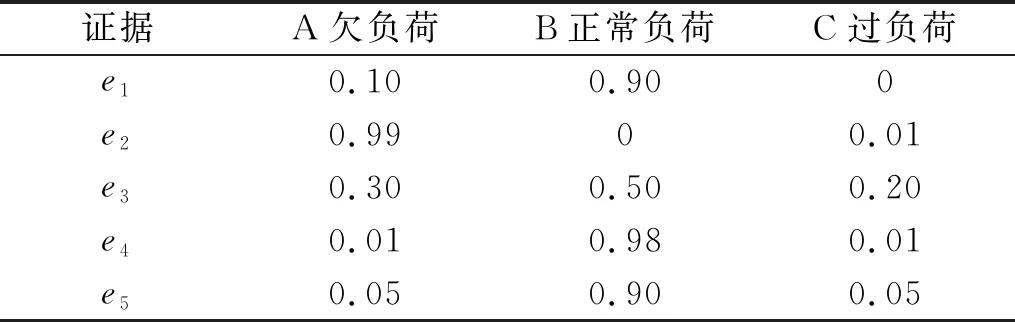
表2 证据的基本概率分布Tab.2 Basic probability distribution of evidence

表3中：Θ为指全集；m(Θ)为不确定的概率。由融合结果可知，随着证据数量增加：孙全方法融合结果由m(B)=0.234增加到m(B)=0.378，邓勇方法融合结果由m(B)=0.165增加到m(B)=0.403，两者在处理冲突证据时都显得过于保守，不利于根据融合结果作出实时决策；而Murphy方法融合结果由m(B)=0增加到m(B)=0.8，虽对冲突证据有一定的融合效果，但效率偏低；经典D-S合成规则无法融合高冲突证据，得到与事实不符的融合结果；而本文方法对B正常负荷的预测结果由m(B)=0.405增加到m(B)=0.816，说明随着证据量的增加，预测结果准确性越来越高，不仅融合效率高，而且融合结果收敛速度也快。

表3 融合结果比较Tab.3 Comparison of fusion results

3.3 预测准确性的对比分析

为了进一步验证本文融合方法在磨机负荷预测中的可行性和准确性，再进行以下实验验证：在进行磨矿实验中，每组实验都采集了5 min的多源信号，选取每组实验前30 s的多源信号数据作为训练样本，建立磨机负荷的特征信息数据库；再选取第60～90 s的信号用于实验验证与对比分析。

将磨机负荷的识别框架分类为Θ={A,B,C}={欠负荷，正常负荷，过负荷}，提取每组实验前30 s的多源信号，每间隔Δt=3 s的信号进行信号处理，提取磨机负荷的特征信息值作为先验信息数据库；采用相同方法，对每组实验第60～90 s的多源信息进行信号处理，得到相应的多源特征信息值作为预测磨机负荷的证据，应用改进后的最优融合集算法，排除强突变、高冲突的证据；根据已建立的先验信息数据库，通过支持向量机算法和专家先验知识，得到每条证据的基本概率分配函数赋值，再应用改进的D-S证据融合规则，计算每条证据的融合权重系数，进一步排除强突变、高冲突的证据，重新分配剩余证据的基本概率赋值，对每条证据逐条融合，得到所有验证数据最终的融合结果。

利用相同的实验数据，分别应用孙全等、邓勇等和Murphy的证据融合算法对证据进行逐次合成，将预测结果与实际分类结果相对比，得到不同融合算法的融合结果对比图，如图3所示。

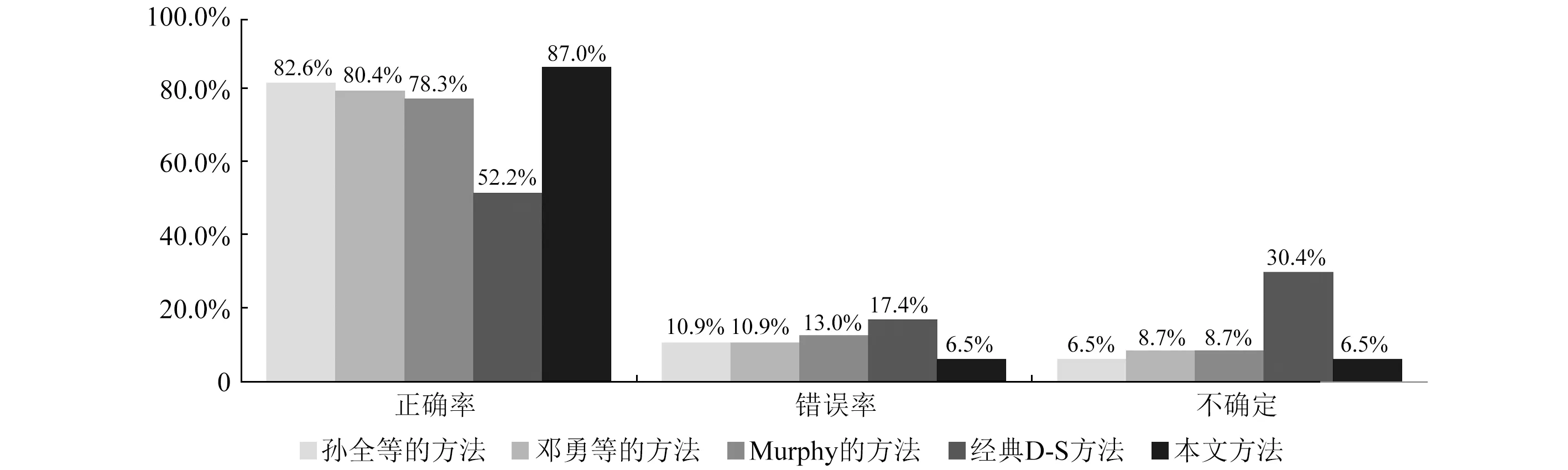
图3 不同融合方法的融合结果对比Fig.3 Comparison of fusion results for different fusion methods

由图3可知，本文的融合方法所预测的正确率最高，错误率和不确定性最低：磨机负荷预测准确率达到87%，表明本文方法在对磨机负荷预测和状态识别中却实可行，具有较高的准确性。

孙全等的方法通过引入证据可信度，对冲突性证据按照加权和平均的形式进行分配，但是证据可信度的主观性比较大，计算结果之间的差异会比较明显，导致最终的融合结果不一致；邓勇等和Murphy的方法都是对单个证据先进行了多次合成，再从证据源中提取特征信息，应用组合后得到的平均信息进行证据融合，导致一些证据信息丢失，也不利于融合决策的应用；经典D-S方法不利于合成高冲突的证据，其错误率和不确定性都比较高。与上述方法相比，本文改进的证据合成算法优点是综合考虑了证据间的一致性信息和冲突信息，根据相关度矩阵的计算结果来对每条证据的mass函数进行重新分配，最大限度的降低了可靠性低的证据对融合结果的影响，有利于提高预测结果的准确性。

4 结 论

针对单因素的球磨机负荷预测方法存在的局限性问题，本文采用多源异类信号的特征级融合方法，运用SVM训练方法对特征信息进行基本概率分配形成初始证据源。针对经典D-S证据融合方法存在突变和高冲突信息的问题，提出一种改进后的D-S证据融合规则。采用改进后的D-S证据融合规则对磨机负荷进行特征级融合，得到球磨机负荷预测结果，并通过实例验证和对比分析，表明该方法最大限度的降低了可靠性低的证据对融合结果的影响，融合效率更高，收敛速度更快，提高预测结果的准确性。根据该结果得到相应的球磨机负荷调控措施，能够确保球磨机稳定在最佳工况下良好运行。