复杂背景下对称差分解析能量算子在轴承故障诊断中的应用

徐元博，蔡宗琰，丁 凯

(长安大学 道路施工技术与装备教育部重点实验室，西安 710064)

微弱信号检测已经在众多科研领域得到了广泛应用，因此逐渐成为一种新兴的技术手段。微弱信号的检测有两个较为显著的特点：①在较低的信噪比下检测到有用的信号；②要求检测的速度要尽量快、具有时效性，使其能最大限度的满足工况现场实时监测和故障诊断的要求[1]。轴承故障信号极其容易被噪声覆盖或被其他振动频率干扰，如转子不平衡，转子不对中和齿轮啮合等。因此，轴承故障信号也属于微弱信号的一种，所以在对轴承的故障进行诊断时，所采用的检测技术也要尽量满足上述的两个特点。由于频谱分析可以快速分辨出信号的频率结构以及各谐波幅值、相位、功率及能量与频率的关系，因此在轴承故障特征提取领域得到了广泛应用。频谱分析包括幅值谱，倒频谱，功率谱，细化普，希尔伯特解调和能量算子等方法。由于机械设备故障信号，尤其是轴承故障信号会产生周期性的脉冲冲击力，产生振动信号的调制现象而形成调幅或调频信号，因此在这些频谱分析方法中，基于解调技术的希尔伯特解调(Hilbert Transform，HT)和能量算子解调(Teager Energy Operator，TEO)技术更多的得到了学者们的青睐。相比于HT，TEO用于分析和跟踪窄带信号的能量，具有解调精度高、响应速度快等优点，不仅可以用于窄带单个调幅、调频信号的解调，还可与用于宽带的多个调幅、调频信号组合的解调，对于对比分析不同类型信号具有重要意义[2-4]。但是传统的TEO也有着较为明显的缺点，其一就是在解调精度过低，能量谱中容易出现负值；其二就是对噪声和振动干扰非常敏感[5]。为了改进传统TEO的上述不足，一种基于中心有限差分方法(Central-Finite Difference)的对称差分能量算子(Energy Operator of Symmetrical Differencing，EO_SD)被提出，并在提取轴承故障特征方面得到了较好应用。尽管EO_SD完全克服了TEO的第一个不足，但在第二个缺点上，EO_SD虽然进行了改进，但是当背景环境更为复杂，仍然会受到较大影响。因此从文献[6-9]中可知，故障信号在某些环境下仍然需要进行必要的前处理后，譬如滤波处理或模态分解，才能用EO_SD进行解调。但一般的滤波处理都需要设置参数，而模态分解算法相对比较耗时，因此将该种故障提取方法应用于现场的实时监测有时较为困难。因此，本文在EO_SD的基础上提出对称差分解析能量算子(Analytic Energy Operator of Symmetrical Differencing，AEO_SD)，该方法不仅很好的保留了EO_SD的优点，不需要前处理以及设置参数，并且在面对更为复杂的工况环境时，具有更好的鲁棒性，能从严重污染的信号中快速准确提取出轴承故障特征。

1 AEO_SD原理

传统的TEO最早由Teager提出，主要用来研究语音信号。他将该能量算子定义如下

(1)

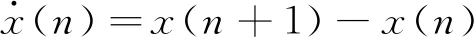
ψ[x(n)]=x2(n)-x(n-1)x(n+1)

(2)

但是利用前向差分求导后，得到的真实值与理论值的最大误差可达11%，造成解调精度不高的后果[10]。因此EO_SD采用了中心有限差分方法(Central-Finite Difference)代替前向差分即

(3)

该差分序列可以对原离散信号进行平滑处理，从而提高解调的精确度。同时可以看出该差分序列的采样点为对称分布，因此也称对称差分。

根据解析信号理论，一个信号的解析形式都可通过幅值解调和瞬时频率来表现一个信号的特征。因此在对称差分的基础上引入解析信号的概念。

首先，定义解析能量算子如下[11]

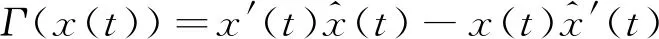
(4)

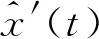
式(4)的离散形式可以由式(5)表示

(5)

采用了中心有限差分方法代替前向差分，将式(3)代入式(5)得到对称差分解析能量算子，如式(6)所示

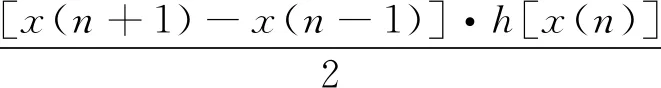
(6)

2 仿真实验

2.1 解调精度对比实验

为了验证AEO_SD的解调精度，采用下式的模拟信号与EO_SD和TEO进行对比，

x(n)=1.3 cos(nπ/8)+3.1 cos(nπ/32)

(7)

信号时域图和能量谱图如图1和图2所示，从图2中的虚线可以明显看出，采用前向差分方法的TEO的能量谱出现了负值，而使用对称差分的AEO_SD和EO_SD在其能量谱中没有出现负值，说明这两种算法的解调精度都得到了提高。

图1 时域Fig.1 Time domain

图2 能量谱Fig.2 Energy spectrum

2.2 轴承模拟故障信号实验

为了证明AEO_SD具有更好的鲁棒性，本小节采用一组模拟轴承故障信号进行验证，并且与HT,TEO和EO_SD进行对比体现其优越性，该模拟信号如式(8)所示

(8)

式中：位移常数y0=5；阻尼系数ξ=1；冲击故障周期Tp=0.009 5 s，即故障频率fg=104.86 Hz；固有频率fn=3 000 Hz，ωn=2πfn。首先，在式(8)中加入SNR=-5 dB的强背景噪声，观察四种算法仅在噪声存在情况下的性能。图3表示冲击信号，图4为加上背景噪声的混合信号。

图3 冲击信号Fig.3 Impact signal

图4 混合信号Fig.4 Mixed-signal

现分别使用四种算法对混合信号进行故障特征提取，四种算法的包络谱和能量谱如图5(a)～图5(d)所示。从图5可知，除了TEO没有把模拟故障特征频率提取出来外，其他三种算法都可以将故障特征频率提取出来。对于HT算法，能在较强的背景噪声下成功的提取出故障特征频率，是因为通过信号的解析形式固有的调幅和调频能力都具有一定的降噪能力[12]。而对于EO_SD如前文所述，改用中心有限差分后，对数据进行平滑处理，起到了抑制噪声的作用。虽然这两种算法可以较好的提取出故障特征频率，但还是可以从图5(d)看出，在同等量级下(0～0.6)，AEO_SD所提取出的故障频率以及它的倍频的峰值远远大于HT和EO_SD的，因此可以看出AEO_SD的性能优于其他三种算法。

为了在更为复杂的环境下体现AEO_SD的优越性，在加入背景噪声的基础上再加入四组频率分别为33 Hz，43 Hz，50 Hz和310 Hz的干扰频率，使其信号受到更加严重的污染，该信号的时域如图6所示。

图5 性能对比Fig.5 Comparison of performances

图6 重度污染信号Fig.6 Heavily contaminated signal

仍然使用上述四种算法对该重度污染信号进行故障特征频率提取，提取效果如图7(a)～图7(d)所示。严重污染的信号通过四个算法进行处理后，可以发现，与图6(b)结果一样，TEO仍然是失败的。而HT和EO_SD在更为复杂背景下也失去了提取故障特征频率的能力，从他们的谱图中只能看到干扰频率以及他们的组合频率(频率相加或相减)，如图中黑方框中所示。因此这两种方法也是失败的。但从图7(d)可知，虽然干扰频率以及他们的组合频率也存在于AEO_SD的能量谱中，但这并没有影响它的故障特征频率的提取能力，故障特征频率及其它的倍频在图中清晰可见。

图7 性能对比Fig.7 Comparison of performances

同时，为了更好体现AEO_SD在运行速率上的优势，本小节采用引言中提到的基于模态分解的提取方法与之进行对比，本次采用的模态分解算法为变分模态分解算法(Variational Mode Decomposition,VMD)[13]，该方法已经在很多文献中被证明为性能最好的模态分解算法[14-16]。

现用VMD将重度污染的信号进行分解，分解后的各个子信号的波形图,如图8所示。

剔除前三个振动干扰频率，选取上图中BLIMF4为轴承故障子信号，分别使用HT，TEO和EO_SD对其进行处理，得到的结果如图9所示。

图8 子信号的波形图Fig.8 Waveform of sub-signals

图9 基于VMD的故障提取方法对比Fig.9 Comparison of performances of the VMD-based methods

从图9可知，正如引言中所说，经过VMD的前处理，去除掉振动干扰频率和部分噪声后，HT，TEO和EO_SD均能提取出轴承故障特征频率，这也是大多数文献中采用的方法。虽然该方法可以较好的提取出故障特征频率，但不可忽略的一点是这种联合方法耗时是非常巨大的。图10为上述三种方法与AEO_SD运行时间对比图，采样点数从1 000～10 000点，分解个数K=5，运行条件均采用配置为酷睿i5双核，内存4 G的台式电脑，运行软件为MATLAB2017a@。

图10 时间对比Fig.10 Comparison of runtime

从图10可知，三种基于VMD的提取方法在运行时间上并无太大差别，运行时间随着采样点数的增加也随之增加，当采样点为10 000时，可以看到运行时间已经将近达到约12 s。相比于上述三种方法，AEO_SD的运行时间非常少，并且随着数据的增大，时间的变化也非常小。

因此，通过上述对比实验可知，虽然经过前处理后的HT，TEO和EO_SD同AEO_SD一样，可以在复杂的背景环境下提取出故障特征频率，但AEO_SD的运行效率相比之下非常高，更有可能应用于实际工况当中。

3 真实轴承故障数据实验

为了验证AEO_SD在实际现场下的实用性和普遍性，本次实验将该算法分别应用到旋转机械轴承故障诊断和振动机械轴承故障实验上。

3.1 旋转机械轴承故障诊断

本次实验中，采用美国西储大学在公共网络平台上提供的轴承故障数据，该轴承相关频率参数如表1所示。

表1 轴承相关频率Tab.1 Associated frequency

图11为轴承外圈的时域和频域图，从频域图上可以看到轴承的故障特征已经被噪声淹没。

图11 外圈故障信号Fig.11 Outer faulty signal

现使用上述四种方法对其故障特征频率进行提取，如图12(a)～图12(d)所示，从图12可知，与模拟实验中加入较强的背景噪声不同，在实验室工作条件下。由于旋转机械运行时背景噪声相对较小而且此次实验中没有其他干扰频率影响，可以看到四种方法均能较好的提取出轴承外圈的故障特征频率。但跟模拟实验一样的是，虽然这几种方法都可以提取出故障特征频率，但AEO_SD能量谱中的故障频率以及它的倍频的峰值都明显高于其他三种方法的。因此，旋转机械轴承故障诊断实验也同样表明AEO_SD优于其他三种算法。

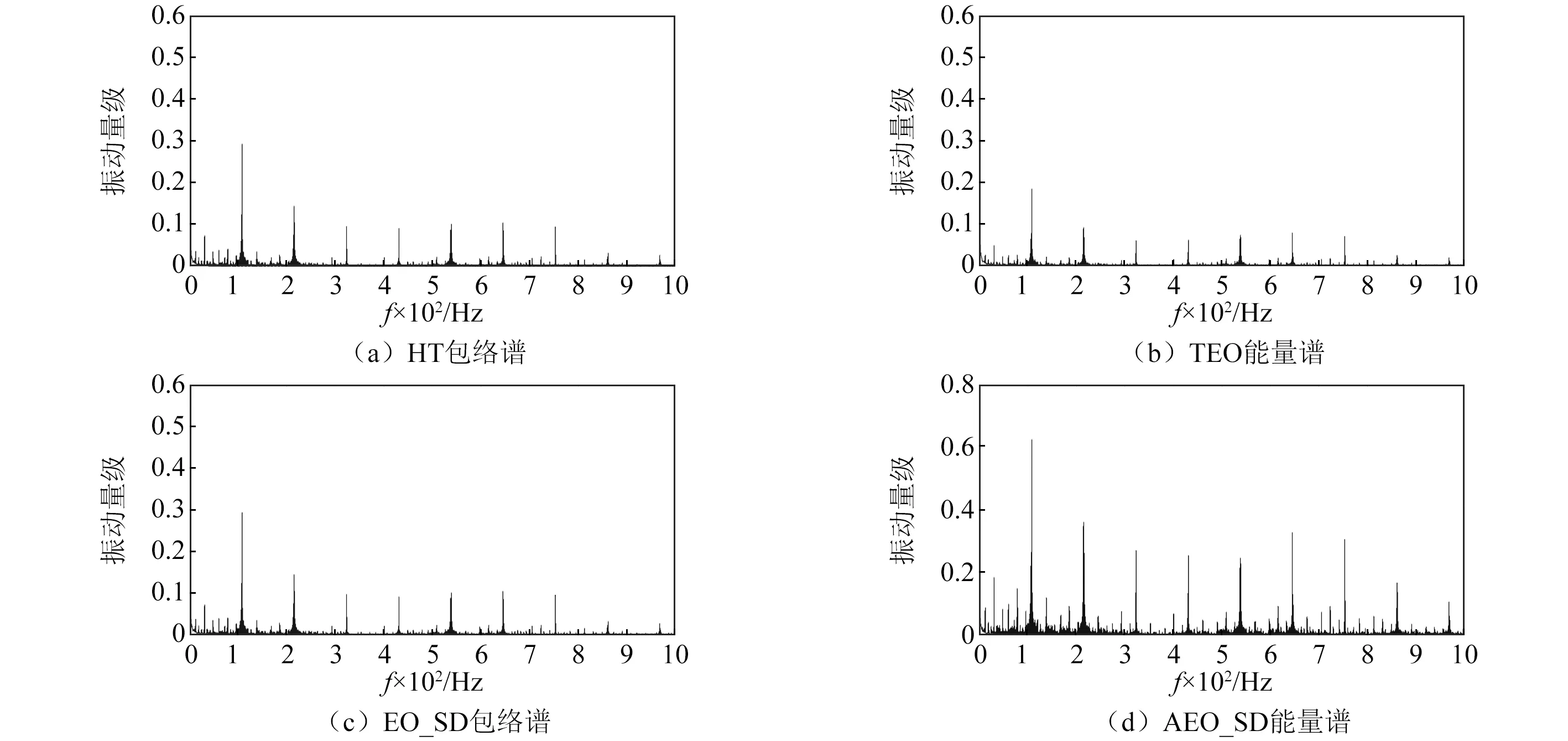
图12 性能对比Fig.12 Comparison of performances

3.2 振动机械轴承故障诊断

一般来说，振动机械相较于旋转机械，由于结构特点不同，因此运行原理和信号特点也不尽相同，其主要有背景噪声异常强大，其他干扰频率普遍存在等特点[17]。因此，振动机械的轴承故障特征提取难度要大于旋转机械，对其算法的鲁棒性要求更高。本次实验采用的振动机械为振动筛，其实验平台如图13所示，该振动筛的偏心块可以进行更换产生不同的振动量级，从而产生不同强度的背景噪声和振动频率干扰。

1-筛箱；2-电机；3-偏心块；4-选择轴图13 数据采集系统和振动筛Fig.13 Dataacquisitionsystem and vibrating screen

该振动筛轴承型号为1 308调心球轴承，相关尺寸信息如表2所示。外环故障尺寸为1 mm×0.2 mm(宽×深)，内环的故障尺寸为0.7 mm×0.2 mm(宽×深)，其示意图如图14所示。

表2 轴承相关尺寸Tab.2 Parameters of the bearing

图14 轴承内圈和外圈损伤尺寸示意图Fig.14 Diagram of the inner race and outer race of the damaged bearings

根据轴承理论故障频率计算公式

(9)

(10)

式中：fo为外圈故障特征频率；fi为内圈故障特征频率；Nb为滚动体数量；f为旋转频率；Bd为滚动体直径；Pd为节径；θ为接触角。计算得出的轴承内外圈故障如表3所示。

表3 轴承相关频率Tab.3 Associated frequency

为了检验AEO_SD算法在真实数据下的最好性能，本次实验选用质量最大的偏心块，使其振动筛在运行过程中产生最大的背景噪声和转子不平衡现象，从而得到严重污染的轴承故障信号。

首先进行内圈的故障特征频率提取，它的时域和频域图如图15所示。可以看到振动筛轴承故障的时域信号与旋转机械的时域信号有着较大不同，它的信号运动趋势不再是一条直线而是类似于正弦曲线，这就是由于偏心块的存在造成了转子不平衡现象，从而信号受到影响[18]。

图15 内圈故障信号Fig.15 Inner faulty signal

使用上述四种方法对振动筛轴承故障信号进行处理，包络谱与能量谱如图16(a)～图16(d)所示。可以明显看到经过四种方法处理后得到的包络谱和能量谱结果跟旋转机械有着很大的不同，随着背景噪声的增大和其他频率的干扰，在旋转机械轴承故障诊断中表现较好的HT，TEO和EO_SD，它们的轴承故障特征频率提取能力都大幅度下降。尤其是TEO已经不能将故障特征频率提取出来。虽然HT和EO_SD能勉强检测到轴承故障特征频率，但在谱图上可以看到，轴承特征频率及其它的倍频的幅值非常低并且伴随着干扰频率或它们的组合频率。而对于AEO_SD，虽然它的故障特征频率检测效果也相对下降，但还是可以在谱图中明显看出其轴承内圈故障特征频率及其它的倍频。

图16 性能对比Fig.16 Comparison of performances

对外圈的故障特征频率进行提取，外圈的故障信号时域图和频域图,如图17所示。从图17可知，外圈的故障信号特征与内圈是一致的。

同内圈一样，现使用上述三种算法与AEO_AD对外圈的故障特征频率进行提取，提取的结果如图18所示。从图18可知，同内圈的提取情况相类似，虽然HT和EO_SD能检测到轴承故障特征频率，但在谱图上可以看到，轴承特征频率及其它的倍频的幅值较低，在EO_SD的能量谱中仍然可以看到峰值较高的不平衡故障频率特征。而TEO无法提取出外圈故障特征频率。相对于上述三种算法，可以看到AEO_SD的提取效果非常明显，它的故障频率特征及其倍频都可以非常清楚在包络谱中辨认。

图17 外圈故障信号Fig.17 Outer faulty signal

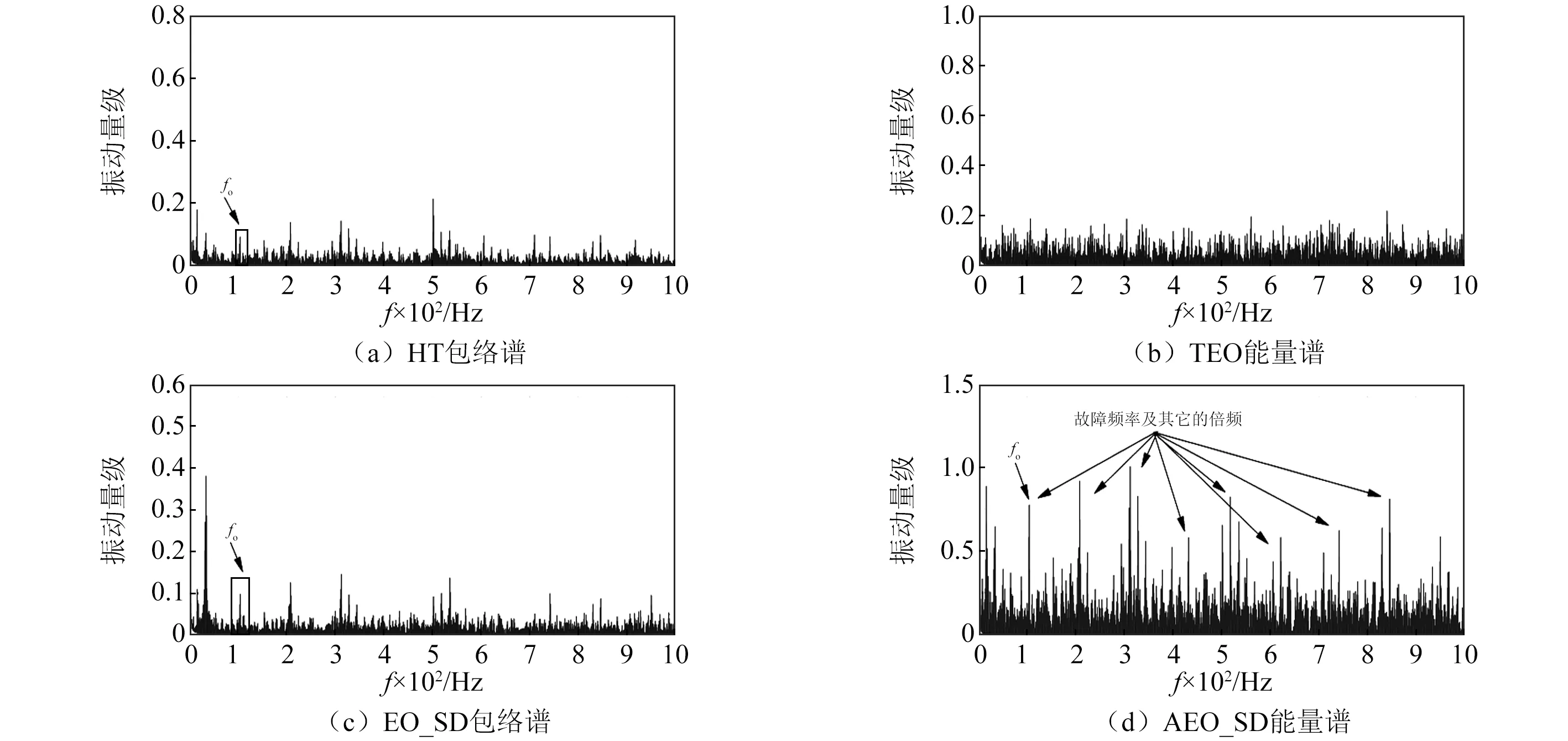
图18 性能对比Fig.18 Comparison of performances

4 结 论

针对先前常用的HT，TEO和EO_SD等解调算法的不足，提出了一种可替代的能量算子方法—对称差分解析能量算子。该方法原理简单易懂，并且在使用前无需前处理和参数设置。通过模拟仿真实验和真实轴承故障诊断实验，验证了该算法具有更好的解调能力与出色的运行效率，尤其是在复杂的背景环境下。因此将该解调方法用于复杂背景下的轴承或齿轮故障诊断领域是可行的。

从验证实验可知，该方法可以从严重污染的信号中提取出故障特征频率，但从图7(d)中还可知，在干扰频率较多的情况下，该方法还是不能完全抑制干扰频率，干扰频率仍然可以从能量谱中清晰可见。这个不足也是日后需要改进的地方。