基于分形理论的结合面法向接触刚度模型
2019-06-13陈虹旭董冠华殷国富
陈虹旭,董冠华,殷 勤,谭 峰,殷国富
(四川大学 制造科学与工程学院,成都 610000)
动态特性是制约高端机床发展的重要因素,目前对机床动态特性的研究主要采用实验和有限元相结合的方法[1]。研究表明,机床结合面提供了机床60%~80%的柔度特性,如何对结合面准确的建模是建立机床有限元模型的关键问题[2]。
目前结合面法向接触刚度模型大多基于M-B分形理论,该理论认为微凸体变形前的顶端曲率半径R是一个随微凸体变形量δ变化的值[3-6],这导致对变形量δ求导时不能把曲率半径R视为常数[7]。然而,从微凸体变形前的顶端曲率半径的实际含义出发,该参数应仅受微凸体尺度的影响,不应该与微凸体的接触变形量有关。之所以出现该矛盾,是因为M-B模型在推导过程中忽略了微凸体的压缩过程。Morag等[8]对该问题提出了一个修正的分形理论,遗憾的是在他们在推导过程中存在错误,同时也未能给出最终的力学表达式。
本文基于修正的分形理论模型,推导出了结合面法向接触刚度模型。该模型考虑了微凸体的接触变形过程,解释了微凸体变形前的顶端曲率半径R与接触变形量的关系。基于该模型,计算出了结合面法向接触刚度值并录入有限元模型进行仿真,进而与实验结果进行对比。对比结果表明,仿真结果与实验结果基本一致,该模型可有效的进行结合面法向接触刚度值计算。
1 粗糙表面接触模型
1.1 W-M函数
对于具有连续、自仿射、不可微的分形特征的表面轮廓,可用W-M函数描述[9]
(1)
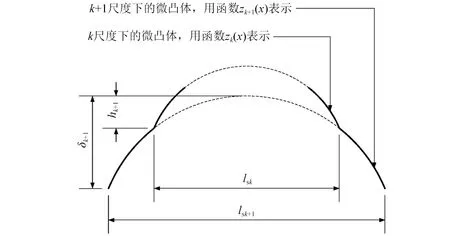
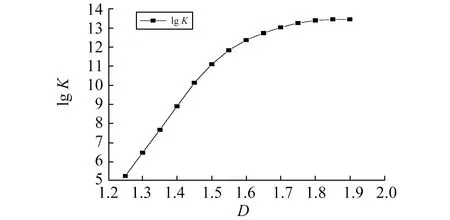
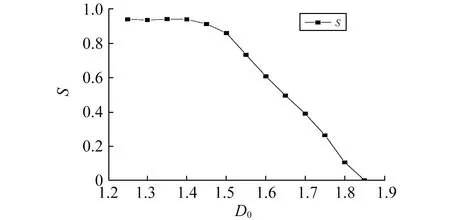
式中:z(x)为粗糙表面轮廓的高度;D为粗糙表面轮廓的分形维度,1 W-M函数由无数个余弦函数组成,设截止长度为lts=γ-(nh+1),nh为与最高频率γnh对应的系数,波长小于lts的分形细节将被忽略。 如图1所示,用k(k=0,1,2,…,nh)定义与刚性平面接触的微凸体的尺度,则该尺度下的微凸体名义接触长度ltk(lsk-1 (2) 式中:int[…]为向下取整;ltk为k尺度下的微凸体名义接触长度,lsk-1 (3) 微凸体变形前的顶端曲率半径可由式(4)求得 (4) 微凸体高度为δk=GD-1(γk-nh)2-D,微凸体的接近量wk为 (5) 图1 k尺度下的微凸体Fig.1 Asperity of scale k 该模型将k尺度下的微凸体高度δk和微凸体接触变形量wk进行区分,微凸体变形前的顶端曲率半径不再是接触变形量的函数。 第k尺度临界接触变形量可表达为[10] (6) 当wk (7) (8) 在弹性变形区(ke≤k≤nh-nl)内,用刚性平面所在的那一尺度微凸体进行受力计算。由于接触变形是刚性平面从较小尺度微凸体压缩至较大尺度微凸体的一个连续过程,如图2所示。该过程不同于赫兹接触过程中的单个微凸体变形。为了使第k尺度微凸体和第k+1尺度微凸体在两尺度交界位置的计算值相等,进行如下分析计算 图2 误差补偿示意图Fig.2 Error compensation (9) 式中:hk+1为刚性平面进入k+1尺度时第k+1尺度的预压缩量。 为便于计算,代入常用值γ=1.5(同理也可做一般性推论),则有 (10) 根据赫兹接触理论[11],两尺度交界处受力的差值为 pkm-pk+1h=pkm·Δ (11) 式中:pkm为第k尺度微凸体处于最大压缩量时的受力;pk+1h为第k+1尺度微凸体压缩量为hk+1时的受力;Δ为一个常数,可由式(12)求得 (12) 由式(11)可知,弹性变形从某一尺度进入后一尺度时,用该模型计算会丢失一部分力。考虑通过误差补偿进行修正,若k0尺度的受力远小于所关心的尺度k0+t(t=1,2,3,…),从k0尺度开始修正,有 (13) 由式(13)可求得k0+t尺度修正后的弹力为 pk0+1m·Δt-1+pk0m·Δt (14) 考虑到0.204 5<Δ<0.469 7,近似有 (15) (16) 式中:pk0+th为k0+t(t=1,2,3,…)尺度修正前微凸体压缩量为hk0+t时的受力。 (17) (18) (19) 因此,式(17)还可写为 (20) 采用M-B模型中的面积分布函数[12-14],假设面积大于a′的接触点总数为N,N满足 (21) (22) (23) 粗糙表面塑性变形总载荷 (24) 式中:Pp为粗糙表面的塑性变形总载荷。粗糙表面处于弹性变形区(ke≤k≤nh-nl)第k尺度的微凸体受力 (25) 粗糙表面弹性变形总载荷为 (26) (27) (28) 粗糙表面总载荷为 P=Pp+Pe (29) 根据球体间赫兹接触推导得出的弹性接触的面积公式,单个微凸体发生弹性变形的真实接触面积为 (30) 采用和式(26)相似过程对式(30)积分,可得结合面弹性变形的真实接触面积为 (31) 式中:f3,f4分别由式(32)、式(33)求得 (32) (33) 式(17)两端对接触变形量wk求导,可得单个微凸体的法向接触刚度为 (34) 考虑整个名义面积内所有微凸体的接触刚度,采用和式(26)相似过程对式(34)进行积分,可得结合面的法向接触刚度表达式为 (35) 式中:f5,f6分别由式(36)、式(37)求得 (36) (37) 实验结合面材料为45号钢,表面经磨削加工,弹性模量为210 GPa,表面硬度为300 MPa,采用M8×35的螺栓连接,各螺栓连接力矩为20 N·m,其示意图如图3所示。 图3 结合面示意图Fig.3 Sketch of joint surface 加工过程中,使用一块300 mm长的毛坯进行磨削加工,之后采用线切割切下10 mm长的表面制作检测样品,保证样品和结合面的一致性。采用布鲁克原子力显微镜对样品表面情况进行检测,检测结果如图4所示。 图4 表面检测结果Fig.4 Surface test results 采用结构函数法提取其分形参数,结构函数可写为 S(τ)=CG2(D-1)τ(4-2D) (38) 式中:C可由式(39)求出 (39) 在双对数坐标系下,结构函数S(τ)和τ呈直线关系。当斜率kτ满足0 D=(4-kτ)/2 (40) 再由直线在S(τ)轴上的截距可计算出G值。实测轮廓数据为离散值,记采样间隔为Δt,共采样N组数据,则可用nΔt(n=0,1,…)代替τ,离散的结构函数为 (41) 受限于实验设备的测量精度和数据的舍入误差,结构函数并非绝对线性,因此可采用最小二乘法拟合一条直线。将粗糙表面轮廓数据导入Matlab中进行处理,得到结构函数和最小二乘拟合直线,如图5所示。对10 μm×10 μm和20 μm×20 μm检测表面分别取3组轮廓数据,计算各组数据的分形维度和特征尺度参数,并按式(29)、式(35)计算法向接触刚度,计算结果见表1。 图5 结构函数与拟合直线Fig.5 Structure function and fitting line 表1 分形参数及法向接触刚度计算值Tab.1 The calculated values of fractal parameters and normal contact stiffness 为研究螺栓结合面的动力学特性,对比理论建模与实验数据之间的差距,本文开展了基于m+p噪声振动测试系统的模态实验,实验中结合面建模如图6所示。 螺栓结合面采用两柔性绳悬吊,模拟自由边界状态,以移动力锤法对各测点的法向和切向进行激振,在测点1处设置三向传感器进行数据采集。测试范围为3 000 Hz,测得的数据通过以太网上传至计算机,经SO Analyzer后处理,得到结合面前8阶模态。模态判据MAC图如图7所示。可见实验结果中各阶模态已充分解耦,具有很高的置信度。 图6 结合面几何建模Fig.6 Geometric modeling of joint surface 图7 模态判据MAC图Fig.7 Diagram form of modal criterion(MAC) 取表1中10 μm×10 μm检测表面中3组法向接触刚度平均值作为第一组结合面法向接触刚度K1,可得K1=2.27×107N/m;取20 μm×20 μm检测表面中3组法向接触刚度平均值作为第二组结合面法向接触刚度K2,可得K2=7.93×106N/m。 之所以分别计算两组法向接触刚度值,是因为在测量不同尺度的检测表面时,受检测仪器精度的影响,测得的分形维度值存在一定的误差。注意到特征尺度参数处于同一量级,而计算出的法向接触刚度值有较大差异,为探究法向接触刚度与分形维度之间的关系,取结合面法向载荷为50 000 N,特征尺度参数G为5×10-11,D=1.25,1.3,…,1.9。以分形维度D作为横坐标,法向接触刚度的对数lgK作为纵坐标,绘制关系曲线如图8所示。 图8 法向接触刚度和分形维度的关系Fig.8 The relation between normal contact stiffness and fractal dimension 由图8可知,当分形维度D<1.5时,分形维度每提高0.05,法向接触刚度就增加一个数量级,可见在一定范围内分形维度对法向刚度的影响是很大的。当分形维度D>1.5时,随着分形维度的增高,法向接触刚度的变化率逐渐减小。为进一步说明,定义法向接触刚度对分形维度的灵敏度S(后面简称灵敏度S),记 (42) 式中:KD0为分形维度为D0时所求得的法向接触刚度;KD0+ΔD为分形维度为D0+ΔD时所求得的法向接触刚度。 S表征了在分形维度D0附近出现ΔD的变化时,法向刚度计算值对分形维度变化的敏感程度,S越接近于1,计算出的法向接触刚度对分形维度的变化就越敏感。取D0=1.25,1.3,…,1.85,ΔD为0.05,其余参数与图8相同,绘制S与D0的关系如图9所示。 图9 灵敏度S与分形维度D0的关系Fig.9 The relation between sensitivity S and fractal dimension D0 由图9可知,当分形维度小于1.5时,灵敏度S>0.8,随分形维度的增加变化缓慢,法向接触刚度受分形维度变化的影响较大;当分形维度大于1.5时,灵敏度S迅速下降,法向接触刚度受分形维度的影响减小。 结合面切向刚度采用参数识别的方法获取[16],并通过有限元仿真与实验结果的对比来保证其准确性,所得刚度值为Kt=7.5×109N/m。根据所求得的刚度值,基于吉村允孝积分法的思想,在ANSYS中采用COMBIN14单元录入结合面刚度信息,建立有限元仿真模型。仿真结果表明,前8阶理论振型与实验振型一致,限于篇幅仅列出第二组数据固有频率误差最大的第4阶振型对比和误差最小的第6阶振型对比,如图10所示。理论固有频率与实验固有频率对比见表2。 表2 理论固有频率与实验固有频率对比Tab.2 Comparison between theoretical natural frequency and experimental natural frequency 图10 理论振型与实验振型对比Fig.10 Comparison between theoretical modal shapes and experimental modal shapes 由表2可知,固有频率计算值均小于实验值,说明所求得的法向刚度值偏小。其中第4阶为结合面法向二阶弯曲,误差最大,第6阶为结合面切向一阶弯曲,误差最小。所求得的法向刚度值偏小的原因是因为该模型在计算受力时考虑了塑性变形,而在计算刚度时忽略了塑性变形和弹塑性变形的影响,因此计算出的刚度值是偏小的。 (1)建立了结合面法向接触刚度模型并进行了实验验证,结果表明理论模型和实验模型前8阶模态的振型一致,固有频率的误差为-10.2 %~-1%,间接论证了模型的正确性。 (2)本文模型在计算受力时考虑了塑性变形,而在计算刚度时忽略了塑性变形和弹塑性变形的影响,因此计算出的结合面法向接触刚度值是偏小的。 (3)当分形维度小于1.5时,法向接触刚度对分形维度的灵敏度S>0.8且变化缓慢,法向接触刚度受分形维度的影响较大;当分形维度大于1.5时,灵敏度S随分形维度的增大而快速减小,法向接触刚度受分形维度的影响减小。因此,当结合面的分形维度小于1.5时,提高分形维度可以有效提升结合面的法向接触刚度。1.2 微凸体接触变形模型

1.3 微凸体临界接触变形量


2 结合面法向接触刚度模型
2.1 微凸体弹性变形模型的误差补偿




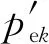

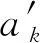
2.2 结合面法向载荷



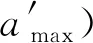
2.3 结合面法向接触刚度




3 法向接触刚度模型实验验证
3.1 分形参数的测定




3.2 模态实验
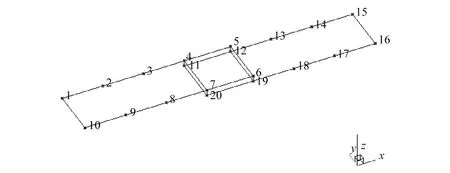

3.3 法向接触刚度与分形维度的关系
3.4 理论模态与实验模态对比


4 结 论
