向量式有限元的力-位移复合控制方法

曲激婷，胡 强，宋全宝

(大连理工大学 建设工程学部工程力学研究所，辽宁 大连 116024)

2004年普渡大学Ting等[1-2]从向量式力学的基本概念出发，提出一种新的数值分析方法—向量式有限元(也称有限质点法)。该方法将结构离散为一群质点，用质点的运动描述结构的行为，同时引入“虚拟逆向运动”和“途径单元”的概念，在不断更新的基础架构上计算单元内力。由于不需要集装刚度矩阵及迭代求解非线性方程，该方法可以有效处理结构大变形、弹塑性等非线性行为；此外，由于在计算过程中可随意增加单元和改变边界条件，在分析结构不连续行为时，与传统的有限元方法相比具有很大优势[3]，目前已在薄膜屈曲褶皱[4]、断裂模拟[5]、桥梁倒塌[6]等多个领域取得了研究成果。

力控制和位移控制是实验中两种常用加载方法，当结构刚度很大时通常采用力控制，当刚度衰减、结构软化时可使用位移控制[7-8]。然而，由于实验花费高、周期长、混合控制加载方式存在困难等原因，使得基于理论分析的数值计算方法成为研究人员进行结构分析的重要手段。目前，绝大部分基于向量式有限元的研究中，同一结构、同一分析过程外加激励(包括荷载和位移)的施加方法主要有两种，即单独使用力控制加载或单独使用位移控制加载，这在一些实际问题中存在一定的局限性。有时，同一实验过程中会先后使用了两种控制加载方法；此外，实际结构的工作状况通常很复杂，在地震作用下建筑或桥梁结构部分构件会产生大变形、大转动甚至断裂，分析构件性能变化或模拟结构破坏过程时，通常采用力控制法在上部结构构件上施加自重等均布荷载，在地震发生过程中将地震加速度时程转化为位移时程施加在结构支座，即同一结构的不同部分需要同时进行力控制加载和位移控制加载。向量式有限元可以实现实验中的混合控制加载方式，程序编写简单方便，改变边界条件灵活。目前关于力-位移混合控制的研究还较少，因此，有必要针对向量式有限元理论进行力-位移复合控制研究，为实验加载装置稳定、安全、方便的实现力与位移混合控制提供理论依据。

本文基于向量式有限元基本原理，提出力-位移交替控制方法和力-位移混合控制的方法(统称为力-位移复合控制方法)；前者考虑两种控制方法在各自适用的阶段独立工作，根据分析过程中结构刚度的变化，“接力”交替采用，即实现力控制和位移控制时间上的组合；后者是在分析过程中部分结构采用力控制，部分结构采用位移控制，实现力控制和位移控制空间上的组合。

1 向量式有限元的基本理论

向量式有限元是结构行为分析的新方法，创新性地提出了点值描述、途径单元和虚拟逆向运动的概念。该方法在空间上将结构离散为一群质点，用质点的运动来描述结构的几何形状和空间位置的变化，质点之间采用无质量的结构单元连接和传递内力，质点的运动满足牛顿第二定律。结构中质点的运动方程[9]可写成

(1)

将式(1)转化为差分形式进行数值求解，即

(2)

式中：d为质点位移；Δt为时间步长；下标n+1，n和n-1分别为第n+1，第n和第n-1时刻的变量。通过式(2)可以在外力已知的情况下求位移，即位移控制加载的方法。

当已知结构运动路径时，可选用位移控制加载法计算作用在节点上的外力[10]，即

(3)

忽略惯性项对变形的影响，则结构的实际变形可以分解为刚体运动和纯变形，内力只与纯变形相关，而与刚体运动无关。因此，在求解单元的内力时，需要从结构的实际变形中扣除刚体运动部分,向量式有限元通过逆向运动来实现这一过程。以一个桁架单元为例(见图1)，t1时刻桁架杆单元位于A1B1位置,t2时刻单元位于A2B2位置。为了求得此过程中杆单元轴力变化量，先将单元从A2B2平移以消除刚体平动的影响，再将单元以A1为参考点，逆向旋转Δθ到A1B4位置以消除刚体转动的影响。

图1 逆向运动Fig.1 Reverse motion

比较A1B1和A1B4的形状,当Δt取值很小时，杆件在此时间段内长度的变化量很小，可采用材料力学公式求出轴力增量Δf。再将Δf与t1时刻的杆件轴力相加，可得变形后的单元轴力为

(4)

式中：ft1，σt1，lt1，et1分别为t1时刻杆单元的轴力、应力、长度和方向向量，ft2和lt2为t2时刻杆单元的轴力和长度。根据静力平衡准则，可求得杆件两端其余内力。再经过正向的刚体平移和Δθ的刚体正向转动,使杆件回到t2时刻位置(见图2)，此时得到的杆件轴力为t2时刻杆件真实的轴力。

图2 正向运动Fig.2 Forward motion

2 力-位移复合控制方法

以力控制方法为例，向量式有限元的分析流程可以概括为以下几个步骤：

步骤1输入各构件的材料、截面性质、阻尼系数、时间步长和总分析时间等参数；

步骤2划分结构的质点和结构单元并分别进行编号；

步骤3根据材料、截面性质和构件尺寸计算质点质量；

步骤4将tn时刻的质点内力、外力、位移、速度初始化为零向量，利用中心差分法计算tn-1时刻质点位置和速度；

步骤5用中心差分法计算出tn+1时刻质点位置；

步骤6令支座处质点的tn+1时刻位置为初始位置；

步骤7遍历所有单元，求单元在[tn,tn+1]时间内的纯变形，计算作用在质点上的内力；

步骤8更新当前分析时刻，读入下一时刻施加在结构上的外力，将步骤5计算的质点位置作为tn时刻质点位置；

步骤9判断当前时刻是否已达到总计算时间，若否，则重复步骤5～步骤8；若是，则进入下一步；

步骤10后处理，输出计算结果。

采用位移控制的分析流程与采用力控制方法相似，仅需在步骤6将指定自由度上的位移指定为当前时刻的位移，在步骤8使用式(3)计算在该自由度上施加的外力，同时将“读入下一时刻施加在结构上的外力”修改为“读入下一时刻施加在结构上的位移”，其余步骤均相同。

力-位移混合控制是指在分析某种复杂工况下结构的内力和变形时，部分结构采用力控制加载，部分结构采用位移控制加载。以图3所示的刚架为例，假定tn时刻该结构在A点外力Pn和B点水平位移Un的共同作用下发生变形，Un是一个按照指定规律变化的位移，Un与Pn互相独立，结构的变形和内力将是这两种外加激励共同作用的结果。

力-位移交替控制是指进行结构分析时部分时段使用力控制，部分时段使用位移控制，但在任一个时段，结构上只存在一种控制方法。这一方法需要解决两个问题：一是两种控制切换的时机；二是两种控制切换的方法。本文对两种控制方法的切换时机采用人为指定的方法确定，采用力控制时，当单位力增量引起的位移大于某一量值时，将力控制切换到位移控制；采用位移控制时，当单位位移增量对应的外力增量大于某一量值时，将位移控制切换为力控制；起始阶段可任意指定一种控制方法。本文侧重讨论两种控制方法在同一分析过程中并存的可行性，因此重点讨论第二个问题—两种控制的切换方法。按照前述的分析流程，对于两种控制的切换采用如下方法：(a)当判定结构需要从力控制切换到位移控制时，在步骤8记录当前时刻的位移x0，并从此刻起不再读入外力增量，从下一时刻的步骤6起，在x0的基础上读入位移增量；(b)当判定结构需要从位移控制切换到力控制时，在步骤8记录当前位移增量对应的外力P0，并从此刻起在P0的基础上读入外力增量；从下一时刻的步骤6起，不再读入位移增量。

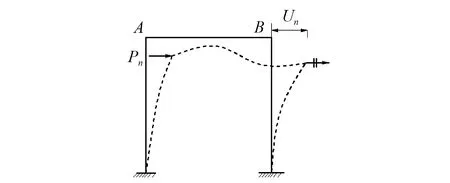
图3 力-位移混合控制Fig.3 Force-displacement mixed control method

3 数值分析

算例1力—位移混合控制

一个由8结点和13个杆件组成的平面桁架[11](见图4)，各杆件截面面积和材料特性相同，截面面积为2.5×10-3m2，弹性模量为2.1×1011N/m2，密度为7.8×103kg/m3。采用基于向量式有限元的力—位移混合控制方法，分析该平面桁架在外力和位移同时作用下的静力大变形。时间步长取Δt=1.0×10-4s，分析时间取0.3 s，阻尼系数μ取100。设D点受竖直向下的集中荷载P=3×107N，同时在B点施加Δ=0.5 m的竖向位移(见图5)。荷载和位移的施加过程如图6所示。

图4 平面桁架Fig.4 A plane truss

图5 外力和位移施加位置Fig.5 Position of external load and displacement

根据“2”和“3”节的内容，采用MATLAB编程，计算结果如图7和8所示，D点竖向位移为向下的0.476 m，B点外加荷载为向上的7.75×106N，同时可以得到AC杆的轴力为1.141 5×107N。为了验证结果的正确性，将D点竖向荷载P=3.0×107N与计算得到的B点竖向荷载7.75×106N同时施加到结构上，采用SAP2000进行考虑大变形的静力非线性分析，可以得到D点竖向位移为向下的0.474 m，AC杆轴力为1.141 5×107N，与采用力-位移混合控制的向量式有限元法计算结果吻合得很好，从而验证了本文提出的力-位移混合控制方法的正确性。

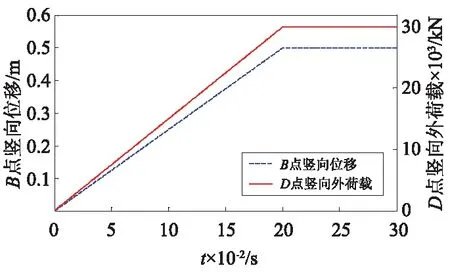
图6 荷载和位移施加过程Fig.6 The applied process of external load and displacement

图7 D点竖向位移Fig.7 Vertical displacement of point D

图8 B点外加荷载Fig.8 External load at point B

算例2力-位移交替控制

采用传统非线性分析中经典算例，一个由24根杆件铰接而成的空间桁架穹顶结构(见图9)，杆件弹性模量为3.03×103N/m2，截面面积为3.17×10-4mm2，密度为6.309×103kg/m3，所有杆件材料特性和截面面积相同。当作用在结构上的荷载达到某一临界值时，结构将发生屈曲。设穹顶A点作用一个集中荷载P，采用向量式有限元方法对该穹顶结构屈曲过程进行分析，时间步长取Δt=5.0×10-4s，阻尼系数μ=300。

图9 空间24杆星型穹顶结构Fig.9 A reticulated space structure composed of 24 members

基于向量式有限元的基本理论建立结构模型，分别采用力控制法和位移控制法对此算例进行分析：力控制时取P=853 N,单位力增量为0.043 N；位移控制时A点竖向位移d=50 mm,单位位移增量为2.5×10-6m。

计算A点的竖向荷载与竖向位移变化情况，得到荷载-位移关系曲线即荷载-位移平衡路径(见图10)。将位移控制时的计算结果与文献[12]中的计算结果进行对比，两者基本吻合，说明向量式有限元能够对穹顶结构的屈曲过程进行追踪，本文方法有效且分析结果正确。

对比图10中力控制方法和位移控制方法的结果可见，两曲线在位移为0～8.5 mm和44.5～50 mm的区段吻合得较好，而在8.5～44.5 mm区段有很大差异。差异产生的原因是由于采用力控制时，A点竖向位移达到8.5 mm后，继续增加力时微小的力增量引起了巨大的位移增量，A点及与其相连杆件突然向下凹陷，即在8.5～44.5 mm区段采用位移控制时，A点不再处于平衡状态，该段不再是星型桁架真实的平衡路径。图11为采用本文方法计算得到的空间桁架穹顶结构在A点竖向位移达到44.5 mm后的形态。此结构的刚度不大，采用位移控制时的增量步长也已取的足够小，仅使用位移控制法就已能够得到完整的荷载-位移关系曲线，采用力控制法追踪荷载-位移平衡路径并无优势。

图10 A点力和位移关系曲线Fig.10 Force-displacement curves at point A

为了说明根据向量式有限元建立的分析模型使用力和位移交替控制的可行性，在A点交替使用力控制法施加外力和位移控制法施加竖向位移以追踪空间桁架穹顶结构的荷载-位移平衡路径。A点位移为0～8.5 mm时使用力控制，当A点竖向位移达到8.5 mm时，将力控制切换成位移控制，在A点竖向位移达到40 mm时，再将位移控制切换回力控制；在此过程中分析程序并未暂停或重启，直到A点竖向位移达到50 mm分析结束，分析结果如图12 所示。两种控制方法切换位置处计算结果发生轻微振荡，但由于阻尼的影响及加载过程中力增量和位移增量均较小，振荡很快消失，荷载-位移关系曲线趋于平稳。为减弱两种控制方法切换位置附近的振荡现象，可以将切换点的时间提前，如果将第一次切换位置由8.50 mm变为5.56 mm，得到荷载-位移关系如图13所示。由图13可知，荷载—位移曲线变得更加光滑，并与文献[13]的结果十分接近。说明对向量式有限元静力分析模型采用力-位移交替控制方法是可行的，且计算结果也较为准确。

图11 空间桁架屈曲Fig.11 Buckling of the space truss

图12 力和位移交替控制的力-位移曲线Fig.12 Force-displacement curve by alternating

图13 切换点在5.56 mm处时的力-位移曲线Fig.13 Force-displacement curve when the force and displacement control method switching point is 5.56 mm

两个数值算例表明：位移加载时可自动通过第一个坡，对应的力自动增减；力加载时位移能够自动增减；两者结合的最终目的是希望结合两种加载方式的优势。

4 结 论

本文根据向量式有限元的基本原理，提出力-位移混合控制和力-位移交替控制方法，通过数值算例的分析，验证了本文提出的力-位移复合控制方法的正确性和可行性，此方法可以实现更加复杂的分析工况，拓展了向量式有限元的应用范围。由于向量式有限元采用物理模式描述结构的行为，各质点运动方程独立求解，无需组集刚度矩阵，无需迭代求解方程，无论是力-位移交替加载，还是力-位移混合加载，都没有给计算带来本质的困难，分析程序步骤清晰、过程简单、通用性强，简单方便的实现了结构发生大转动、大变位时力-位移复合控制方法。

(1)在运用向量式有限元的力-位移交替控制法时，不同的控制模式切换位置对于结果的影响不大；向量式有限元的运用使得力和位移混合控制变得十分便利，在处理存在大变位的结构复杂加载过程时具有一定优势。

(2)对基于向量式有限元的力-位移复合控制仅展开了初步讨论，在此基础上，如果能够选取合适的指标判断两种控制模式切换的时机，就能够自动地、不需要人为干预、不需要特殊处理、且在不需迭代求解非线性方程组的情况下追踪到更加复杂的结构的完整荷载-位移平衡路径。