淹没条件下环境流速对磨料水射流流场特性的影响

杨胜发，黄 岱，曾施雨

(1.重庆交通大学 河海学院，重庆 400074；2.国家内河航道整治工程技术研究中心，重庆 400074；3.长江重庆航运工程勘察设计院，重庆 401147)

在传统清礁工艺中，水下爆破是常用手段，虽技术成熟，工效较高，但对水生生态环境的影响极大。目前，长江上游航道等级提升的各个重点建设项目全部位于包括有国家一级重点保护野生动物白暨豚、江豚、中华鲟在内的国家级自然保护区内。由此可以预见研发一种新型的环保清礁技术，对于未来推动我国内河航运事业的绿色生态发展是极其必要的。故提出了一种磨料水射流清理礁石的技术，高压水射流破岩技术是射流技术应用的一个重要方面，尤其在石油、煤炭工程中更是用于破岩钻井的常用手段[1-4]。这种高速挟砂水射流切割能力强，在切割材料时不会发生任何物理或化学变化，淹没环境下切割时没有机械噪音，取材方便，环保无污染。本文所做研究即是为磨料水射流水下作业提供参考。

1 理论综述

1.1 两相流模型的选取

基于上述两种两相流模型的基本分类思想，目前，对于多相流的处理采用的数值计算方法有两种：欧拉—拉格朗日方程和欧拉—欧拉方程。其中这几类计算模型应用广泛：VOF(Volume of Fluid)模型、欧拉模型、混合物模型、离散相模型(Discrete Phase Model,DPM)[5]。其中前三者模型属于连续介质模型，采用欧拉—欧拉方程计算；离散相模型属于离散颗粒模型，采用欧拉—拉格朗日方程计算。

(1)VOF模型

主要用于跟踪两种或多种不相容流体的界面位置，不同流体组成共用一套动量方程计算。常见运用于自由面流动、液体中气泡的流动、大坝决堤的水流运动、分层流等。

(2)欧拉模型

通过建立一套包含n个动量方程及连续方程的模型来求解每一相，压力项和各界面交换系数是耦合在一起的。常运用于颗粒悬浮、流化床和气泡柱等情况。

(3)混合物模型

一种简化的欧拉模型，各相仍被处理为互相贯穿的连续介质。模型求解的是混合物的动量方程，并且通过相对速度描写离散相。常运用于沉降、气泡流和低负载粒子负载流等。

(4)离散相模型

在拉氏坐标系中模拟固相颗粒，模型首先通过计算连续相流场，然后再求解颗粒相的运动物理量，从而追踪颗粒的运动轨迹。该模型假定在离散相浓度低，分布稀疏的条件下进行模拟计算，一般要求其体积分数小于10%，仅考虑流体对固相颗粒的作用，忽略颗粒之间的相互作用以及颗粒对流体的作用。

1.2 固相的拟流体化

实际工程中前混式磨料水射流切割作业采用的磨料粒子体积浓度普遍都在10%左右[6]。流动中的颗粒与颗粒之间的相互作用以及颗粒对流体的作用不可忽视，须考虑液固两相的双向耦合作用，所以综合考虑选择固相满足连续介质假设的欧拉模型作为磨料水射流的两相流计算模型。欧拉模型的核心思想是将固相颗粒看成是拟流体，液相流体仍然满足连续介质假设，在同一坐标系下研究相互作用下的多种连续介质运动。对于颗粒流作为拟流体化也需要满足相应条件，常用方法是从粒间平均距离进行判断。其中粒间平均距离又与粒子负载、液固两相的物质密度比密切相关。

(1)粒子负载

粒子负载对液固两相流的相互作用具有重要影响，它定义为离散相与连续相的惯性力的比值。

(1)

式中：αd为离散相体积分数；αc为连续相体积分数；ρd为离散相密度；ρc为连续相密度；γ为离散相与连续相的密度比。

(2)粒子平距间距

根据Crowe等[7]研究表明，颗粒负载流中的固相粒子的粒间平均间距可按以下关系式表述。

(2)

(3)

式中：L为粒间平均间距；dd为粒子直径；β为粒子负载；γ为离散相与连续相的密度比。

结合本文研究内容，假设磨料粒子的密度ρd=2 600 kg/m3；直径dd=0.2 mm；体积分数αc=10%；液相水的密度ρc=998.2 kg/m3；体积分数αc=90%。将以上参数代入上式中得L/dd=1.74；L=0.35 mm。由此可知粒间平均间距很小，与粒子直径十分接近，颗粒间存在运动接触，其相互间作用力不可忽视，故可按连续介质原理将磨料粒子拟流体化处理，符合多相流欧拉模型的计算要求。

1.3 双流体模型基本方程

双流体模型中，固相与液相流体的速度均考虑由当地的平均量和随机分量组成，相关的连续性方程和动量方程有如下表达式[8]：

(1)流体相

(4)

(5)

(2)固粒相

(6)

(7)

式中：ρf=ρf(1-αp)为液相流体的局部密度；ρp=ρpαp为固粒相的局部密度；F为单位体积的相间相互作用力；Tp为固粒相的应力张量；Tf为流体相的应力张量。

1.4 模拟工况及边界条件

为了射流作业环境处于水下淹没状态，建立了装满水体的水下区域模拟淹没受限射流的密闭水下环境，模型由锥直型喷嘴与一个长20 cm，高25 cm模拟区域组成，其中喷嘴位于区域上方正中间处,如图1所示。

长江上游水流的平均流速一般在2～3 m/s左右，其中局部落差大的河道区域流速也可达5～6 m/s。结合河流中水流流速的实际变化情况，选取水流流速为0 m/s，2 m/s，4 m/s，7 m/s四种不同工况模拟计算淹没条件下的磨料水射流流场。由于环境流速一般为射流流速的1%左右，结合大部分河流水流情况，本文设置环境流速方向为从左到右且垂直于射流，忽略纵向流速对于射流的扰动。其中喷嘴的入口压力35 MPa，磨料密度2.60 g/cm3、体积浓度10%、直径0.2 mm，淹没水深深度2 m。

图1 模拟模型Fig.1 Simulating model

边界条件为：喷嘴入口设置为压力入口；顶部与大气环境相通，设置为压力出口条件；喷嘴及区域底部选择墙体壁面边界条件。通过对区域左侧的边界条件中设置不同的来水流速大小，概化模拟淹没水环境中动水环境下的磨料水射流流场变化，其中水流运动方向从左至右垂直区域左边界进入计算域。

本文所研究的磨料水射流为不可压缩流动，基于Fluent的压力求解器进行数值求解计算，其中离散方程组的求解算法采用Phase Coupled SIMPLE算法，选择的Realizablek-ε湍流模型属于高雷诺数湍流模型。其计算所得两相速度变化规律与林晓东等[9-13]研究成果相似。

2 模拟结果

2.1 不同环境流速下射流流场分布

结合图2～图5对比可知，淹没水环境中的水流流速大小对磨料水射流沿程发展造成了明显影响。磨料水射流处在静水环境中时，射流中液固两相的速度大小及方向呈现明显的对称分布，射流沿程伴随着与周围环境水体的接触卷吸作用下，磨料与水体的速度逐渐衰减，射流在冲击底部壁面后最终向两侧均匀扩散发展。当磨料水射流处在动水环境中，射流仍存在较为明显的等速核区域，但随着来水流速地不断增大，磨料水射流中的液固两相的速度大小分布逐步朝水流方向偏离，且水流流速越大，射流偏离越为明显同时伴随还产生了朝顺时针方向旋转的涡旋结构。

图2 水流流速0环境下的液固两相流场分布Fig.2 Flow field of the solid-liquid phase when flow velocity=0

图4 水流流速4 m/s环境下的液固两相流场分布Fig.4 Flow field of the solid-liquid phase when flow velocity=4 m/s

分析出现上述现象的原因在于临近喷嘴出口处的磨料水射流由于处于高速运动的状态，其速度越大，其能冲击能量就越集中，故越不容易受到外界环境的干扰。在逐渐远离的射流等速核的基本段内，由于射流能量的不断扩散衰减，射流流速随之减小，射流的集束性也随之减弱，故在面对迎面水流的冲击作用下，处于基本段中的射流出现了较为明显的偏离。同时，2 m/s的来水流速相比于整个射流的冲击速度而言并非一个量级，整个射流因其高速运动特性近似于坚硬的刚体结构，很大程度上阻碍了水流的向前运动，故在射流的卷吸作用与来水水流的冲击作用下，整个迎水面区域内的水体逐步发展呈现出了明显的涡旋结构现象。

图5 水流流速7 m/s环境下的液固两相流场分布Fig.5 Flow field of the solid-liquid phase when flow velocity=7 m/s

伴随着水流流速的不断增大，射流基本段区域内同样出现了明显的偏离与涡旋结构现象。区别在于，水流流速增加到4～7 m/s时，水流对射流冲击力有所增强，导致射流速度相对较低的基本段区域偏离程度也更为明显，整个射流迎水面涡旋结构也朝水流流动方向一侧进一步偏移。

2.2 不同环境流速下射流速度变化

2.2.1 中轴线位置速度对比

如图6所示，水下淹没环境中不同来水水流流速情况对喷嘴外流场中轴线位置上的液固两相速度大小存在一定影响。其中靠近喷嘴附近射流等速核区域中，磨料射流的速度大小并未随着迎面来水水流流速的增大有明显变化。但在喷距大于1 cm的范围内的射流基本段中，射流中液固两相的速度大小随着来水流速的增大呈现减小的趋势。结合前述内容中对于不同水流流速下的流场分析可知，射流在迎面水流的冲击作用下往往会整体发生一定的偏离，故相比处于静水环境下的射流而言，此时最大速度的射流并非保持在原中轴线位置处。

注：轴向距离起点0处为喷嘴出口截面轴心位置图6 不同水流流速情况下中轴线位置液固两相沿程速度变化Fig.6 Comparison of solid-liquid phase velocity on central axis under different flow velocities

2.2.2 等速核段水平截面位置速度对比

根据董志勇等[14-18]的研究，淹没射流的初始段所在的无量纲长度为l/d=5～7.5。这里选择l/d=6.5的水平截面位置为参照，对比分析不同水流流速条件下磨料水射流等速核阶段内的液固两相速度具体变化。

如图7(b)和图7(d)所示，y方向下的速度分量v主要代表了液固两相冲击能力。在相同喷距水平截面位置处，磨料射流中液固两相的运动速度峰值相差不大，速度大小分布随着水下来水流速的增大呈现出向右平移的现象。其中射流左侧(-2～0 mm)液固两相的速度大小随来水流速的增加呈逐渐减小的趋势；射流右侧(0～+2 mm)液固两相的速度大小随流速的增加呈逐渐增大的趋势。分析其主要原因在于射流左侧区域因处于迎水面，受到水流的直接冲击下，射流与周围水体的掺混紊动作用加剧，能量损失相对有所增加，所以出现了水流流速越高的情况下，射流左侧迎水面冲击速度更小的情况。同时，由于整个射流在左侧水流的冲击下，整体向右侧发生轻微的偏离，所以射流核心区域轴线位置附近的处于高速运动固相磨料以及液相水体在射流沿程不断发展扩散的过程中也会更多地向右侧偏离，且来水流速越大，偏离程度更明显，从而呈现出一种非近似完全对称的速度分布规律。

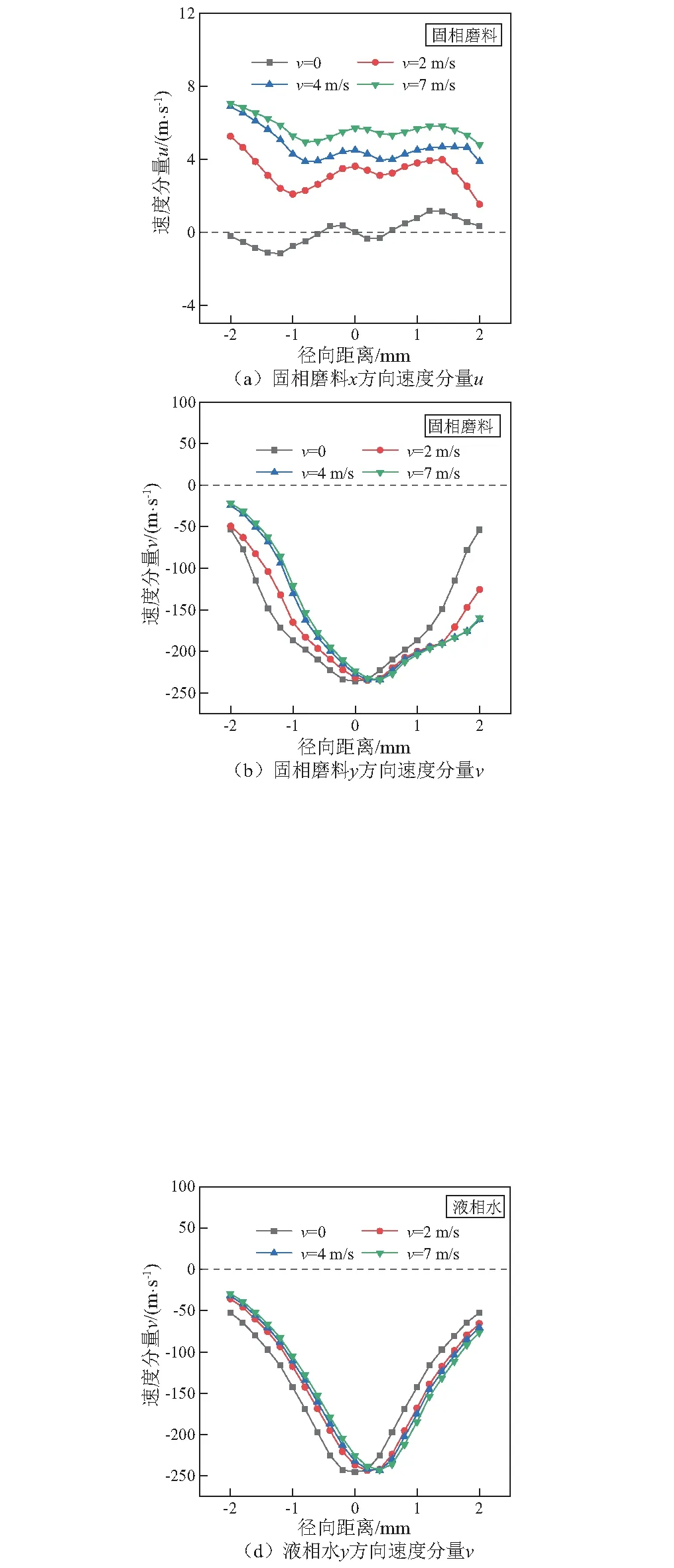
注：x方向速度分量水平向右为正；y方向速度分量竖直向上为正图7 无因次喷距l/d=6.5处水平截面位置液固两相速度矢量分布Fig.7 Velocity distribution of the two-phase on section where dimensionless jet distance l/d=6.5

综合图7可知，射流等速核内的液固两相冲击速度主要是基于竖直y方向上的速度分量ν为主。水下水流流速条件的改变会对整个磨料水射流各方向的速度矢量分布产生一定影响。伴随着水流速度的增大，液固两相速度分量u沿水流流动方向逐渐增加，其速度大小变化最大约10 m/s。同时，通过对比速度分量ν分布情况仍可以看出，液固两相的速度峰值并非在截面轴心处，射流整体向右侧发生偏移，且速度分量ν变化较小。

2.2.3 基本段水平截面位置速度对比

在基本段内，选取的截面应仍然保有一定的冲击速度，同时也受到区别于等速核的较为明显的偏移影响。因此选取无因次喷距为l/d=33的水平截面位置为参照，对比分析不同水流流速条件下磨料水射流基本段内的液固两相速度具体变化。

对于磨料水射流的基本段而言，射流逐步发展进入到了明显的扩散阶段，此时处于该阶段的射流在动水环境下的偏离现象相比相同条件下的等速核阶段而言更为明显。图8所示为处于射流基本段水平截面处径向距离(-4～12 mm)内的磨料水射流速度大小分布情况。当磨料水射流处于水流流速v=0的静水环境时，位于水平截面径向距离范围(-4～+4 mm)内的两相速度分布均呈现较好的对称性，其中速度峰值均在于中轴线位置处附近。当水下水流流速逐渐增大时，射流左侧的速度明显降低，速度峰值也随之明显减小，且位置偏离到径向距离+4 mm的位置处。在射流右侧区域范围(+4～+12 mm)内，动水环境下的射流速度却明显高于静水环境条件下。

分析出现上述现象的原因在于基本段内的射流集束性相比等速核段而言大大降低，在面对水下水流的迎面冲击作用下，射流方向偏离的更为明显，以致于相同水平截面位置处的射流扩散范围明显进一步扩大，射流在水平截面上的速度大小分布更为均匀，且射流沿程的最大速度并非保持在原中轴线位置处。故呈现出射流基本段内水平截面上速度峰值降低，射流扩散范围更大的现象。如图8所示，基本段内磨料水射流的冲击速度仍然主要是基于竖直y方向上的速度分量为主。相比射流的等速核区域而言，同样的水流流速条件下，基本段区域内射流的液固两相速度分量u沿水流流动方向的增量更为明显，其中固相磨料速度分量u最大增加可达约16 m/s，液相水体的速度分量u最大增加量约24 m/s。针对y方向的速度分量ν而言，整个速度大小分布明显向水流运动方向偏移，其速度峰值位置偏离到右侧径向距离+4 mm附近，且差值最大可达25 m/s。以上现象也进一步阐明了处于基本段内的磨料水射流偏离程度更大，更容易受水流条件变化的影响。

注：x方向速度分量水平向右为正；y方向速度分量竖直向上为正图8 无因次喷距l/d=33处水平截面位置液固两相速度矢量分布Fig.8 Velocity distribution of the two-phase on section where dimensionless jet distance l/d=33

3 结 论

(1)伴随着水下水流流速的增大，会导致射流在一定程度上朝水流方向逐步发生偏离。其中，射流能量相对集中的等速核段偏离程度很小，射流基本段偏离现象较为显著。

(2)射流整体的速度趋势主要由垂直方向速度来决定，对比静水条件下的垂向速度，在由环境条件流速下的垂向速度无论大小方向均会受到不同程度的影响。其中环境流速越大，所受影响越大。

(3)固液相速度的趋势在各自工况下都保持大致一致，但所受影响仍有可见的差别。

(4)若是只考虑能量损耗，最优靶距应选择在等速核末端，此时的射流具有最高的速度以及可以忽略的偏移，且环境流速并未对射流产生明显的影响。但根据侯亚康等[19]的研究成果，在淹没条件下若考虑到冲蚀深度以及回流冲击强度，可以预见当靶距达到基本段时，环境流速会对破岩效果产生较大影响，靶距越大影响越大，同时，也会对冲击点造成一定的偏移。对此，需要进一步的针对水流破岩方面的研究。

(5)本文采用的模拟方法并不能对磨料粒子运动做出详细的说明，需要PIV(Particle Image Velocimetry)等更进一步的试验方法研究。

(6)本文所采取的工况无法涵盖未来实际工程中可能出现的所有情况并对各种情况做出一个完整的认识，需要更深一步的研究。