涡激振动驱动的柱群结构俘获海流能的稳定性分析

罗竹梅，张立翔，张晓旭，李 丹

(1.昆明理工大学 冶金与能源工程学院，昆明 650093；2.昆明理工大学 建筑工程学院，昆明 650051)

海流能是海洋能的一种，其能量与流速的立方成正比，随时间变化较小。因此在海流流速稳定的区域，可获得稳定的海流能。但全世界大部分海流流速都低于1.5 m/s，这使得水下涡轮机的应用受到限制。涡激振动是一种非线性振动，其共振发生在固有频率附近，在较广的流速和雷诺数范围内都能产生有效振动，即使当水流速度低于0.1 m/s，仍能使刚性柱体结构产生振动[1]。这使得基于流体力学圆柱绕流涡激振动驱动捕获海流能，以此形成水力驱动系统进行发电成为一种选择。当涡激振动振幅较大，响应稳定，结构可从低速海流中俘获稳定的海流能。这一想法不仅对可再生海流能和低速河流能的利用有重要意义，对优化能源结构、促进清洁能源开发、发展低碳经济等也具有现实意义。

Bernitsas等对涡激振动驱动的海流能发电进行了研究，目前处于理论和实验阶段[2-4]。该团队建造了第一台能量转换器VIVACE(Vortex Induced Vibration for Aquatic Clean Energy)，将涡激振动产生的位移通过齿轮变速装置带动发电机产生电能[5]，但该转换器的振动结构仅有单圆柱组成。为了研究规模化俘获海流能的可行性，作者设计了耦合连接矩形布置的四圆柱结构作为能量转换器中的振动系统，并对该柱群结构的涡激振动及水动能俘获进行了前期研究[6-7]。结构中所有圆柱两端用刚性材料固定，各圆柱视为位置相对不变的整体，四圆柱结构整体为一个质量-弹簧-阻尼系统(见图1)。

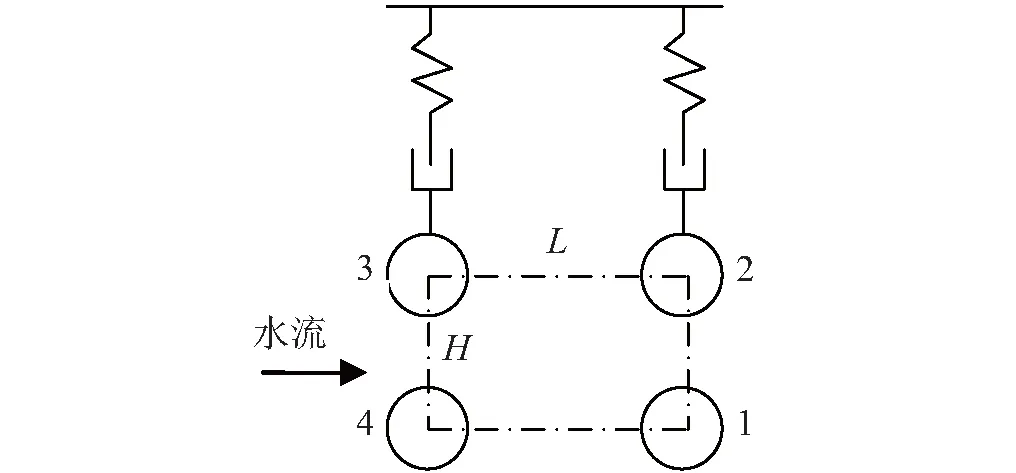
图1 耦合连接矩形布置的四圆柱结构模型Fig.1 The model of four coupling linked cylinders with rectangular arrangement

Lee等[8]用单圆柱振动结构俘获海流能的实验中，约化速度Ur为5～12时升力和位移呈正弦变化，各约化速度下升力与位移间存在明显的相位差Φ，能量转换稳定。对于论文中耦合连接的四圆柱结构，涡激振动响应必然受约化速度和间距比影响。不同约化速度下各圆柱升力响应是否规则，与位移间是否存在明显的相位差，能量转换是否稳定，响应时各圆柱对整个振动系统俘获能量的贡献多少等问题都有待研究。论文采用流固双向耦合数值方法，对图1所示的柱群结构在均匀来流下的自由涡激振动进行了模拟，通过对比较大较小两种约化速度时结构中各圆柱的升力特点，分析两种约化速度下各圆柱能量转换的稳定性及对柱群结构俘获能量的贡献大小。

1 数值方法和计算方案

1.1 流体控制方程

流体控制方程通过非定常不可压缩RANS方程求解。由于流固耦合边界随时间不断变化，为了描述不断变化的流体域，考虑网格移动速度，采用任意拉格朗日-欧拉(Arbitrary Lagrange-Euler，ALE)坐标系。ALE描述下流体的连续性方程和动量方程为

(1)

(2)

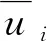
(3)

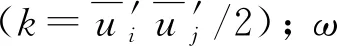
(4)

(5)

式中：1/2<γ<1；β=γ2/(2γ-1)；α=2-1/γ。该时间积分法采用时间步较少，总的求解时间更少。

1.2 结构控制方程

结构简化为一个如图1所示的质量-弹簧-阻尼系统，其动力响应采用基于实体单元的有限元方法进行离散，写成矩阵形式为

(6)

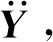
离散后的流体和固体模型通过流固耦合求解器同时求解，耦合边界上应用位移协调条件、力平衡条件以及速度平衡条件，实现流体和结构双向耦合计算。

1.3 计算方案

根据前期研究中涡激振动结构参数对俘获能量的影响结果，机械耦合四圆柱振动结构采用具有较高能量俘获效率的参数：质量比m*=3、阻尼比ζ=0.08、质量阻尼比m*ζ=0.24；固有频率fn,w=0.7，圆柱直径D为0.1 m。设置四个符合海洋环境的流速U：0.4 m/s，0.6 m/s，0.8 m/s和1.0 m/s，相应于两个较小约化速度Ur=5.71和Ur=8.57和两个较大约化速度Ur=11.43和Ur=14.29。计算的雷诺数范围为(0.4～1)×105，该范围属于TrSL3雷诺数区域，此区域内波动升力系数较大，能产生较大的振动幅值[9]。对表1中12种组合间距比方案进行涡激振动模拟计算。为模拟真实海流，取流体密度ρf=1 025 kg/m3,海水运动黏度ν=1.006×10-6m2/s[10]。

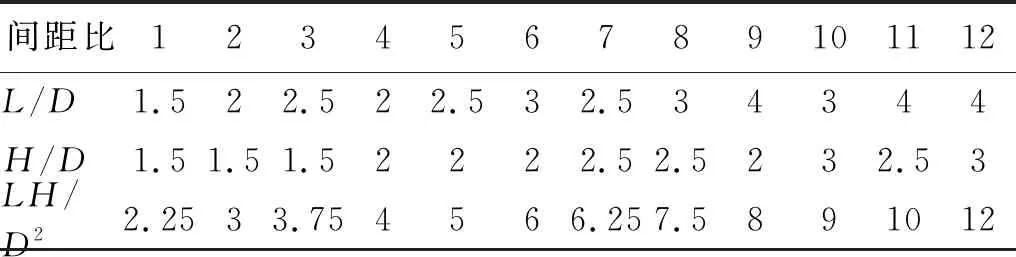
表1 间距比方案Tab.1 Cases of spacing ratio

1.4 俘获能量P

由四圆柱组成的振动系统其涡激振动趋于稳定时响应可近似为定常态的谐波振动，呈正弦规律变化，与升力之间存在一个相位差Φ。单位长度圆柱系统横向位移y(t)和升力Fl(t)表达成

y(t)=Asin(2πfext)

(7)

Fl(t)=Flsin(2πfext+Φ)

(8)

式中：A为振幅；fex为激励频率；Fy为升力幅值。

单位时间单位长度圆柱系统从流体中获取能量P为

(9)

由式(9)可知，振动系统从水流中俘获的水动能与振幅A、激励频率fex，升力幅值Fl以及相位角Φ有关。若上述四个参数响应值稳定，则可获得稳定的海流能。

2 结果分析

2.1 振幅响应特征

图2给出四圆柱振动系统在不同组合间距比LH/D2下的振幅与频率响应。从图2可知，不仅横向和流向间距比影响耦合四圆柱振动系统的振幅响应，约化速度也是影响幅值的一个重要因素。各约化速度下，振动系统的响应幅值随LH/D2的变化相差较大。当Ur=5.71时，振幅比A*随LH/D2的增大有缓慢增加的趋势。Ur=8.57时，各横向和流向间距比下A*相差不大。但在两个较大约化速度Ur=11.43和Ur=14.29时，A*随LH/D2的变化趋势明显不同于较小约化速度下的结果。Brika等[11]在风洞中对串列布置的两圆柱进行实验发现，小间距比下，由于两圆柱间流体的相互干扰作用，下游圆柱产生更大的振幅。Hover等[12]对相同两圆柱进行涡激振动实验发现，当Ur高达17时，下游圆柱出现了较高振幅的驰振响应。实验中结构在Ur=14.29，LH/D2=2.25时也出现了高达1.56的振幅比。但在LH/D2=12时，其A*仅为0.53。这说明小间距比时，柱群结构类似于一个大的单柱体，下游出现交替的脱落涡，随着约化速度的增加，雷诺数也增加，振幅响应越大。但间距比的增加使得圆柱间的相互作用减弱，振幅降低。

图2 各组合间距比下的振幅比A*Fig.2 Amplitude ratios A* at different combined spacing ratios

图3为Ur=5.71 和Ur=14.29两约化速度时四圆柱振动结构横向位移幅值谱图。图中给出了LH/D2分别为3，5，7.5，10和12时的结果。由图3可知：各组合间距比下，振动结构横向位移频率单一，存在明显的峰值，说明系统在均匀海流环境下，涡激振动位移响应有稳定的振动周期。同一约化速度下，主频率随LH/D2呈略微增加趋势，但相差不大，说明即使横向和流向间距比发生变化，但结构的振动周期变化不大。大约化速度下圆柱间流场干扰作用受间距比影响明显，间距比越大，位移谱峰值越小，见图3(b)。

图3 不同LH/D2时的位移幅值谱图Fig.3 Displacement amplitude spectra at different combined spacing ratio LH/D2

2.2 较小约化速度下的升力特性

由图2和图3可知，耦合四圆柱结构响应在大小约化速度下相差较大。为了解较大和较小约化速度时结构及各圆柱俘获能量的稳定性及对结构俘获能量的贡献大小，对Ur=5.71 和Ur=14.29时结构的升力特性进行分析对比。

图4、图5和图6为Ur=5.71时，LH/D2分别为3，5和12时的位移和各圆柱升力系数Cli时程曲线及升力幅值谱图。此约化速度下，来流速度不大，结构位移及各圆柱升力随时间呈正弦规律变化，且还存在明显的相位差Φ，如图4(a)、图5(a)和图6(a)所示。但四圆柱的升力与位移的Φ值各不相同，说明各圆柱表面涡脱落不同步。三种间距比下，圆柱1、圆柱2和圆柱3的升力超前于位移提前达到峰值，Φ>0。根据P=πAFlfexsinΦ，圆柱从水流中俘获稳定能量；相反，圆柱4其升力滞后于位移达到峰值，Φ<0，振动的部分能量转移到水流中。但从整个振动结构总升力来看，其与位移间的相位角为正，即整个耦合四圆柱结构涡激振动时从水流中俘获水动能。三个组合间距比下各圆柱升力Fli(i=1，2，3，4)与位移y间的相位差ΦFli和总升力Fl与位移y间的相位差ΦFl见表2。

图4 四圆柱升力系数和位移时程曲线及各圆柱升力幅值谱图(Ur=5.71，LH/D2=3)Fig.4 Time series of displacement and lift force coefficients of the four cylinders and the amplitude spectra of each cylinder’s lift force Fl(Ur=5.71,LH/D2=3)

图5 四圆柱升力系数和位移时程曲线及各圆柱升力幅值谱图(Ur=5.71，LH/D2=5)Fig.5 Time series of displacement and lift force coefficients of the four cylinders and the amplitude spectra of each cylinder’s lift force Fl(Ur=5.71,LH/D2=5)

通过对各圆柱升力的FFT频谱分析发现：振动由单一频率控制；无论在哪种间距比下，各圆柱的升力都存在明显的主频率，且该主频率与结构振动频率一致，对结构的振动起激励作用，如图4(b)、图5(b)和图6(b)。LH/D2=3时，各圆柱升力主频率相同，即fCl1=fCl2=fCl3=fCl4=0.70，与四圆柱结构的振动频率相等，振幅比A*=0.73；LH/D2=5时，各圆柱的升力主频率仍然与结构的振动频率都等于0.71，稍高于固有频率，这对于低质量比涡激振动而言，反而产生更高的振幅[13]，A*=0.80。大组合间距比LH/D2=12时，各圆柱的升力主频率与位移的主频率都等于0.74，更高于固有频率，振幅比达0.93。在出现“锁定”(Lock-in)且振幅和升力呈正弦规律变化的约化速度范围内(Ur=5～12)，各圆柱的升力按与位移相同的单一频率振动，说明各圆柱从水流中俘获的水动能或转移到水流中的机械能基本稳定。从升力谱峰值来看，较小约化速度时各圆柱对结构振动都起激励作用，这有利于水动能俘获计算。

图6 四圆柱升力系数和位移时程曲线及各圆柱升力幅值谱图(Ur=5.71，LH/D2=12)Fig.6 Time series of displacement and lift force coefficients of the four cylinders and the amplitude spectra of each cylinder’s lift force Fl(Ur=5.71,LH/D2=12)

表2 升力与位移间的相位差Φ(Ur=5.71)Tab.2 Phase difference between lift force and displacement

2.3 较大约化速度下的升力特性

从图2(a)可知，Ur=14.29时耦合四圆柱振动结构产生了高达1.56的最大振幅比。此时结构中各圆柱升力响应是否和较小约化速度下的结果一样具有规则的正弦波动？与位移间是否也存在明显的相位角？各圆柱在振动中能否俘获稳定的水动能？对结构振动贡献如何？通过图7、图8和图9的分析可以找到答案。图7、图8和图9为Ur=14.29时各圆柱升力系数Cli时程曲线、位移时程曲线及各圆柱的升力Fl幅值谱图。LH/D2=3时，此时横向和流向间距小，由于来流速度较大，雷诺数较高(Re约为105)，间隙流对圆柱间强烈的干扰作用导致了不规则的水动力，各圆柱的升力时程很不规则。从图7(a)发现，虽然各圆柱升力时程不规则，但位移却呈规则的正弦波动，且位移具有较高的振幅值及稳定的振动频率fosc，fosc=0.81。

频谱分析显示：图7(b)中，下游圆柱1有三个频率成分，圆柱2有四个频率成分，而上游圆柱3和圆柱4也分别有两个和三个频率成分，这些频率成分中有主频，也有2次、3次甚至4次谐波。圆柱1的主频为1.62，为振动频率的2倍，对结构振动起干扰作用。从升力谱峰值来看，圆柱2、圆柱3和圆柱4的升力频率中含有振动主频0.81，且幅值较高，对结构振动起激励作用。

由图8和图9可知，约化速度Ur=14.29时，随着横向和流向间距比的增加，各圆柱升力系数Cli的时程曲线逐渐趋于规则。间距比越大，上游圆柱3和圆柱4受下游圆柱的干扰作用越弱，其升力时程曲线越趋于正弦规律波动，下游圆柱受上游圆柱脱落涡不规则重附影响越小，其升力波动越趋于规则，但仍不呈正弦规律变化。LH/D2=5和LH/D2=12时，上游圆柱3、圆柱4的升力主频随着间距比的增加越来越明显，分别为0.83和0.85，与图3(b)中相应组合间距比下的振动频率fosc相同。且升力谱峰值明显大于下游圆柱1和圆柱2，对结构振动贡献较大。对比图7(b)、图8(b)和图9(b)发现，无论哪种间距比，圆柱1与振动频率相等的升力谱峰值都很小，对整个系统的共振作用也很小；而圆柱3和圆柱4对共振的贡献最大，其次为圆柱2。综上所述，较大约化速度下，结构中各圆柱升力波动不规则，升力位移间的相位角不明显，各圆柱俘获水动能不稳定，上游两圆柱对结构振动起主要作用。因此，对海流能发电涡激振动驱动的多圆柱结构，为了各圆柱俘获的水动能稳定，不宜采用较大的约化速度。

图7 四圆柱升力系数和位移时程曲线及各圆柱升力幅值谱图(Ur=14.29，LH/D2=3)Fig.7 Time series of displacement and lift force coefficients of the four cylinders and the amplitude spectra of each cylinder’s lift force Fl(Ur=14.29,LH/D2=3)

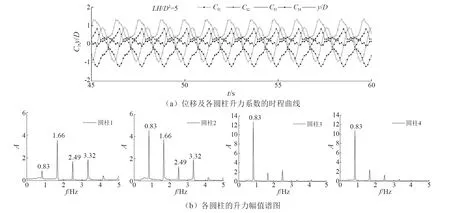
图8 四圆柱升力系数和位移时程曲线及各圆柱升力幅值谱图(Ur=14.29，LH/D2=5)Fig.8 Time series of displacement and lift force coefficients of the four cylinders and the amplitude spectra of each cylinder’s lift force Fl(Ur=14.29,LH/D2=5)

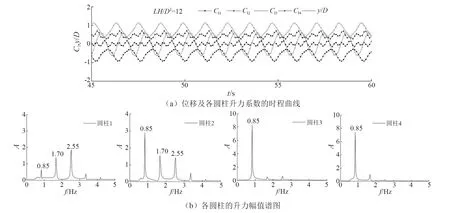
图9 四圆柱升力系数和位移时程曲线及各圆柱升力幅值谱图(Ur=14.29，LH/D2=12)Fig.9 Time series of displacement and lift force coefficients of the four cylinders and the amplitude spectra of each cylinder’s lift force Fl(Ur=14.29,LH/D2=12)

4 结 论

本文对海流能发电涡激振动驱动的耦合连接四圆柱在均匀海流下的自由涡激振动进行了模拟，设计了不同的组合间距比和约化速度方案。分析了不同方案下结构的幅值响应，针对较大较小约化速度幅值响应结果相差大这一现象，通过分析位移幅值谱图、升力特性、相位差等结果来确定结构振动时各圆柱能量贡献的稳定性及大小。研究结果表明：

(1)较小约化速度下柱群结构的振幅幅值受组合间距比影响较小，而较大约化速度时不同组合间距下振幅幅值相差很大。

(2)较小约化速度时，耦合四圆柱结构在不同间距时各圆柱升力与位移相位角Φ不同，有明显的主频且呈较规则的正弦规律变化，四个圆柱都对结构的振动起激励作用，各圆柱俘获的水动能或转移到水流中的机械能相对稳定。

(3)较大大约化速度下，各圆柱升力波动不规则，升力频率成分复杂，俘获的水动能不稳定，上游两圆柱对结构振动的贡献比下游两圆柱大。

(4)若使四圆柱柱群结构稳定俘获海流能，不宜采用较大的约化速度。