一种分析非均匀厚度1-3型压电复合材料换能器性能的方法

孙瑛琦，曾德平，张春杨，许佳琪，张菁霓，龚 洋，何 倩，高雪梅，杨增涛

(重庆医科大学 生物医学工程学院 省部共建国家重点实验室培育基地—重庆市超声医学工程重点实验室 重庆市生物医学工程学重点实验室 重庆市微无创医学协同创新中心，重庆 400016)

压电复合材料是指由压电陶瓷和聚合物按一定的连通方式、一定的体积或质量比，以及一定的空间几何分布复合而成的材料。根据连通性的不同，两相压电复合材料可分为10种类型，分别为0-0型、0-1型、0-2型、0-3型、1-1型、1-2型、1-3型、2-2型、2-3型和3-3型，其中对1-3型压电复合材料的研究最深入。1-3型压电复合材料结合了压电陶瓷和聚合物的优点，与大多数压电陶瓷相比，1-3型压电复合材料具有较低的声阻抗、较高的耦合系数、较低的机械品质因数和介电损耗，并且在设计方面具有更好的灵活性[1-2]。如今，1-3型压电复合材料在生物医学换能器、水下应用和微型定位系统等领域中得到广泛的应用[3-5]。

将1-3型压电复合材料设计成非均匀厚度压电片可以增加换能器的工作带宽，还可以实现超声波聚焦[6-11]。基于非均匀厚度1-3型压电复合材料片的特性，可将其作为一种宽带超声换能器，已被应用于水浸无损探伤、声波测井以及超声成像如：多普勒成像、弹性成像、灰度成像等领域，同时也可以作为聚焦超声波发射换能器，实现在水中及固体材料中的聚焦。

超声换能器性能参数的精确模拟在换能器设计过程中尤为重要。目前，换能器的常用分析方法有梅森(Mason)模型、克里姆霍尔兹(KLM)模型、压电振动模型[12-14]以及有限元法[15-16]等。前三种研究方法已被应用到分析和优化均匀厚度1-3型压电复合材料[17]，而无法直接用于分析非均匀厚度1-3型压电复合材料换能器，有限单元法可不受结构形状及材料的限制，但其模拟计算时耗时较长且无法解析表达出各参量之间的关系。因此，需要建立一种新的分析方法来分析非均匀厚度1-3型压电复合材料换能器的性能。

为分析非均匀厚度1-3型压电复合材料换能器的性能，本文提出了一种并联振子等效电路模型，即将非均匀厚度1-3型压电复合材料换能器看成并联的谐振器阵列，采用三维厚度伸缩振动模型对谐振器单元进行理论分析，并制作了非均匀厚度压电换能器的样品，分析对比理论及实验结果。对非均匀厚度压电换能器的动态特性进行建模。

1 等效模型建立

非均匀厚度1-3型压电复合材料片示意图，如图1所示。该换能器被设计为平凹形状，其厚度沿径向逐渐增加，其中凹面的曲率为R，边缘厚度为H，压电片的直径为d。

图1 非均匀厚度1-3型压电复合材料片示意图Fig.1 1-3 piezoelectric composites harvester of gradually varying thickness

对于1-3型压电复合材料，其横向应力被聚合物介质吸收，环氧树脂相的剪切模量远远小于压电相的纵向弹性模量，各个PZT柱之间的相互耦合很小[18-19]，因此，当1-3型压电复合材料制作成非均匀厚度压电片时，可以认为它是由不同厚度的谐振器阵列并联组成。在施加超声压力时，这些谐振器阵列可以沿着厚度方向独立地进行振动。因此，在前期建立的1-3型压电复合材料厚度伸缩模型[20-23]的基础上进行完善与改进，建立并联振子等效电路模型对非均匀厚度1-3型压电复合材料进行理论分析，如图2所示。

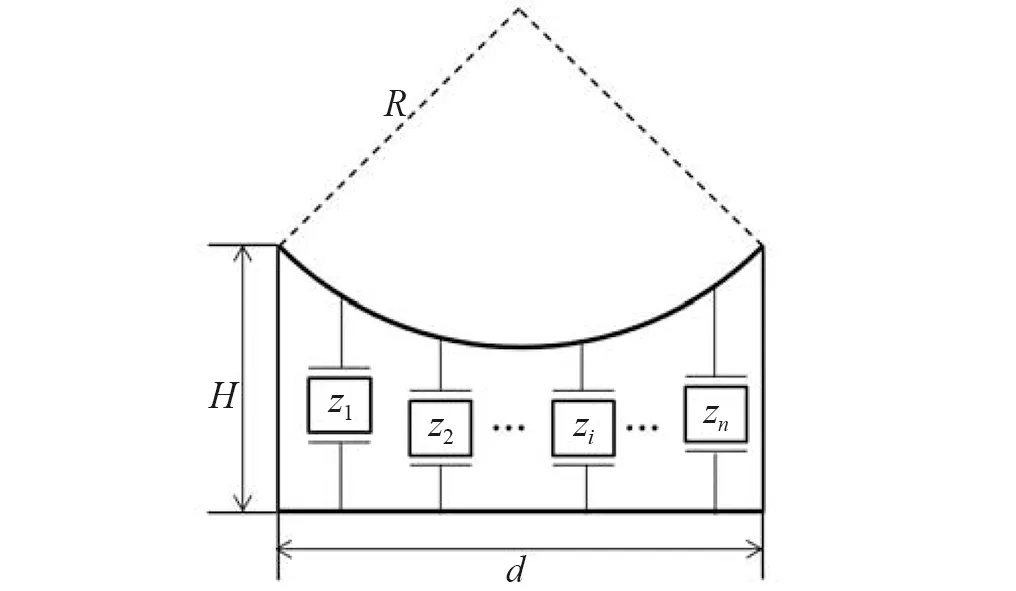
图2 非均匀厚度1-3型压电复合材料的等效电路模型Fig.2 The equivalent circuit model of non-uniform thickness 1-3 piezoelectric composite transducers

2 振动及阻抗分析

由谐振器阵列并联而成的非均匀厚度1-3型压电复合材料的总阻抗可以表示为

(1)

式中：Zi为单个振荡器单元的阻抗。

以厚度为2hi的振荡器单元为例，其振动模型如图3所示。有研究表明1-3型压电复合材料可以作为有效的均匀介质处理[24]。因此，提出了一种采用大体积压电陶瓷板代替1-3型压电复合材料的分析模型，该板由x=±hi的两个平面界定，并且这两个表面之间无牵引力。极化方向P沿板的纵向，即图3中x3方向。

图3 谐振器单元振动模型Fig.3 The vibration model of the oscillator unit i

1-3压电复合板的三维线性压电控制方程和界面边界条件方程可以写成[25]

(2)

式中：ui为位移矢量；Tij为应力张量；Sij为应变张量；Ei为电场矢量；Di为电位移矢量；φ为电势。cijkl，ekij和εij分别为有效弹性常数、压电常数和介电常数；ρ为有效的质量密度；ω为角速度；V为上下两个界面的电势差。

对于在x3方向上极化的1-3个压电复合材料，考虑到板的厚度拉伸振动仅取决于u3，位移及电势表达式为

u3=u(x3)eiωt,u1=u2=0,φ=φ(x3)eiωt

(3)

上式描述的模式可由三维线性压电方程表示，并且可简化为一维模型。对式(2)和式(3)进行推导和简化，可得到单个谐振器单元的电阻抗的解析解

(4)

将式(4)代入式(1)，可以得到非均匀厚度1-3型压电复合材料总阻抗的解析解为

(5)

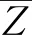
3 实验结果与讨论

为验证模型的正确性，采用锆钛酸铅(PZT-5A)和环氧树脂两种材料，通过“切割-填充法”[26]制作1-3型压电复合材料片，再通过特殊工艺将压电复合材料片中的一面制作成凹面，另一面为平面，制作出非均匀厚度的1-3型压电复合材料样片，如图4所示。其材料参数和几何参数如表1所示。

对于如图4所示的凹球面形状换能器，通过简单几何关系可以得到hi与半径r之间的关系

(6)

式中：R为压电片凹面的曲率半径；H为压电片的边缘厚度；d为压电片的直径。

表1 PZT-5A和环氧树脂的材料参数及压电片的几何参数Tab.1 Material parameters for PZT-5A and epoxy,and geometry parameters for non-uniform thickness disc

图4 非均匀厚度1-3型压电复合材料样片Fig.4 Samples of non-uniform thickness 1-3 piezoelectric composite disc

在1-3压电复合材料片的厚度伸缩振动数值计算中，存在黏性阻尼，使用c33(1+iQ)代替有效弹性常数c33。在建模中，通常使用Q表示整个结构阻尼的单个阻尼系数。对于该样本，在理论分析中令Q=0.06以匹配实验结果。

使用阻抗分析仪(Agilent 4294A)对非均匀厚度1-3型压电复合材料样片的阻抗进行了测量，将实际测量结果与理论结果进行对比，如图5所示。图5(a)、图5 (b)分别为幅频特性曲线和相频特性曲线。

如图5所示，实验结果和理论结果之间一致性相对较好，偏差较小，证实本文提出的一种采用并联振子等效电路模型计算非均匀厚度1-3型压电复合材料换能器性能的方法是可行的。

由图5(a)可知，阻抗的极大值点为反谐振频率fa，阻抗的极小值点为谐振频率fr。由式(1)可得，fa和fr分别由换能器内最小厚度及最大厚度的振荡器单元决定。文献[27-28]表明通过将谐振频率接近的多个谐振器并联，可以很大程度上增加换能器的带宽。依据电路原理可知，当两个阻值相差悬殊的电阻并联后，并联的总阻值更接近于小电阻值。在厚度振动模式下，谐振单元的厚度对谐振频率及阻抗的影响如式(4)所示。当将换能器设计成非均匀厚度时，并联的谐振单元的阻抗幅频曲线的趋势是相似的，彼此的谐振频率不同但阻抗极值接近，因此导致并联电路总阻抗频响曲线在较宽的频率范围内较为平坦，使其工作带宽明显增加，因此该换能器的频率差Δf(Δf=fa-fr)由换能器的厚度差决定，这与传统的均匀厚度1-3型压电复合材料阻抗特性明显不同。

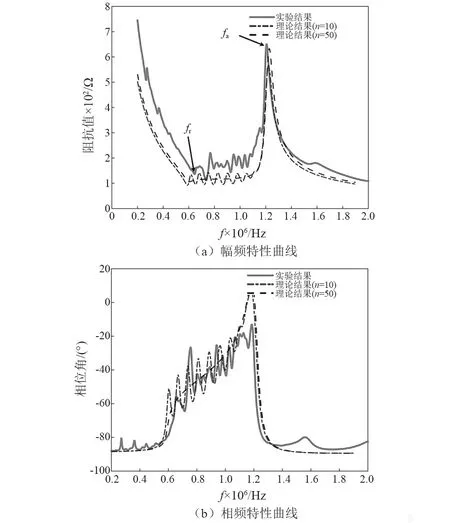
图5 实测结果与理论结果比较Fig.5 Electrical impedance comparison between theoretical and experimental

如式(1)和式(5)所示，n为换能器半径长度范围内谐振单元的个数，为使理论计算中几何尺寸与样品实测的厚度相吻合，需使n等于换能器半径长度范围内PZT柱的个数。图4所示换能器样品的半径长度范围内PZT柱的数量为10个，因此在计算中取n=10。如图5所示，当n=10时，在fr和fa范围内的理论结果及实测结果均出现起伏现象，但随着n值的增加，即当换能器PZT柱越密集时，其阻抗的曲线会变得更为平滑。因此，换能器的厚度不连续会造成其阻抗曲线的起伏。

从图5(a)可知，理论结果与实测结果还存在一定的偏差，主要表现在理论频率差Δf略大于实际频率差，理论阻抗值略小于实际阻抗值，产生这一现象的主要原因如下：①非均匀厚度1-3型压电复合材料换能器样品的PZT柱横向尺寸为0.8 mm×0.8 mm，PZT柱不够密，造成厚度不够连续；②在设计等效模型时，由于横向剪切力比较小，没有考虑横向剪切力带来的影响；③此外，也没有考虑换能器的制作工艺、导线及焊点等因素所带来的影响。

4 结 论

本文提出了一种用于分析非均匀厚度1-3型压电复合材料换能器性能的方法。采用并联振子等效电路模型及三维厚度伸缩振动模型，建立了分析非均匀厚度1-3型压电复合材料换能器性能的方法，得到了非均匀厚度压电复合材料阻抗的解析解；设计并制作了非均匀厚度压电换能器，并通过试验进行验证。结果表明，理论及试验结果吻合性较好，并联振子等效电路模型可用来计算非均匀厚度1-3型压电复合材料换能器的阻抗；非均匀厚度换能器的1-3型压电复合材料换能器的工作带宽由其厚度差决定。研究结果可为非均匀厚度宽带换能器的设计提供参考。