固结磨料确定性研磨表面生成建模与实验分析

林 彬，李凯隆，曹中臣，姜向敏，黄 田



固结磨料确定性研磨表面生成建模与实验分析

林 彬1, 2，李凯隆1, 2，曹中臣1, 2，姜向敏1, 2，黄 田2

(1. 天津大学先进陶瓷与加工技术教育部重点实验室，天津 300350；2. 天津大学机械工程学院，天津 300350)

基于CCOS技术原理，提出高效、高可控性的固结磨料确定性研磨工艺．通过线研磨实验发现采用中心供给研磨液方式相比于传统四周供液方式有利于提高加工效率及表面质量．分析了工艺参数对加工后表面硬度的影响，通过扫描电镜观察研磨后的表面形貌，分析固结磨料研磨的材料去除机制．通过不同参数线研磨实验验证了材料去除率与工具转速、载荷、时间呈线性关系，表明固结磨料研磨工艺的材料去除过程符合CCOS的卷积迭代原理．基于晶胞理论和磨粒粒径均匀的假设，建立了固结磨料研磨垫表面形貌的仿真模型．同时，模型考虑了磨粒浓度、磨粒粒度、研磨垫形状参数的影响．在固结磨料研磨垫形貌仿真数据的基础上，基于硬脆材料去除机理以及研磨垫与工件微观接触模型，考虑工件表面的力学性能，建立了一定参数条件下研磨垫与工件的接触间隙计算模型，进而建立了单点研磨去除斑模型．通过定点研磨实验验证了不同压力、转速、时长条件下单点研磨去除斑模型的准确性．将连续的研磨轨迹进行离散，考虑研磨垫形状、磨粒的尺寸和浓度、研磨工具的转速和承受的载荷、轨迹参数建立了总去除量与单点研磨去除量的卷积运算关系，提出固结磨料确定性研磨表面生成模型．开展不同参数下面研磨实验与表面仿真．结果表明，固结磨料确定性研磨表面生成模型能很好地预测不同参数下研磨去除的深度和研磨表面的残留误差，提高固结磨料研磨工艺的可控性．

固结磨料研磨；工艺参数；表面生成模型；轨迹

研磨是光学器件制造中获得高质量表面的关键技术，随着纳米电子学、新材料科学和光电子信息产业的迅速发展，对硬脆材料的研磨加工过程的平坦性、均匀性和可控性提出了更高的要求[1-2]．游离磨料研磨技术是目前国内外研磨加工的主要手段，但针对高效、高精度的加工要求，游离磨料加工有两个缺点[3]：①磨粒分布不均、研磨垫磨损、磨料轨迹不确定导致去除过程难以控制[4]；②为降低亚表面损伤，通常采用软磨料来研磨硬质表面，游离的磨料无法提供较大剪切力，导致加工效率低下．固结磨料技术是在传统游离磨料的基础上发展起来的高效、低成本、清洁的精密加工技术[5-6]．美国3M公司于1998年第1次将固结磨料技术用于芯片加工，实现了高效、快速表面平坦化[7]．Gobena等[8]使用3M公司的固结金刚石磨料研磨垫，采用去离子水作为研磨液，针对多种硬脆材料进行了研磨实验，发现固结磨料研磨去除效率高，同时可达到0.158μm的表面粗糙度．南京航空航天大学的朱永伟等[9]、李标等[10]针对固结磨料研抛的去除效率、表面质量、亚表面损伤以及抛光垫组分对抛光垫特性及加工性能的影响展开探究．研究结果表明，固结磨料的去除效率为游离磨料的2～3倍，固结磨料加工后表面的亚表面裂纹层深度远小于游离磨料．综上所述，固结磨料研磨是研磨技术发展的重要方向之一．

从美国Itek公司的Rupp于20世纪70年代采用较小的磨头，在计算机控制下，以特定路径、速度在工件表面运动的计算机控制光学表面成型技术(CCOS)[11]后，CCOS一直作为高精度、大口径球面、非球面光学元件的主要加工手段之一．传统的固结磨料研磨工艺主要使用平面研磨机对工件进行研磨加工[2]，金刚石磨粒被压入金属或树脂研磨垫基体中，工件被工具压在研磨垫上，通过工作台的自转和工件公转实现材料去除[8]．这种传统研磨工艺导致工件被加工面去除不均匀，且工件尺寸受设备限制，无法加工大口径工件．将CCOS技术可控性高、应用范围广的优势与固结磨料加工效率高的特点相结合，可以有效克服传统固结磨料的工艺缺陷．

许多学者致力于通过建模和仿真的方式，预测不同工艺参数条件下的材料去除率、表面质量. Agarwal等[12]、Sun等[13]针对陶瓷、半导体材料的磨削工艺，在磨粒切深符合Rayleigh概率密度分布的假设基础上，通过理论推导得出表面粗糙度值与进给速度、切深等参数的关系，以此来预测加工后表面的粗糙度．李军等[14]计算了固结研磨过程中有效磨粒数量，基于力平衡原理求出单颗磨粒的平均切入工件深度，建立了固结磨料研磨K9 玻璃表面粗糙度预测模型，实验结果表明模型能够成功预测不同加工参数下的表面粗糙度．Wang等[15]定量讨论了在采用固结磨料研磨碳化硅时，单个金刚石磨粒在碳化硅表面的切深与表面粗糙度和材料去除率的关系，建立了材料去除率、表面粗糙度的数学模型．上述研究主要是建立去除效率或表面粗糙度与加工参数的关系，然而磨粒的运动轨迹对工件表面平整度和粗糙度有重要影 响[16]，上述模型无法反映研磨轨迹对表面质量的影响．Wang等[17]提出了一种预测超声振动辅助磨削(UAG)表面形貌的新方法，通过模拟砂轮表面形貌，计算磨粒运动轨迹，建立了磨削表面生成模型，揭示了表面形貌、磨削力、材料去除率和超声振动特性之间的关系，但缺乏相关实验验证模型的准确性．Zhao等[18]在确定砂轮各个晶粒与工件的微观相互作用的基础上，考虑砂轮形貌和磨削运动的随机性而建立了加工后表面形貌的预测模型，能够预测加工后表面的粗糙度、轮廓不平整度和波纹度，并通过一系列实验验证了模型的准确性．该模型能很好地预测加工参数对磨削表面质量的影响，但对加工轨迹的影响分析不足．

综上所述，针对游离磨料加工的缺点以及传统固结磨料工艺的限制，通过结合CCOS技术与固结磨料研磨技术，提出高效、可控的固结磨料确定性研磨工艺．同时，针对各个学者在磨削、研磨工艺建模过程中的不足，在硬脆材料去除机理的基础上，考虑固结磨料确定性研磨工艺过程中研磨垫形状、磨粒的粒径和浓度、研磨工具的转速和承受的载荷、工具轨迹参数，建立一套能够预测材料去除率、研磨深度及残留误差的研磨表面生成模型．

1 固结磨料确定性研磨工艺探究

1.1 固结磨料确定性研磨工艺介绍

固结磨料确定性研磨工艺是将传统的CCOS工艺与固结磨料工艺相结合，提出一套实现硬脆材料表面快速成型的研磨工艺．CCOS工艺是一个通过面型修整以获得表面质量符合标准的工件的工艺过程，而固结磨料确定性研磨工艺是作为抛光工艺的前一道工序，力求通过固结磨料高去除效率的特点，选择合适的加工轨迹以及工艺参数，快速实现表面的平坦化，同时降低表面的加工残留误差，衔接后续工艺的过程．固结磨料确定性研磨工艺过程如下：测量工件的初始形貌；通过表面生成模型预测不同工艺参数、轨迹参数加工后工件的表面形貌；根据仿真结果选择最优的参数进行加工．工艺设备如图1所示，6自由度混联机器人数控抛光系统可以满足大口径非球面光学元件的加工需要．

传统固结磨料研磨工艺如图2所示，研磨液通过喷嘴从工件四周向供给，由于工具旋转产生的离心力作用，研磨液很难进入到工件中心区域．固结磨料确定性研磨工艺采用的自主设计的小磨头工具如图3所示，是在传统小磨头工具的基础上进行了改进，可以满足研磨液从中心供给的要求．从中心供给去离子水经过中心管路均匀连续地运送到研磨垫和工件之间，带走摩擦所产生的加工热量，同时，相比于传统的四周供液工艺，中心区域供液充足增加了加工区域水的润滑效果，减缓了研磨垫的磨损，提高了研磨去除率的稳定性．

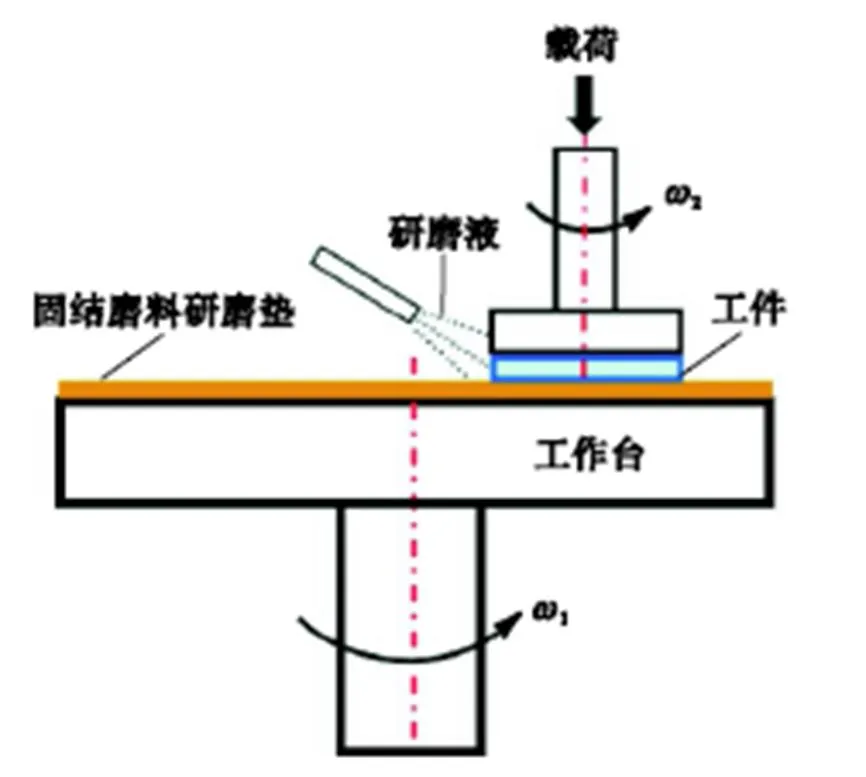
图2 传统固结磨料研磨工艺示意

图3 中心供液研磨工具示意

1.2 机理研究

传统的研磨工艺多采用四周供液的方式，为了验证研磨工具头采用中心供液的方式相对于传统四周供液方式的优势，设计如表1所示的实验，按照表中的参数设置小磨头工具的转速、工具载荷以及工具的进给速度，同时，分别采用中心供液、四周供液方式进行线研磨实验，对比单位时间的去除体积以及加工后的表面粗糙度．

表1 不同供液方式线研磨实验参数

Tab.1 Line lapping experimental parameters of different liquid supply methods

实验采用的固结金刚石磨粒的研磨垫如图4所示，主要成分为羟基碳氢化合物10%以上，聚酯纤维80%以上，金刚石磨粒的质量浓度为0.38g/cm3，粒度为4μm，镶嵌在16个2.3mm×2.3mm的凸起上，其他区域不含有磨粒，中心打孔便于中心供液，冷却液为去离子水，流量为5mL/s．实验样件为直径150mm的熔融石英玻璃，实验时，需将固结磨料研磨垫粘结在图3所示的研磨工具头上，再将整个研磨工具装夹在图1所示机器人的末端执行机构上，通过计算机控制小磨头工具以表1中各组的参数进给30mm长的直线，采用两种供液方式，进行6组实验.

图4 固结磨粒研磨垫

选用Nanovea白光干涉三维轮廓仪测量实验结果三维形貌，量程选择0～300μm，采样步长选择1μm，测量参数为600r/min、35N、3mm/s线研磨实验的工件表面三维形貌如图5所示，取中间位置平行于短边方向的截面轮廓如图6所示．

图5 工件表面三维形貌

图6 截面轮廓

计算中心截面轮廓的横截面积，取线研磨实验结果中间长度为10mm的区域求解去除体积，则研磨去除体积

(1)

测量计算各组线研磨实验结果的单位时间去除体积以及测量多条实验结果中间截面轮廓曲线，取截面轮廓曲线的中段10mm测量表面粗糙度均值(Ra)，如图7所示．

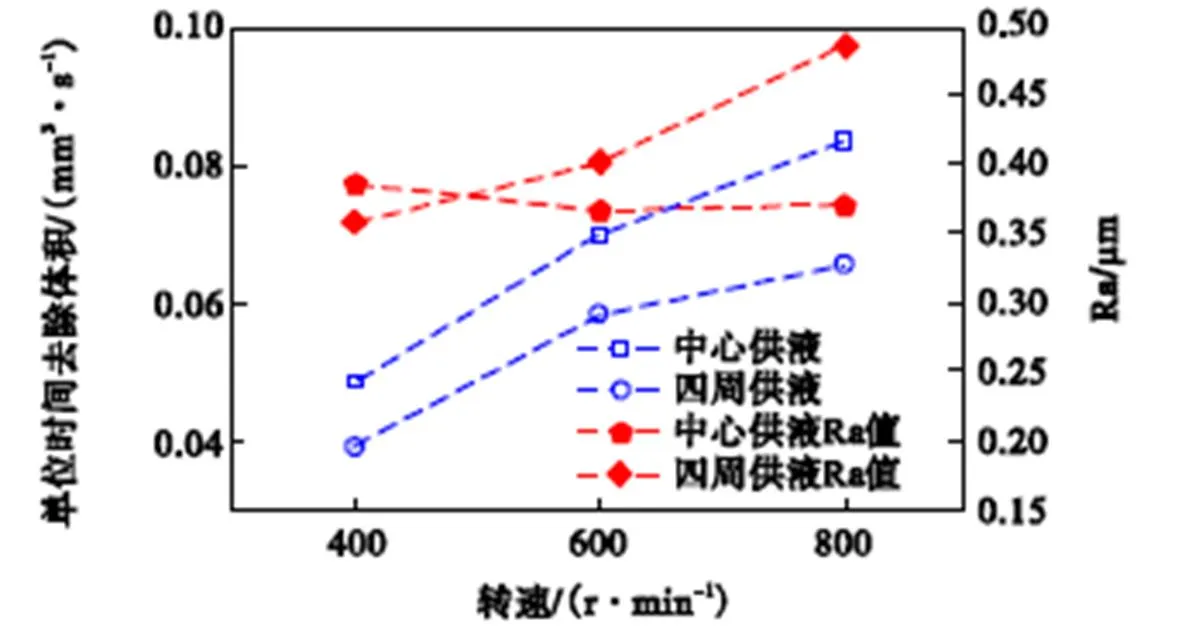
图7 不同供液方式实验结果对比

由图7可知，中心供液方式的材料去除率大于四周供液，原因是因为中心供液方式可以减缓研磨垫磨损，使材料去除率更加稳定，而在四周供液的方式下，磨头高速转动，离心力的作用使研磨液无法进入中心区域，导致研磨垫磨损严重，表层磨粒脱落过快，材料去除率下降．相比于四周供液，中心供液方式下转速变化对粗糙度的影响不大．而在四周供液方式下，表面粗糙度随转速增加而增大，因为随着转速增大，中心区域的供液量越来越不足，导致研磨碎屑无法及时排出，使表面质量恶化．因此，采用中心供液的方式更有利于提高加工效率和表面质量．

为了探究两种供液方式下不同的压力、转速对加工前后材料表面硬度的影响，以及研磨材料去除机制，取直径为60mm的熔融石英样件，按照中心、四周两种供液方式进行如表2所示参数的线研磨实验，其他实验参数不变，实验过程如前所述，然后对加工后表面使用显微硬度计、扫描电镜进行观察测量．

使用HXD-1000TMC/LCD显微硬度计，采用金刚石压头，实验力为9.807N，取多个测试点，测量不同实验参数加工前后表面维氏硬度值，求取平均值，对照不同压力、转速分析实验前后硬度(HV)变化，如图8所示．

表2 探究去除特性线研磨实验参数

Tab.2 Line lapping experimental parameters for explor-ing the removal charactericstics

图8 研磨前后的表面硬度

硬度是硬脆材料一个重要的力学性能指标，维氏硬度是一个重要的力学性能指标，表明材料是否容易产生塑性变形．熔融石英工件加工前后表面硬度会发生变化，一方面可能因为工件经过了多次铣磨，或之前反复地进行研抛实验，造成表面晶体发生相变，存在几微米的加工变质层，因此表层材料的硬度较大，而经过研磨后变质层变薄或被去除，加工前后的硬度发生了较大变化；另一方面可能是因为研磨加工时工件表面受到磨粒切削力的作用，表面材料以塑性或脆性方式去除，引起晶体结构组织变化，形成加工变质层，导致工件表面硬度发生变化．当材料以脆性方式去除时，表层的硬度会随之降低；当材料以塑性方式去除时，会发生表面硬化，表层硬度变大．由图8的结果发现，经过研磨后表面硬度会降低，可以推测熔融石英玻璃的材料去除中存在脆性去除的方式．同时，对比图8中心与四周供液方式下表面硬度发现，四周供液方式下加工前后表面硬度变化更大，表明在四周供液方式下，研磨后表面性质发生变化大．由图8(a)观察不同压力对表面硬度的影响发现，在四周供液方式下压力增大会导致表面硬度迅速减小，而中心供液方式下硬度变化较小．由图8(b)观察不同转速对表面硬度的影响结果发现，转速越小，加工前后表面硬度值变化越大．

通过扫描电镜观察采用中心供液、加工参数为600r/min、25N、2mm/s的表面的微观形貌，结果如图9所示．观察图9(a)的图像发现，加工后表面有明显的磨粒滑擦留下的轨迹痕迹，观察图9(b)可以进一步分辨出研磨后表面的特征，黄色框标记区域较为平滑，无明显的凹坑存在，为塑性去除获得的表面；绿色框标记区域有形状复杂、不规则凹坑，是熔融石英玻璃表层崩裂、破碎的结果，为脆性去除获得的表面；蓝色框标记区域初步推测为研磨垫基体材料填充区域，可能是由于加工过程中研磨垫基体材料脱落，嵌入表层破碎区域的结果．为了验证这一猜想，分别对3个区域进行能谱分析，分析结果如表3所示．由分析得到的数据可知，Au原子存在是因为熔融石英玻璃导电性差，SEM观察前进行了喷金处理，绿色、黄色框区域为熔融石英玻璃，而蓝色框区域元素与其他区域差异较大，引入一定比例的O、F、Ce、C元素，研磨液为去离子水，不考虑化学作用，可以推测出杂质是研磨垫的基体材料，如羟基碳氢化合物、聚酯纤维等．

图9 扫描电镜图像

表3 元素分析结果

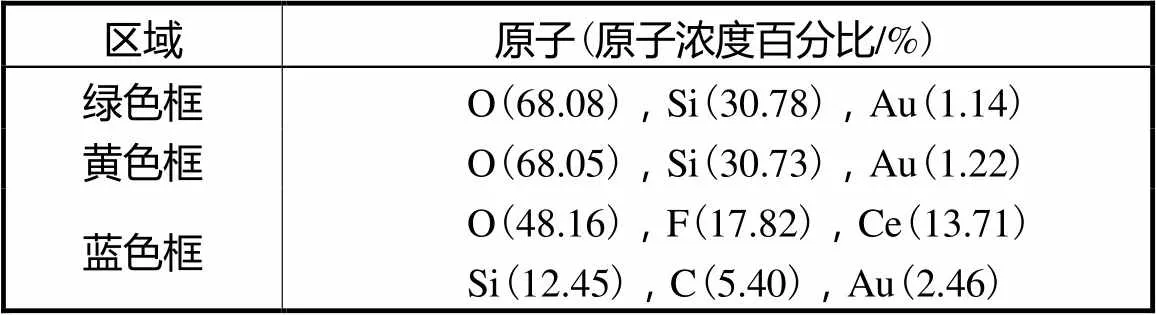
Tab.3 Elemental analysis results

观察图9(a)的表面形貌发现，几乎所有的脆性去除形成的破碎区域都填充了杂质，可以大致认为图中深灰色区域为塑性去除区域，灰白色区域为破碎区域，将图9(a)用计算机进行二值化处理，使形状复杂不规则的破碎面与完好表面区分开，如图10所示．计算得到表面破碎率为25.5%，即材料表面脆断面在平行于材料自由表面上的投影与材料的自由表面面积之比．可以得出结论：在一定参数条件下，固结磨料研磨材料去除为脆性去除与塑性去除综合作用的结果．

图10 工件表面形貌二值化图

(2)

式(2)揭示了总去除量与驻留时间、去除函数的卷积运算关系，去除函数又是由压力与速度等因素决定的．光学零件的抛光加工过程可以被简化成与速度、压力及时间有关的线性时不变系统，将单位响应和输入信号求卷积，就相当于把输入信号的各个时间点的单位响应加权叠加，即可得到输出信号．因此，由卷积线性迭代的原理知，压力、速度、时长与总去除量的关系是线性的．而在固结磨料确定性研磨过程中，去除过程是否可以等效为卷积过程可以通过实验探究研磨参数是否与去除量呈线性关系来进行验证．按照表4的参数进行实验，为保证实验条件的一致性，每组在实验过程中不更换研磨垫，同时设置2组对照重复实验．

通过计算得到以上2组实验的单位时间研磨去除体积，为了便于观察，将进给速度转化为研磨30mm长线段的研磨时长，同时，为了研究加工参数对表面粗糙度的影响，测量各组实验结果表面粗糙度，结果如图11所示．

从图11观察实验得到的单位时间的去除体积结果可以发现，单位时间去除体积与压力、转速、进给速度在一定范围内呈线性关系，表明固结磨料确定性研磨过程同样可以等效为卷积迭代的过程．因此，表面生成模型建立过程一个重要的基础就是将连续的加工过程等效为点加工过程，通过卷积运算的方法，针对不同参数，仿真预测研磨后的表面形貌．观察图11研磨后表面的粗糙度发现，当压力增大时，粗糙度值增加，而转速对粗糙度没有明显的影响，同时进给速度越小，粗糙度值越大．

表4 中心供液方式线研磨实验参数

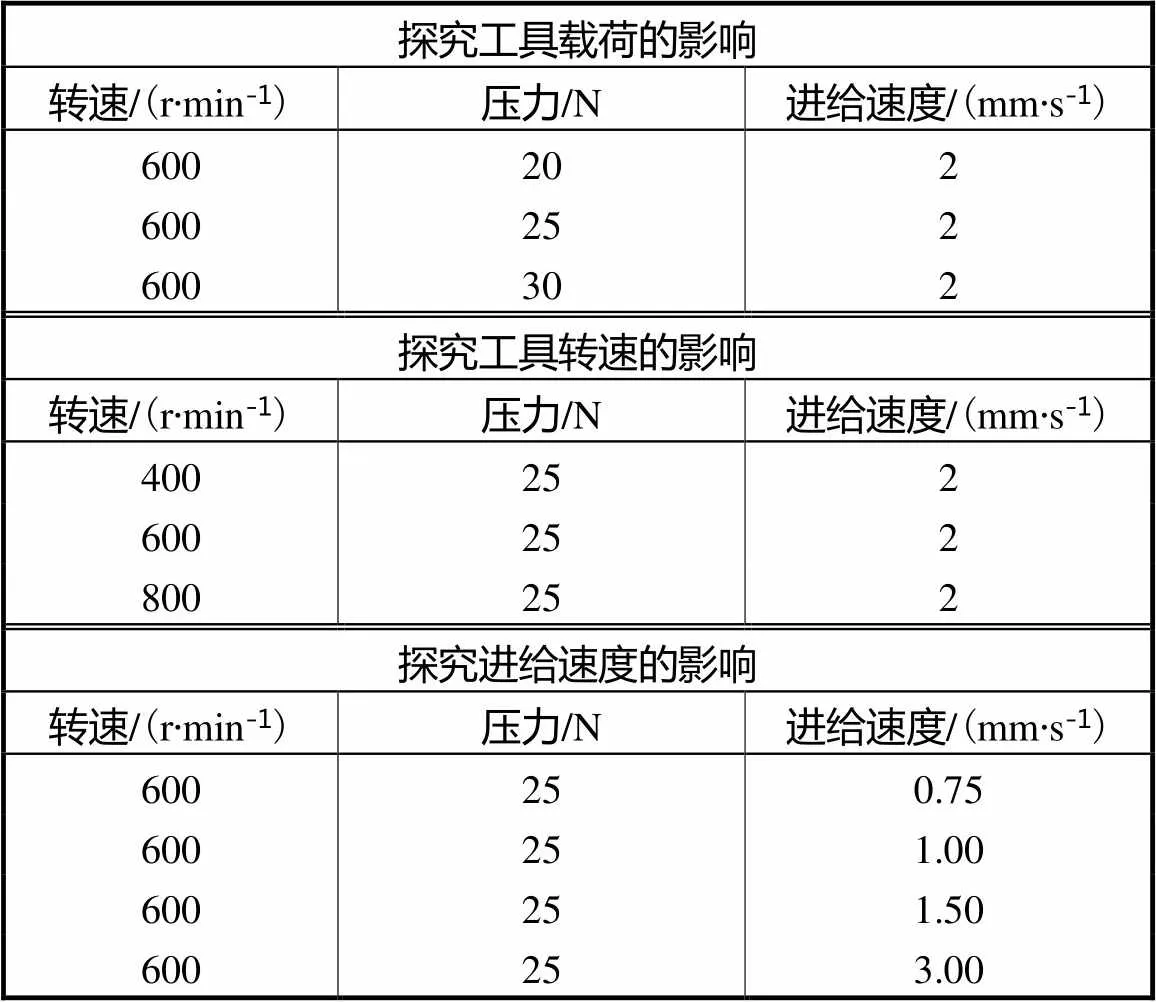
Tab.4 Line lapping experimental parameters of liquid central supply mode

图11 不同参数对去除效率及粗糙度的影响

2 确定性研磨表面生成模型建立

固结磨料确定性研磨表面生成模型总体建模流程如图12所示，可以概括为选择研磨垫及工艺参数，求解磨粒间距后对研磨垫表面进行仿真，通过采样取得采样点磨粒的出刃高度，同时根据硬脆材料去除机理求解出研磨垫和工件间的间隙，求出采样点磨粒的切入深度，继而求得单点研磨斑去除模型．将轨迹离散后，将单点研磨斑函数与轨迹函数进行卷积运算，进而仿真研磨后的表面．

图12 研磨表面生成模型建模流程

2.1 固结磨料研磨垫表面形貌仿真

固结磨料研磨垫表面形貌即研磨垫表面磨粒分布以及状态，是影响研磨过程材料去除效率、稳定性的重要因素，因此，对研磨垫表面的微观形貌进行建模是表面生成模型的基础．首先，要模拟研磨垫表面磨粒的分布以及出刃情况，再由磨粒的分布状态和出刃情况可以评定在实际加工过程中磨粒与工件的接触状况，求取不同位置磨粒切入工件的深度，建立不同参数下的单点研磨斑模型．

2.1.1 磨粒间距计算

金刚石磨粒硬度高，将其假设为刚性体，研磨液为去离子水，不含化学物质，忽略化学作用的影响． 为了简化建模过程，借鉴李军等[14]在固结磨料建模过程中提出的假设，基于微观接触机理及概率分布模型，作如下假设：①金刚石磨粒粒径均匀，形状为球形，均匀分布于研磨垫基体之中；②磨粒露出高度服从均匀分布，载荷主要由磨粒承担，不考虑研磨垫基体与工件的接触．

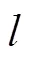
图13 磨粒晶胞模型示意

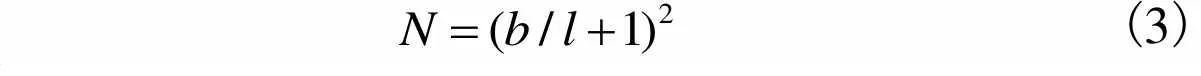
(3)

(4)

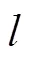
(5)

(6)

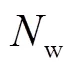
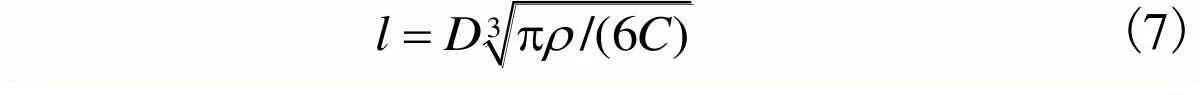
(7)

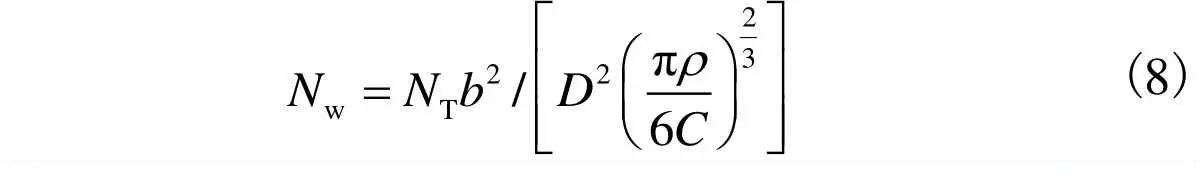
(8)

2.1.2 研磨垫微观形貌仿真

图14 研磨垫微观形貌仿真结果

2.2 单点研磨斑仿真

2.2.1 磨粒切入深度模型

(9)

接下来需要判断磨粒与工件的接触类型，如式(10)和(11)[22]所示．

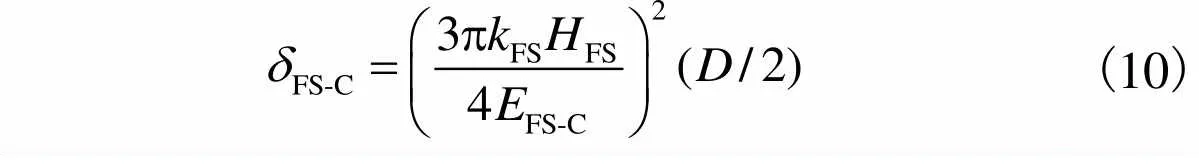
(10)

(11)

其他各个参数的值如表5所示．

表5 材料力学参数

Tab.5 Material mechanical parameters

计算得

(12)

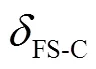
根据材料的弹性力学机理可知，金刚石磨粒与石英玻璃工件的接触力可以通过式(13)表示．

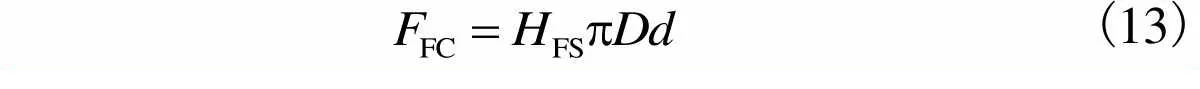
(13)

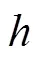
图15 研磨垫与工件微观接触示意

由图15可知，磨粒出露高度和切入深度之间的关系为

(14)

单颗磨粒的受力可表示为

(15)

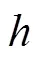
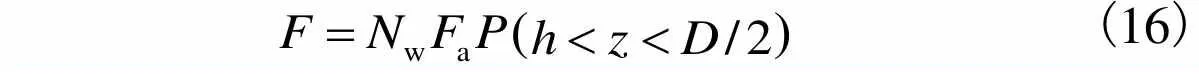
(16)

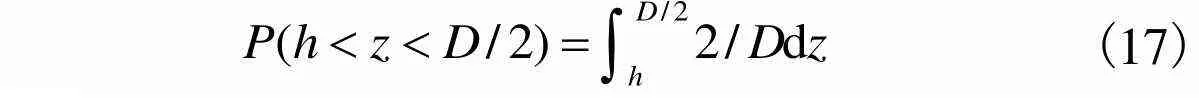
(17)

将式(15)和(17)代入式(16)得

(18)

(19)

(20)

2.2.2 单点研磨斑建模

图16 磨粒切入深度采样结果

(21)

2.3 研磨表面生成模型建立

通过MATLAB仿真，由单点研磨斑模型可得到在不同参数下单点研磨斑的数据．单点研磨斑的仿真需要构造一个包含位置信息，以及不同位置的研磨去除深度值的单点去除矩阵．矩阵的行值、列值代表了单点研磨斑的不同位置的坐标，中存储的值代表对应坐标位置的研磨去除深度．实际面加工过程是连续的，将连续的加工过程等效为离散等效点的点研磨加工的累加是一个分时合成的过程，就是把在时间上连续的加工过程等效为在时间上不连续的等效点的加工过程，通过累加在等效点处单点研磨斑而达到预测整个连续去除过程的目的，而这个累加过程就是通过去除矩阵与轨迹矩阵的卷积运算实现的．

图17 单点研磨斑径向去除深度

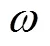
(22)

图18 轨迹离散化

Fig.18 Trajectory discretization

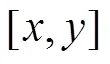
(23)

通过测量得到初始面型c，减去去除量，既可得到最终的表面f为

(24)

3 仿真与实验分析

3.1 点研磨仿真与实验分析

为了验证单点研磨斑模型对于压力、转速、时长3个参数变化引起研磨斑形状变化预测的准确性，设计并进行单点研磨斑实验．

单点实验参数见表6，其他实验条件保持不变. 进行单点研磨实验时，将小磨头工具停留在熔融石英玻璃工件表面的某一点，按照表6各组实验数据选择工具的转速及工具载荷，保持一段时间，进行定点研磨实验．

表6 单点研磨实验参数

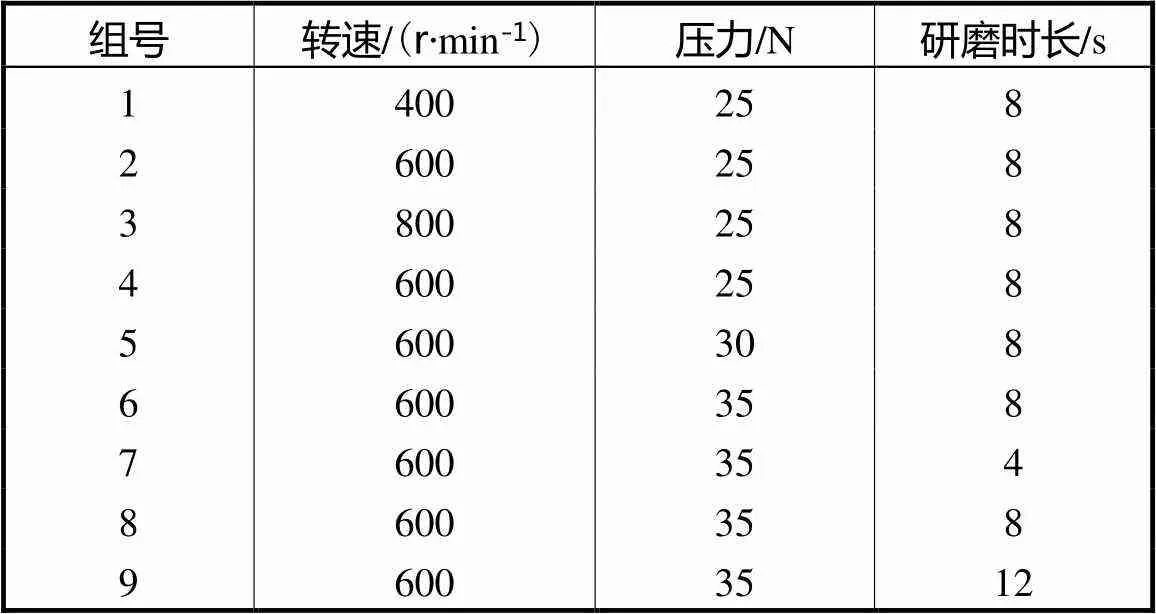
Tab.6 Point lapping experimental parameters

在进行单点研磨斑的仿真时，为了清晰、鲜明地对比实验与仿真的三维轮廓、截面轮廓，单点研磨斑仿真过程采用多项式拟合的光滑曲线．

选用Nanovea白光干涉三维轮廓仪，采用0～300μm的量程，采样步长为1μm，取第6组的实验结果，实验与仿真得到的单点研磨斑三维轮廓如图20所示．

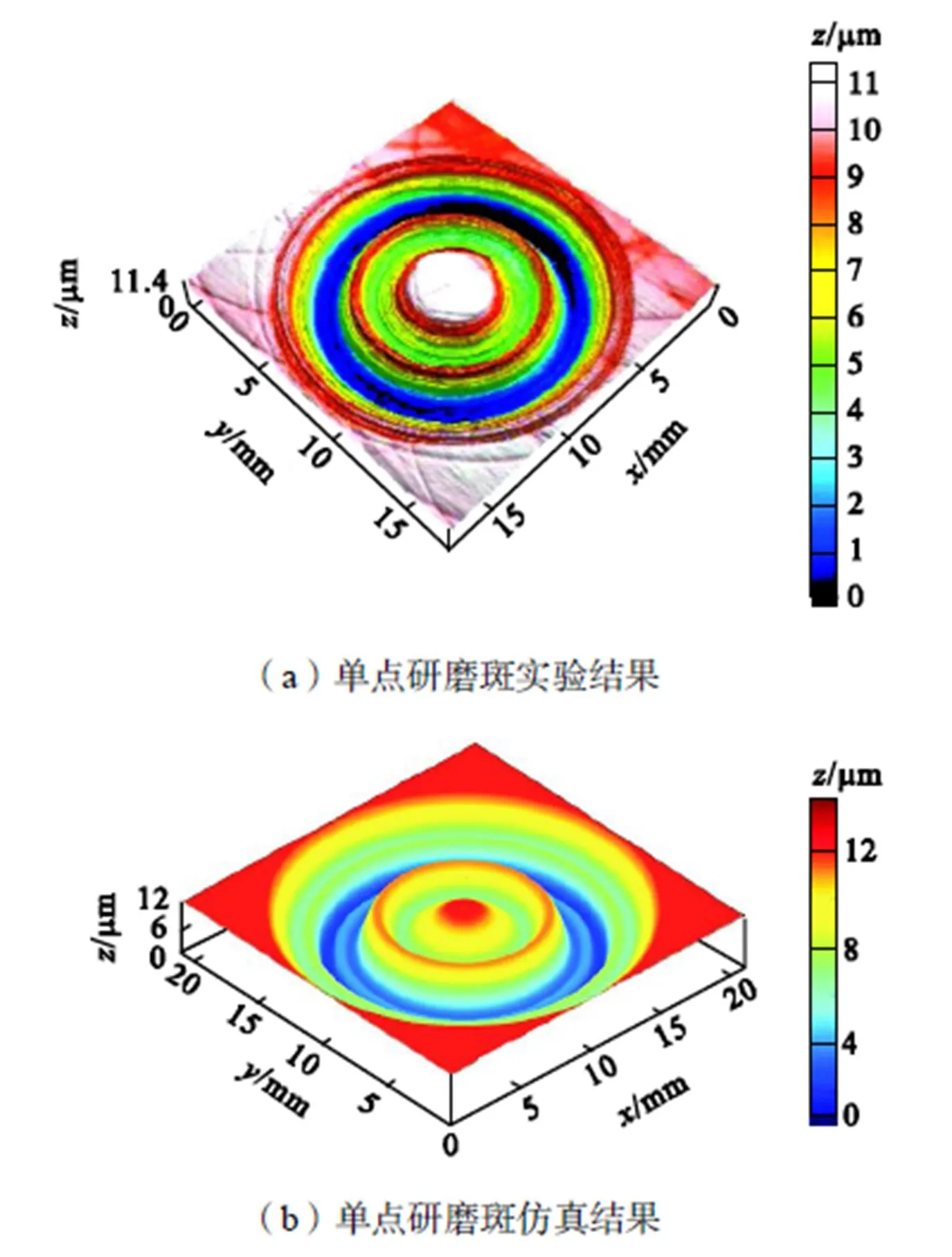
图20 单点研磨斑实验与仿真结果对比

观察图20实验与仿真得到的单点研磨斑的形貌图发现，仿真模型可以很好地模拟研磨斑径向研磨深度的变化，为了更加直观对比仿真模型的准确性，过单点研磨斑中心位置，取垂直于加工平面的截面的轮廓，分别对比不同转速、压力、时长的单点研磨斑仿真与实验截面轮廓，如图21～图23所示．

观察图21～图23的(a)～(c)实验与仿真结果的单点研磨斑截面轮廓发现，通过仿真可以很好地拟合单点研磨斑的形状．观察图21(d)和图22(d)的实验与仿真的结果发现最大去除深度一致性高，而观察图23(d)的实验结果发现，随着研磨时长的增加，仿真得到的最大去除深度渐渐大于实验得到的数据，原因可能是在进行不同研磨时长实验时，选择的压力较大，随着研磨时长的增加，磨粒脱落速度过快，实际参与去除的有效磨料的数量少于仿真模拟值，最终导致研磨时长为12s时实验与仿真结果差异较大．另一方面，研磨垫基体材料的硬度较大、难变形，随着去除深度的不断增大，压力分布越来越不均匀，与去除深度较小的区域相接触的研磨垫承受的力变大，与去除深度较大的区域相接触的研磨垫承受的力较小，因此磨粒切入深度变小，实验与仿真数据差别变大．综合来讲，单点研磨斑仿真模型能够准确预测一定参数下的单点研磨去除斑的形状和深度．

3.2 面研磨实验与仿真分析

小磨头研磨过程中常用的加工路径为线性扫描路径(光栅轨迹)，进给速度和栅格间距是影响加工后面型的重要参数，加工后工件表面容易产生光栅形式的残留误差．接下来通过仿真与实验来验证表面生成模型的准确性，同时研究工艺参数对加工后的表面质量的影响．在固结磨料研磨表面生成的仿真过程，单点的研磨斑形状不能采用拟合曲线，因为拟合曲线相当于对径向单点研磨曲线进行了滤波，生成后的表面无法反映中高频误差的情况．

图21 转速对单点研磨斑的影响

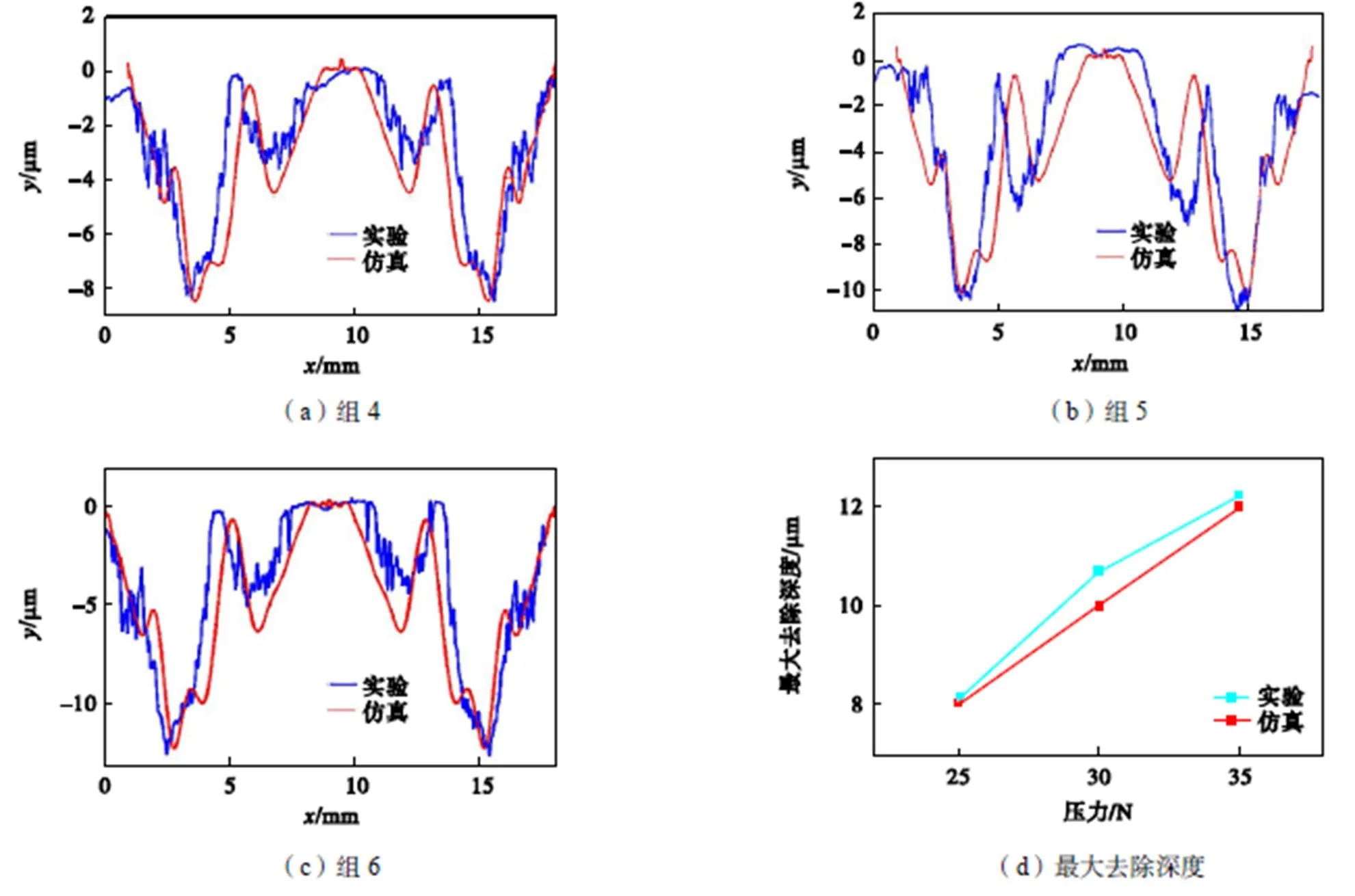
图22 压力对单点研磨斑的影响

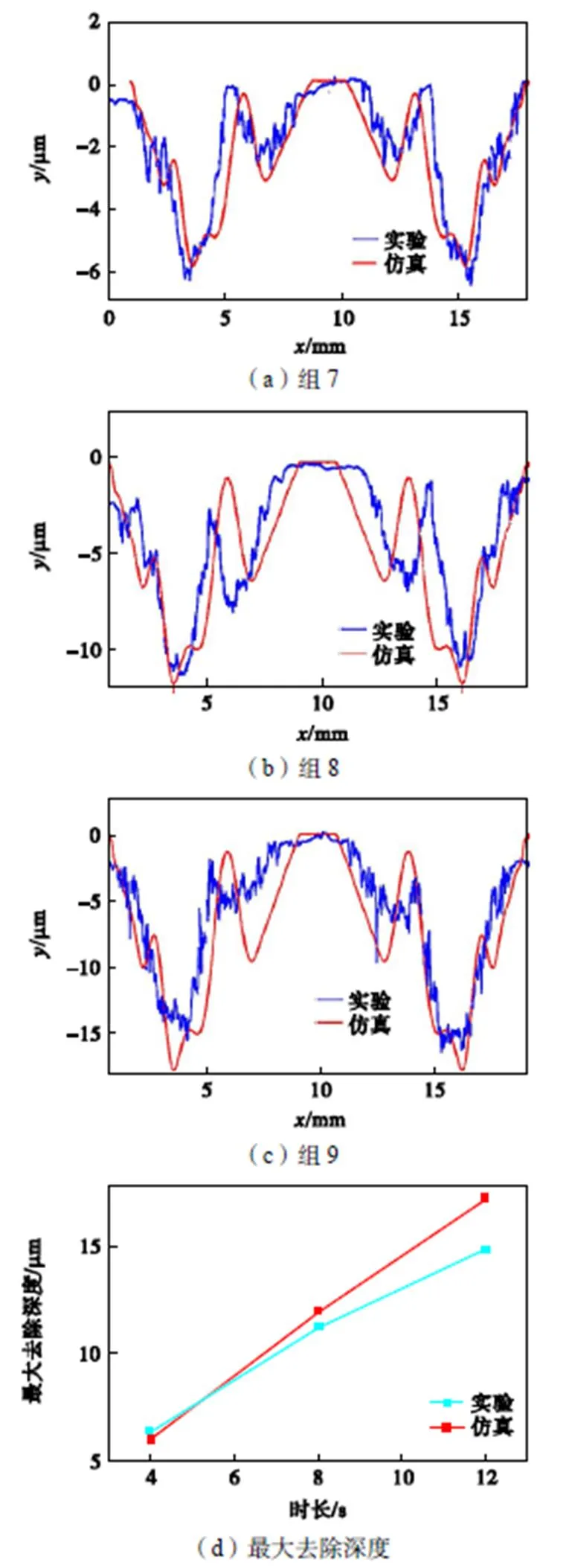
图23 时长对单点研磨斑的影响

面研磨实验工具、工件与点研磨实验情况一致，采用表7参数进行4组仿真与实验，栅格轨迹范围为30.0mm×30.0mm的方形区域．进行面研磨实验时，为保证研磨垫上磨粒能够及时更新，每隔1min对研磨垫进行修整．

通过仿真可以模拟加工后工件的面型，以组1参数为例，通过Matlab仿真绘制出研磨加工后表面的三维图如图24所示．

表7 面研磨实验参数

Tab.7 Plane lapping experiment parameters

测量各组如图24所示中心10.0mm×10.0mm区域实验结果的微观形貌，对比实验与仿真结果如图25所示．

图24 表面形貌仿真三维图(组1)

通过直观观察实验和仿真表面形貌可以发现，仿真结果很好地模拟了研磨后表面的栅格形式的残留误差．在中心区域10.0mm×10.0mm的范围内，当栅格间距为2.0mm时有5个残留误差峰，当栅格间距为3.0mm时有3个残留误差峰．

为了量化分析仿真表面对残留误差预测的准确性，取各组实验与仿真的中心区域垂直于栅格误差带方向10.0mm的直线，对比各组实验与仿真结果，如图26所示，计算各组轮廓的最大峰谷高度值即PV值，对比仿真与实验结果如图27所示．

图26 残留误差轮廓

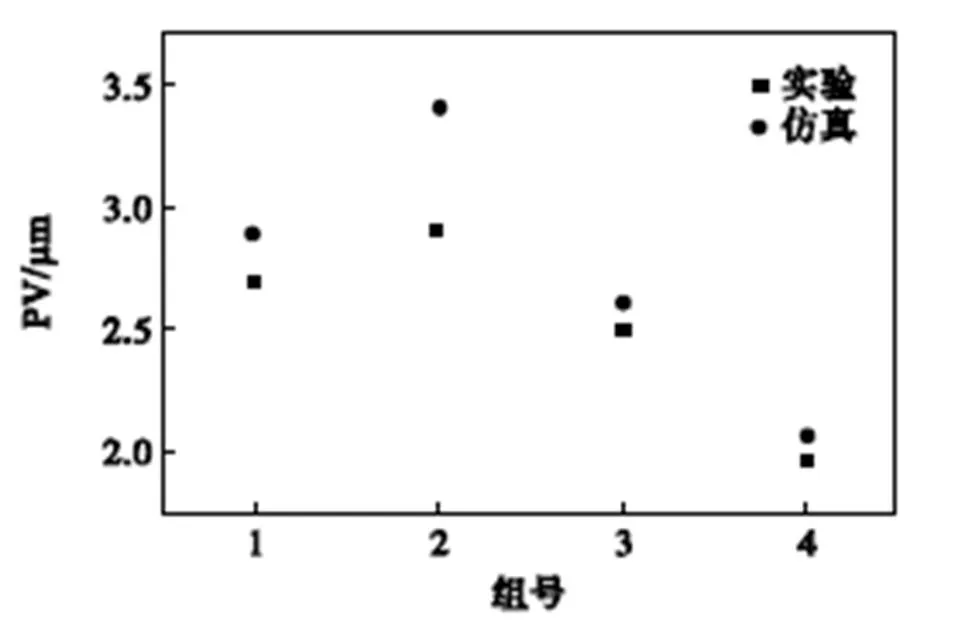
图27 残留误差轮廓PV值对比

通过图26和图27发现，当峰值较小时，例如组1、3、4的PV值，仿真结果更加准确，而当峰值较大时，模型预测的准确性较差，例如组2结果．这是因为使用的研磨垫为硬质基体，硬度较高、变形小，在实际加工过程中，当加工形成峰或谷时，由于研磨垫变形微小，接触不均匀，使局部压力增加，峰、谷区域趋于平坦，而仿真过程模拟的是柔性研磨垫的去除过程，假设研磨垫是随着面型改变而发生变形，与工件均匀接触的连续研磨加工过程，因而组2的实验结果与仿真结果偏差较大．总体而言，表面生成模型能够准确预测一定参数下栅格轨迹研磨后表面的残留 误差．

在固结磨料确定性研磨工艺中，加工区域的去除深度也是值得关注的对象，有效控制研磨深度有利于降低材料成本．测量各组实验与仿真结果平行于如图24所示方向的50.0mm的轮廓线，以组1为例，对比仿真与实验结果如图28所示．计算中心10.0mm区域的平均去除深度，与仿真对比如图29所示．

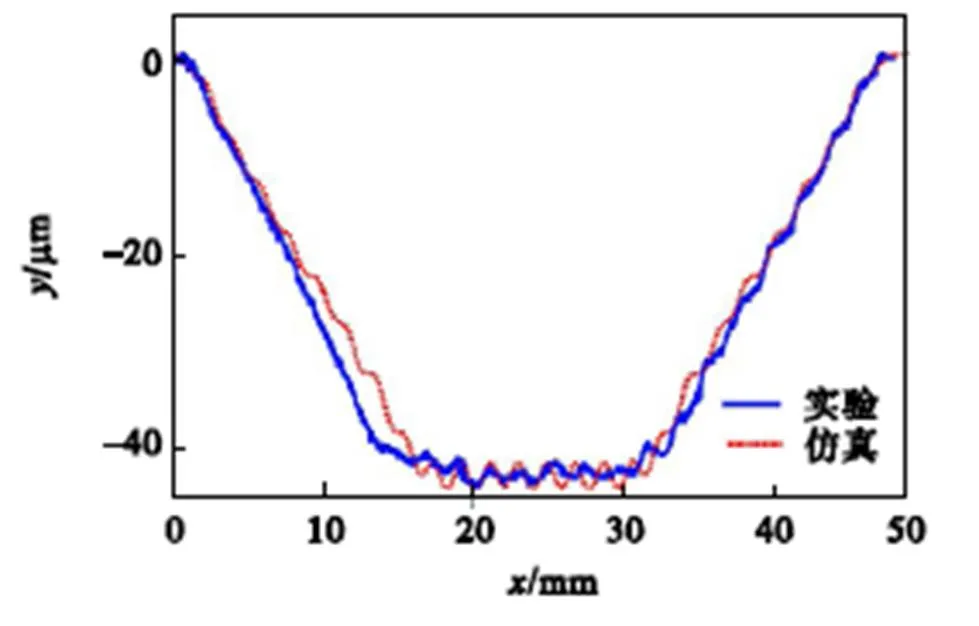
图28 表面去除轮廓(组1)

图29 中心区域平均去除深度

观察图28和图29结果发现，实验与仿真得到的表面的研磨去除轮廓与去除深度一致性高，仿真得到的数据整体略高于实验，原因是仿真求取去除深度值时假设初始表面为平面，因此造成了一定偏差．通过对去除深度值的预测，可以通过改变参数准确控制表面研磨深度，节约材料成本，去除初始表面损伤层．

4 结 论

(1) 本文借鉴CCOS技术的原理和工艺过程，提出高效、可控性高的固结磨料确定性研磨工艺，开展不同供液方式下的线研磨实验，对比表面粗糙度及材料去除效率，分析工艺参数对加工前后表面硬度影响及材料去除方式，发现中心供液方式有利于提高加工效率和表面质量．开展不同压力、转速、研磨时间的线研磨实验，发现各个参数的线性变化引起材料去除量的变化呈线性关系，表明固结磨料研磨工艺过程材料去除过程符合CCOS的卷积效应．

(2) 基于硬脆材料去除机理以及研磨垫与工件微观接触模型，借鉴晶胞理论，考虑磨粒浓度、粒度、研磨垫形状建立了研磨垫表面形貌的仿真模型．推导了研磨垫与工件的间隙求解模型，建立了单点研磨斑模型．考虑研磨垫形状、磨粒的粒径和浓度、研磨工具的转速和承受的载荷、工具轨迹参数建立了总去除量与单点研磨去除量的卷积运算关系，并提出固结磨料研磨表面生成模型．

(3) 通过不同压力、转速、时长的单点研磨实验验证了单点研磨斑模型的准确性．针对不同工艺参数进行了面研磨实验和仿真，并通过对比两者所得到表面的残留误差PV值、研磨深度证明了表面生成模型的准确性．本文的研究结果对提高研磨工艺可控性及表面质量具有一定的指导意义和参考价值．

［1］ Cho B J，Kim H M，Manivannan R，et al. On the mechanism of material removal by fixed abrasive lapping of various glass substrates[J]. Wear，2013，302(1/2)：1334-1339.

［2］ Fang C，Zhao Z，Lu L，et al. Influence of fixed abrasive configuration on the polishing process of silicon wafers[J]. International Journal of Advanced Manufacturing Technology，2016，88(1)：1-10.

［3］ Dong Z，Cheng H. Study on removal mechanism and removal characters for SiC and fused silica by fixed abrasive diamond pellets[J]. International Journal of Machine Tools & Manufacture，2014，85(5)：1-13.

［4］ Hu Z，Fang C，Deng W，et al. Speed ratio optimization for ceramic lapping with fixed diamond pellets[J]. International Journal of Advanced Manufacturing Technology，2016，90(9/10/11/12)：1-11.

［5］ Wang Z K，Wang Z K，Zhu Y W，et al. Effect of lapping slurry on critical cutting depth of spinel[J]. Applied Surface Science，2015，347：849-855.

［6］ Fang C，Yan Z，Hu Z，et al. Pattern design of fixed abrasive pads inspired by the bee colony theory[J]. International Journal of Advanced Manufacturing Technology，2018，97：2563-2574.

［7］ 郭东明，康仁科，苏建修，等. 超大规模集成电路制造中硅片平坦化技术的未来发展[J]. 机械工程学报，2003，39(10)：100-105.

Guo Dongming，Kang Renke，Su Jianxiu，et a1. Future development on wafer planatization technology in ULSI fabrication[J]. Chinese Journal of Mechanical Engineer，2003，39(10)：100-105(in Chinese).

［8］ Gobena F T，Fletcher T D，Romero V D. Diamond fixed abrasive lapping of brittle substrates[J]. Industrial Diamond Review，2004，65(1)：1-3.

［9］ 朱永伟，王 军，李 军，等. 固结磨料抛光垫抛光硅片的探索研究[J]. 中国机械工程，2009，20(6)：723-727.

Zhu Yongwei，Wang Jun，Li Jun，et al. Research on the polishing of silicon wafer by fixed abrasive pad[J]. China Mechanical Engineering，2009，20(6)：723-727(in Chinese).

［10］ 李 标，李 军，高 平，等. 游离磨料和固结磨料研磨后亚表面裂纹层深度研究[J]. 中国机械工程，2013，24(7)：895-898.

Li Biao，Li Jun，Gao Ping，et al. Study on depth of subsurface crack layer by free and fixed abrasive lapping[J]. China Mechanical Engineering，2013，24(7)：895-898(in Chinese).

［11］ Murray J. ICF quarterly report[J]. Office of Scientific & Technical Information Technical Reports，1997，7(3)：1-132.

［12］ Agarwal S，Rao P V. Modeling and prediction of surface roughness in ceramic grinding[J]. International Journal of Machine Tools & Manufacture，2010，50(12)：1065-1076.

［13］ Sun J，Chen P，Qin F，et al. Modelling and experimental study of roughness in silicon wafer self-rotating grinding[J]. Precision Engineering，2018，51：625-637.

［14］ 李 军，王慧敏，王文泽，等. 固结磨料研磨K9玻璃表面粗糙度模型[J]. 机械工程学报，2015，51(21)：199-205.

Li Jun，Wang Huimin，Wang Wenze，et al. Model of surface roughness in fixed abrasive lapping of K9 glass[J]. Journal of Mechanical Engineering，2015，51(21)：199-205(in Chinese).

［15］ Wang X，Zhang X. Theoretical study on removal rate and surface roughness in grinding a RB-SiC mirror with a fixed abrasive[J]. Applied Optics，2009，48(5)：904-910.

［16］ Uhlmann E，Ardelta T，Spurb G. Influence of kinematics on the face grinding process on lapping machines[J]. CIRP Annals-Manufacturing Technology，1999，48(1)：281-284.

［17］ Wang Y，Fu Z，Dong Y，et al. Research on surface generating model in ultrasonic vibration-assisted grinding[J]. International Journal of Advanced Manufacturing Technology，2018，96(1)：1-8.

［18］ Zhao Y J，Li H N，Zhu L D，et al. Machined brittle material surface in grinding：Modeling，experimental validation，and image-processing-based surface analysis[J]. International Journal of Advanced Manufacturing Technology，2017，93(4)：1-20.

［19］ Jones R A. Optimization of computer controlled polishing[J]. Applied Optics，1977，16(1)：218-224.

［20］ Chen X，Rowe W B. Analysis and simulation of the grinding process. Part I：Generation of the grinding wheel surface[J]. International Journal of Machine Tools & Manufacture，1996，36(8)：871-882.

［21］ Liu P，Lin B，Yan S，et al. Numerical simulation and experimental validation of fixed abrasive grinding pad topography[J]. International Journal of Advanced Manufacturing Technology，2015，83(5/6/7/8)：1-12.

［22］ Zhao Yongwu，Marietta D M，Chang L. Closure to “discussion of‘an asperity microcontact model incorporating the transition from elastic deformation to fully plastic flow’”[J]. ASME Journal of Tribology，2000，122(2)：479.

Surface Generation Modeling and Experimental Analysis of the Fixed Abrasive Deterministic Lapping Process

Lin Bin1,2，Li Kailong1,2， Cao Zhongchen1,2，Jiang Xiangmin1,2，Huang Tian2

(1. Key Laboratory of Advanced Ceramics and Machining Technology of Ministry of Education，Tianjin University，Tianjin 300350，China；2. School of Mechanical Engineering，Tianjin University，Tianjin 300350，China)

A highly efficient，controllable fixed abrasive deterministic lapping process based on the CCOS principle was proposed. Through the line lapping experiments，results indicate that the liquid central supply mode is beneficial to the improvement of process efficiency and surface quality compared with the traditional liquid supply mode. The influence of process parameters on the surface hardness after processing and the material removal mechanism of the fixed abrasive lapping was analyzed by scanning electron microscopy，in order to observe the surface topography of the workpiece after lapping. The linear relationships between the material removal rate and tool speed，load，time were verified by line lapping experiments with different parameters. Results reveal that the material removal process of the fixed abrasive lapping process conforms to the convolution iteration principle of CCOS. A simulation model of the surface topography of the fixed abrasive lapping pad was established based on the unit cell theory and the assumption of uniform abrasive particle size. At the same time，the effect of parameters，such as the size and concentration of the abrasive particles and the shape of the lapping pad，were considered in the model. Based on the simulation data of fixed abrasive lapping pad topography，the calculation model of the contact gap between the lapping pad and the workpiece was established based on the removal mechanism of the hard and brittle material and the micro-contact model between the lapping pad and the workpiece. This process also considered the mechanical properties of the workpiece surface under certain parameters. Furthermore，the point lapping removal spot model was established. The accuracy rates of this model under different pressures，rotation speeds，durations were verified by point lapping experiments. After dispersing continuous machining trajectories，the convolution operation relationship between the total lapping removal and the point lapping removal was established by considering the shape of the lapping pad，the size and concentration of the abrasive particles，the rotational speed and the load of the lapping tool，and the trajectory parameters. The fixed abrasive lapping surface generation model was also proposed. Plane lapping experiments and surface simulations with different parameters were carried out. Results show that the fixed abrasive deterministic lapping surface generation model can predict the lapping removal depth and the residual error of the lapping surface under different parameters. The proposed model can also improve the controllability of the fixed abrasive lapping process.

fixed abrasive lapping；process parameters；surface generation model；trajectory

the National Science and Technology Major Project of the Ministry of Science and Technology of China(No. 2017ZX04022001-206)，the Key Program of the Natural Science Foundation of Tianjin，China(No.18JCZDJC38900).

TG58；TG74

A

0493-2137(2019)09-0917-15

2018-09-07；

2018-10-11.

林 彬（1963—），男，硕士，研究员.

林 彬，tdlinbin@126.com.

国家科技重大专项项目(2017ZX04022001-206)；天津市自然科学基金重点资助项目(18JCZDJC38900).

10.11784/tdxbz201809015

(责任编辑：金顺爱)