层状软声子晶体带隙及传输特性的主动调控

(浙江工业大学 机械工程学院，浙江 杭州 310014)

当弹性波或声波在一些周期性复合介质中传播时，由于受周期性的Bragg散射和单散射体的Mie散射的联合作用，会形成弹性波或声波禁带，通常把此类人工合成的功能材料称为声子晶体[1-2]。基于固体能带理论，当波通过有限周期结构时，弹性波或声波在声子晶体带隙范围内能量会迅速呈指数衰减，因此声子晶体在滤波、隔震降噪等领域有着广泛的应用前景。对于此类材料带隙形成机理、分布特性以及相应的计算方法、实验测试等相关方面的研究也获得了国内外研究者极大的关注。声子晶体带隙结构主要由周期性材料的材料参数(弹性模量、剪切模量和密度等)、原胞周期性排列方式和组元材料的体积分数等因素决定。通过理论计算后选取合适的参数搭配，往往可以设计出满足特定要求的带隙结构。然而通常情况下，一旦声子晶体的材料参数与结构参数确定之后，其能带结构也就确定了，如果能够根据需要实现声子晶体带隙结构的动态调节，将为声子晶体的实际应用提供更为广阔的空间。

一维声子晶体由于构造相对简单，制备方便，在新型减震降噪设备、消音器和滤波器等制作方面已有所应用。研究者从实验、模拟和理论三个方面入手，已对一维声子晶体开展了大量的工作，并取得一定研究成果[3-7]。其中邱学云等[4]对比了一维三组元杆状声子晶体和一维二组元杆状声子晶体的带隙特征以及传输性质，研究发现三组元声子晶体的带隙比二组元声子晶体的带隙更宽，带隙中心频率更低。贾晓珍等[8]在一维层状声子晶体的传播特性的研究中也得到了类似的结论。由此可见一维三组元声子晶体相比于二组元声子晶体在实际应用中更具有优势。目前对一维三组元声子晶体的研究大多停留在带隙的被动调控层面，很少有人尝试研究带隙的主动调控。近年来随着材料科学的发展，新型功能材料在声子晶体中的应用为这一目标的实现提供了一条新的途径。超弹性材料作为一类软材料在受到外力作用下能够发生非常大的变形，与此同时材料自身的力学属性也会发生显著改变，而这正是影响声子晶体带隙结构的重要因素。因此与传统硬材料相比，超弹性材料在可调控声子晶体中的应用具有非常明显的优势，通过施加不同的机械力偏场可以实现声子晶体的带隙结构的主动调控。国外Bertodli课题组[9-12]利用多孔超弹性材料微观结构力致失稳的机理，通过外加荷载来改变多孔声子晶体的拓扑结构，实现了声子晶体带隙结构的动态控制。Huang等[13]报道了静态力偏场对于可压缩一维声子晶体中小幅值纵波禁带结构的调控作用，并且研究了材料组分比对带隙宽度、位置的影响。笔者以超弹性材料构成的三组元层状软声子晶体为研究对象，首先基于非线性有限变形理论[14]，计算了不同预应力偏场作用下三组元层状软声子晶体各组分材料参数、几何尺寸的变化，然后通过有限元软件Comsol建模研究了结构中小幅值纵波传播问题，分析了预应力偏场对于声子晶体带隙分布以及有限周期层合结构中传输特性的影响。

1 模型及理论

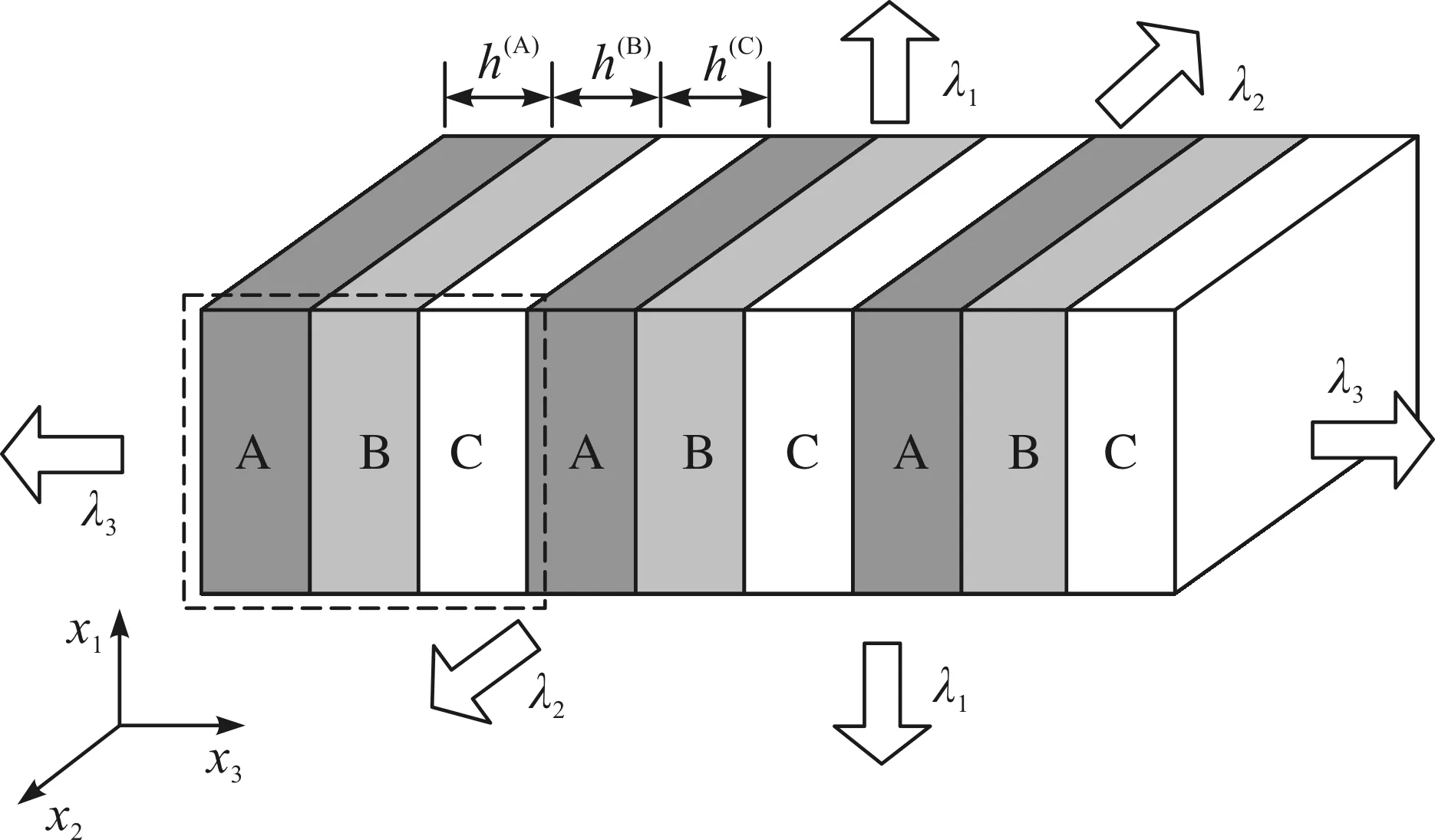
图1 两端预拉伸超弹性材料声子晶体示意图Fig.1 Schematic illustration of the periodic hyperelastic laminates

根据非线性大变形理论[14]，对于可压缩超弹性材料，取物体未变形时的初始构型为参考构型，其上的点记作X，经过运动x=χ(X,t)，初始构型变为现时构形。其中X和x分别表示初始构型以及现时构形的位置向量。笔者采用可压缩的neo-Hookean能量密度函数[15]来描述超弹性材料，即

(1)

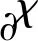
Jτ=2Ω1b+2I3Ω3I

(2)

式中：b=FFT;Ωm=∂Ω/∂Im;J=detF。

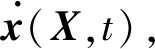
(3)

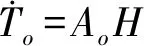
(4)

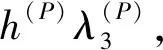
(5)

式中

(6)

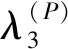
(7)

2 数值仿真与分析

数值建模所采用的材料参数见表1。

表1 超弹性材料参数表1)Table 1 Material properties

注：1)E为弹性模量；μ为剪切模量。

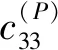
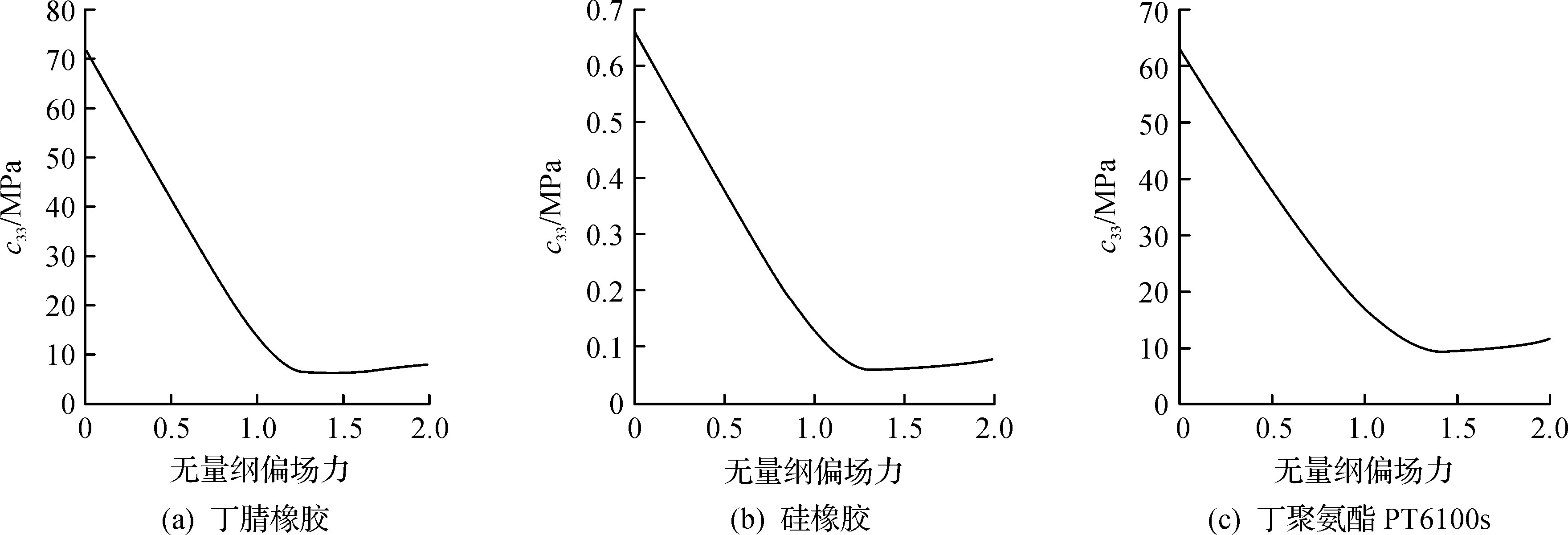
图2 三种组元材料弹性模量变化图Fig.2 Variations of and with for the composite

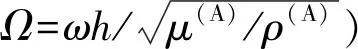
TL=log10(|p1/p0|)

(8)

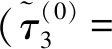
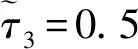
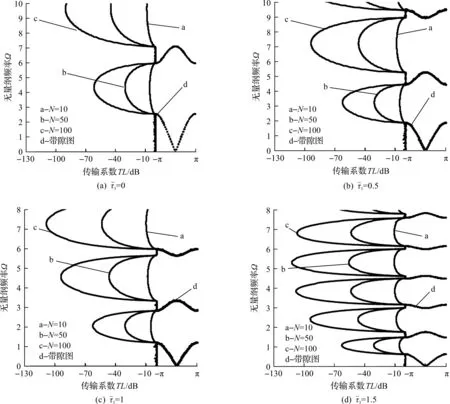
图3 一维三组元声子晶体不同力偏场下的带隙图及传输图谱(v(A)∶v(B)∶v(C)=1∶1∶1)Fig.3 Band gaps distribution and transmission spectrum as functions of for the soft laminates(v(A)∶v(B)∶v(C)=1∶1∶1)

当三种材料组分比由v(A)∶v(B)∶v(C)=1∶1∶1(变为v(A)∶v(B)∶v(C)=1∶2∶2时，对比图3，4可以看出带隙位置降低了，这是由于原胞中等效模量较小的硅橡胶组分比增加，结构整体刚度减小所导致。而当改变组分比为v(A)∶v(B)∶v(C)=1∶1∶3时，从图3～5的对比中可以看出：由于等效模量较大的组分材料聚氨酯比例上升，结构整体刚度明显增加，带隙位置显著提高。

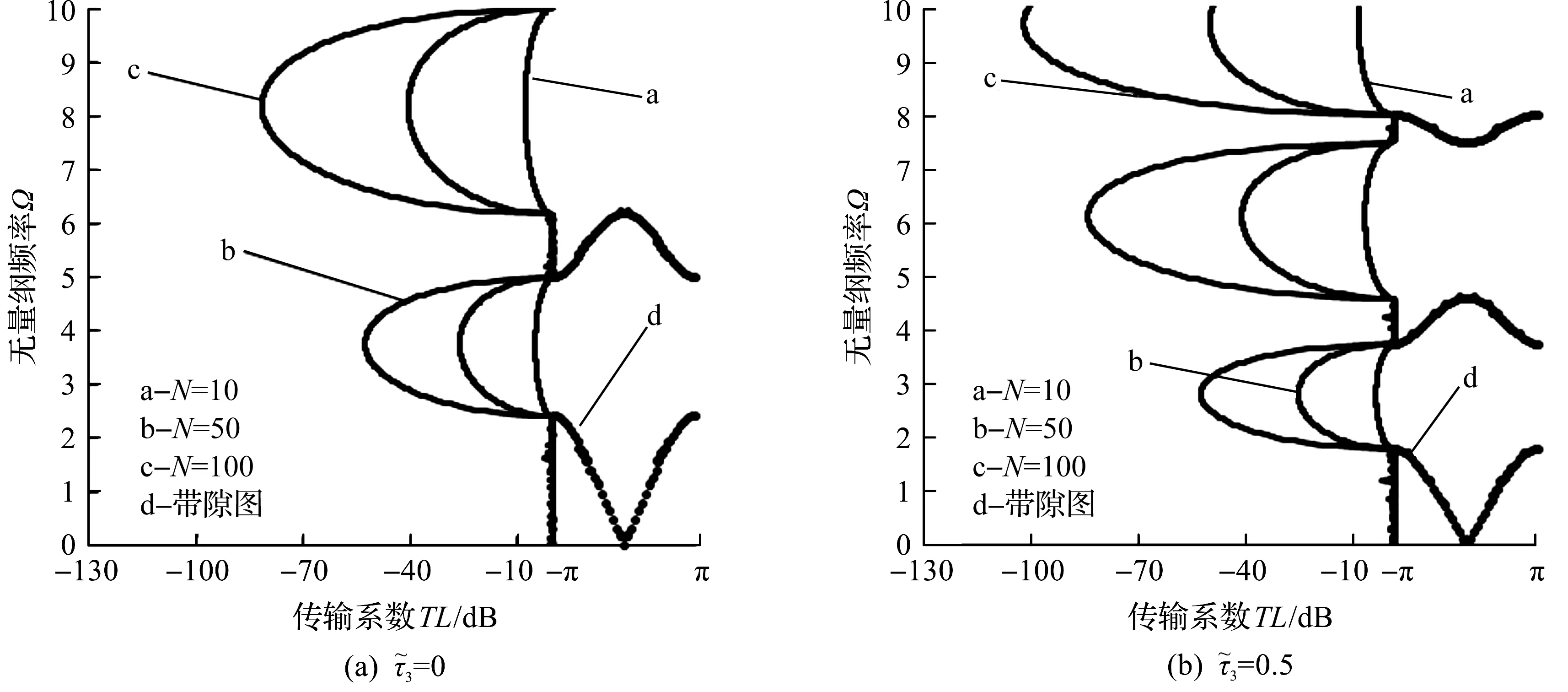
图4 一维三组元声子晶体不同力偏场下的传输图谱( v(A)∶v(B)∶v(C)=1∶2∶2)Fig.4 Band gaps distribution and transmission spectrum as functions of for the soft laminates (v(A)∶v(B)∶v(C)=1∶2∶2)

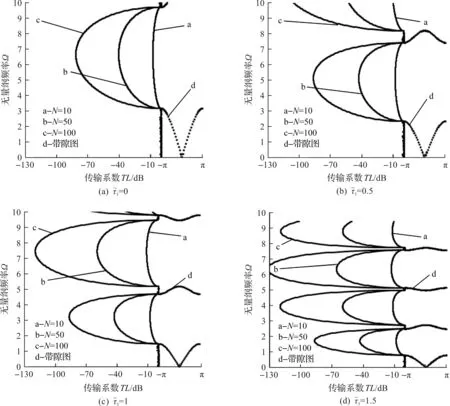
图5 一维三组元声子晶体不同力偏场下的传输图谱 v(A)∶v(B)∶v(C)=1∶1∶3Fig.5 Band gaps distribution and transmission spectrum as functions of for the soft laminates (v(A)∶v(B)∶v(C)=1∶1∶3)

3 结 论

以三种可压缩超弹性材料组成的一维三组元层状声子晶体为研究对象，采用非线性有限变形理论计算不同力偏场作用下三种组分材料参数、几何尺寸的变化，然后通过有限元软件Comsol建模研究了结构中小增量场纵波传播问题，分析了预应力偏场、材料组分比对结构带隙分布以及传输特性的影响，从理论上实现了力偏场对一维三组元超弹性声子晶体中纵波传输行为的主动调控。