机电产品模块化设计重用的博弈决策

(1.浙江工业大学 设计艺术学院，浙江 杭州 310023；2.浙江工业大学 机械工程学院，浙江 杭州 310014)

在机电产品竞争日趋激烈的国际化市场环境下，对产品提出了快速设计与制造、大批量、个性化以及低成本等要求，模块化设计正是为了满足这些要求而发展的机电产品设计方法。所谓模块化设计是指在对一定范围内的不同功能或相同功能不同性能、不同规格的产品进行功能分析的基础上，划分并设计出一系列功能模块，通过模块的选择和组合构成不同的产品，以满足市场不同需求的设计方法[1]。模块化设计过程中，模块的选择和组合方式很多，不同模块组合的产品，其功能、性能、可靠性和成本等不同，且这些指标常常是相互矛盾的，因此设计者设计产品需要综合考虑产品功能[2]、可靠性、制造和维护成本[3]等多目标要求，最终形成一个尽可能满足多个设计目标要求的方案即博弈均衡。因此如何优化模块化设计在本质上也是一个多目标优化问题。基于多目标的产品优化设计问题与博弈思想的相似性，1991年Rao等[4]率先将博弈论方法应用到机械设计的多目标优化问题中，随后国内外众多学者开展了这方面的研究，Dingra等[5]基于合作博弈理论证明了博弈论可以作为解决多目标优化问题的工具，Lewis等[6]结合飞行器中的多学科设计问题，探讨了合作、非合作和领导随从等3 种博弈模型，谢能刚等[7-8]将博弈论方法应用于拱坝体型和滑轮组变幅机构多目标优化设计，赵健冬等[9]研究了基于Nash均衡的多学科优化设计求解方法，并应用于挖掘机工作装置设计, 陈亮等[10-11]根据各博弈方策略集划分情况，分别构建基于合作博弈、非合作博弈和混合博弈等多目标设计决策模型，并探讨各种模型的求解方法，Xiao等[12]提出一种非合作环境下多目标多学科设计优化问题的新方法，方法基于博弈论的纳什均衡。

通过对多目标模块化设计重用过程的分析，发现其与博弈论思想的契合度非常高。笔者将多目标设计优化的博弈论思想发展，推广应用于模块化设计重用的决策问题，论述产品模块化设计重用博弈策略的建立方法，针对合作博弈、非合作博弈与混合博弈等3 种博弈形式，分别建立相应的数学模型和求解方法，并以小型健身器械——踏步机的模块化设计为例验证方法的有效性。

1 模块化设计重用问题

(1)

式中：X为一组由可变参数组成的n维向量，称为设计变量或设计参数；F(X)为目标函数；fi(X)为各设计需求(目标)收益函数；gi(X)，hj(X)分别称为不等式约束函数和等式约束函数；变量数n、约束个数k和l之间是相互独立的，无任何关联；s.t.(subjected to)表示“受制于”。

采用博弈论方法求解式(1)表示的模块化多目标设计重用问题，需要对已有模块进行整理，划分博弈方并建立相应的策略空间。

机电产品一般由功能模块、控制模块、动力模块和基座(机架)模块等N个模块组成。根据博弈设计重用的要求，将以上模块中的各设计变量(设计参数)按设计需求重新划分与归类，将它们划分与归类为功能参数、控制参数、动力参数、可靠性以及成本等m个设计需求，作为博弈模型中的m个博弈方P={P1,P2,…,Pm}，如图1所示。

图1 机电产品模块构成和设计需求划分Fig.1 Modular structure of electromechanical product and design requirement

(2)

(3)

2 目标函数与求解

2.1 博弈方收益函数

对于图1所示的m个博弈方(设计需求)P={P1,P2,…,Pm}中任一博弈方Pj及相应的策略空间Sj(X)，建立收益函数。建立收益函数的基本原则：1) 能够体现各设计变量在各设计需求中的重要性；2) 能够体现各模块在各设计需求中的重要性。根据这两条基本原则，可以建立的收益函数形式很多，笔者建立的收益函数为

(4)

在各博弈方收益函数式(4)的基础上，根据产品的类型与模块化设计要求等，从合作博弈、非合作博弈和混合博弈等3 种博弈类型出发，建立相应的数学模型并求解。

2.2 合作博弈

合作博弈将整体收益最佳作为决策目标，因此整体收益函数应与各博弈方收益函数正向相关。建立整体收益函数,即式(1)中的目标函数F(X)为

(5)

式中bj(0≤bj≤1)表示第j项需求对整体产品的重要性，称为需求-产品重要性指数。

合作博弈的目标函数及最后的求解结果，能较准确地体现各设计需求对产品整体的重要性，该模型适用于各设计需求对产品整体的相对重要性较为明确的产品设计。

2.3 非合作博弈

(6)

式中：Xi为第i个设计方案；M为可选的模块化设计方案总个数。根据纳什均衡，对于每一个博弈方j，其对任一设计方案的收益期望值相等，即

(7)

(8)

(9)

非合作博弈模型不能体现各设计需求对产品整体的相对重要性，故其适用于各博弈方设计需求对产品整体的相对重要性较模糊或者无法确定的产品设计。

2.4 混合博弈

在合作博弈与非合作博弈均不非常适合的情况下，可以将两者结合，采用混合博弈模型，即将关系紧密的博弈方组成博弈同盟，在同盟内部进行合作博弈，在同盟外部进行非合作博弈。

设共有m个博弈方，其中k个博弈方P1,P2,…,Pk组成一个博弈同盟，同盟内部进行合作博弈，参照合作博弈整体收益函数式(5)，博弈同盟收益函数fco(X)为

(10)

式中：fl(X)为博弈同盟中第l个博弈方的收益函数，其计算同式(4)；bl(0≤bl≤1)表示第l个博弈方需求对同盟的重要性，称为需求-同盟重要性指数。

将博弈同盟作为一方(收益函数为fco)，与不参与同盟的m-k个博弈方(收益函数为fj)组成非合作博弈，并按前述非合作博弈方法求解。这种博弈方法称为混合博弈，当博弈同盟不止一个时，同样适用。

2.5 模型的求解

由以上3 种博弈模型的分析可知：模块化设计重用的目标函数F(X)可以统一写成

(11)

式中指数wj对于不同的博弈模型，其意义有所不同，如式(5，10)所述，其中对于非合作博弈，wj=1,j=1,2,…,m。

实际产品设计过程中，不论采用何种博弈模型，其最终的最优策略应该是相近的，甚至是一致的。式(11)表示的3 种博弈模型最终目标函数的统一性正是反映了这种特性。

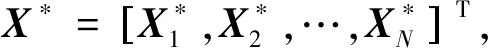
由于合作博弈体现了各设计需求对产品整体的相对重要性，而非合作博弈模型不能体现这种相对重要性(混合博弈介于二者之间)，因此，在一般情况下应优先考虑采用合作博弈模型。

3 设计简例

将以上博弈论方法用于踏步机产品的模块化设计重用。踏步机是一种小型健身器材，主要用于腿部运动健身，其主要模块包括踏板模块、运动机构模块和机架模块，如图2所示。该款机型当前可供设计重用的历史方案共有4 种，分别为方案1～方案4，它们各功能模块的相关变量如表1所示。这些历史方案的模块重组后可以组成的设计方案共有4×4×4=64 种。新的设计就是从这64 种方案中选取较为合适的参考设计方案。

图2 踏步机及功能模块Fig.2 Step machine and its functional modules

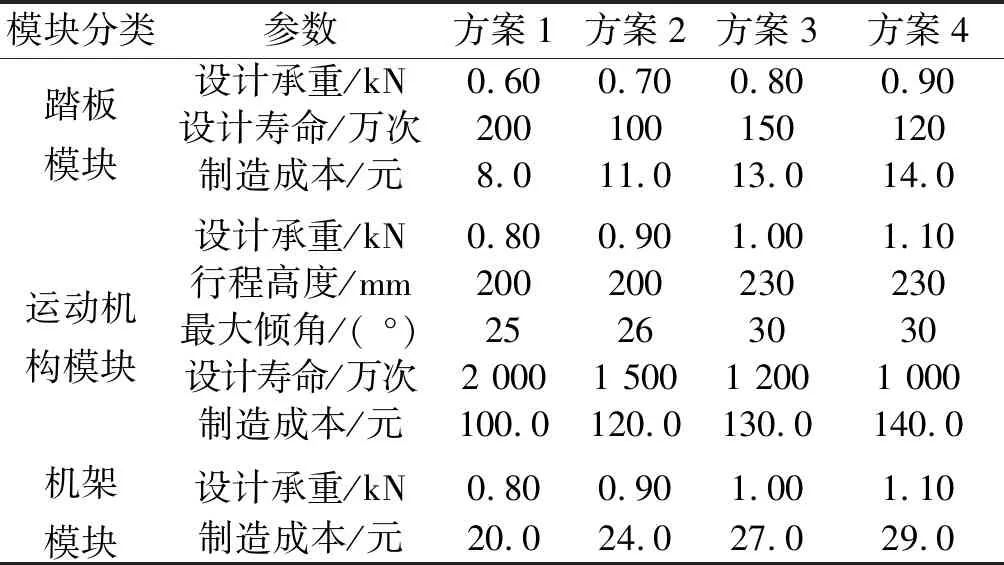
模块分类参数方案1方案2方案3方案4踏板模块设计承重/kN0.600.700.800.90设计寿命/万次200100150120制造成本/元8.011.013.014.0运动机构模块设计承重/kN0.800.901.001.10行程高度/mm200200230230最大倾角/( °)25263030设计寿命/万次2 0001 5001 2001 000制造成本/元100.0120.0130.0140.0机架模块设计承重/kN0.800.901.001.10制造成本/元20.024.027.029.0

按式(3)对表1各设计变量进行归一化处理，得到表2所示归一化设计变量。其中踏板行程高度与最大角度为有最优值的参数，最优行程高度为220 mm，最优最大角度为28°；设计承重与设计寿命为无最优值参数，为正向指标，制造成本为无最优值参数，为逆向指标。

表2 归一化设计变量Table 2 Normalized design variables

本次设计要求：利用已有模块进行重组，设计1 台踏板承重W1≥0.75 kN的新样机，其中约束条件为W3≥1.1W1。因此，方案1及方案2的踏板模块被排除出本次设计策略空间。

根据设计变量的属性，将各设计变量划分为3 类设计需求(3 个博弈方)：功能需求(设计承重、行程高度和最大角度)、制造成本需求以及可靠性需求(设计寿命)。根据踏步机的特点，设定模块-需求权重系数aij如表3所示。

表3 模块-需求权重系数aijTable 3 Module-requirement weight coefficient aij

对所有的设计方案，用编号ijk表示，其中i,j,k依次为踏板模块、运动机构模块和机架模块的选择方案编号，例如324方案表示选择方案3的踏板模块、方案2的运动机构模块以及方案4的机架模块的设计方案。将表2变量值代入式(12)，计算得到不同设计方案时各博弈方的收益函数值，列于表4。

表4 不同设计方案对应的各博弈方收益函数Table 4 Benefit of each player for different design scheme

以下分别通过合作博弈、非合作博弈和混合博弈等3 种模型进行设计求解。

1) 合作博弈：根据各博弈方需求对踏步机整体的重要性，确定需求-产品重要性系数bj为功能需求b1=1.0，成本需求b2=1.0，可靠性需求b3=0.5,代入式(5)，有

(13)

2) 非合作博弈：由式(9)可得

F(X)=f1(X)f2(X)f3(X)

(14)

3) 混合博弈：将功能需求与可靠性需求组成博弈同盟，取功能需求与可靠性需求的需求-同盟重要性指数分别为b1=0.7和b2=0.3，由式(9，5)可得

(15)

将表4所有设计方案的各博弈方收益函数分别逐一代入式(13～15)，求出各个博弈模型的各个设计方案相应的目标函数值F(Xi)，分别按其数值大小排序，取函数值最大的若干个方案作为本次设计的备选方案。本次设计结果：合作博弈和混合博弈排序前3 个设计方案完全相同，均为422，322和423，而非合作博弈排序前3 个设计方案为322,323和324。由此可见：3 种博弈方法的博弈结果是相近的，由于非合作博弈没有考虑需求-产品重要性系数，因此与另2 种博弈模型结果略有差别。该设计虽然相对简单，但在一定程度上验证了笔者所建立方法的可行性和有效性。

4 结 论

据模块化设计重用的博弈要求，将机电产品划分为功能参数、控制参数、动力参数、成本以及可靠性等设计需求，并构建相应的策略空间，划分方法具有一定的科学性和普遍性，对于模块化设计重用，完全是合适的；提出了构建各博弈方收益函数的基本原则，并构建了相应的收益函数，构建的收益函数综合考虑各个模块及各个设计变量在整个产品中的重要性，符合产品设计的基本要求；从合作博弈、非合作博弈和混合博弈等3 种博弈方式出发，分别建立了相应的设计决策模型以及统一的目标函数和求解方法。将所建立的博弈模型及求解方法用于小型健身器材的模块化设计重用，算例结果表明：求解结果基本符合实际设计情况，具有指导意义，建立的博弈模型和求解方法是可行和有效的。