基于遗传算法的永磁同步电机自抗扰控制

(浙江工业大学 机械工程学院，浙江 杭州 310014)

永磁同步电机(Permanent magnet synchronous-motor, PMSM)具有结构简单、工作效率高等特点，在工业、交通、军事和航空等重要领域得到广泛应用[1]。但永磁同步电机存在强耦合、参数易变和非线性等特点[2]，要考虑参数及负载变化对控制性能的影响。目前常用的控制策略如PID控制[3]，它是以系统的偏差进行控制，控制简单，易于实现，但是PID是采用线性方法，对于非线性系统来说，在抗扰动方面难以实现高精度的控制[4-5]。

电机运行过程中的负载、参数变化等因素[6]限制了经典PID控制方法的应用范围。如果是固定扰动，可以通过前馈环节对扰动进行补偿，但在实际应用中，扰动往往是变化的，不可测量的，对系统造成不可估计的影响，所以要对系统内外扰动进行观测，以便系统根据得到的数据及时作出调整。自抗扰控制(ADRC)不依赖于被控对象准确的数学模型[7-9]，系统内部及外部扰动由观测器观测出来并加以补偿，所以对系统参数变化和外部扰动不敏感；同时，ADRC控制器还设置了跟踪微分器和非线性状态误差反馈控制[10-14]，实现无超调快速跟踪。笔者在矢量控制与PID控制[9]的基础上采用ADRC技术对永磁同步电机进行控制。该系统可实现位置、速度和扰动的观测，用ADRC控制器代替矢量控制中的位置和速度控制器，电流环采用PI控制器。

1 问题描述

PMSM在两相同步旋转d—q坐标系下，采用id=0矢量控制策略[10-14]，电机运动方程为

(1)

ADRC的二阶控制对象为

(2)

式中：u为系统控制量；b为u的系数；f(x)为系统总扰动。

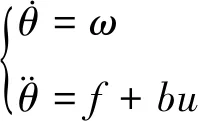
(3)

将PMSM数学模型转化为

(4)

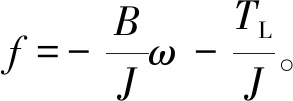
2 PMSM的ADRC位置控制器设计

ADRC由3 部分组成：安排过渡过程、扩张状态观测器和非线性组合[7]，结构框图如图1所示。

图1 二阶自抗扰控制器结构框图Fig.1 Structure block diagram of two order auto disturbance rejection controller

在对系统状态进行观测之前，需要设计一个微分器来实现过渡，使系统可以无超调跟踪，微分器采取近似微分的方法来实现。

跟踪微分器(TD)形式为

(5)

式中：h为采样周期；e0为位置跟踪误差；r为可调系数，r越大上升越快。fst函数为

(6)

其中

(7)

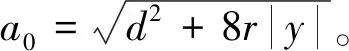
扩张状态观测器(ESO)[6]是整个自抗扰控制系统的关键部分，它能观测系统状态和扰动，实时反馈给系统进行补偿，其表达式为

(8)

其中

式中：z1，z2，z3分别为位置θ，速度ω还有总扰动f的估计值。

补偿后系统控制量为

(9)

为了克服系统扰动，提高系统鲁棒性，自抗扰控制器的非线性组合采用基于模型的PI鲁棒控制[15]。

由前面所述，永磁同步电机伺服系统描述为

(10)

位置跟踪误差为e1=θ-z1，速度跟踪误差为e2=ω-z2，定义误差函数为e=e2+5e1，定义x=e+z2，则有

(11)

控制率设计为

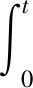
(12)

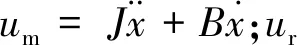
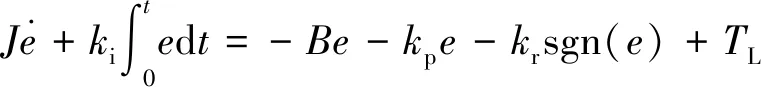
(13)

其中

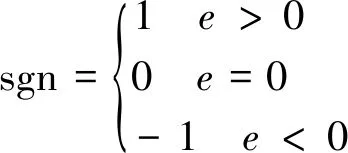
下面进行稳定性分析，取Lyapunov函数为

(14)

对V进行求导，并将式(13)代入，可得

(15)

基于矢量控制[8]的PMSM自抗扰位置控制器系统框图如图2所示。

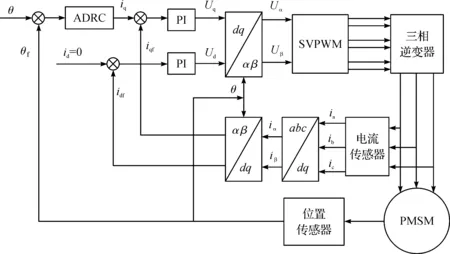
图2 ADRC位置控制器系统框图Fig.2 Block diagram of ADRC position controller system

3 基于遗传算法的ADRC参数优化

上述ADRC控制器待优化的参数有ESO的β1，β2，β3，考虑系统整体稳定性的要求，观测器的观测值应该尽可能接近系统的实际状态，所以，遗传算法的目的是使观测的位置和总体扰动误差尽可能低。将遗传算法适应度函数选择为位置误差及总和扰动误差的平方根值，设计适应度函数为

(16)

式中：N为种群个体数，这里N=50；w1，w2为权重，w1=0.7，w2=0.3。

1) 参数编码：将待优化的参数β1，β2，β3作为个体的3 个基因进行编码[16]。随机产生个体数为50的初始种群Ai(i=1，2，…，50)，初始种群是参数假设解的集合，最优参数从这些初始种群出发，经过一系列遗传算法优化求出。种群的搜索范围为β1∈[0,200]，β2∈[0,800]，β3∈[0,1 800]。

2) 选择：选择的目的是将有用的遗传信息保留下来，提高收敛速度。个体选择采用最佳保留选择，即将轮盘赌方法选择的当前群体中使适应度函数小的群体[17]，遗传到下一代群体中。

3) 交叉和变异：交叉即按照概率Pc选择2 个基因进行同位置的染色体互换；变异即按照概率pm对基因某些位进行取反[18-19]，即0变1，1变0。交叉概率Pc和变异概率Pm的选择按照自适应调整的方法进行，这样可以避免固定的交叉变异概率值对环境的不适应，2 个值分别进行适应度调节，即

(17)

(18)

式中：fmax为适应度最大值；favg为每代适应度均值；f为两个交叉个体中适应度最大值；f*为变异个体的适应度值。

4) 全局最优收敛：当遗传代数达到设定值或者适应度值不再剧烈变化时，则算法结束，全局收敛，否则返回2)循环执行。最终得到优化后的参数值为β1=103.95，β2=398.57，β3=1 132.26。

遗传算法流程图及优化框图分别如图3，4所示。

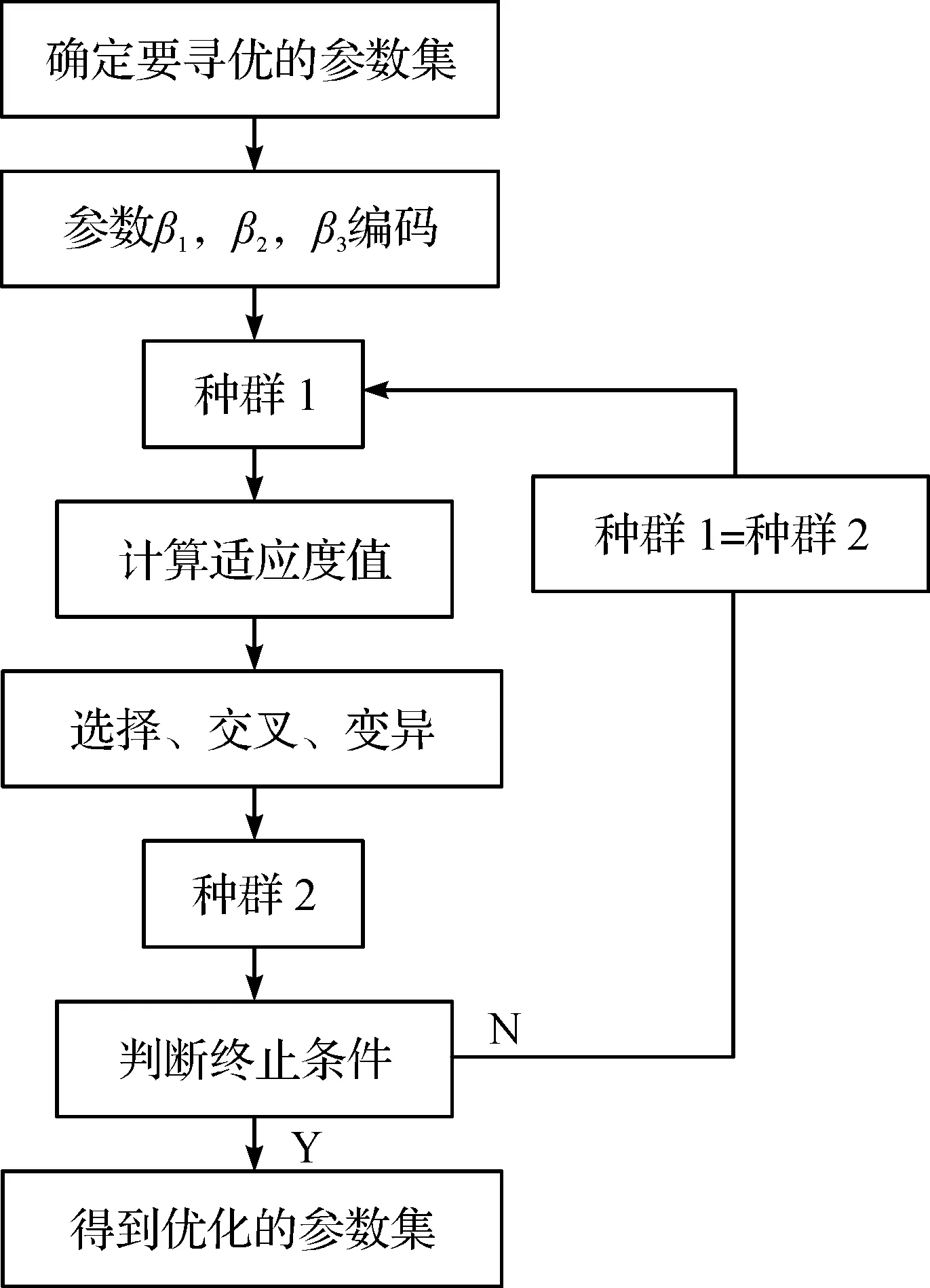
图3 遗传算法流程图Fig.3 Flowchart of genetic algorithm

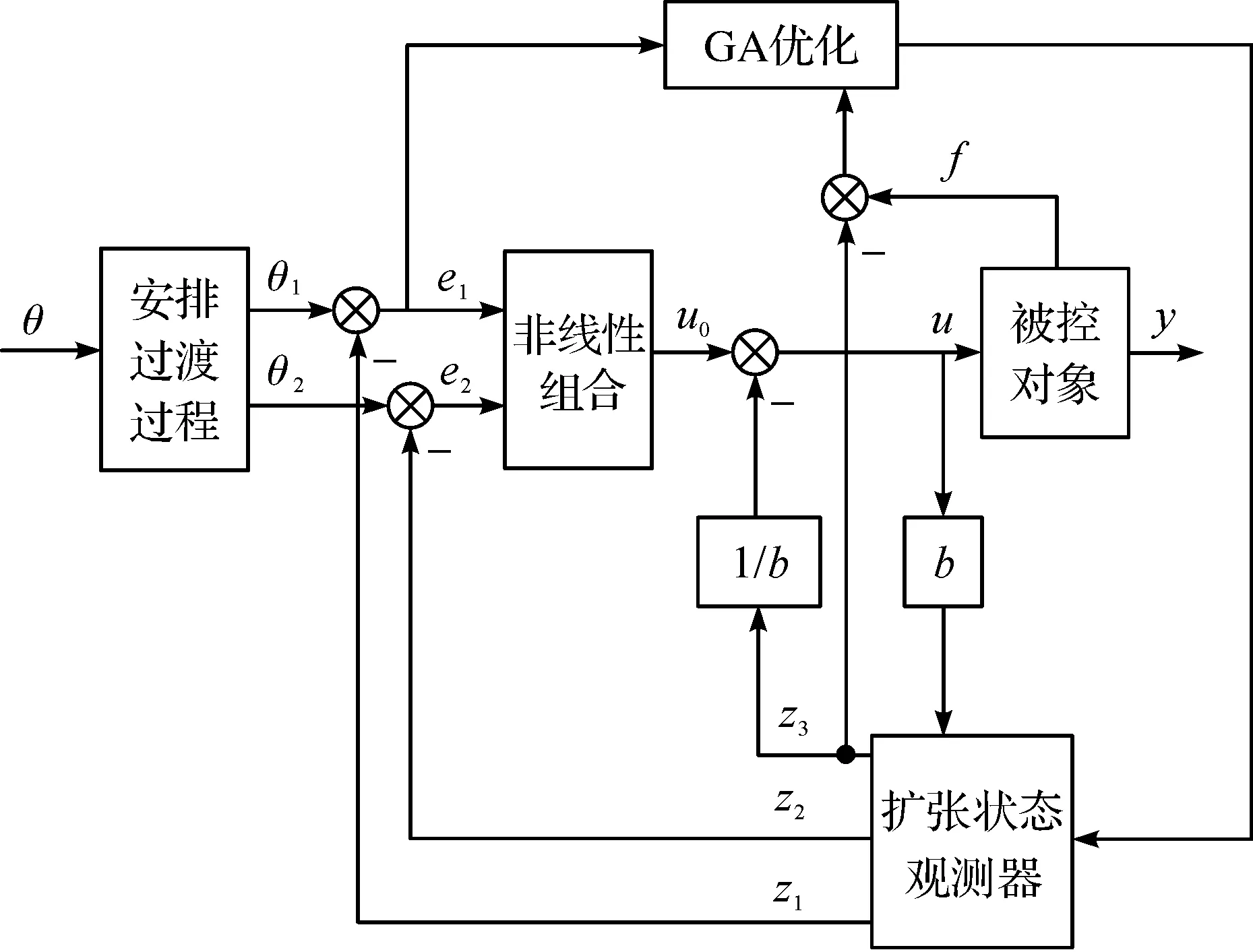
图4 遗传算法优化ADRC参数框图Fig.4 Block diagram of optimizing parameter of ADRC by genetic algorithm

4 仿真及实验分析

永磁同步电机的负载和参数随环境不同而改变，因此仿真中要研究加负载和参数变化时系统的定位精度。在Matlab/Simulink中搭建仿真模型，采用位置环自抗扰控制器，仿真步长h=0.001 s。仿真中所用的PMSM参数如表1所示。

表1 电机参数表Table 1 Motor parameter

ADRC的部分参数采用遗传算法进行优化，为了验证优化后控制器的性能，仿真中其他条件相同，给定位置为5 °，10 °时，比较遗传算法优化后的ADRC控制器与经验整定参数的ADRC控制器的控制性能。对比图如图5所示。

图5 GA优化前后系统位置跟踪Fig.5 System location tracking before and after GA optimization

由图5可得：经过遗传算法优化后的系统跟踪速度明显高于未优化的系统，跟踪误差低于后者，位置为10°，5°时调节时间比经验整定参数的系统分别快0.04，0.03 s。下述关于ADRC位置控制器系统仿真均是优化后ADRC位置控制器。

系统参数转动惯量的变化可能会对控制稳定性造成影响，为了验证ADRC控制系统在参数变化环境下的跟踪精度，给定信号相同时，比较转动惯量为J，2J时系统的位置跟踪情况，如图6所示。

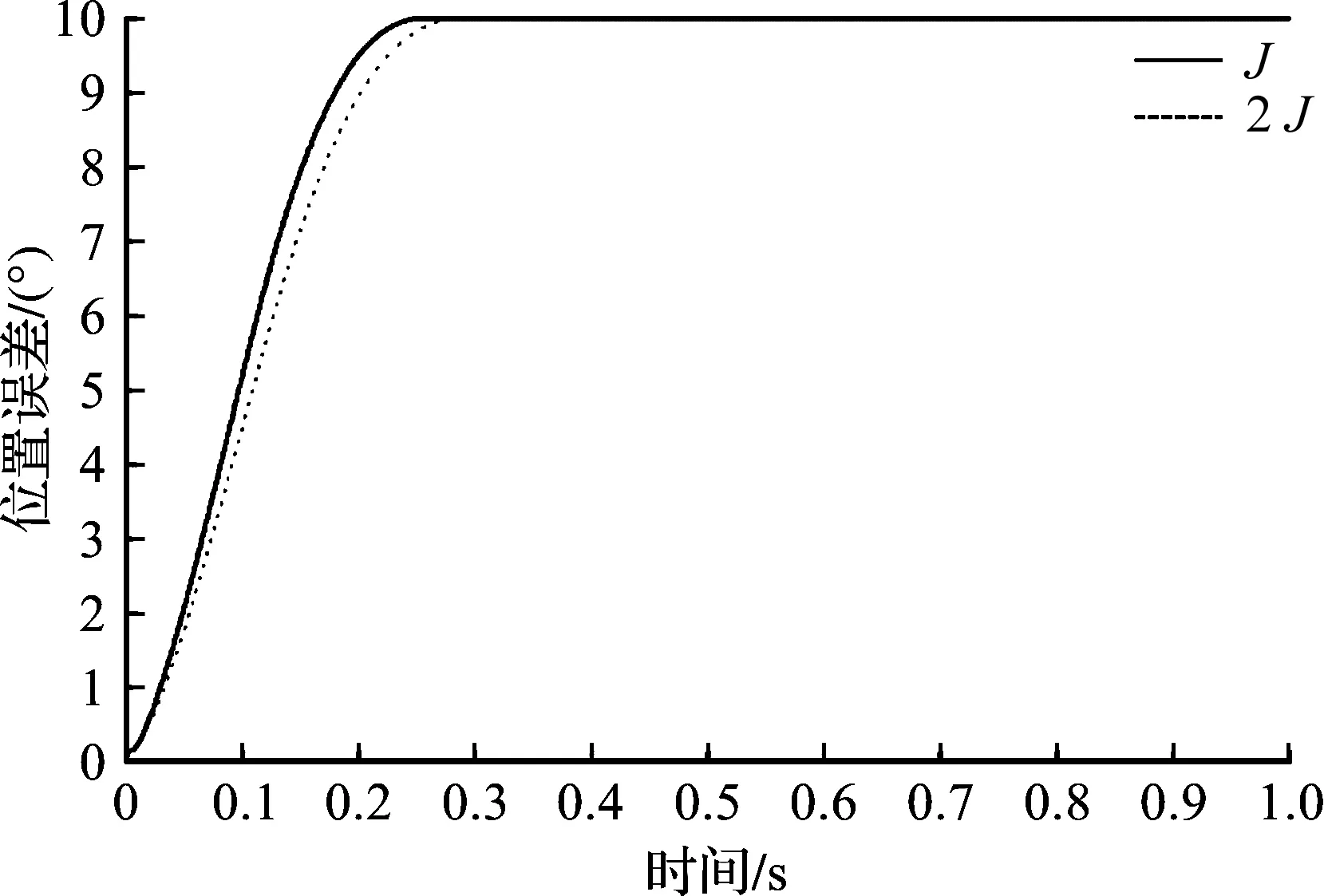
图6 转动惯量分别为J和2J系统位置跟踪Fig.6 Position tracking when the moment of inertia are J and 2J

从图6可得：当系统参数转动惯量变为2J时，调节时间仅下降0.014 s，系统的位置跟踪依然快速稳定，说明系统惯量变化不影响该控制器的性能。

为了验证优化后的ADRC系统在加载后的抗干扰性，其他条件完全相同的情况下，仿真对比了阶跃信号下PID和ADRC控制器在t=0.3 s加载0.2 N·m，t=0.5 s卸载，结果如图7所示。

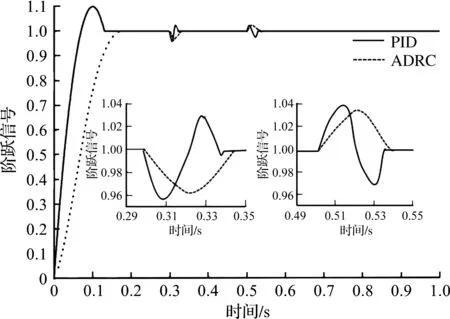
图7 PID与ADRC控制系统抗干扰性能对比Fig.7 Comparison of anti-jamming performance between PID and ADRC

由图7可得：PID控制与ADRC控制相比，到达稳定值的时间快了0.03 s，加载后的调节时间也稍快于ADRC控制，但是不论起动、加载还是卸载后的跟踪曲线都有很大的超调，不能满足跟踪精度要求高的系统。而ADRC控制系统不仅跟踪快速，且没有超调。

上述仿真验证的是输入信号为常值时控制系统跟随性，图8反映输入为正弦变化的信号时系统的连续跟随情况，在t=3 s时加入一个0.2 sint的扰动，观察ADRC和PID控制系统的性能，图9是实际扰动与观测扰动曲线。

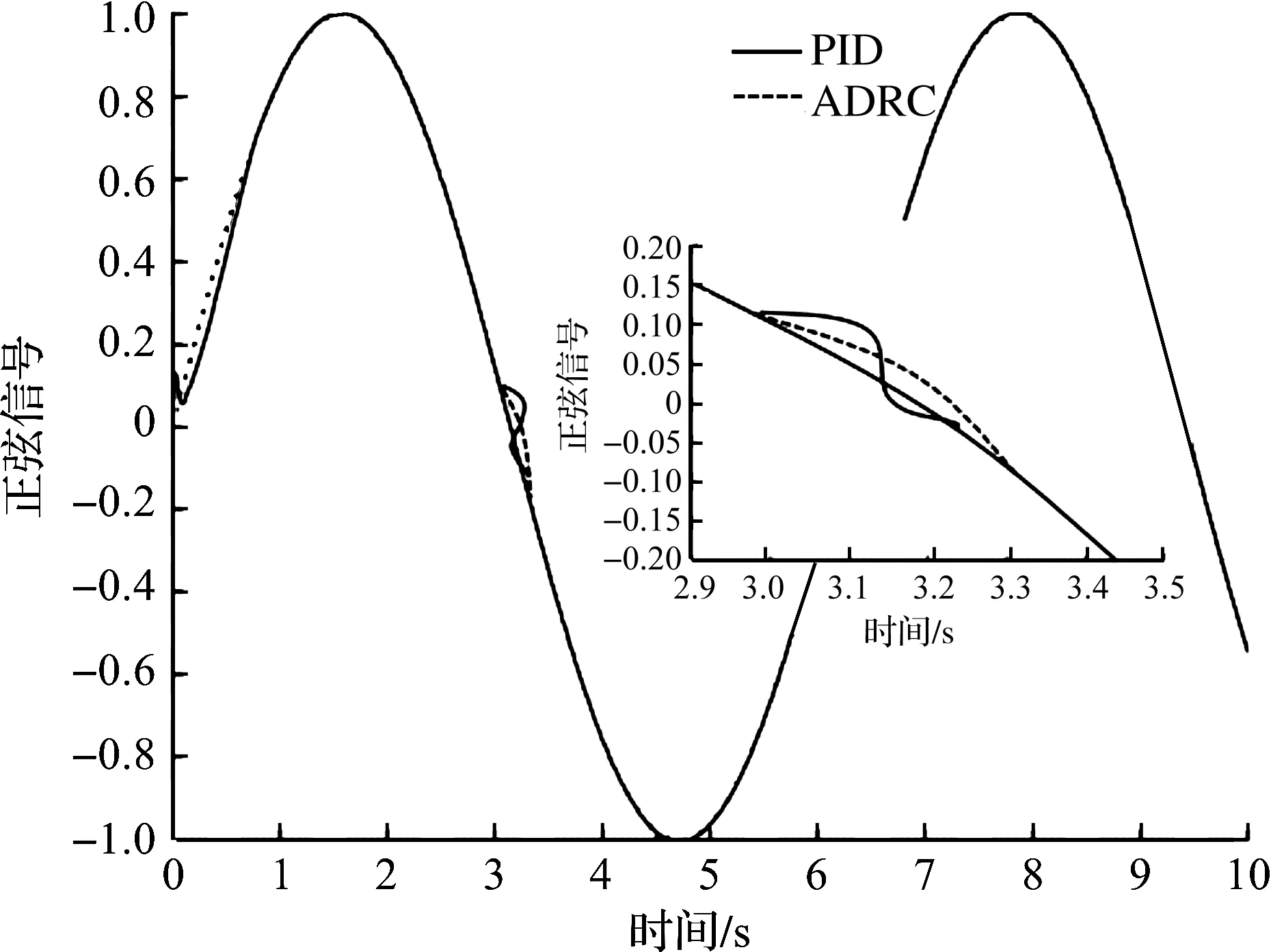
图8 正弦信号下PID与ADRC控制系统抗干扰性能对比Fig.8 Comparison of anti-interference performance between PID and ADRC control system under sinusoidal signal

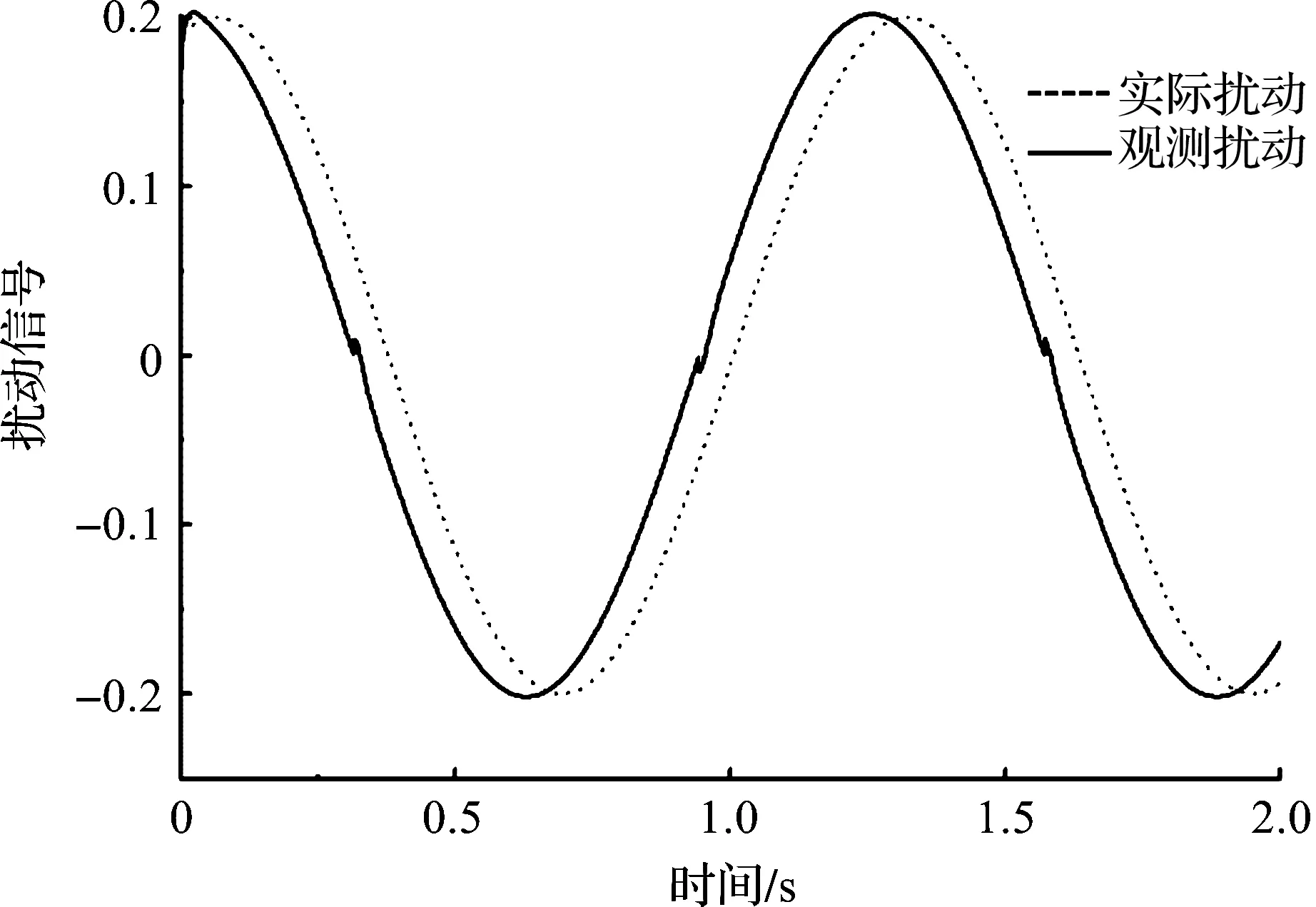
图9 实际扰动与观测扰动Fig.9 Actual disturbance and observation disturbance

从图8可得：正弦信号下，起动时PID控制的稳定性低于ADRC控制，加入干扰信号后，两者均能迅速恢复稳定跟踪，但ADRC的跟踪曲线比较平滑，抗干扰能力强，而PID控制的跟踪曲线波动较大。

伺服电机控制的目标是实现电机无超调和快速响应，为了更有力验证ADRC控制系统在负载扰动下的转速和位置响应性能，搭建测试平台结构如图10所示，PMSM参数与仿真所用电机参数一致，以意法半导体公司的微控制器STM32F407ZGT6作为系统的主芯片，三相逆变器产生六路PWM波形驱动电机转动，采用分辨率为2 048 ppr的增量式光电编码器实现转子位置检测，使用测功机加载需要的负载扰动，并测出实验所需的相关数据。系统采用id=0矢量控制，位置环和速度环采用ADRC控制器一体化控制，电流环采用PI控制器。

实验分别作了2 个验证：给定转子位置为60°，360°，在t=1.5 s施加0.2 N·m的负载，分别得出PID和ADRC控制系统位置响应曲线；给定转速为500，1 000 r/min，在t=1.5 s施加0.2 N·m的负载，得出PID和ADRC控制系统速度响应曲线。对于实验中的数据取关键点进行曲线分析，如图11，12所示。

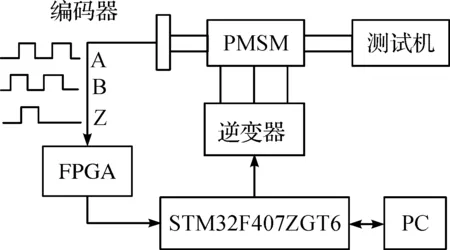
图10 测试平台结构图Fig.10 Structure diagram of Test platform

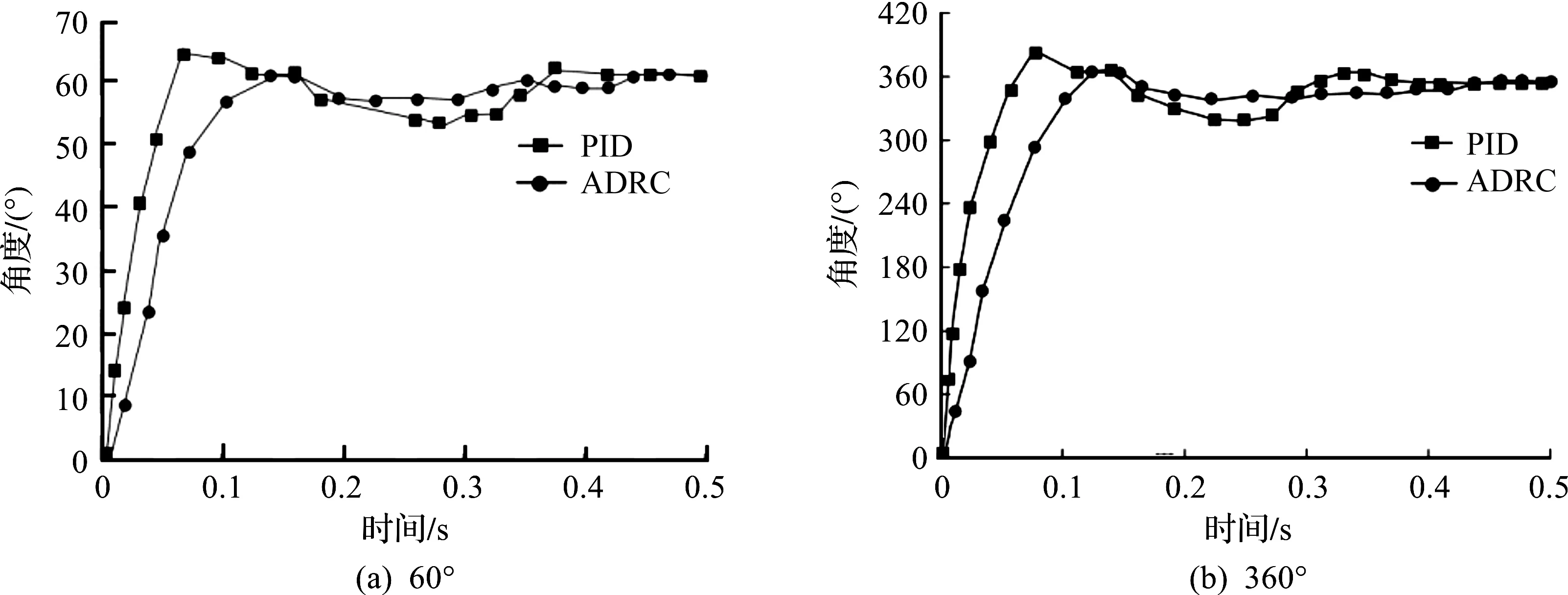
图11 位置响应曲线Fig.11 Response curve of position

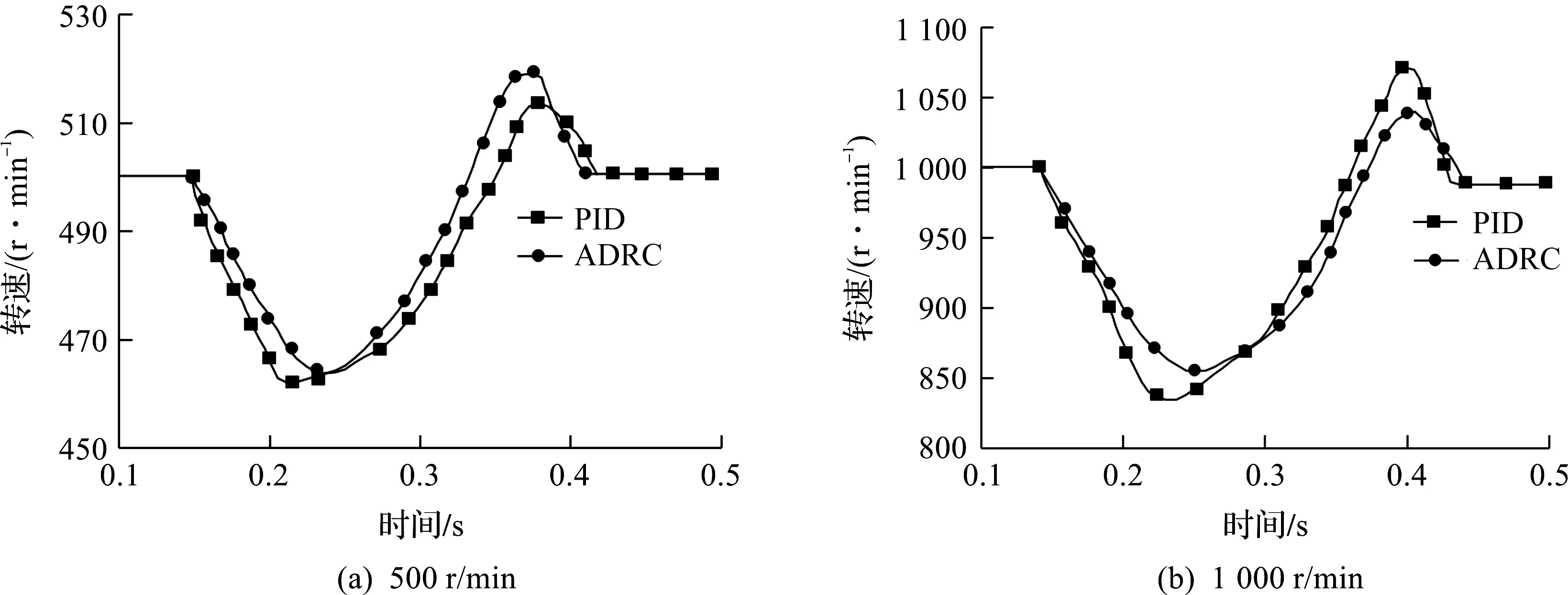
图12 速度响应曲线Fig.12 Response curve of speed

由图11可得：PID与ADRC均能实现快速响应，给定位置为60°时，PID控制和ADRC控制系统分别在0.419，0.426 s恢复稳定值；位置为360°时，PID和ADRC控制系统分别在0.423，0.431 s恢复稳定，但是PID控制存在很大的超调，曲线上下浮动大，ADRC控制系统比较稳定。

系统速度响应曲线如图12所示，在加入负载扰动后，PID与ADRC均能快速稳定，给定速度为500 r/min时，PID和ADRC控制系统分别在0.396，0.401 s恢复稳定；给定速度为1 000 r/min时分别在0.417，0.421 s到达给定值。而PID控制曲线波动比ADRC控制曲线波动大，证明ADRC控制系统控制精度更高，这和仿真结果是一致的。

5 结 论

在PMSM控制系统中，将矢量控制与自抗扰控制原理相结合，设计了永磁同步电机ADRC位置控制器，并用遗传算法解决了自抗扰控制器部分参数靠经验整定的不足。通过仿真对变参数和加负载扰动情况下的系统稳定性进行分析，仿真表明：优化后的ADRC控制系统动静态性能良好，抗干扰能力强、鲁棒性高，可实现无超调快速响应，控制精度高，实验分析结果进一步说明ADRC抗负载扰动能力强，稳定性高。