内压下薄壁锥壳圆筒过渡段变形特征研究

(浙江工业大学 机械工程学院，浙江 杭州 310014)

锥壳是化工设备中常见的结构，该结构的强度问题，倍受人们关注[1-7]，并形成相关的强度评定准则[8]，而对其变形控制准则的研究则较少。在内压作用下，薄壁锥壳圆筒过渡段可能会发生屈曲。Teng等[9-12]及其团队对这一问题做了大量的研究，涉及相关理论分析、模拟计算和临界屈曲压力等方面。Zhao等[13-15]采用实验和模拟分析方法，研究了厚度为1，2 mm，直径为1 000 mm，半锥顶角为40°的薄壁锥壳圆筒内压屈曲问题。从其研究结果来看，考虑实际初始几何偏差与不考虑初始几何偏差对于薄壁锥壳圆筒的内压屈曲变形规律存在较大的差别。然而，基于真实初始几何偏差分布下的变形问题研究相对较少，人们尚没有很好地掌握在内压作用下薄壁锥壳圆筒过渡段变形规律，尤其是用于大型储罐罐顶结构的大锥顶角薄壁锥壳圆筒过渡段变形规律是设计者较为关注的重要问题之一，而目前相关文献非常缺少。

笔者在实验中通过千分表和应变计实验测量了壁厚为1.2 mm，圆筒内径为950 mm，半锥顶角分别为60°和75°的锥壳圆筒过渡段在内部升压过程中的径向位移及应变变化，并采用3D扫描仪扫描获得锥壳圆筒初始和最终几何形貌。采用有限元分析方法对扫描获得的锥壳圆筒模型(含有真实初始几何形状偏差)，进行材料与几何双非线性模拟计算，并与实验结果进行对比，进一步讨论内压下薄壁锥壳圆筒过渡段变形特征。

1 实验方案与装置

1.1 试样尺寸

试样的安排见表1，尺寸图如图1所示。其中，法兰和上盖板为碳钢材料，锥壳和筒节为不锈钢。锥壳和筒节的厚度相同。

表1 试样的几何尺寸及材料性能Table 1 Geometric size and material properties of specimen

图1 试样结构尺寸Fig.1 The structure and the dimensions of specimens

1.2 实验装置

实验装置如图2所示，主要有试样、装置底座上下两部分，它们通过法兰连接，密封件为橡胶密封圈，压力试验介质为水。

1—试样；2—螺栓；3—螺母；4—橡胶密封圈；5—装置底座；N1—进水口；N2—加压口；N3—压力表口；N4—排水口图2 试验装置结构图Fig.2 Structure diagram of testing apparatus

1.3 测量方案与实验过程简述

通过加压泵对装置进行加压，由压力传感器以及压力表记录压力变化，采用应变计和千分表测量锥壳圆筒不同部位的变形及位移情况。

应变计贴点方案为1) 环向布置：在距锥壳与圆筒环焊缝下方20 mm的筒节上，沿环向布置5 个应变计，编号为1～5 #，其中3 #在90°经线上(以锥壳上的纵焊缝为0°计)，相互环向间隔为10°；在距锥壳与圆筒焊缝上方20 mm的锥壳上，沿环向布置5 个应变计，编号为6～10 #，其中编号8 #在90°经线上，互相环向间隔为10°。2) 经向布置：上述3 #和8 #应变计在90°经线上，为进一步考虑经向应变情况，再在8 #应变计所在锥壳90°经线上增加了3 个测点，编号为11～13 #，相互经向间隔80 mm，如图3(a)所示。

千分表布置方案：千分表A，B位于0°经线上，分别在距锥壳与圆筒环焊缝20 mm筒节和锥壳上；千分表C，D位于180°经线上，分别在距环焊缝20 mm筒节和锥壳上；千分表E，F位于-90°经线上，分别在距环焊缝20 mm筒节和锥壳上；千分表G，H也位于锥壳270°经线上，相互经向间隔80 mm，如图3(b)所示。

通过计算机对加压泵进行升压速率的控制，通过千分表、应变仪和摄像头等采集相关数据。其中应变仪为DH3818N-2静态应变测试仪，光栅位移传感器通过RS232串口通讯方式，能实现10 路通道同步采集位移数据，千分表测量精度为0.001 mm，千分表量程为10 mm。将4 个摄像头安装至不同位置，对过渡段各部位进行实时监测。最终连接完毕的实验设备及数据采集仪器如图4所示。

图3 应变计及千分表布置图Fig.3 Arrangement diagram of foil gauge and dial gauge

图4 数据采集设备Fig.4 Data acquisition equipment

在实验前后，分别采用加拿大Creamform公司进口的便携式HandySCAN 3D 激光扫描仪对锥壳筒节表面进行扫描获得整体的初始和最终几何形貌，将实验前的扫描数据通过Geomagic Studio逆向工程软件进行后处理生成IGES格式的文件，从而能在有限元中进行模拟分析。该扫描仪采用多条线束激光来获取物体表面的三维点云，扫描速度达到每秒26.5 W次测量，精度最高可达到0.03 mm，分辨率可达0.05 mm，数据传输速度为1 Gbps。

2 有限元模拟

2.1 几何模型

在有限元软件中导入处理后的实际扫描模型，建立用于模拟计算的几何模型，该模型包含了锥壳圆筒表面的真实初始几何形状偏差。两组试样的有限元模型如图5所示。

图5 两组试样有限元模型Fig.5 Geometric model of two specimens

2.2 模拟参数设置及材料曲线

采用商用的ABAQUS软件进行分析计算，模拟计算的主要参数见表2。材料的真应力应变曲线根据实测值经过换算得到，具体见图6。

表2 有限元模拟分析参数Table 2 Finite element simulation analysis parameters

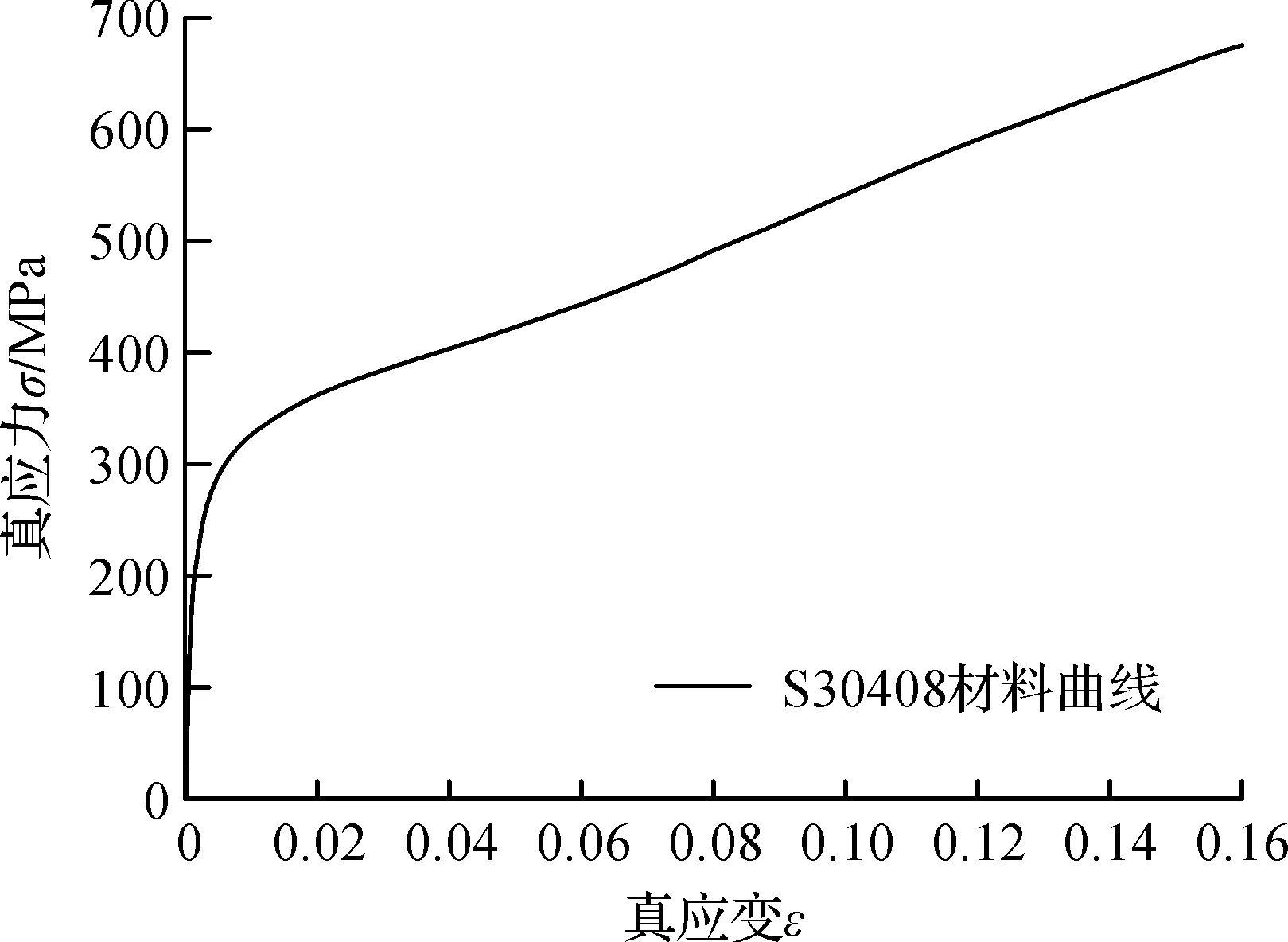
图6 有限元模拟材料曲线Fig.6 Material curve of finite element simulation

3 结果与讨论

3.1 实验现象

在实验中，随着压力的增大，在薄壁锥壳圆筒过渡段将出现屈曲皱褶现象。从回放的录像看，Z120试样目测发生明显皱褶时的压力在0.29 MPa左右，Z150试样目测发生明显皱褶时的压力在0.19 MPa左右。但是这种屈曲变形与外压或轴压失稳现象最大的不同在于，其皱褶变形不是在一个特定压力值下突变产生，而是在一个时间段内，随着压力的升高，从小波慢慢变成明显的大波形。在这个过程中，装置内部也没有出现压力下降的现象，整体结构能继续承载，系统仍处于稳定状态，因此可见这类过渡段的内压屈曲行为具有稳定的特征。

过渡段各测点的应变变化规律是反映变形特征的重要数据，因此将Z120和Z150过渡段各测点的环向应变随压力之间的变化关系绘制成如图7所示的曲线。由于Z150的半锥顶角更大，因此过渡段发生的大变形导致应变波动更为明显。值得注意的是，图7(a，b)中，过渡段上许多测点的应变曲线随着升压而出现先增大后急剧减小再增大的规律，即在曲线中存在导致应变明显改变的拐点。而观察实验后的试样表面，发现这些应变变化明显的测点基本都位于明显屈曲波形发生处附近，且变形越大的位置，其应变变化更为明显，例如Z150试样的1，10 #测点正好分别位于筒节与锥壳的屈曲大波形正中心，因此这两处的应变甚至出现了两次较为明显的突变。两个试样各测点应变发生明显变化时的压力值基本等于目测发生明显变形时对应的压力值，这表明过渡段随着升压发生大变形的局部位置，在屈曲变形的前后时刻，其应变值会出现较为明显的突变。

图7 2 组试样各测点应变—压力曲线Fig.7 Strain-pressure curves of two specimens

3.2 过渡段形貌变化特征

3.2.1 终态几何形貌

两组试样经实验最终形貌变化如图8(a，c)所示，过渡段波形分布具有一定的周期性，但是相互间距不等，环向呈不均匀分布，在锥壳和筒节上均可见到大小不一的起皱波形。图8(a，b)为Z120试样0°经线所在区域实验与模拟得到的最终几何形貌对比，以0°纵焊缝为基准，整个过渡段环向全范围共计17 个屈曲波形，而观察右图同样范围内，有限元模拟得到的屈曲波形的数量和角度与实验基本相同，而整个环向全范围最终失稳波数也是17 个。同时对于波形的不同形状，例如0°焊缝处的棱形波形，有限元模拟结果依然与实验结果吻合。对于Z150来说，从屈曲波形的数量、角度、形状上来看，模拟与实验两者结果依旧相近，对比图8(c，d)中过渡段0°处模拟与实验得到的较大波形，更加可以看出有限元对于每个位置发生变形的程度也有着准确的预测。

图8 薄壁锥壳圆筒过渡段屈曲现象Fig.8 Buckling phenomenon of thin wall cone-cylinder intersections

3.2.2 径向位移随升压的变化

为了更好地分析过渡段变形问题，选取屈曲波形明显发生处的测点位移数据进行分析讨论。就Z120试样而言，千分表测点A，B落在实际波形发生处，同样，千分表测点C，D落在Z150试样实际波形发生处。图9为两个试样以上测点径向位移变化和升压压力之间的关系。在图9中所列的范围内已有明显起皱屈曲现象，位移都已达最大量程。

从图9中可以看出：两组试样尺寸不同，但是有限元对于对应A，B，C，D各测点位移变化的模拟结果与实验测量值依旧较接近，这表明数值模拟计算方法不仅能对过渡段变形后终态几何形貌作出较准确的预测，而且对于各个部位的变形过程也能较为准确地进行模拟计算。将从录像中观测到两个试样明显起皱时的压力值P目测，以及根据图9(a)中的SA-test和图9(b)中的SC-test位移变化曲线采用两倍斜率法得到的压力值P两倍斜率法分别在图9(a，b)中标出，可以看出采用两倍斜率法得到的压力值要小于试样发生观测到明显变形时的压力值。

图9 两组试样各测点位移—压力曲线Fig.9 Displacement-pressure curves of two specimens

为了更加详细地了解薄壁锥壳圆筒过渡段在内压作用下的变形情况，图10，11分别画出了Z120和Z150两组试样在不同内压下模拟所得的距焊缝20 mm处筒节和锥壳上整个环向的形状变化曲线。

先对图10，11中各坐标、曲线和标记点进行说明，横坐标都是以锥壳表面纵焊缝处为0°，逆时针方向至180°，顺时针方向至-180°；纵坐标的0 刻度代表该截面处完美半径，因此初始外形(最上方实线)即是圆周方向各点的初始几何偏差，正负值即是初始向内外的偏差数值。中间的各种虚线分别是通过模拟计算得到的不同压力下的形状变化曲线，直到模拟压力值等于实验终止压力(粗虚线)。最终外形(最下方粗实线)为实验结束后，通过扫描获得的试样表面变形后的几何形貌。同时将过渡段各处的千分表测点位移与对应位置的初始值进行相加也在图中标出。

从图10，11中可以看出：两个试样的圆筒部分初始几何偏差整体都要小于各自锥壳部分。但是无论是哪个区域，在模拟计算中，随着压力的上升，过渡段上具有初始上下偏差的部位开始慢慢出现明显的变形特征，从最终模拟外形曲线和实测外形曲线中可以明显看出：相比初始外形，环向整体形状发生了显著的变化，出现了大小不一的波峰与波谷，尤其是在0°焊缝附近。观察模拟与实际终态形貌的对比，发现模拟与实验结果两者吻合度较好，对于过渡段最终几何形貌的高低起伏，模拟计算做到了很好的预测。观察不同位置的千分表读数标记点，可以看到在不同压力值下，各测点位移读数基本都落在了对应的模拟曲线上，这表示模拟计算得到的整个环向各处变形规律与真实变形情况接近。

图10 Z120过渡段形状变化Fig.10 Shape changes of Z120 transitional sections

图11 Z150过渡段形状变化Fig.11 Shape changes of Z150 transitional sections

从以上两个试样锥壳圆筒过渡段的变形问题研究中，可以发现：通过有限元模拟不同位置环向形状随着压力的变形过程以及得到最终外形轮廓，能与对应的实验结果有较高的吻合度。这表明数值模拟方法能对锥壳圆筒过渡段内压失稳而导致的大变形问题进行有效的模拟计算。而在过渡段具有一定初始几何偏差的部位，特别是焊缝附近，最终都会发生明显的屈曲变形形成波峰或波谷，因此初始几何偏差对于薄壁锥壳圆筒过渡段屈曲变形的影响非常显著。

4 结 论

以两组薄壁锥壳圆筒结构为研究对象，对其过渡段在内压作用下的屈曲大变形问题进行研究，通过内压实验获得过渡段各个位置应变—压力和位移—压力曲线，并采用三维扫描仪分别对实验前后锥壳圆筒表面进行扫描获得其初始和最终几何形貌，在有限元软件ABAQUS中对含真实几何偏差的锥壳圆筒模型进行材料和几何双非线性模拟计算，并与实验数据进行对比，结果表明：薄壁锥壳圆筒过渡段随着内压的增大会出现屈曲变形的现象，环向形成大小不一，呈一定周期性不均匀分布的波形，但由于结构仍具有承载能力，因此这类屈曲行为具有稳定的特征；过渡段局部位置的应变值会在发生屈曲大变形的时刻出现明显的突变，且初始几何偏差是影响形貌变化的重要因素；对含真实几何偏差模型进行模拟计算得到的过渡段最终几何形貌与实测值相近，而且径向位移变化规律也与实验结果吻合，进一步表明可采用材料和几何双非线性模拟计算方法来分析薄壁锥壳圆筒变形问题，这有助于优化相关结构设计以及对相应标准规范进行更为合理的制定。