一类具有B-D发生率的随机SIQS模型的动力学行为研究*

胡晶晶韦煜明彭华勤

(广西师范大学 数学与统计学院，广西 桂林 541004)

0 引言

传染病作为一种常见病和多发病，是世界上造成死亡的第二大原因，所以传染病的预防和控制就尤为重要，为了减少易感人群被感染的风险，隔离感染者是一种有效控制疾病传播的方法.自Kermack和Mc Kendrick[1]提出SIR仓室模型以来，大量的数学模型被建立并用来描述传染病动力学，[2-6]帮助制定有效的措施来控制传染病的传播，所以数学模型在流行病学研究中发挥着重要作用.近些年来各种流行病模型的提出和广泛探索，使得疾病防治研究取得了很大进展.魏等人[7]提出了一个具有校正隔离率的SIQS模型：

其中，S(t)为易感者在t时刻的人口数量，I(t)为t时刻染病者的人口数量，Q(t)为在t时刻已接受隔离的人口数量，参数Λ，d1，d2，d3，为正常数，δ，ε，γ，a1，a2为非负常数，Λ为人口输入率，β为易感者与染病者的接触率，d1为易感者的自然死亡率，d2为感染者由疾病引起的死亡率，d3是隔离者由疾病引起的死亡率，δ为感染者的隔离率，γ，ε分别是感染者与隔离者重新回到易感者的比率，表示的是不含隔离者，且依赖易感者和感染者的校正隔离率，B i(i=1，2，3，4)是独立的布朗运动，代表白噪音的强度.魏等人讨论了解沿无病平衡点灭绝的充分条件以及正解的平稳分布.Cao等人[8]研究了带有quarantine-adjusted发病率的SIQR传染病模型，此时接触率为，并对接触率和种群白噪音扰动，得到了疾病灭绝与遍历分布的充分条件.基于以上学者的研究，本文讨论了带有Beddington-DeAngelis发生率的SIQS传染病模型，对接触率β白噪音扰动，即，并假设随机扰动对每个种群是线性扰动，因此得到如下模型：

d是自然死亡率，α是因病死亡率，且，其他参数含义与模型(1)相同.

本文通过构造合适的Lyapunov函数，利用Itô公式，鞅的强大数定理等相关的随机微分方程的知识，讨论在一定条件下随机SIQS系统(2)的消亡与存在遍历性平稳分布问题.

1 全局正解的存在唯一性

1.1 预备知识

令(Ω，F，{F}t≥0，P)是完备概率空间，函数B i(t)(i=1，2，3，4)是定义在完备概率空间上的标准布朗运动，令X(t)是d-维的Ito过程，则

令V∈C2，1(R d×[t，∞];R+)，则V(X，t)也是Itô过程且定义如下：

对于系统(2)这样一个随机微分方程，我们首先考虑其解的存在唯一性.

1.2 全局正解的存在唯一性

定理1对任意初值，系统(2)存在唯一的全局正解(S(t)，I(t)，Q(t))，并且该解依概率1位于中，即.

证明：因为系统(2)的系数满足局部Lipschitz条件，不满足线性增长条件，则对任意初值，系统(2)在[0，τe)上存在唯一的局部解，τe为爆破时刻.为了证明解是全局的，我们只需证τe=∞.a.s.设η0＞0且满足S(0)＞η0，I(0)＞η0，Q(0)＞η0，对任意η≤η0，定义停时列：

记infΦ=∞(Φ表示空集).由停时的定义知，当η→0时，τη单调递增.令，显然τ0≤τe，若能证得τ0=∞.a.s.则τe=∞.a.s.故只需证明τ0=∞.a.s.现用反证法证明，如果τ0＜∞，则存在T＞0和ζ∈(0，1)，使得P(τ0≤T)＞ζ，因此存在一个正整数η1∈(0，η0)使得当η∈(0，η1)时，

定义一个C2函数：

根据Itô公式可得

其中

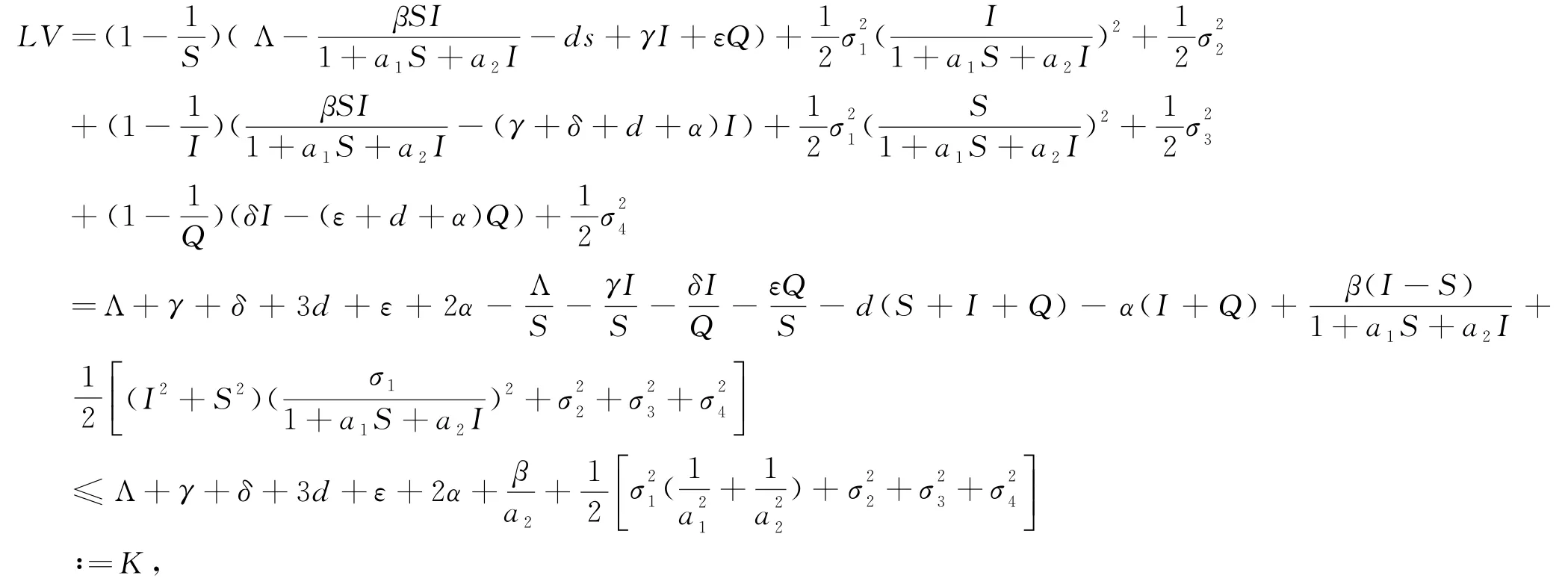
因此，

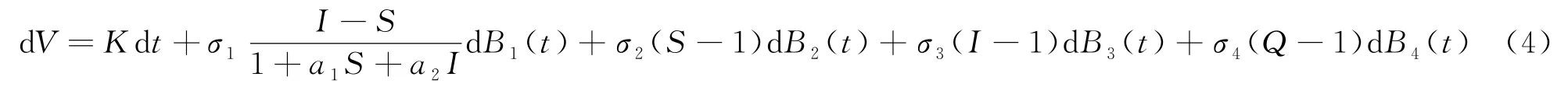
对(4)式两边同时从0到τη∧T积分，有

对上式取期望，则有

设Ωη={τη≤T}，则P(Ωη)≥ζ，对每个ω∈Ωη，由停时的定义可知，在S(τη，ω)，I(τη，ω)，Q(τη，ω)中至少有一个等于η，所以

由(5)可知，

所以τ0=∞.a.s.即系统(2)存在全局唯一正解.

2 遍历平稳分布

定义阈值为：

定理2令(S(t)，I(t)，Q(t))是系统(2)关于初值的解，如果

疾病存在遍历性平稳分布，即疾病持久.

这里θ1是足够小的正常数.在集合选择足够小的θ1满足下面的条件：

这里M＞0，F是正常数，且满足

首先给出系统(2)的扩散矩阵：

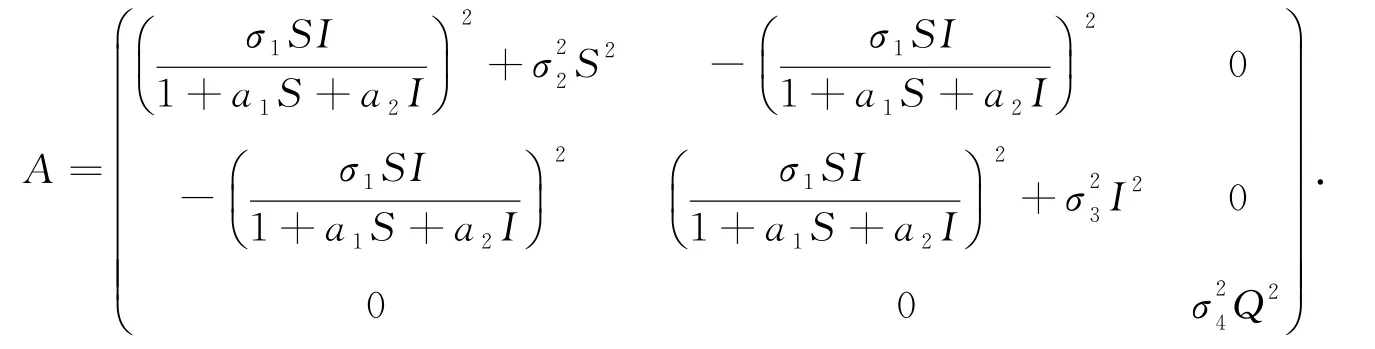
由系统(2)和Itô公式可知，

定义C2函数，

这里c1，c2是正常数，根据公式Itô可知

即(14)式可写成

且M满足(12)式，则有，

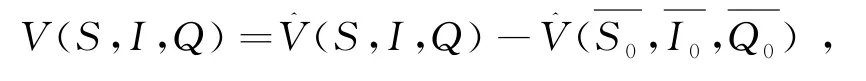
因此，

接下来考虑下面4种情况.

情况1：如果(S，I，Q)∈D1，有

综合(9)可得

情况2：如果(S，I，Q)∈D2，有

因此

情况3：如果(S，I，Q)∈D3，有

情况4：如果(S，I，Q)∈D4，有

结合(16)(17)(18)(19)可知，系统(2)存在遍历性平稳分布，即疾病持久.

3 疾病的消亡

流行病爆发时，不只需要研究疾病的持久性，更重要的是讨论疾病在什么条件下消亡，本节主要讨论系统(2)的消亡.

定理3如果对于任意给定的初值是系统(2)的解，若

证明：应用Itô公式可得

对(23)式从0到t积分得

考虑在条件(21)下，

对(26)式两边同除以t并令t→∞，又由(25)有

对(27)式两边同时取极限并除以t，由(22)(25)，则

4 数值模拟与结论

利用Euler Maruyama(EM)方法[10]和Matlab软件数值模拟在不同白噪声下疾病遍历平稳分布和消亡问题，首先给出系统(2)的离散化形式：

其中ζk(k=1，2，3，…)是服从N(0，1)分布的高斯随机变量.

考虑疾病的遍历平稳分布，参数取值如下：Λ=1，d=0.2，β=0.66，a1=1，a2=1，σ1=0.01，σ2=0.002，σ3=0.2，σ4=0.3，δ=0.1，α=0.01，γ=0.1，ε=0.004，

由图1可知疾病持久，验证了定理2.

图1 系统(2)在初值为(2.4，2.4，1.2)时S(t)，I(t)，Q(t)的轨迹图Fig.1 The path of S(t)，I(t)，Q(t)for system(2)with initial values

考虑疾病的消亡情况，取参数如下：Λ=0.1，d=0.15，β=0.15，a1=1，a2=2，δ=0.004，α=0.25，γ=0.1，ε=0.004，σ2=0.002，σ3=0.2，σ4=0.3.

图2 系统(2)在初值为(2.4，2.4，1.2)和σ1 分别为0.1(a)，0.45(b)时S(t)，I(t)，Q(t)的轨迹图Fig.2 The path of S(t)，I(t)，Q(t)for system(2)with initial values with(2.4，2.4，1.2)

本文主要讨论了Beddington-De Angelis发生率的SIQS传染病模型的动力学行为，证明了随机系统(2)存在唯一的全局解，得到了基本再生数在一定条件下可控制疾病遍历性平稳分布和消亡，并且发现大的随机白噪声会抑制疾病的爆发，这在生物学意义上为我们提供了控制疾病的有效方法.