基于自抗扰终端滑模的高速滑翔飞行器姿态控制*
2019-06-08安炳合王永骥侯治威
安炳合,王永骥,刘 磊,侯治威,王 博
(华中科技大学自动化学院, 武汉 430074)
0 引言
高速滑翔飞行器是指飞行速度为5~20Ma的滑翔飞行器。凭借突出的飞行速度,高速滑翔飞行器可以突破反导系统的拦截,实现精准快速的目标打击,因此受到了越来越多的关注。高速滑翔飞行器的运动过程中受到众多不确定因素的影响,因此对其的控制系统需要具有一定的鲁棒性。
滑模控制[1]方法是一种非线性鲁棒控制方法。其基本思想是设计非线性控制律使系统状态运动到预先设计的滑模面上并进行滑模运动,最终收敛到平衡点。系统在滑模面上的运动不受外界干扰的影响,具有较强的鲁棒性。终端滑模方法通过在滑模面中引入误差的非线性项作为终端吸引子,保证系统误差能够在有限时间内收敛,改善系统的性能。Eshghi S等[2]针对卫星的姿态控制问题提出一种非奇异终端滑模控制方法,避免了传统终端滑模控制当误差趋于零时控制量会趋于无穷大的奇异问题,同时收敛时间上限能够计算出来。
自抗扰控制(ADRC)是韩京清提出的一种不需要知道被控对象精确模型的控制方法[3],由微分跟踪器(TD),扩张状态观测器(ESO)以及非线性状态误差反馈控制器(NFC)组成。相比于传统PID控制器,自抗扰控制器能够实现更好的控制效果。Chang K等[4]在四旋翼飞行器的避障问题中,设计了自抗扰解耦控制器,能够消除由系统内部和外部干扰引起的状态耦合和不确定性的影响。在有风力干扰与噪声的情况下,飞行器能够快速跟踪指令信号,为成功避障提供了保证。
文中针对高速滑翔飞行器姿态控制问题,设计一种终端滑模控制与自抗扰控制相结合的复合控制方法。利用微分跟踪器安排指令信号的过渡过程,兼顾系统响应的快速性与超调量。使用扩张状态观测器对外界干扰与参数不确定进行观测。基于终端滑模的思想设计控制律,利用扰动的估计值在控制律中进行补偿,提高系统的鲁棒性,并降低控制器输出的抖振。
1 高速滑翔飞行器运动模型
高速滑翔飞行器在运动过程中主要受到空气动力的作用。将空气动力沿速度坐标系分解可得沿速度方向的阻力D,垂直于速度方向向上的升力L。根据飞行器动力学分析,可得飞行器在纵向平面的运动模型为:
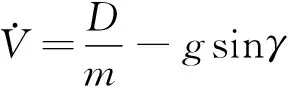
(1)
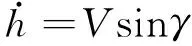
(2)
(3)
(4)
式中:V为飞行器速度;h为飞行器高度;R为航程;R0为地心半径;γ为弹道倾角;m为飞行器质量;g为飞行器所处位置重力加速度;g0为标准重力加速度。
在飞行过程中,改变飞行器升降舵、方向舵以及副翼的偏角,可以改变飞行器受到的气动力矩。将飞行器受到的力矩沿机体坐标系3个坐标轴分解分别可得滚转力矩Mx、俯仰力矩My、偏航力矩Mz。
根据动量矩定理可得飞行器的姿态运动模型[5]为:
(5)
(6)
(7)
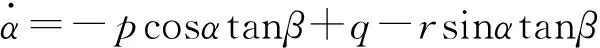
(8)
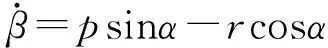
(9)
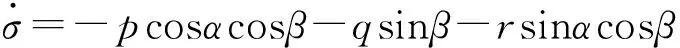
(10)
式中:β为侧滑角;σ为倾斜角;α为攻角;p、q、r分别为滚转角速率、俯仰角速率与偏航角速率;Iij(i=x,y,z;j=x,y,z)为飞行器的转动惯量 。
考虑飞行过程中的外界干扰与飞行器自身参数的不确定,在方程中引入扰动项,得到以下的高速滑翔飞行器姿态控制模型[6]:
(11)
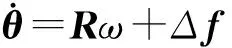
(12)
式中:θ=[αβσ]T,ω=[pqr]T,Δd=[Δd1Δd2Δd3]T与Δf=[Δf1Δf2Δf3]T代表外界环境与参数的不确定对飞行器的影响,M=[MxMyMz]T。
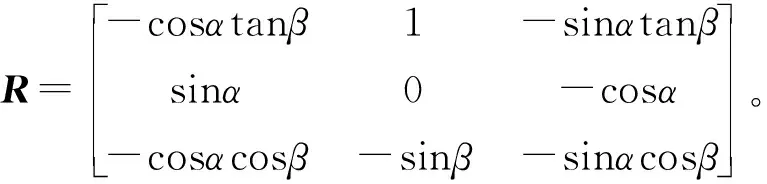
2 高速滑翔飞行器姿态控制器设计

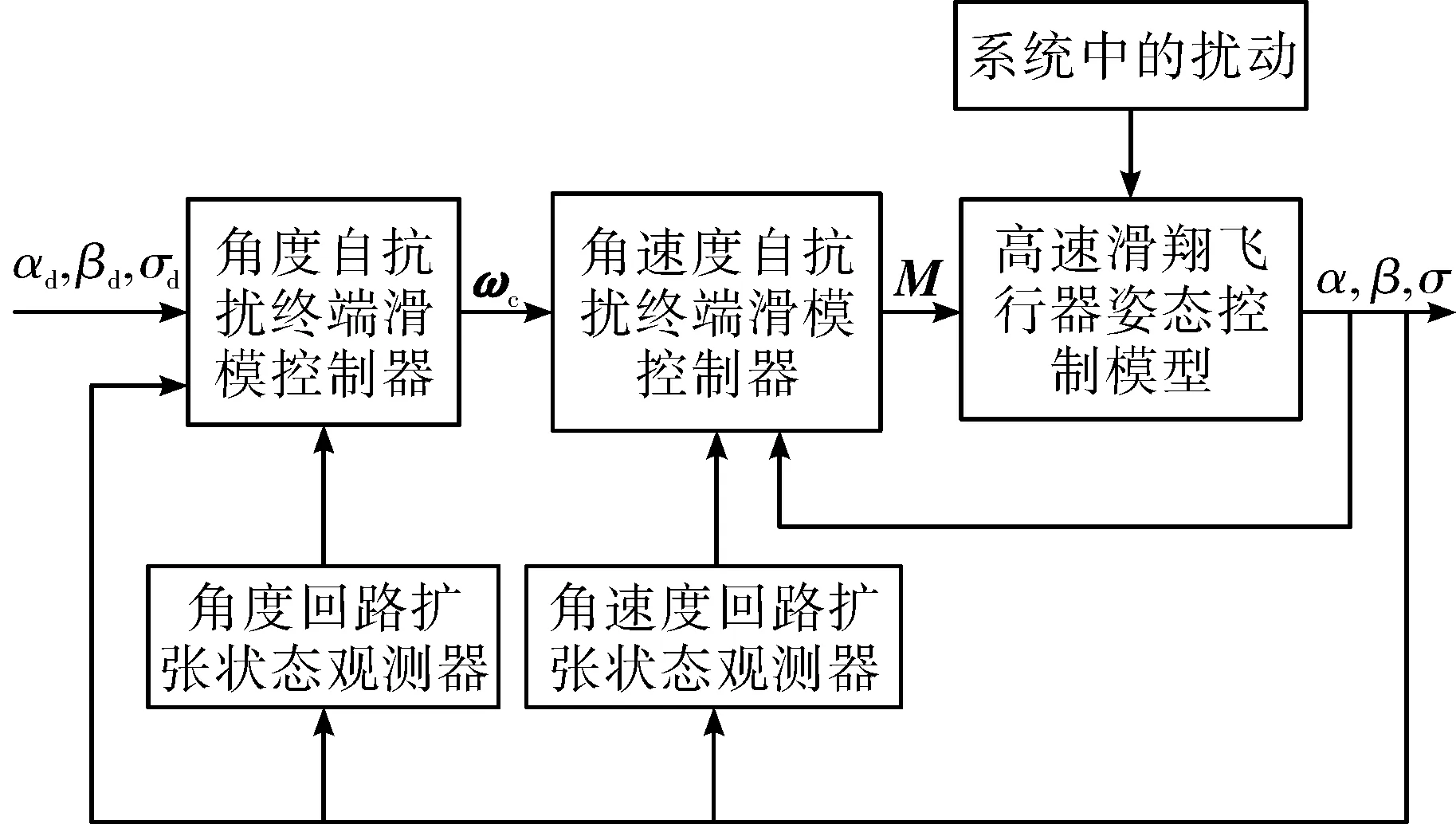
图1 姿态控制系统结构图
2.1 角度控制回路自抗扰终端滑模控制器设计
高速滑翔飞行器本身质量较大,具有较大的惯性,在快速响应过程中会产生一定超调量,不利于飞行器的稳定。文中利用跟踪微分器安排指令信号的过渡过程,以实现系统快速响应与降低超调量的目的。
角度回路二阶跟踪微分器设计为如下形式:
(13)
式中:θd为期望的角度指令,υ1∈R3×1为θd的跟踪值。fh(e1,υ2,r0,h)=[fh(e11,υ21,r0,h),fh(e12,υ22,r0,h),fh(e13,υ23,r0,h)]T。其中υ2 i(i=1,2,3)为υ2的3个分量。
fh是最速控制综合函数[7],其表达式如下:
(14)
式中,r、h为给定参数。
基于终端滑模方法设计非线性控制律,针对姿态角度运动,设计如下的非奇异终端滑模面:
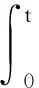
(15)
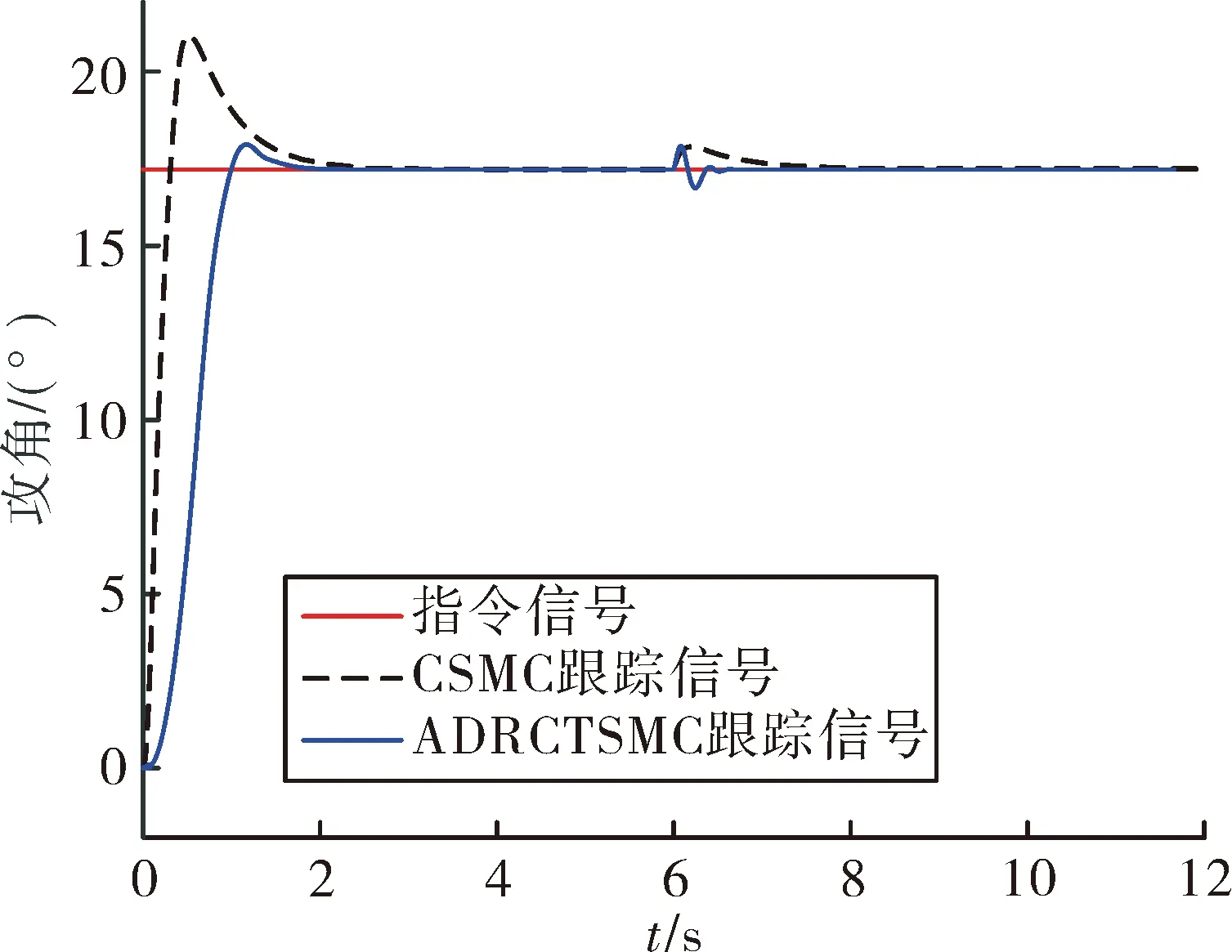
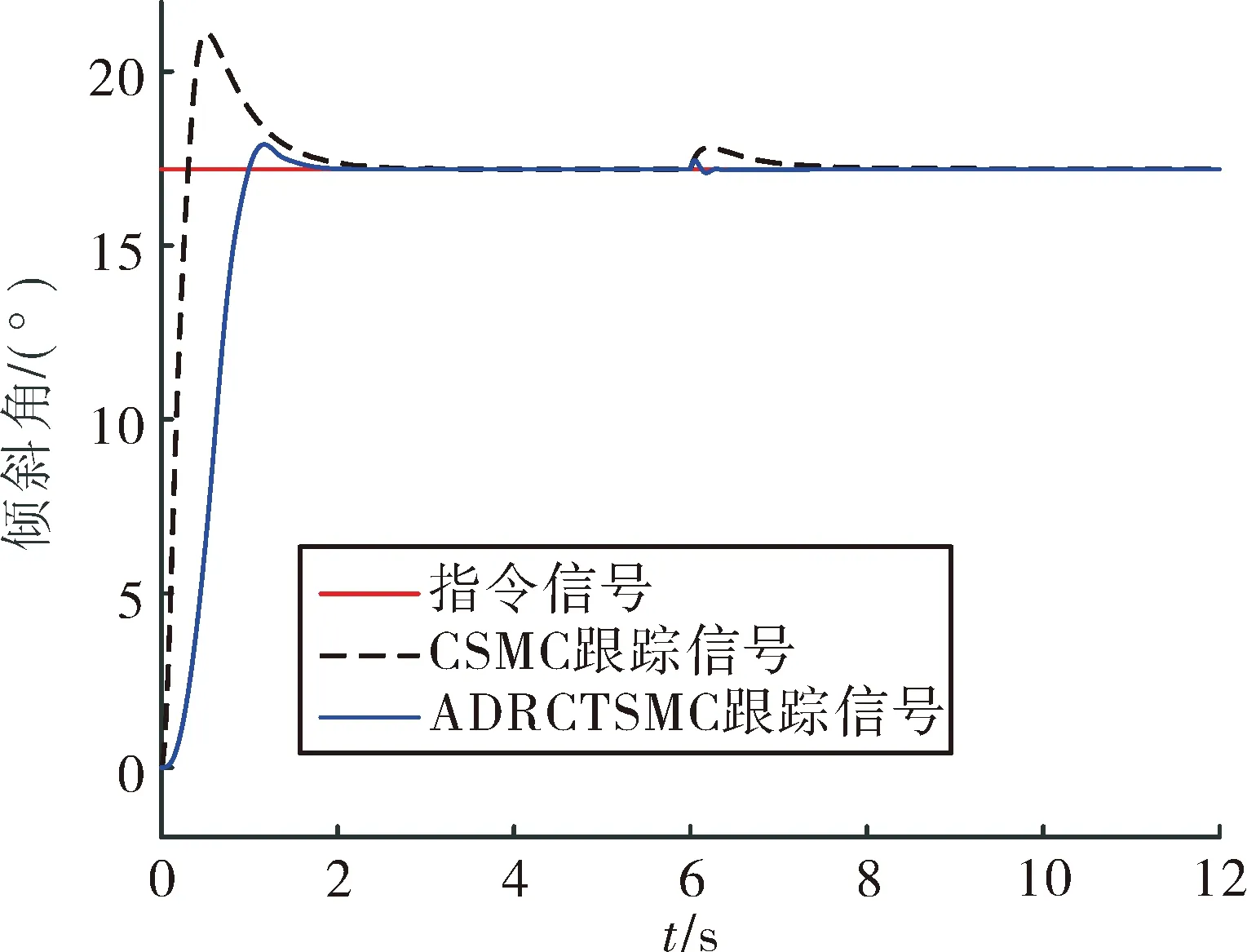
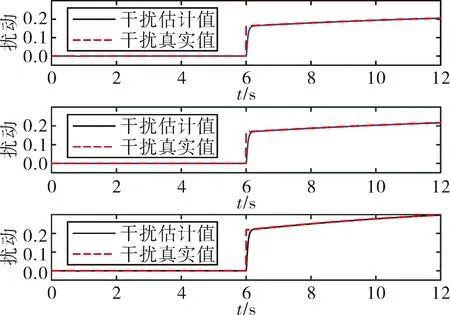
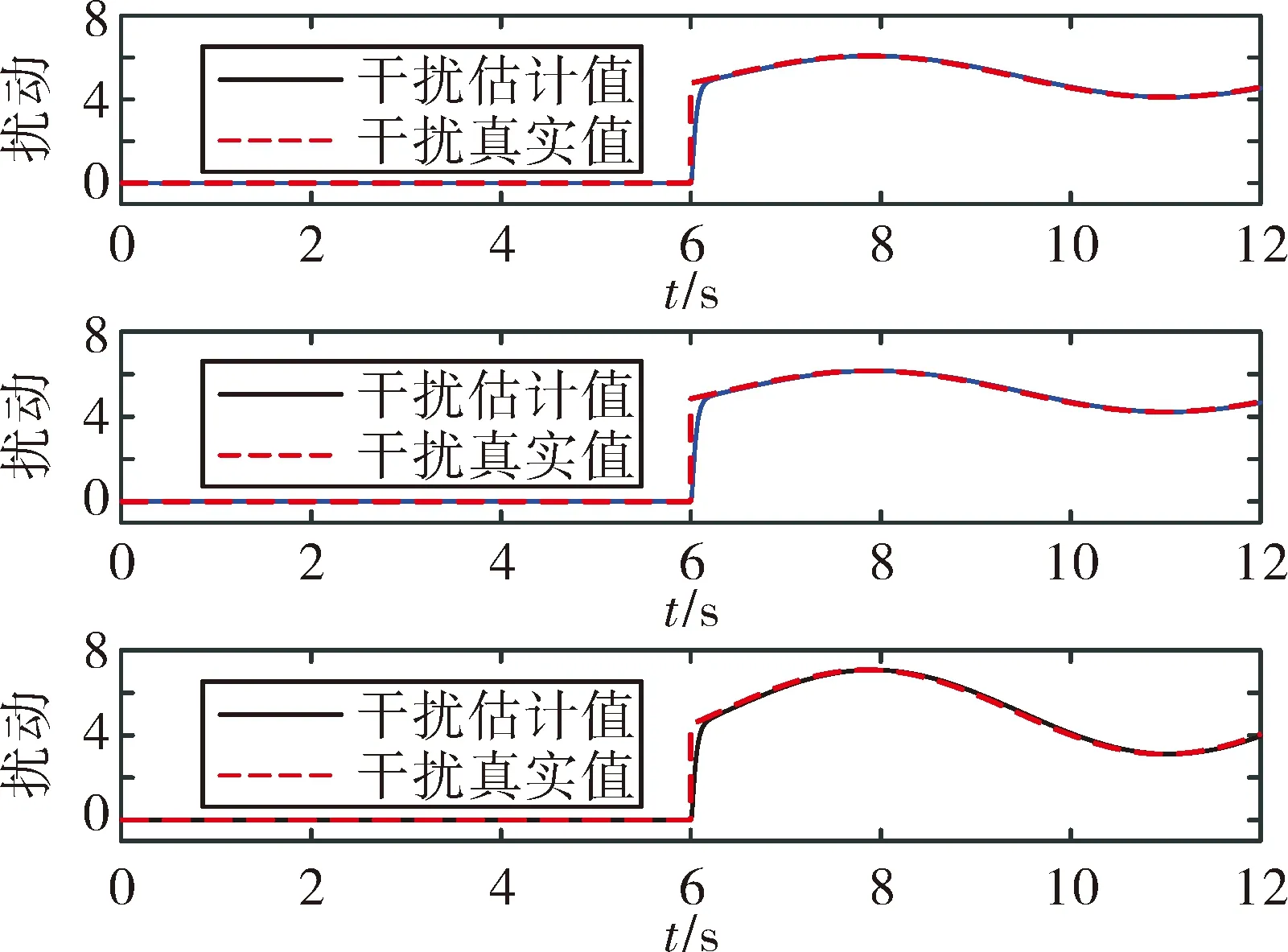
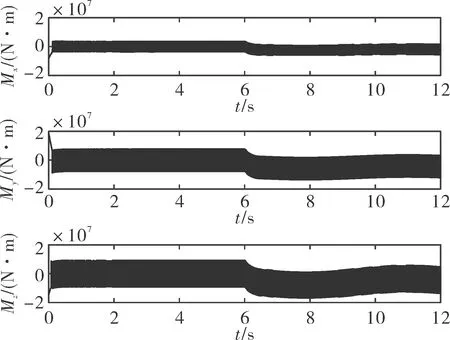
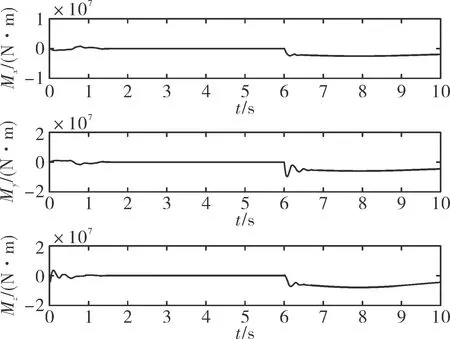
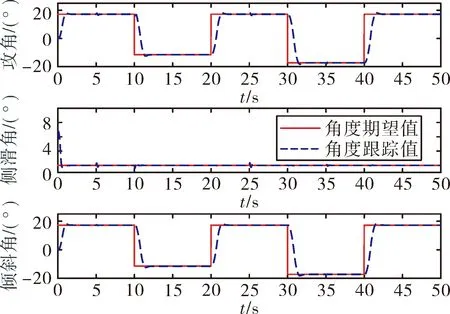
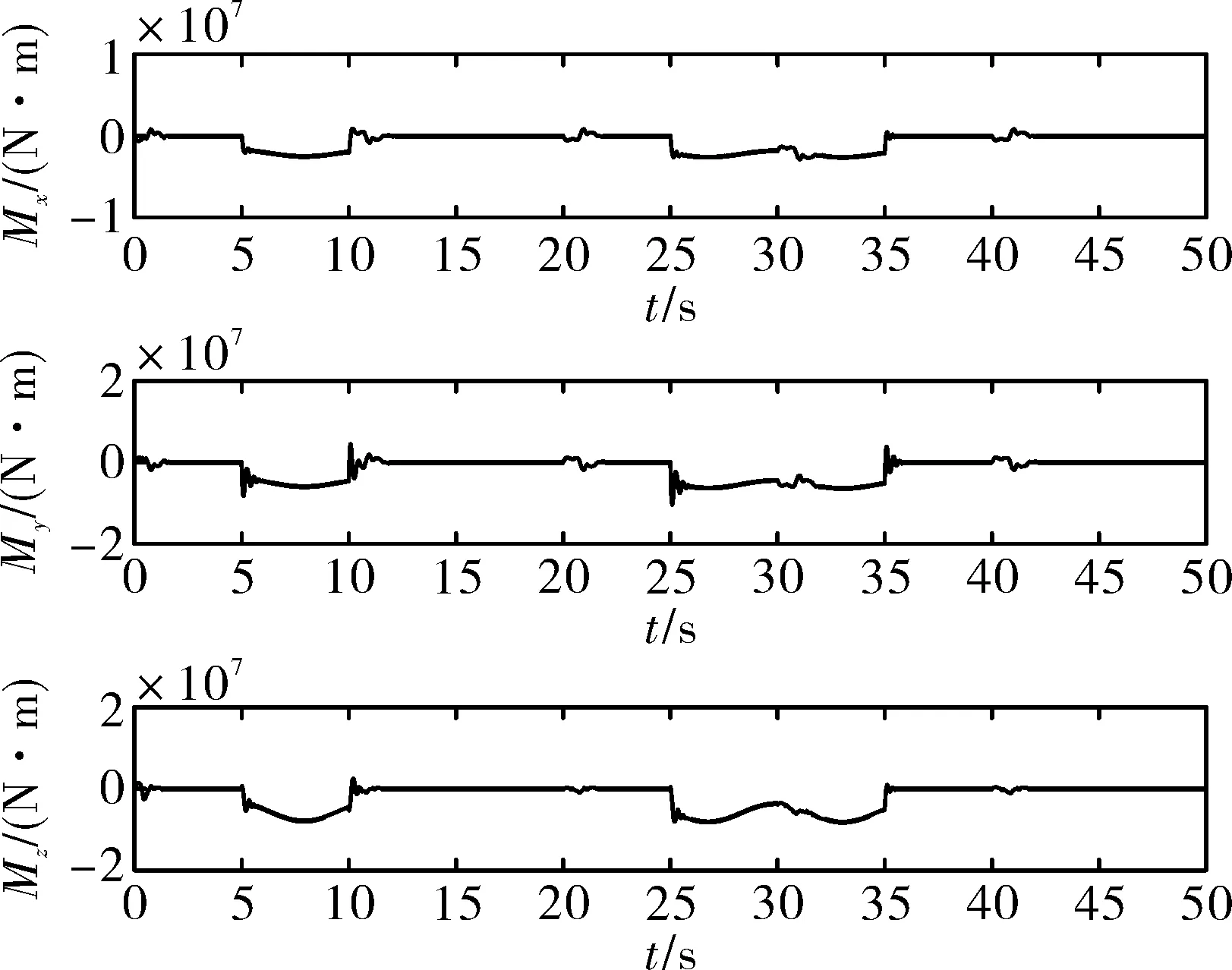
式中:s1∈R3×1,θe=θ-θd,θe0为初始状态误差,γ1、γ2为正对角矩阵,且γ1=diag(γ11,γ12,γ13),γ2=diag(γ21,γ22,γ23), 0 设计如下的非线性控制律: (16) 式中:k1、k2为正对角矩阵,k1=diag(k11k12k13),k2=diag(k21,k22,k23),z2=[z21z22z23]T为干扰Δf的估计值,sign(s1)=[sign(s11),sign(s12),sign(s13)]T。 假设干扰Δf有界,将外界的干扰作为一个新的系统状态,通过设计扩张状态观测器对新的系统状态进行观测。扩张状态观测器的设计如下: (17) 式中:z1∈R3×1为θ的估计值;b01、b02为正对角矩阵,且b01=diag(b011,b012,b013),b02=diag(b021,b022,b023);fal(e2,λ1,δ1)=[fal(e21,λ1,δ1),fal(e22,λ1,δ1), fal(e23,λ1,δ1)]T,λ1、δ1为正常数。 fal函数[7]具体表达式为: (18) 下面对系统的稳定性进行分析,在分析之前首先介绍如下的引理: 1)V为正定函数。 2)存在正实数ε1>0,ε2>0,η∈(0,1)以及一个包含原点的开邻域U0∈U,使得下列条件成立: (19) 则系统状态关于原点有限时间内收敛,收敛时间T依赖于系统初始状态x(0)=x0,满足: (20) 设计如下的李亚普洛夫函数: (21) 对式(21)求导,并将式(15)代入可得: (22) 选取:χ1min=min{k11-ξ11,k12-ξ12,k13-ξ13},k2min= min{k21,k22,k23},则: (23) (24) 根据引理1可知滑模变量s1在有限时间内收敛到原点。 在传统滑模控制中,为了保证系统的鲁棒性,k1的取值较为保守,一般大于外界干扰的上界。文中使用扩张状态观测器,k1选取为大于扩张状态观测器的估计误差即可,减少了k1的值,进而降低控制器输出的抖振。 滑模变量收敛以后,系统运动方程转变为: (25) 对式(25)求导可得: (26) 以攻角通道为例,证明滑模变量收敛后,姿态角跟踪误差在有限时间内收敛。 滑模变量收敛后,攻角通道运动方程为: (27) 式中:αe=α-αd。 构造如下李亚普洛夫函数: (28) 对式(28)求导,并将式(27)代入可得: (29) 且满足: (30) 由引理1可知跟踪误差在滑模面上在有限时间内收敛,收敛时间t1满足: (31) 式中:αets1为滑模变量收敛时的攻角跟踪误差。侧滑角通道与倾斜角通道的误差收敛性分析与攻角通道类似。 针对角速度运动表达式(11),首先设计如下的角速度非奇异终端滑模面: s2=[s21s22s23]T=ωe-ωe0+ (32) 式中:s2∈R3×1;ωe=ω-ωc;ω0为初始姿态角速度误差;γ3、γ4为正对角矩阵,γ3=diag(γ31,γ32,γ33),γ4=diag(γ41,γ42,γ43);0 设计非线性控制律如下: (33) 式中:k3、k4为正对角矩阵,且k3=diag(k31,k32,k33),k4=diag(k41,k42,k43);z4=[z41z42z43]T为干扰Δd的估计值。 假设干扰Δd有界,角速度回路扩张状态观测器的设计如下: (34) 式中:z3∈R3×1为ωc的估计值;b03、b04为正对角矩阵,且b03=diag(b031,b032,b033),b02=diag(b021,b022,b023)。 根据多时间尺度原则,将飞行器姿态控制器分为两个回路进行设计,应保证角速度跟踪误差先收敛,之后角度跟踪误差收敛[9]。因此角速度控制回路的响应速度应该比角度控制回路响应速度快,选取参数时需保证矩阵k4的特征值大于等于k2的特征值的3倍。 将文中提出的自抗扰终端滑模方法应用到高速滑翔飞行器姿态控制模型中,通过MATLAB软件进行仿真实验。飞行器的参数为[10]: (35) 控制器的参数选取如下: k1=diag(0.1 0.1 0.1),k2=diag(2 2 2) k3=diag(0.1 0.1 0.1),k4=diag(6 6 6) γ1=diag(2 2 2),γ2=diag(5 5 5) γ3=diag(2 2 2),γ4=diag(5 5 5) m=n=7/9,h=0.02,r0=1,γ1=γ2=0.8 δ1=δ2=0.1 b01=diag(100 100 100),b02=diag(3 000 3 000 3 000) b03=diag(100 100 100),b04=diag(3 000 3 000 3 000)。 系统初始条件θ0=[0 4.8° 0]T。 1)将文中提出的自抗扰终端滑模(ADRCTSMC)与传统滑模(CSMC)方法相对比,传统的滑模面为: (36) 传统滑模控制律根据指数趋近律的方式设计,即: (37) (38) 式中:k5=diag(0.4 0.4 0.4),k6=diag(2 2 2),k7=diag(5 5 5),k8=diag(6 6 6)。 为减弱虚拟控制指令的抖动,在两种方法的角度控制律中使用如下的边界层函数代替符号函数: (39) 式中:Δ为正实数。 使用饱和函数代替符号函数,在无扰动条件下,滑模变量能够收敛到原点,在有扰动情况下,滑模变量收敛到原点附近的邻域中,邻域的大小与干扰的上界有关。采用文中提出的方法,系统中扰动被有效补偿,保证了使用饱和函数时系统的稳定性。 为验证控制系统的鲁棒性,在第6 s时,系统加入如下干扰来模拟飞行过程中外界的干扰与参数不确定对飞行过程产生的影响。 (40) (41) 系统仿真结果如图2~图8所示。 由图2、图3、图4可以看出:使用两种方法都能够使姿态角跟踪误差收敛,使用传统滑模方法响应过程中超调量较大,不利于飞行器的稳定。使用文中提出的算法,姿态角响应过程超调量较小,且误差收敛较快,协调了系统的快速性与超调量。第6 s系统引入干扰以后,使用传统滑模方法,系统的跟踪值偏离期望值较大,经过一定时间后收敛到期望值。使用自抗扰终端滑模方法,系统控制效果受到的影响较小,姿态角跟踪曲线产生微小波动后立即回到了期望值,系统鲁棒性较强。图5、图6是干扰观测曲线,可以看出:通过使用扩张状态观测器,两个回路的干扰被准确的估计了出来,利用估计值能够有效实现控制器对外界干扰的自适应。对比控制器输出曲线可知,结合自抗扰方法的终端滑模方法可以降低控制增益,在系统稳定后控制器抖振较小。 图2 攻角响应曲线 图3 侧滑角响应曲线 图4 倾斜角响应曲线 图5 角度控制回路干扰观测曲线 图6 角速度控制回路干扰观测曲线 图7 传统滑模控制器输出曲线 图8 自抗扰终端滑模控制器输出曲线 2)在飞行器做大范围机动情况下进行仿真实验,攻角、倾斜角通道指令信号为方波信号,在实际飞行过程中,侧滑角一般保持在0°附近,在第5~10 s与25~35 s间加入式(40)与式(41)所示干扰,仿真结果如图9、图10。 由图9可以看出通过使用自抗扰终端滑模方法,姿态角能够快速地跟踪期望指令,且跟踪过程中超调量较小,满足飞行器做大范围机动的要求,控制器的输出没有明显的抖振。 图9 姿态角响应曲线 图10 自抗扰终端滑模控制器输出曲线 针对高速滑翔飞行器的姿态控制问题,提出了一种自抗扰终端滑模控制方法。首先,给出了高速滑翔飞行器运动模型与姿态控制方程。之后,将自抗扰算法与终端滑模算法相结合,通过微分跟踪器安排过渡过程,将外界的干扰与系统内部的扰动的整体作为总干扰,通过扩张状态观测器对总体干扰进行在线估计。根据终端滑模控制方法设计非线性控制律,对系统的稳性进行了分析并计算了误差的收敛时间。将文中提出的算法应用到高速滑翔飞行器的姿态控制模型中进行仿真验证,并与传统滑模方法进行对比。通过分析姿态角响应曲线可以得出自抗扰终端滑模方法能够兼顾系统的超调量与快速性,系统中的干扰能够被有效的观测出来。飞行器姿态角在有干扰的作用下能较好的跟踪期望值,具有较强的鲁棒性。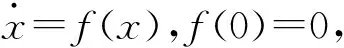
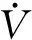
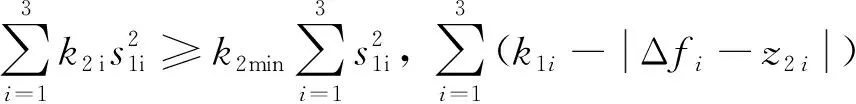
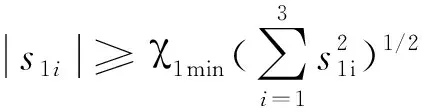
2.2 角速度控制回路自抗扰终端滑模控制器设计
3 数值仿真
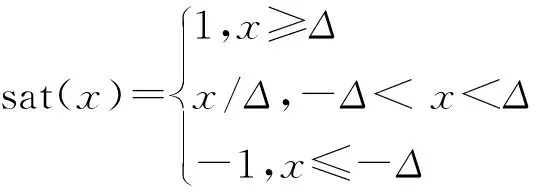

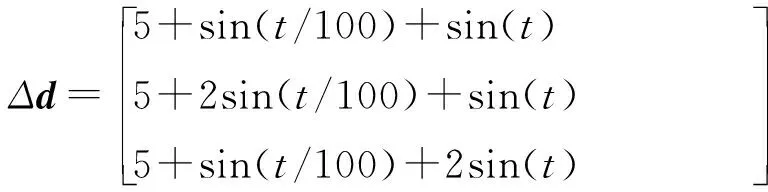

4 总结
