一种多性能要求的控制器设计方法及其应用*

李继广,董彦非,屈高敏,王克平,吴 悦,白楠楠

(西安航空学院飞行器学院, 西安 710077)

0 引言

随着无人机的广泛应用和任务扩展的需求,对无人机的飞行性能也提出了更高的要求[1-2]。这种更高的性能需求,对最常用PID控制方法提出了新的挑战。为了解决该问题,许多现代控制方法得到了重视和深入研究。例如,文献[3]采用根轨迹方法设计PID控制器,实现对可变性飞行器的纵向控制;文献[4]研究了鲁棒H控制综合问题;文献[5]设计无人机姿态自适应模糊PID控制器;文献[6]提出了一种基于约束粒子群优化的导弹控制器设计方法;文献[7]提出了一种最优鲁棒特征结构设计方法。

虽然这些方法相较于传统PID控制方法有着巨大的优势。但是,这些方法设计的目标都是使得控制系统的单一性能指标达到最优。而且,相较于传统的PID控制器,这些方法的设计过程都很复杂,工程实现也很困难。对于无人机这种飞行环境复杂、任务需求多样、自身非线性和耦合特性严重的控制对象来说,单一性能指标最优在实际中并不能满足需要[8-9]。例如,响应特性最优控制器往往稳定性和鲁棒性较差;鲁棒性最优的控制器操作性能和动态特性往往不能令人满意。因此,在工程实践中,需要的并不是单一指标最优的控制器,而是各项指标都能满足需求的控制器。

为了解决该问题,文中在深入分析无人机横侧向运动控制需求的基础上,提出了一种满足多种性能指标约束的控制器设计方法。

1 无人机横侧向运动及控制需求分析

无人机横侧向运动主要包括侧滑角β、滚转角速率p、偏转角速率r及滚转角φ。运动方程如下:

(1)

式中:m为无人机的重量;v0为无人机真空速;δa为副翼;δr为方向舵;Ix、Iz、Ixz为无人机转动惯量；其它为无人机的气动参数。

在无人机的横侧向运动中,侧滑角是需要消除掉的运动状态。从式(1)中的第2、第3式可知,侧滑角对无人机的滚转角和偏航角有着巨大的影响。因此,侧滑角的存在会对无人机的气动特性和稳定性能产生极大的影响,严重影响无人机的飞行性能和飞行品质。滚转角是需要快速、精确控制运动状态,这对无人机的稳定和按航迹自主飞行至关重要。另外,从式(1)中的第1式可知,无人机的滚转角会对侧滑角产生耦合影响。如何在滚转操纵时防止侧滑角的出现是无人机横侧向控制的难点。由于无人机自主飞行的特性,因此对系统的稳定性有着更高的要求。同时,各种扰动和外界干扰,会对无人机的运动产生影响,从而影响飞行稳定和航迹跟踪精度。所以,对控制器的鲁棒性也有较高的要求。

因此,对于无人机的横侧向控制来说,对控制器的要求包括稳定性、快速响应、稳态误差小,以及较强的鲁棒性。这些性能指标并不强调每一项最优,但是要求所有指标都满足控制需求。

2 性能指标的数学表达

无人机横侧向运动模型可表示成如下形式:

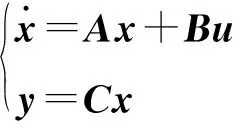
(2)

在满足各种指标需求的控制理论思想指导下,对于带有控制器的闭环系统,建立满足各种系统性能指标需求的约束条件。以原系统式(2)为例,其带有状态反馈的闭环系统为:

(3)

式中:K为状态反馈控制器参数。

该闭环控制系统各项指标以及数学约束如下:

1)极点指标

该指标主要体现系统的稳定性要求和快速响应要求。该指标约束要求闭环系统的极点位于左半复平面区域Ω={s∈C:Re(s)≤-α}(α>0)。该指标约束可用方程表示为[10]:

(4)

2)方差指标

方差指标是系统无稳态误差需求的体现。在数学上,该指标为闭环系统的稳态协方差矩阵E满足diag(E)≤σ2。该指标约束可用方程表示为:

(5)

(6)

设计满足各种需求的控制器,就是求解式(4)～式(6)所确定的线性不等式方程组。

3 基于增广系统的控制器设计

3.1 控制器设计

无人机横侧向线性连续时不变系统可表示为:

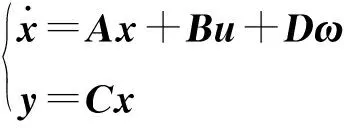
(7)

式中:ω为随机扰动,是均值为零的高斯白噪声,其强度为w>0;A、B、C、D为适维矩阵。

对于式(7)所确定的系统,在控制输入点之前引入积分环节构建增广系统可得:

(8)

式中:

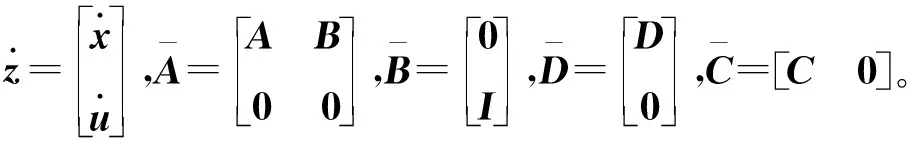
设增广系统的状态反馈为:

uz=Kz

(9)

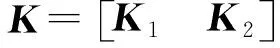
(10)

则可得原系统(7)的PI形式的控制器:

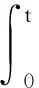
(11)

式中:K3=K2(BTB)-1BT,K4=K1-K2(BTB)-1BTA。

通过式(8)所建立的增广系统,和第2节所确立的性能约束条件,通过求解多维线性矩阵不等式组,则可以得到系统(2)类似传统PI控制器的满足多性能要求的控制器。

3.2 控制器存在性条件

从上节的设计过程知道,无人机横侧向多性能控制器设计最后归结为求解3个线性矩阵不等式。但是,这里面临着一个问题:是否存在这样的反馈控制参数K,使得闭环系统满足这些线性矩阵不等式的约束？

为了回答该问题,文中做如下证明。令X=A+BK为要求解的矩阵,对以上指标约束方程在形式上做简单变形,可以表示成以下统一的形式:

XG+GTXT+Q<0

(12)

下面以确定该线性矩阵不等式方程的可解性条件,从而判断两种控制器可解空间的大小。为了给出线性矩阵不等式(12)具有可行解的条件,先给出下面的投影定理。

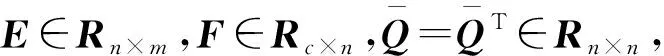
(13)

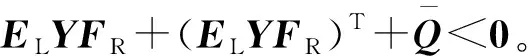
(14)

由Schur补引理,式(14)等价于:

(15a)

(15b)

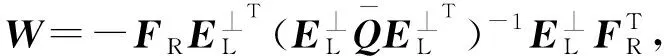
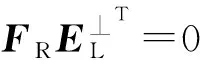
由投影定理可知,式(12)具有可行解的条件是:

GT⊥QGT⊥T>0

(16)

因此,可以得到如下结论:

定理1:线性矩阵不等式XG+GTXT+Q<0可行的充分必要条件为:

GT⊥QGT⊥T>0,XG+GTXT+Q<0

(17)

4 和PID控制器比较

对于文中所得到满足多种性能指标要求的控制器,对原系统来说,实质上是一种类似PI控制器的全状态反馈控制器。那么,该控制器在工程实现上是否存在问题呢？和传统的PID控制器相比又有什么优缺点呢？下面将解决该问题。

4.1 两种控制器性能及结构分析

基于积分环节构建增广系统构建的控制器如式(11)所示。对原系统来说,该控制器实质上是一种全状态反馈控制器。下面分析该控制器的积分部分。

一个系统,在所有激励作用下可表示为:

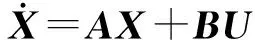
(18)

对上述系统表达式两边积分可得:

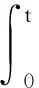
(19)

对于全状态反馈控制系统来说,系统输入可表示为:

U=LX

(20)

把式(20)代入式(19)可得:

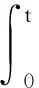
(21)

当矩阵(A-BL)为可逆矩阵时,则有:

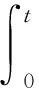
(22)

把式(20)代入式(18)式可得:

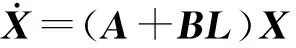
(23)

若系统的比例积分控制器表示为:

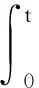
(24)

把式(22)代入式(24)可得:

U=[K3+K4(A-BL)-1]X

(25)

若系统的PID控制器表示为:

(26)

把式(22)和式(23)代入式(26)可得:

U=[K3+K4(A-BL)-1+K5(A+BL)]X

(27)

根据以上分析可知,可得如下结论:

定理2 在系统的状态全部参与控制反馈的情况下,当L=K3+K4(A-BL)-1所确定的矩阵L存在时,全状态反馈控制器与比例积分(PI)控制器等价。当L=K3+K4(A-BL)-1+K5(A+BL)所确定的矩阵L存在时,全状态反馈控制器与PID控制器等价。

4.2 文中控制器的优点

工程实践中,在控制性能相当的情况下,文中控制器在结构和工程应用上具有的优势如下:

首先,设计得到的控制器和传统PID控制器相似,具有结构简单的优点。另外,由定理2可知,该控制器在满足一定条件下,和传统PID控制等价。但是,由于采用了全状态反馈控制的形式,相当于对系统的每一状态都进行了控制。因此,相较于只对输出状态进行控制的传统PID控制器来说,可以获得更好的控制效果。

第二,减少了控制对微分和积分信号的依赖,方便工程实现。以飞行控制系统为例,在当前技术条件下可以直接测量得到的反馈信号依然有限。迎角、侧滑角等信号的测量误差较大,测量仪器安装困难且传感器成本较大;积分和微分等高阶信号直接测量是十分困难甚至是不可能的。因此,减少对微分和积分信号依赖的控制器,更利于工程实现。

第三，提高系统的可靠性。全状态反馈控制器可以不必测量系统的微分和积分信号,减少了系统大测量和电子器件。在器件故障率相同的条件下,减少器件的使用数量,也就提高了系统的可靠性。

第四,经济性更好。测量敏感器件的花销占据了控制系统成本的很大一部分,全状态反馈控制器依赖比较少的反馈信号,降低了系统中测量敏感器件的数量,从而降低了控制系统的成本。

5 仿真验证

某飞机的飞行状态为:飞行速度v0=100 m/s,H=5 000 m。侧向运动方程为:

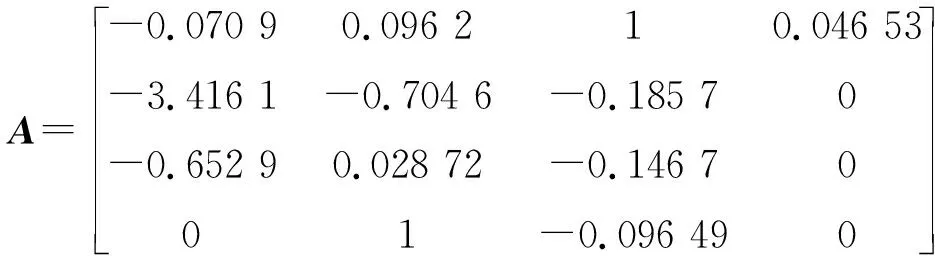
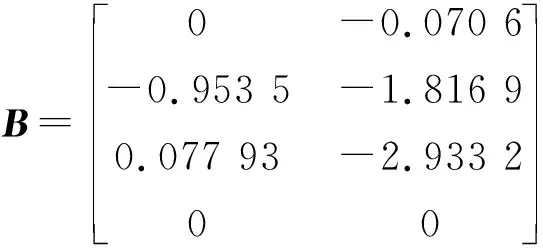
以极点位于(-6,0)为圆心,2为半径的圆形区域,方差指标σ≤10为设计条件,采用满足多性能要求的控制器设计方法得到的控制器参数如下:

采用设计得到的控制器,下面来验证控制器的控制效果。首先来看控制器对侧滑角的消除能力。当侧滑角为5°时,无人机的侧滑角响应如图1所示。

图1 控制器对无人机侧滑角的消除能力

从图1可知,控制器仅用了2 s就消除了无人机的侧滑角,响应迅速。而且,侧滑角收敛到0°状态,没有稳态误差的存在。说明文中所设计的控制器具有快速消除侧滑角的能力。

接下来看控制器对滚转角通道的快速响应能力。给定5°滚转角指令,无人机的滚转角响应如图2所示。

从图2可知,无人机的滚转角仅用1.8 s就快速跟踪了滚转角输入指令。而且响应过程无超调、无稳态误差。

从无人机侧滑角消除和滚转角响应仿真结果可知,所设计的控制器具有良好的性能,满足设计要求。证明了文中方法所设计的控制器是有效的。

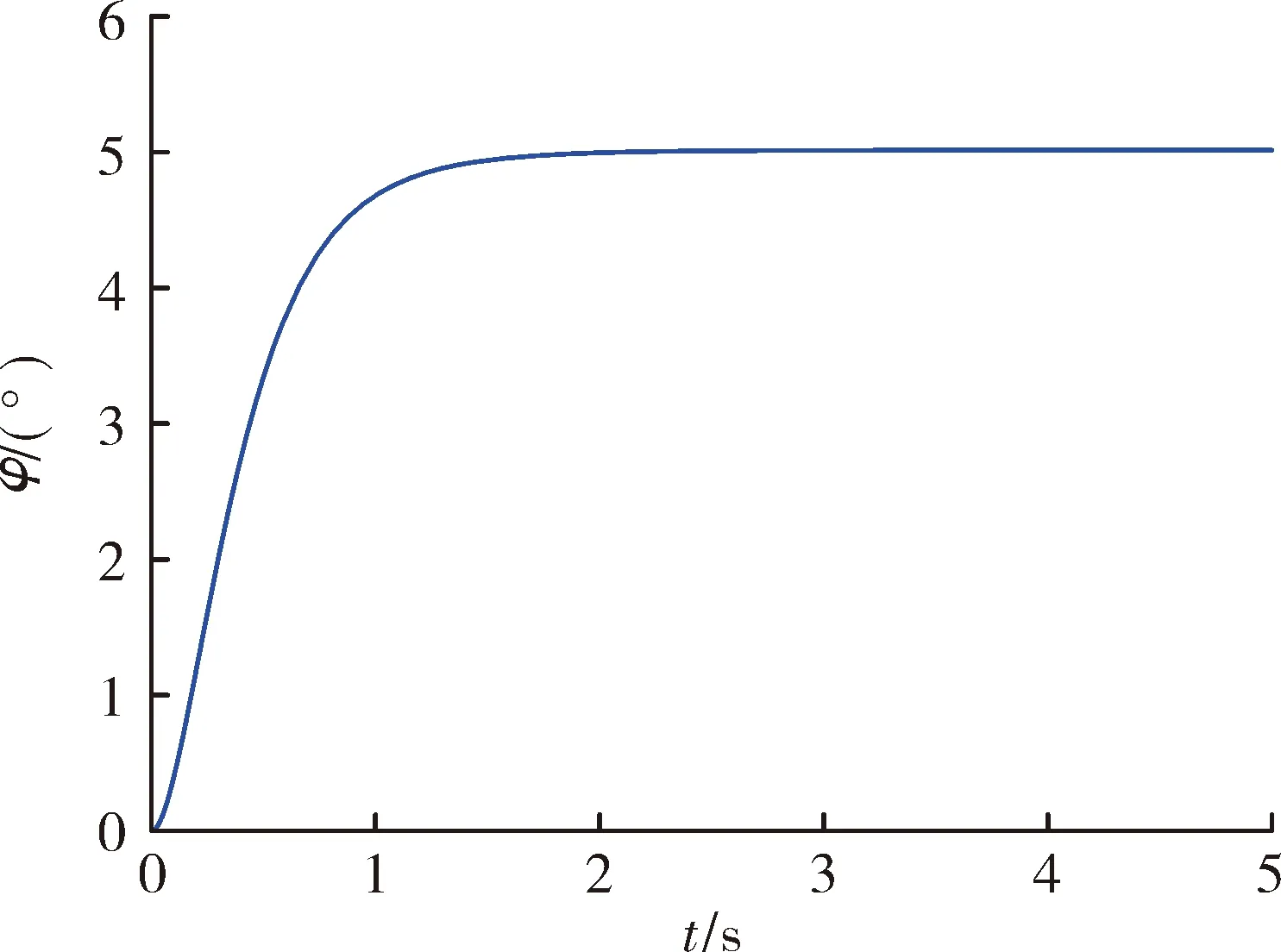
图2 无人机滚转角通道响应

6 结论

针对无人机横侧向控制的具体问题和工程上对控制器的实际需求,提出了一种满足多性能需求要求的控制器设计方法。工程所需要的控制器,并不追求单一性能指标的最优,而是各项性能指标都满足需求。因此,文中以稳定性、快速响应、稳态误差、鲁棒性为设计性能指标要求,设计一种满足多种性能要求的控制器。文提出了该控制器的设计步骤,证明了该控制器存在的条件,以及该控制器和传统PID控制器对比存在的优点。

所设计控制器的优点包括:控制效果好;减少了控制器对微分和积分信号的依赖;提高系统的可靠性;经济性更好。最后,通过对无人机横侧向运动控制器的设计和仿真验证,证明了该控制器满足各种性能指标,该方法是有效的。