二阶多智能体系统的量化迭代学习控制*

丁斗建,赵晓林,赵博欣,高关根,刘 畅

(1 空军工程大学研究生院, 西安 710051;2 空军工程大学装备管理与无人机工程学院, 西安 710051; 3 中航工业西安飞行自动控制研究所惯性技术航空科技重点实验室, 西安 710065)

0 引言

近年来,多智能体系统得到了广泛的研究和发展,先后被学者应用到机器人编队,无人机集群等领域[1-2]。其中一致性问题是多智能体系统研究的热点方向,目的是通过设计一定的控制序列,使每个智能体在信息交流后实现同步。通过智能体之间的协同和合作,可以提高系统的容错率、鲁棒性以及稳定性,能较好解决复杂问题,是单个智能体不能企及的。

随着对多智能体系统一致性问题研究的不断深入,相应的研究成果不断出现。文献[3]考虑了信息受限下二阶多智能体系统一致性问题;文献[4]为了解决多智能体系统一致性跟踪问题,提出了一种分布式自适应控制协议;文献[5]则提出了一种异质控制协议,用于多智能体系统自适应跟踪。相比于以上研究成果,文献[6]考虑了分数阶不确定多智能体系统,在设计控制协议时,结合了状态观测器。

迭代学习控制方法,是一种基于重复学习的思想,不断重复有限时间内的操作,以到达改善控制效果的学习方法。文献[7-10]应用迭代学习控制方法,实现了多智能体系统的编队控制,同时还针对此方法,研究了有限时间输出一致性问题;文献[11-12]从迭代学习控制算法的初始条件出发,提出了分布式初始状态学习控制方法,研究了多智能体系统的一致性问题;文献[13-14]研究了迭代学习控制下多智能体系统一致性跟踪问题。

近年来,有学者为了解决多智能体系统中数据传输带来的负担问题,引入了量化控制。所谓量化控制,就是将系统的实际连续信号转化为分段连续信号再进行传输的一种数据处理方法。文献[15]针对一类非线性二阶多智能体系统,引入了均匀量化控制,研究了有领导智能体时系统的跟踪问题;文献[16]研究了二阶多智能体系统在有向拓扑图结构下,结合概率量化方法设计了控制协议,实现了系统的一致性;文献[17]考虑了一阶多智能体系统量化迭代学习控制下的一致性实现问题。

针对以上分析不难发现,量化控制方法,已经被大量用于多智能体系统中,以解决相应的问题,如跟踪、同步等,也有学者将量化控制方法与迭代学习控制方法结合,提出了基于量化的迭代学习控制协议,如文献[17]。文献[17]仅考虑了一阶多智能体系统的情形,文献[16]虽然对二阶多智能体系统引入了量化器,但并没有结合迭代学习控制,而且对于带有领导智能体的多智能体系统的情况也没有考虑。

综合以上分析,考虑到迭代学习方法对控制目标的修正效果,以及量化器的引入能降低信号在链路传输中的负担等原因,文中针对带有领导者的二阶多智能体系统,引入量化器,并结合迭代学习控制方法,设计量化迭代学习控制协议。具体实施过程为:给定多智能体系统,对系统的状态误差和状态两类情形分别进行量化,应用量化后的结果,结合迭代学习控制方法,设计基于量化信息的迭代学习控制协议,再将所设计的控制协议,作用于给定系统并分析控制效果。

1 预备知识

1.1 代数图论基本知识

对于由n个节点组成的无向图G=(V,E,A),定义V={1,2,…,n}是点集,E∈{(i,j):i∈V,j∈V}是边集,A=[aij]n×n,aij∈R是图的连接权值矩阵,邻居集Ni表示所有的信息由节点j流向节点i的集合。对于任意两个不同的节点,如果i,j∈V,有aij=aji≥0,当j∈Ni时,有aij>0,定义aii=0,di=∑j∈Niaij,D=diag{d1,d2,…,dn},那么图的拉普拉斯矩阵可以表示为L=D-A。对于无向图G,权值矩阵A是对称的,同时,如果图中任意两点存在一条路径,则此无向图是连通的。

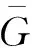
1.2 对数量化器

考虑对数量化器[18-19],取量化等级U={±ui:ui=ρiu0,i=0,±1,±2,…}∪{0}。其中,u0>0;ρ∈(0,1)是量化密度。量化器Q(·)由式(1)给出。

(1)

式中:δ=(1-ρ)/(1+ρ)。显然,由式(1)所定义的量化器Q(·)为对称且时不变的,其量化结果是将实际输入转化为分段连续输出。不同量化密度下的量化输出如图1所示。

图1 不同量化密度下的量化输出

根据文献[19],对于给定的量化密度ρ,对数量化器具有如下的性质:

Q(x)-x=Δ·x

(2)

式中:x表示量化器的输入,Δ·x表示量化误差,且‖Δ‖≤δ。

定义1对于给定的向量函数f(t):[0,T]→Rn的λ范数定义为:

(3)

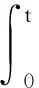
(4)

特别的,当a=0时,有

(5)

式中:‖·‖λ表示λ范数。

定义3Rn表示n×1阶列矩阵,Y=[1,1,…,1]T表示元素全是1的列向量。

2 主要结果

2.1 问题描述

考虑由n个智能体和1个领导者组成的二阶多智能体系统,其中第i个智能体在第k次迭代时的动态方程表示为:

(6)

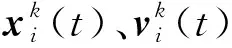
假设领导者的动态方程表示为

(7)

式中:x0(t)、v0(t)和u0(t)分别表示领导者的位置、速度和控制输入。

则可以定义多智能体系统一致性误差为:

(8)

2.2 基于量化状态误差的一致性

在这一节中,主要对系统状态误差进行量化。考虑给定的系统式(6)和式(7),在信号传输的过程中,引入对数量化器。设计第i个智能体的量化一致性误差为

(9)

式中:aij是连接矩阵A中的元素;bi表示智能体i与领导者相连的连接权值;Q(·)表示对系统状态误差的量化输出。

根据对数量化器的性质式(2),将式(9)转化为

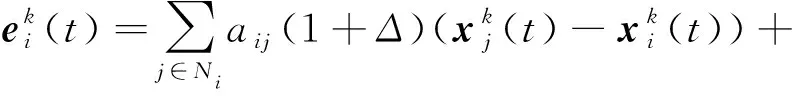
(10)

将上式写成矩阵的形式：

(11)

将式(8)写成矩阵的形式,则有:

(12)

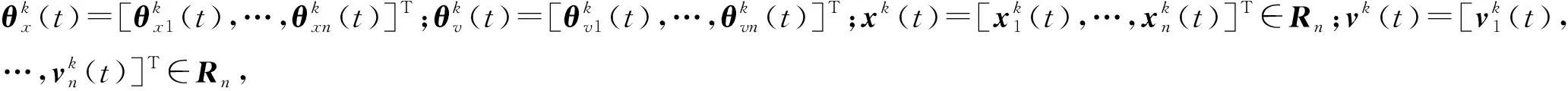
(13)

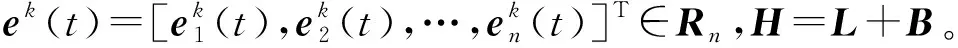
根据迭代学习控制思想,设计迭代控制协议:

(14)

式中:uk(t)∈Rn是智能体在第k代的控制输入,Γ是学习增益矩阵。

将式(13)代入式(14),则有:

(15)

设计如下初始学习协议:

(16)

从迭代学习控制的观点考虑,控制协议式(15)以及初始条件式(16)可以看作是微分型迭代控制序列。结合式(12)可知,这种迭代控制协议主要利用邻居智能体间的误差信息进行交流,因此具备了迭代学习控制和分布式协议的特点。

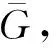
证明根据多智能体系统动态方程(6),不难发现

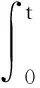
(17)

将式(15)代入式(17),则有

(18)

对式(18)右边积分得：

(19)

代入初始条件式(16),有

(20)

根据式(12),式(20)可以转化为：

(21)

进而,有

(22)

对上式两边同时积分,即

(23)

则有

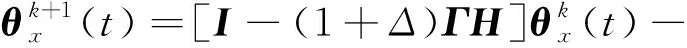
(24)

代入初始条件(16),式(24)可以转化为:

(25)

对上式两边同时取范数,则有

(26)

用e-λt乘以式(26)的两边,并根据定义1和定义2,则

(27)

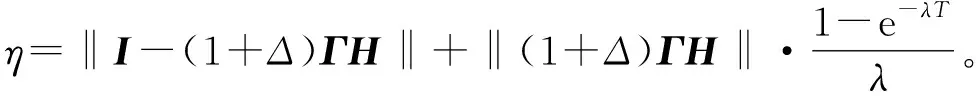
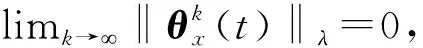
2.3 基于量化状态的一致性

这一节,主要考虑的是对系统状态进行量化。设计第i个智能体的量化一致性误差为:

(28)

结合对数量化器的性质,类似于2.2节的分析,可以得到:

(29)

式中:H′=D+B。设计迭代控制协议

(30)

将式(29)代入式(30),得

(31)

设计如下初始学习协议

(32)

证明因为

(33)

代入初始条件式(32),式(33)可化为:

(34)

结合式(12),式(34)可化为:

(35)

对上式两边同时积分,并代入初始条件(32),得:

(36)

对上式两边同时取范数,则有

(37)

用e-λt乘以式(37)两边,根据定义1和定义2,有

(38)

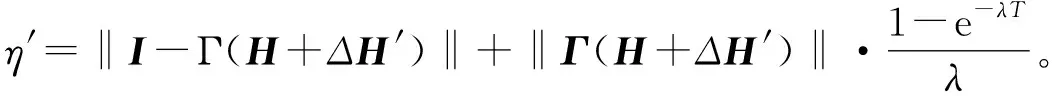
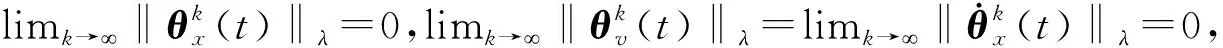
对于固定的多智能体系统拓扑图,H和H′是固定的,可以选择合适的学习增益矩阵Γ和量化密度ρ,使条件‖I-(1+Δ)ΓH‖<1和‖I-Γ(H+ΔH′)‖<1满足控制要求。

3 仿真分析

为了验证文中结论的正确性,对上节所述两种情形进行仿真分析。考虑5个智能体和1个领导者组成的多智能体系统,其无向拓扑图如图2所示,0号代表领导者。

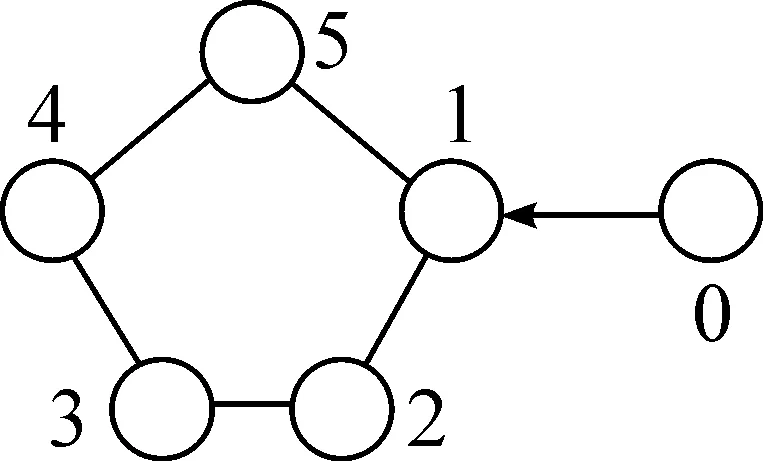
图2 多智能体系统通讯拓扑图

根据第2章所介绍的基本知识,可以得到：

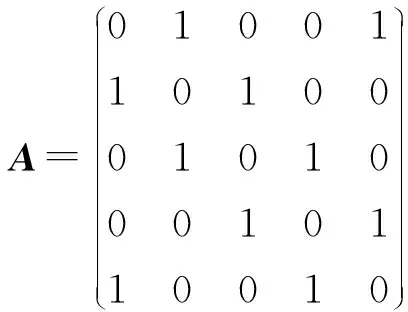
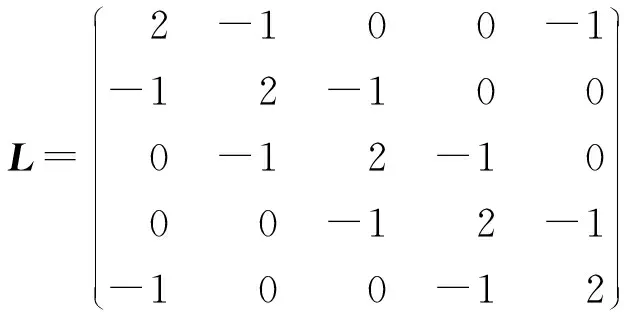
B=diag(1,0,0,0,0),D=diag(2,2,2,2,2)

情形1考虑量化系统状态误差

给定每个智能体动态方程如式(6),领导者动态方程如式(7),领导者的输入为,u0(t)=sin(t)。

设多智能体初始位置和速度分别为x1(0)=[2,2.5,1.5,1,0.5]T和v1(0)=[1.5,-1,0.5,-0.5,1]T;领导者初始位置,x(0)=[0,0,0,0,0]T,v(0)=[0,0,0, 0,0]T,仿真时间设置为t∈[0,6 s]。选取量化密度ρ=0.35,则σ=0.481 5,所以Δ∈[-0.481 5,0.481 5],这里选择Δ=-0.45。

选择Γ=diag[0.25,0.25,0.25,0.25,0.25],则有‖I-(1+Δ)ΓH‖=0.963 2<1,满足定理1要求。取迭代次数k=200,考虑迭代学习控制律(15)和初始状态更新控制律(16),仿真结果如图3～图6所示。

图3和图4是5个智能体的位置和速度跟踪结果。由图可以看出,随着迭代次数的增加,最终初始状态逐渐趋近于领导者的初始状态,多智能体实现对领导者的跟踪。图5是k=200时的控制输出,可以看出,最终每个智能体的控制近乎一致,从而说明了多智能体的状态将不再发生改变。图6是200次迭代过程中最大位置和速度误差绝对值的变化曲线。最终误差趋近于0,从而表明了定理1的有效性。

情形2考虑量化系统状态

令多智能体系统和领导者动态方程与情形1保持一致。设多智能体初始位置和速度分别为x1(0)=[2,1.7,2.5,1.5,1],v1(0)=[1.5,2,2.5,1.7,1.5]T,其它参数设置与情形1一致。这里选择Δ=0.35。选择Γ=diag[0.35,0.35,0.35,0.35,0.35],则有‖I-Γ(H+ΔH′)‖=0.761 7<1,满足定理2的要求。取迭代次数k=50。考虑迭代学习控制律(31)和初始状态更新控制律(32),仿真结果如图7～图10所示。

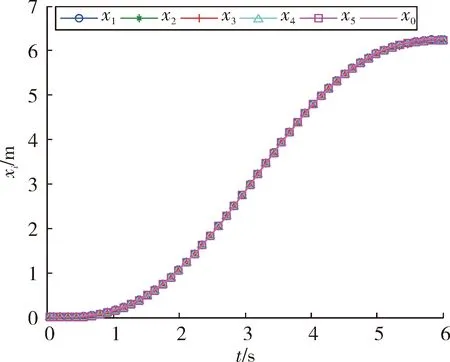
图3 5个跟随智能体放入位置跟踪结果

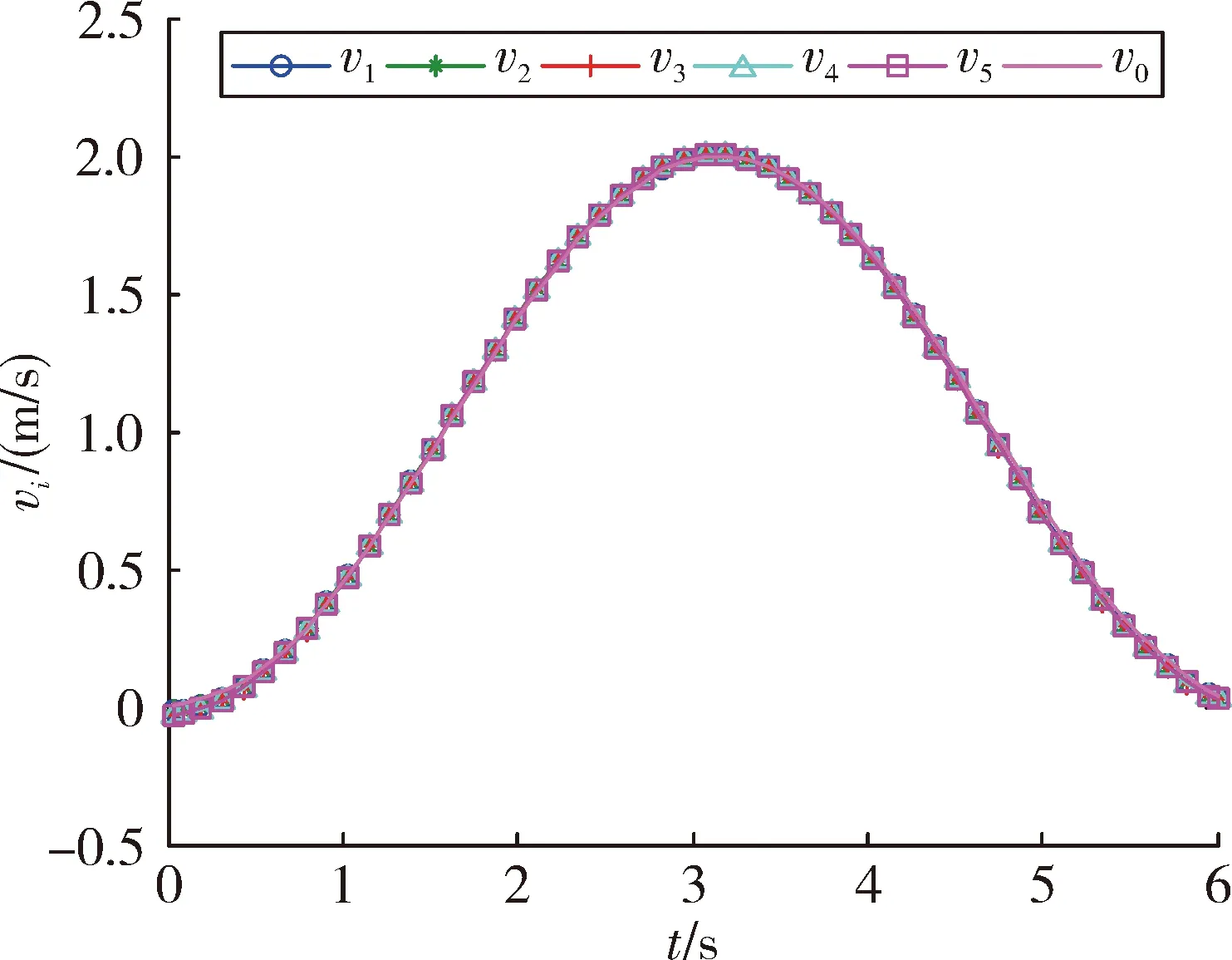
图4 5个跟随智能体放入速度跟踪结果

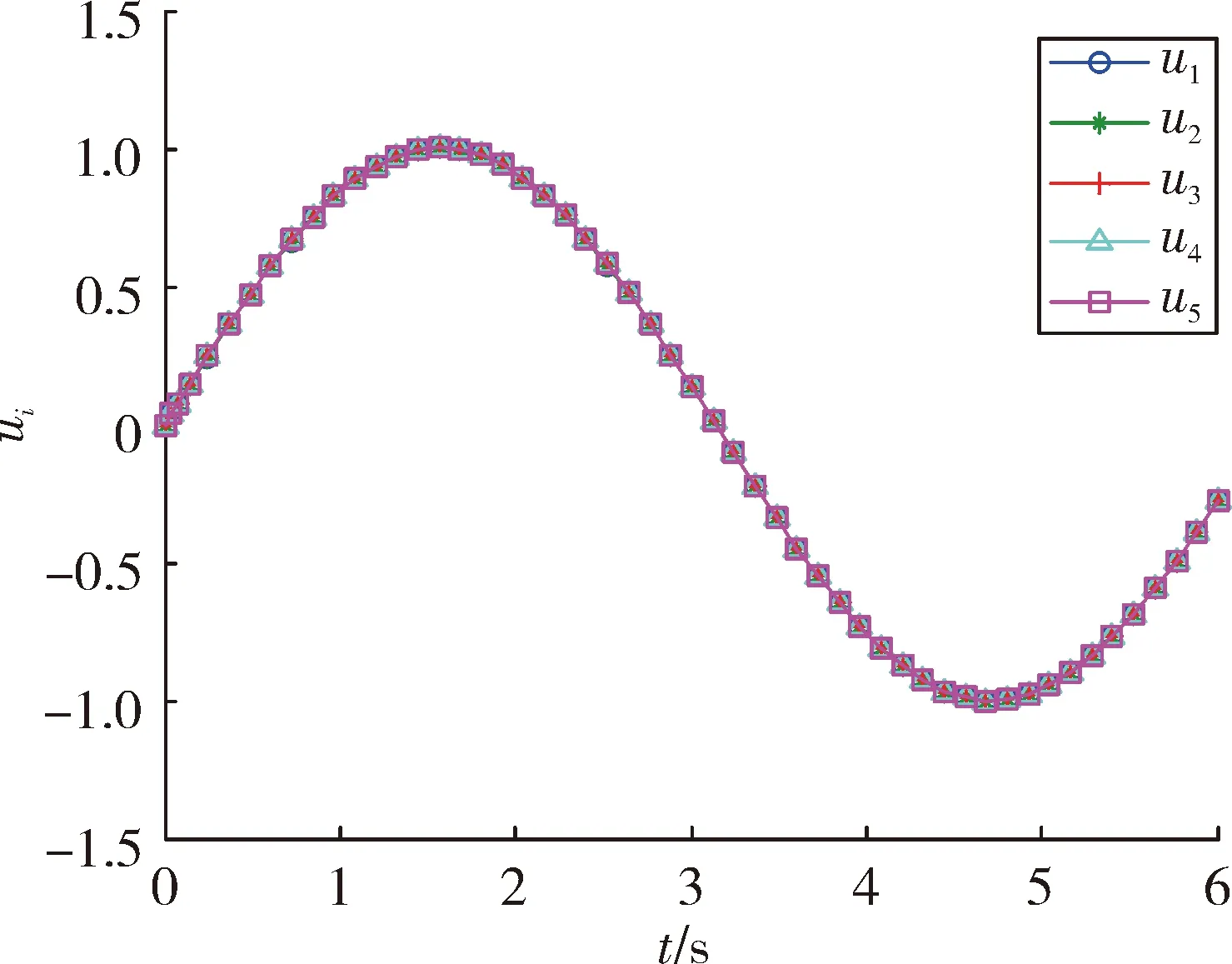
图5 k=200时的控制输出

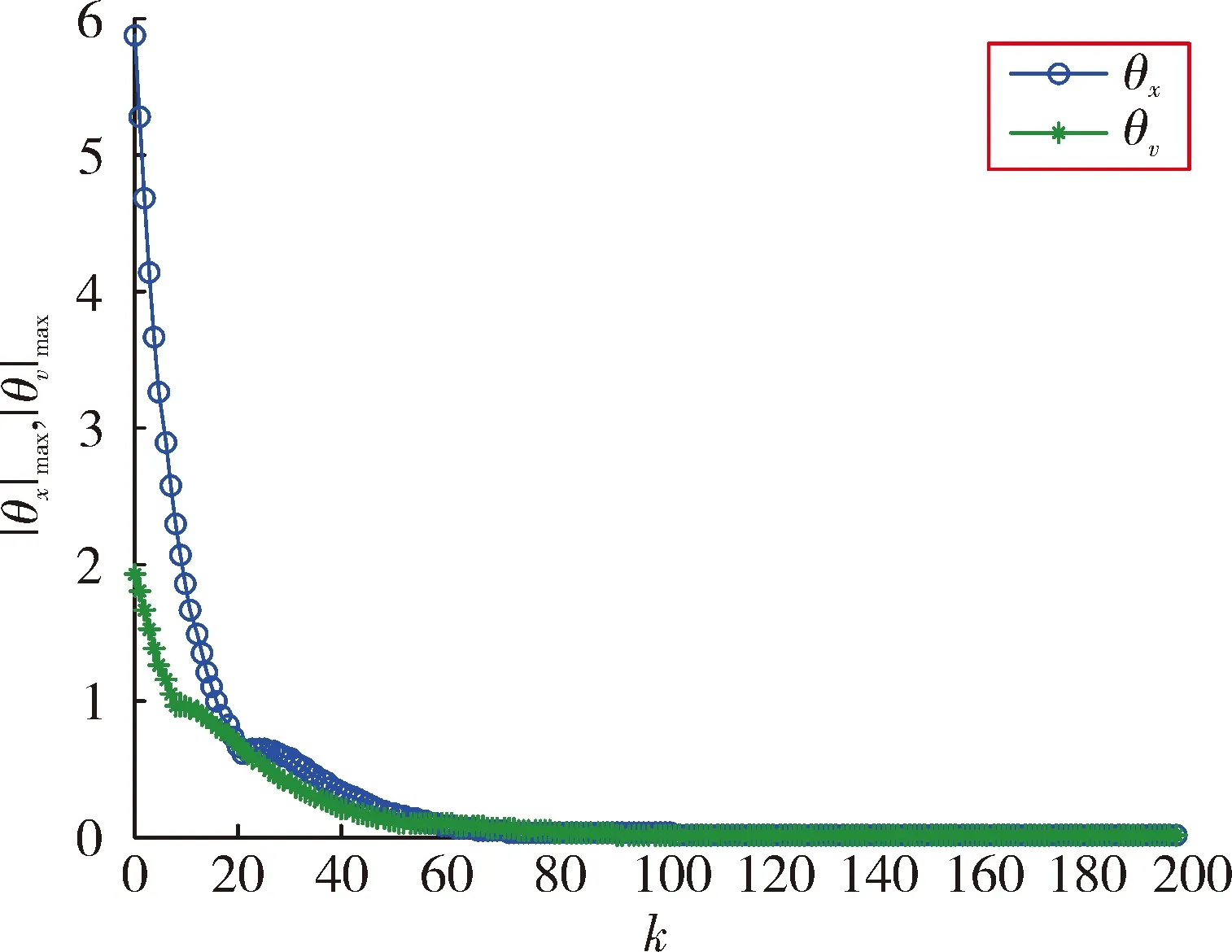
图6 最大位置和速度跟踪误差

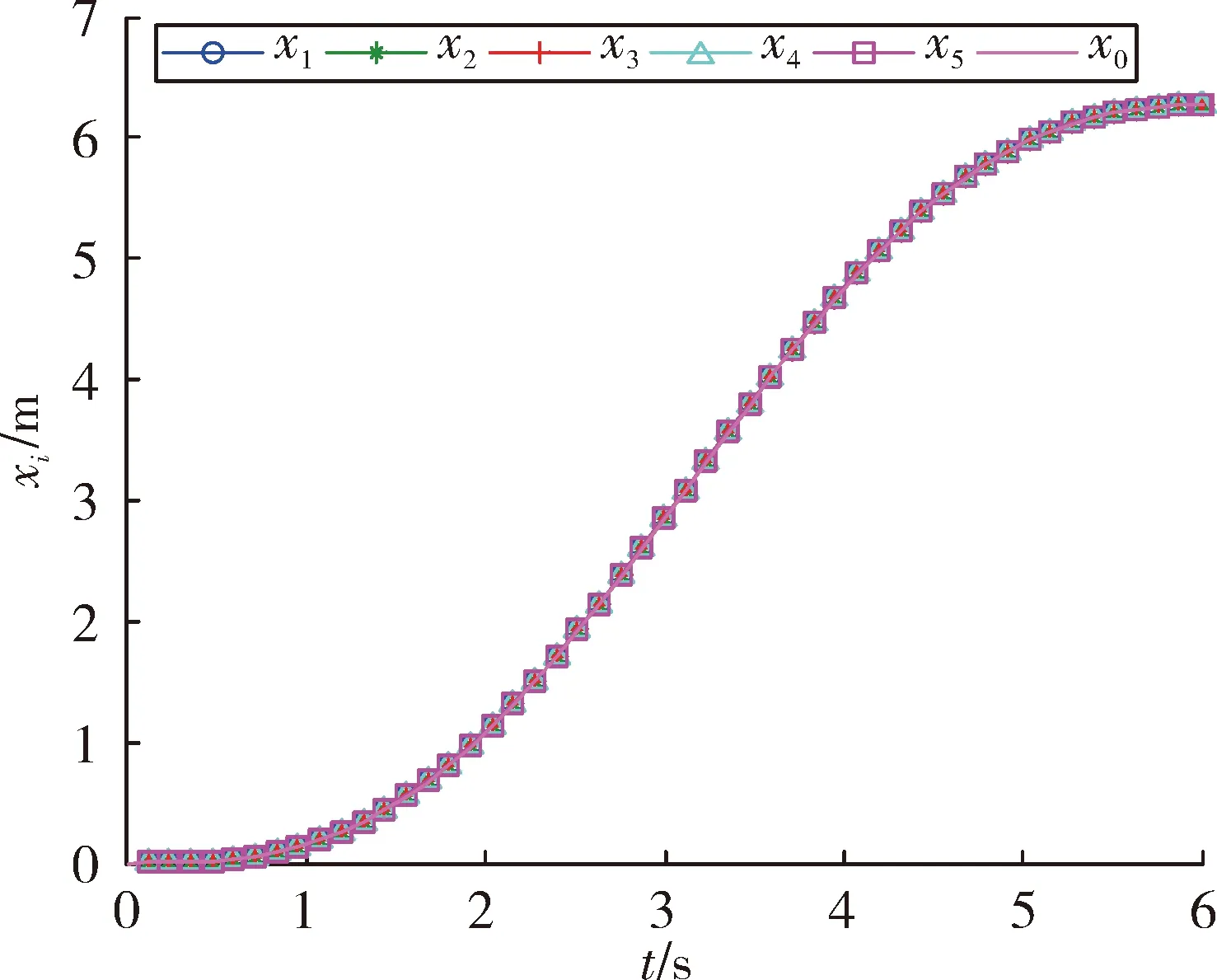
图7 5个跟随智能体放入位置跟踪结果

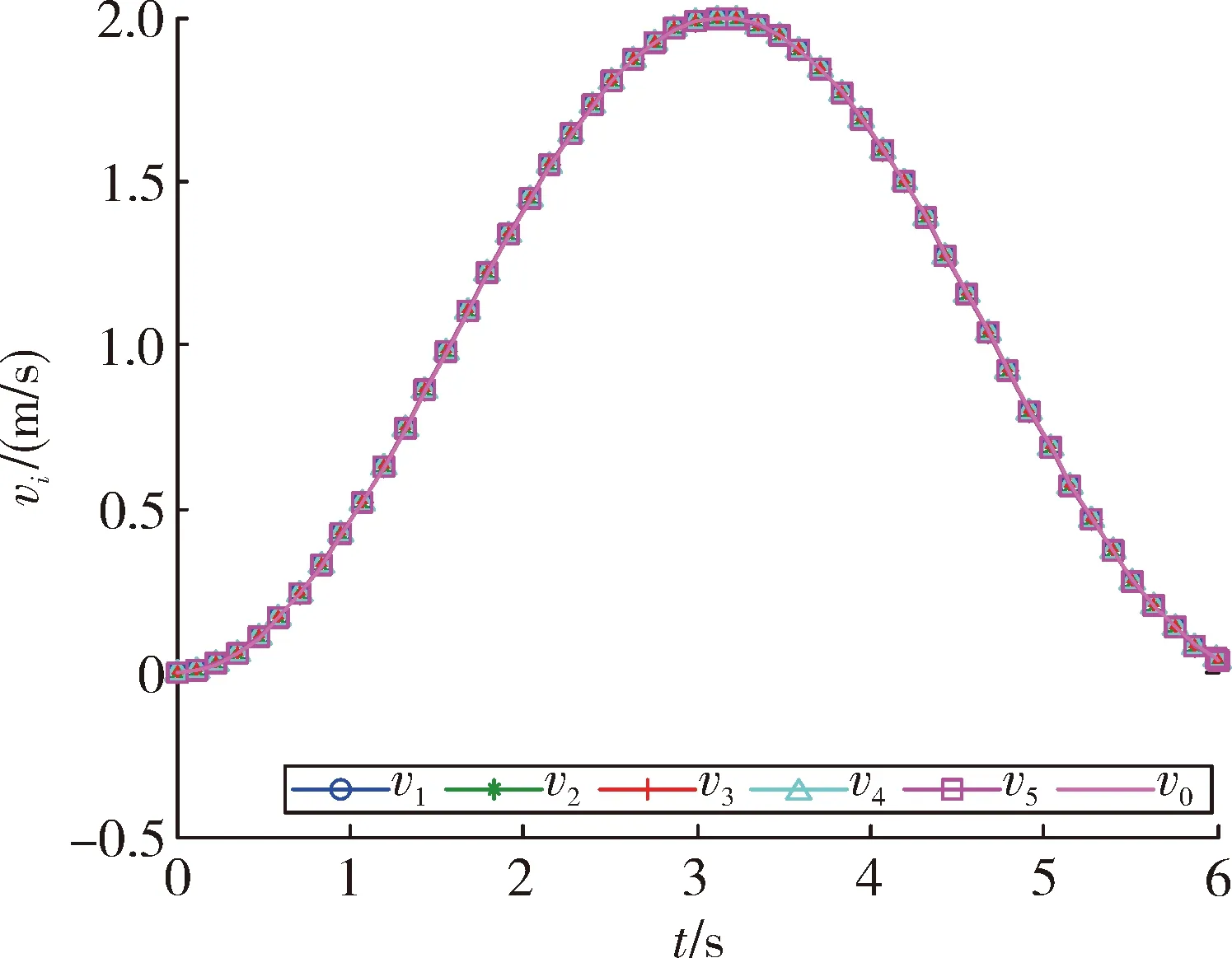
图8 5个跟随智能体放入速度跟踪结果

图9 k=50时的控制输出

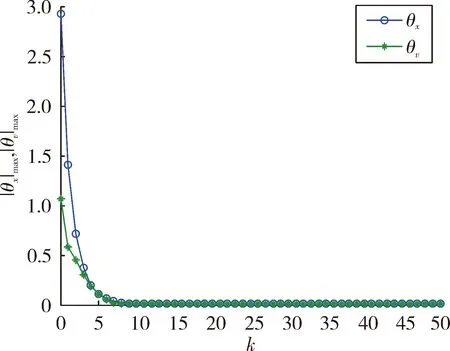
图10 最大位置和速度跟踪误差

图7和图8是5个智能体的位置和速度跟踪结果。由图可以看出,随着迭代次数的增加,最终初始状态逐渐趋近于领导者的初始状态,多智能体实现对领导者的跟踪;图9是k=50时的控制输出,可以看出,最终每个智能体的控制几乎一致,从而表明了多智能体系统的状态将不再发生改变;图10是50次迭代过程中最大位置和速度误差绝对值的变化曲线,最终误差为0,从而表明了定理2的有效性。

图3和图4,图7和图8的结果说明,虽然多智能体的初始位置与领导智能体的不同,但是随着迭代次数的增加,最终实现了同步;相比文献[7]和文献[14]要求多智能体的初始位置与领导者一致,对条件进行了放宽;与情形1相比,情形2实现对领导者的跟踪,所需迭代次数明显较少,这是因为‖Δ‖选取不一样,情形2要比情形1粗糙。

4 结论

文中应用量化器信息,结合迭代学习控制方法,分析了基于量化系统状态误差和量化系统状态两种情形下的带有领导者的二阶多智能体系统一致性实现问题;针对不同情形,设计了不同的迭代学习控制协议和初始状态更新律,通过理论分析,获得了智能体实现对领导者跟踪同步的收敛条件,仿真结果表明了所设计的量化迭代学习协议的有效性。后续工作将在此基础上对高阶多智能体系统进行相关分析和讨论。