顾及系统间偏差的BDS/GPS单钟差定位法

王彦恒,潘树国，喻国荣，张 建

(1.东南大学 仪器科学与工程学院，江苏 南京 210096；2.东南大学 交通学院，江苏 南京 210096)

目前，多GNSS(Global Navigation Satellite System)伪距单点定位已广泛应用于导航领域，但是，由于各系统接收机端硬件延迟不一致且难以与接收机钟差分离[1-2]，导致即使采用同一个接收机时钟，对每个系统单独考虑接收机钟差项(本文称之为传统方法)，使得冗余观测量减少，数学模型强度降低，尤其在遮挡环境下，即使多系统存在因卫星过少参数过多而导致定位结果不可靠的问题。一个典型的情况就是当某个系统只观测到1颗卫星时，由于吸收接收机端硬件延迟的接收机钟差参数的存在，该系统并未提供冗余观测信息[3]。而目前处于大众消费水平的导航设备均采用传统方法进行定位解算。

为了得到系统间偏差(ISB，Inter-System Bias)信息，需估计一个接收机钟差参数(本文称之为单钟差模型)，增加冗余观测量，提高数学模型强度。但是，在导航中，从外部机构实时获取所用设备的ISB信息比较困难，因此，需要依赖接收机硬件延迟的时域变化特性进行实时处理。

文献[1]指出GPS硬件延迟较为稳定，对于与时间存在系统相关的硬件延迟，可采用简单的线性模型进行逼近。文献[4-7]的研究结果表明，GPS系统接收机端硬件延迟具有短期时域稳定性，日稳定度可优于1 ns。文献[8-10]指出，北斗系统接收机端硬件延迟同样具有时域稳定性。而对于BDS/GPS系统间偏差，理论上应处于短期稳定状态，但是系统之间的相互影响可能会破坏稳定状态；有学者研究表明，BDS/GPS系统间偏差同样处于短期稳定状态。文献[3]利用BDS/GPS系统间偏差的时域稳定特性，进行BDS/GPS双系统紧组合载波差分定位，结果表明，这种方式可以显著增强遮挡环境下的定位精度与可用性，但是其采用的载波差分形式并不适用于目前普遍基于伪距进行定位的导航型终端。

利用ISB的时域稳定特性，在卫星数足够的情况下，实时估计每个系统含有硬件延迟的接收机钟差，从而获得ISB信息，当进入遮挡环境，卫星数过少时，将已获得的ISB信息当作已知量，从而减少待估参数，增加冗余观测信息，增强数学模型强度，提高定位精度与可靠性，同时可以降低矩阵求逆维数，减少计算量。

基于目前导航终端所存在的不足与ISB的时域稳定性，本文提出单钟差模型定位算法。采用实测数据验证BDS/GPS双系统在开阔环境及遮挡环境下单钟差模型算法的可用性，并与传统方法进行对比。

1 单钟差模型及算法

BDS与GPS伪距观测方程：

(1)

(2)

式中：P为伪距观测值，上标s为卫星，下标B与G分别为BDS与GPS，下标r为接收机，ρ为站星距，T为对流层延迟，I为电离层延迟，dt为钟差，hd为硬件延迟，ε为观测噪声。卫星钟差与卫星端硬件延迟采用广播星历中的参数进行改正。

从式(1)与式(2)可以看出，若BDS与GPS共用同一个接收机时钟，则只含有一个接收机钟差项，但是由于接收机硬件延迟与接收机钟差线性相关，难以分离，因此在传统方法中，对BDS与GPS各引入一个接收钟差参数，用以吸收硬件延迟，则式(1)与式(2)变形后：

(3)

(4)

其中：

dtr,B=dtr+hdr,B,dtr,G=dtr+hdr,G.

设共观测到m颗BDS卫星与n颗GPS卫星，则误差方程组：

(5)

式中：v为观测值残差；l,q,w为方向余弦；f为观测信息；X,Y,Z为位置参数。假设事先获得了BDS/GPS接收机端的ISB信息ISBB,G，ISBB,G计算方式：

ISBB,G=hdr,G-hdr,B=dtr,G-dtr,B，

(6)

联合式(4)与式(6)可得：

(7)

则根据式(3)与式(7)所得误差方程组：

(8)

比较式(5)与式(8)可知，在BDS/GPS双系伪距单点定位中，若事先获得接收机端的ISBB,G，则可减少一个接收机钟差参数，提高数学模型强度。实际应用中从外部机构实时获取所用设备的ISBB,G比较困难，但是可以利用ISBB,G的时域稳定特性，在卫星数足够的情况下，采用传统方法对BDS与GPS各估计一个接收机钟差，按照式(6)得到ISBB,G，当卫星数较少时，将ISBB,G作为已知信息带入观测方程组，从而减少参数个数，提高数学模型强度。

2 实验验证与讨论

采用两组数据对单钟差模型算法进行验证，一组采用TrimbleNetR9数据，另一组采用UBLOX M8T数据，两组数据信息如表1所示。

表1 实验数据信息表

2.1 系统间偏差计算与分析

在进行单钟差模型定位之前，首先分析在实验数据时长内ISBB,G的时域稳定特性。先利用传统方法估计BDS与GPS接收机钟差，再利用式(6)计算ISBB,G，所得ISBB,G如图1所示，图1(a)与图1(c)分别表示Trimble NetR9ISBB,G与ISBB,G的历元间差分ΔISBB,G(t,t+1)(其中，ΔISBB,G(t,t+1)=ISBB,G(t+1)-ISBB,G(t))的变化趋势，图1(b)与图1(d)分别表示UBLOX M8T的ISBB,G与ΔISBB,G(t,t+1)的变化趋势，统计结果如表2所示。

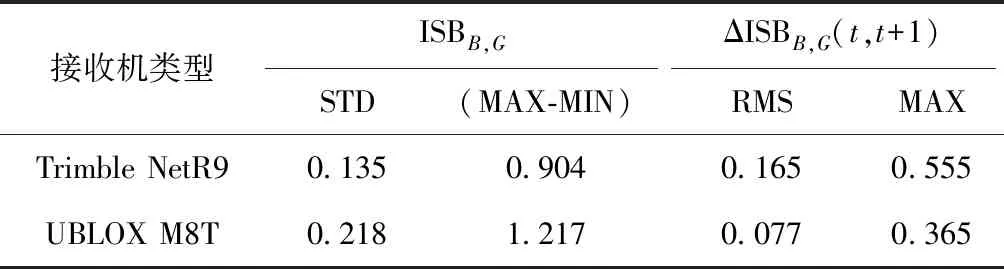
表2 BDS/GPS系统间偏差统计表 m

注：表中ΔISBB,G(t,t+1)的MAX值采用绝对值计算

从图1(a)与图1(c)可以看出，Trimble NetR9在100 min内ISBB,G处于稳定状态，从表2统计结果可以看出，ISBB,G稳定度为0.135 m，最大最小差为0.904 m，ΔISBB,G(t,t+1)RMS为0.077 m，历元间差值最大为0.555 m，对于伪距单点定位米级定位精度而言，能够保证在数分钟之内将利用传统方法获得的ISBB,G作为已知信息进行单钟差模型解算而并不明显损失定位精度。

但是，Trimble NetR9接收机成本高，难以进入大众导航领域，因此本文又选取成本较低的UBLOX M8T接收机进行实验，其ISBB,G与ΔISBB,G(t,t+1)如图1(b)与图1(d)所示，统计结果如表2所示，综合图1(b)、图1(d)与表2，UBLOX M8T接收机ISBB,G在100 min内较为稳定，稳定度为0.218 m，最大最小差为1.217 m，ΔISBB,G(t,t+1)的RMS为0.077 m，最大为0.365 m，同样能够保证在数分钟之内将利用传统方法获得的ISBB,G作为已知信息进行单钟差模型解算而并不明显损失定位精度。

2.2 单钟差模型验证与分析

对ISBB,G时域稳定特性进行了分析之后，利用上述两组数据对单钟差模型定位效果进行验证。在单钟差模型定位中，每隔5 min利用传统方法对ISBB,G进行更新；截止高度角分别设置为10°，30°，50°，其中30°和50°用来模拟遮挡环境；在对ISBB,G进行更新时刻，将截止高度角设置为10°。定位结果如图2与图3所示，图2表示Trimble NetR9，图3表示UBLOX M8T。从左至右依次为传统方法定位偏差、单钟差模型定位偏差、卫星数，从上至下依次为截止高度角10°，30°，50°。统计结果如表3所示。

图2 Trimble NetR9定位偏差

表3 定位结果对比统计表

从图2、图3及表3可以看出，在截止高度角分别为10°与30°时，单钟差模型略低于传统方法，这是因为卫星数足够多，卫星几何分布较好。当截止高度角提高到50°时，卫星数减少，几何分布结构变差，数学模型强度过弱，单钟差模型定位效果相对于传统方法有明显提升。Trimble NetR9在平面方向提升118.8%(1.374 m)，高程方向提升41.3%(1.434 m)；UBLOX M8T 平面方向提升9.5%(0.654 m)，高程方向提升242.9%(10.165 m)。

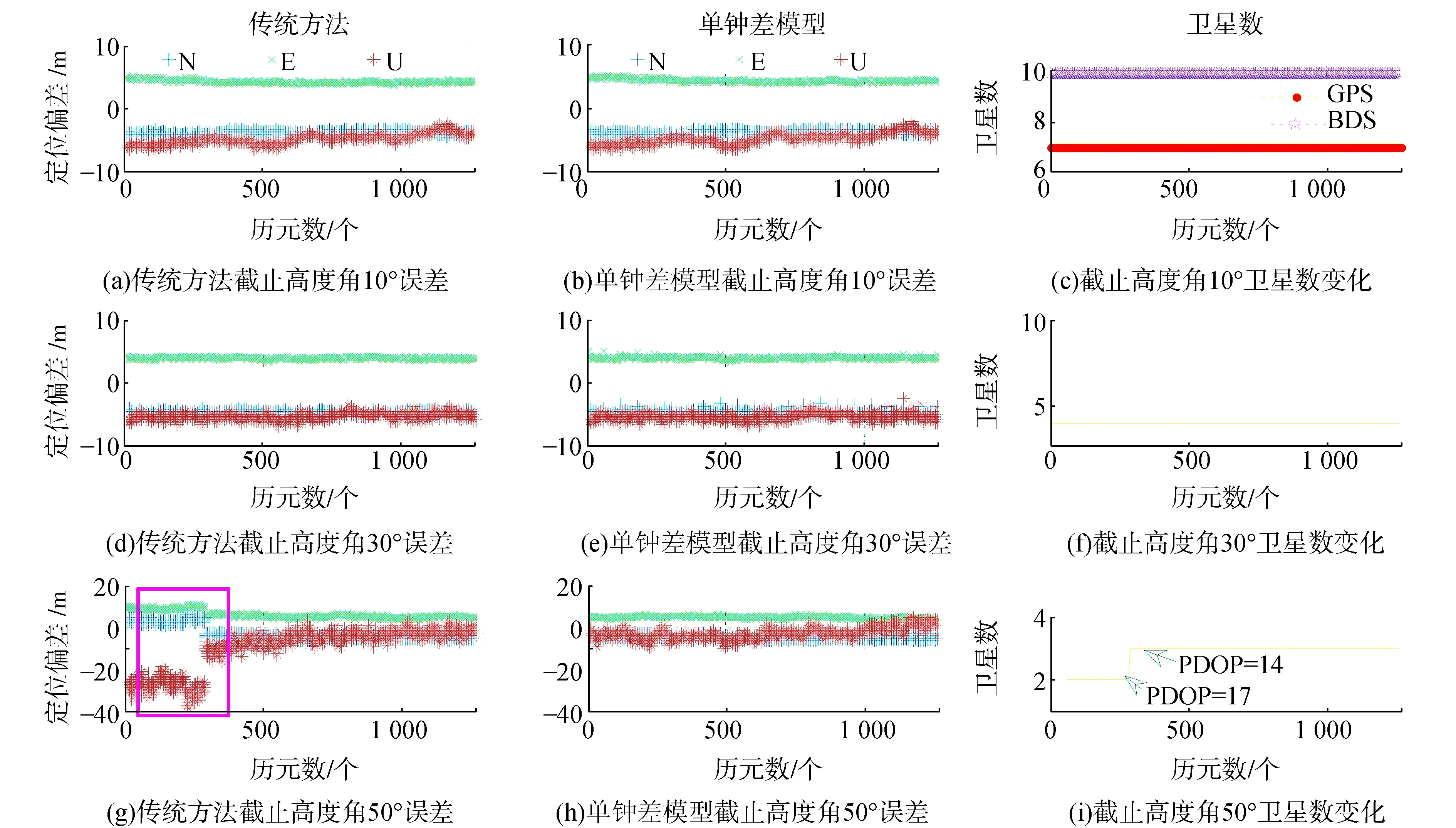
图3 UBLOX M8T定位偏差

表4 卫星过少时定位结果对比统计表

从表4可知，UBLOX M8T在卫星数过少时，相对于传统方法，单钟差模型定位效果有明显提升。其中，平面方向提升42.2%(2.707 m)，高程方向提升500.4%(23.287 m)。

综合图2、图3、表3与表4，相对于传统方法，单钟差模型在卫星数过少时能够明显提升定位效果，同时可以降低矩阵求逆维数，减少计算量。

3 结 论

本文研究一种顾及接收机ISB时域稳定特性的单钟差模型定位算法。该算法首先在卫星数足够的情况下对每个系统均引入一个接收机钟差参数，获取ISB信息，当进入遮挡环境，卫星数较少时，将前述所得ISB作为已知信息，以减少钟差参数，提高数学模型强度，从而提高定位精度与可靠性，并能够降低矩阵求逆维数，减少计算量。

为验证算法的可行性并顾及大众消费水平，共选取Trimble NetR9 与 UBLOX M8T 两种接收机数据进行验证。首先分析BDS/GPS系统间偏差的时域稳定特性，系统间偏差在100 min的稳定度分别为0.135 m和0.218 m，在数分钟内能够满足单钟差模型定位对系统间偏差稳定性的要求。接着对比传统方法与单钟差模型的定位效果，结果表明，在卫星数较少的情况下，单钟差模型能够显著增强定位效果。相较于传统方法，单钟差模型能够更好地应用于导航领域。

实际上，单钟差模型定位算法在多系统联合定位中效果提升会更明显，例如在BDS/GPS /GLONASS/GALILEO 四系统定位中，相比于传统方法可以减少3个钟差参数，多提供3个冗余观测量， 将矩阵求逆维数从7维降至4维，减少计算量，这也是本文下一步将研究的内容。