多类重力场模型的精度分析

郭春喜，张盼盼,马艳鸽

(1.长安大学 地质工程与测绘学院，陕西 西安 710064;2.国家测绘地理信息局大地测量数据处理中心，陕西 西安 710054)

高分辨率、高精度的地球重力场模型在物理大地测量中发挥着重要的作用[1-2]。随着卫星重力计划的实施，使得重力场模型的精度和分辨率得到改善，CHAMP、GRACE、GOCE等重力卫星使得全球重力场模型的中低阶的精度提高两个量级或者更高[3-4]。章传银等[5]利用大陆的GPS水准实测高程和空间异常数据，对EGM2008重力场模型进行外部检核。Gilardoni[6]等利用GOCE重力卫星数据和EGM2008构建GECO超高阶重力场模型。GKostelecky等[7]利用GNSS/水准数据对EIGEN-6C4重力场模型进行外符合精度的检核。郑增记等[8]从重力场模型的大地水准面起伏误差阶方差及位系数差阶方差两个方面对GOCE卫星重力数据建立的重力场模型进行分析，得出相较于GRACE卫星，GOCE卫星所获得的重力场信息更加精确、更加丰富的结论。赵德军等[9]从大地水准面累计误差、几何水准面与重力水准面之差和不同重力场模型之间进行谱组合3个方面评估GOCE重力场模型的精度，得出GOCE数据能够提高重力场中频、甚至高频信号的结论。但是以上文献对EGM2008、GECO和EIGEN-6C4超高阶重力场模型进行整体精度评估的研究较少，另外对于不同重力场模型之间进行组合有待进一步研究。本文首先在重力场模型的内部检核及外部检核两个方面重点探讨EGM2008、GECO、EIGEN-6C4、GOCO03S、GO_CONS_GCF_2_DIR_R5和GO_CONS_GCF_2_TIM_R5的精度趋势，并分析不同模型之间的差异。其次，对GOCO03S、GO_CONS_GCF_2_DIR_R5和GO_CONS_GCF_2_TIM_R5重力场模型选取合适的截断阶次，进一步联合EGM2008、GECO或EIGEN-6C4超高阶重力场模型进行不同阶次的组合获得组合重力场模型，可望提高重力场模型的精度。

1 原理与方法

1.1 高程异常计算

根据重力场模型,计算GNSS控制点P的模型高程异常[3,10]：

(1)

1.2 重力场模型的内符合精度检核

重力场模型的内符合精度检核通常有两种方法，一种是比较重力场模型的阶方差，另一种是比较不同重力场模型之间位系数差的阶方差，两者都可以用大地水准面高的形式表示[10-11]：

(2)

(3)

(4)

(5)

其中：n=n′。

1.3 重力场模型的外符合精度检核

利用GNSS/水准数据进行重力场模型的外符合精度检核，由式(1)可计算GNSS控制点P的模型高程异常ξp，由GNSS/水准数据确定高程异常的方法为

ζGNSS/水准=H-h.

(6)

式中：H为大地高，h为水准实测的正常高。因此可以得出残差高程异常为

Δζ=ζGNSS/水准-ζp.

(7)

则利用下式进行重力场模型的外符合精度评定

(8)

式中：n为观测值的个数。

1.4 组合重力场模型的确定

组合重力场模型是对低阶重力场模型截取可靠的阶次，对超高阶重力场模型利用低阶重力场模型进行不同阶次的组合，得到各自对应的组合重力场模型。具体的步骤：

1)对低阶重力场模型选择截断阶数k(k=10，20，30，…，N；N为低阶重力场模型的最大阶数)，组成新的重力场模型，新模型的0～K阶由低阶重力场模型获取，K到2 190阶由超高阶重力场模型相应的阶补充得到。

2)利用新的重力场模型计算GNSS点对应的模型高程异常，由式(7)计算残差高程异常，然后由式(8)计算模型的精度。

3)选择精度最高的模型为最终的组合重力场模型，其对应的阶数k为最佳的截断阶数。

2 算例分析

2.1 重力场模型内符合精度检核

本文选择EGM2008、GECO、EIGEN-6C4超高阶重力场模型及GOCO03S、DIR_R5和TIM_R5低阶重力场模型进行实验分析，由式(2)计算6个重力场模型的大地水准面阶方差，结果见图1。由图1可以看出：EGM2008、GECO、EIGEN-6C4及DIR_R5四个重力场模型的阶方差均保持在mm级，而GOCO03S模型在0～191阶的阶方差保持在mm级，191阶之后的精度达到dm级，TIM_R5模型在0～228阶的阶方差保持在mm级，228阶之后的精度达到dm级；EGM2008、GECO及EIGEN-6C4三个超高阶模型的阶方差最大分别出现在108、215和358阶，在此之后阶方差逐渐变小，而GOCO03S、DIR_R5和TIM_R5模型的阶方差最大分别出现在248、298和279阶，此时已接近其最大阶数；GOCO03S、DIR_R5和TIM_R5模型中低阶位系数与EGM2008模型相比，各模型阶方差分别在168、229和194阶之前都小于EGM2008模型的阶方差，由于3个模型中都加入GOCE卫星数据。GOCO03S在109阶之前的阶方差略小于GECO模型的阶方差，由于GOCO03S模型除利用GOCE卫星信息，还加入GRACE、CHAMP卫星信息和激光测距的信息。TIM_R5的阶方差基本都大于GECO模型的阶方差，由于GECO模型除了利用GOCE卫星数据的信息之外，还利用了GRACE卫星的信息。DIR_R5模型的阶方差在227阶之前小于GECO模型的阶方差，这是由于DIR_R5模型不仅利用了GOCE数据，还利用了25a的LAGEOS激光测卫的数据以及8a的GRACE数据。GOCO03S、DIR_R5和TIM_R5模型的阶方差大体上都大于EIGEN-6C4模型的阶方差，这是由于EIGEN-6C4模型的求解过程中加入25a的LAGECO激光测距数据、k波段变率数据、(92/12)a的SST数据以及350 d的GECO数据； DIR_R5和TIM_R5模型的阶方差在150阶之内基本保持一致，150阶之后， TIM_R5模型的阶方差明显小于TIM_R5模型的阶方差，同样这是由于DIR_R5模型不仅利用了GOCE数据，还利用了25a的LAGEOS激光测卫的数据以及8a的GRACE数据。GOCO03S模型阶方差在130阶之后明显大于DIR_R5和TIM_R5模型的阶方差，这是由于GOCO03S模型仅利用短时间的GOCE卫星观测数据；EGM2008的阶方差在235阶之前大于GECO模型的阶方差，因为GECO模型的求解过程中引入了GOCE卫星数据来改善高频信息，在235阶之后二者的阶方差相同；EIGEN-6C4模型的阶方差除在251～374阶之外，阶方差均小于EGM2008和GECO模型的阶方差，同样是由于EIGEN-6C4模型的求解过程中加入了25a的LAGECO激光测距数据、k波段变率数据、(92/12)a的SST数据以及350 d的GECO数据。

图1 6种重力场模型大地水准面高阶方差统计图

根据式(2)和图1得到的重力场模型阶方差信息，利用式(4)计算6个重力场模型的累计阶方差如图2所示。从图2可以看出：6个重力场模型中，EIGEN-6C4模型的阶方差最小； DIR_R5模型的累计阶方差小于EGM2008、GOCO03S和TIM_R5模型的累计阶方差。DIR_R5模型的累计阶方差在257阶之前小于GECO模型的累计阶方差，在此之后大于GECO模型的累计阶方差；GOCO03S和TIM_R5模型的累计阶方差小于EGM2008模型累计阶方差的阶次分别为212和251，GOCO03S和TIM_R5模型的累计阶方差都大于GECO和EIGEN-6C4模型的累计阶方差；EGM2008、GECO和EIGEN-6C4模型的累计阶方差大约分别在300、500和370阶之后趋于稳定，变化不是很明显。

图2 6种重力场模型大地水准面高累计阶方差统计图

由于EIGEN-6C4模型的内符合精度优于其他5个模型，以该模型为基准检核其他5个的模型互差阶方差，检核GOCO03S、DIR_R5和TIM_R5低阶重力场模型互差阶方差时，EIGEN-6C4模型分别取各低阶模型的最大阶数进行计算。利用式(2)和式(5)分别计算其余5个模型的互差阶方差和互差累计阶方差如图3和图4所示。

图3 模型与EIGEN-6C4模型互差阶方差

图4 模型与EIGEN-6C4模型互差累计阶方差

由图3可以看出：对于EGM2008、GECO超高阶重力场模型的互差阶方差在高频部分呈现出较大的差异，而在超高阶部分两种模型的互差阶方差表现出很好的符合性；对GOCO03S、DIR_R5和TIM_R5低阶重力场模型，150阶之后，DIR_R5模型的互差阶方差最小，TIM_R5模型的互差阶方差次之，GOCO03S模型的互差阶方差最大。

由图4可以看出：EGM2008模型的位系数差累计阶方差大约在250阶之后趋于稳定， GECO模型的位系数差累计阶方差大约在350阶之后趋于稳定；GECO模型的位系数差累计阶方差明显小于EGM2008模型的累计阶方差，由于GECO模型中加入GOCE卫星数据，其0～360阶的精度得到改善。3种低阶重力场模型的位系数差的累计阶方差中，DIR_R5模型的位系数差的累计阶方差最小。

2.2 重力场模型外符合精度检核

本文选取长江南京段控制网数据进行重力场模型的外符合精度检核，总共有53个高精度的GNSS控制点，每个点位都有基于WGS-84坐标系下的大地坐标以及二等水准高程数据。图5为点位分布图。

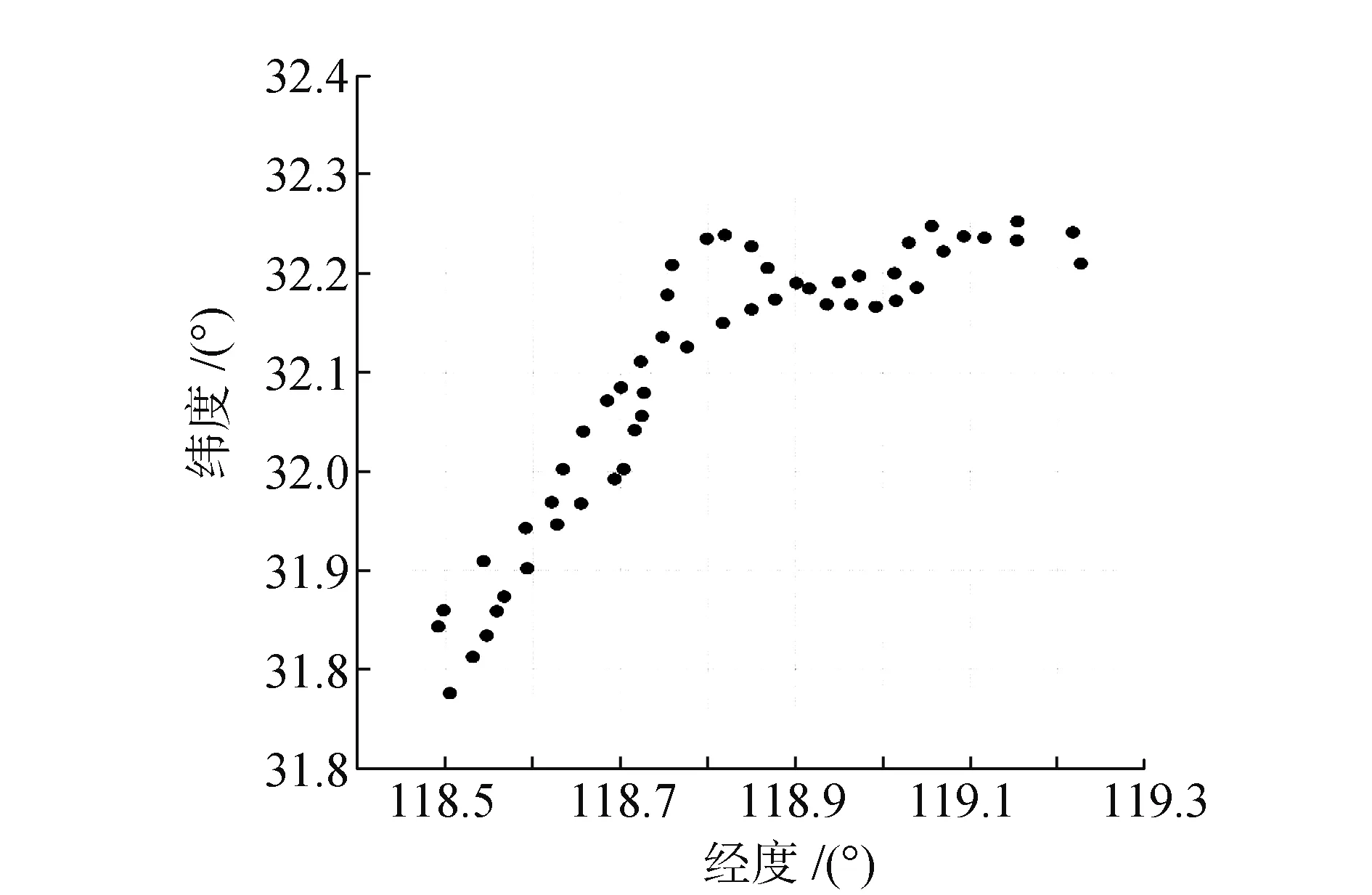
图5 点位图

对EGM2008、GECO、EIGEN-6C4、GOCO03S、DIR_R5和TIM_R5重力场模型选取不同的阶次，分别计算53个GNSS控制点对应的模型高程异常，并与GNSS/水准实测的高程异常做比较，并且利用式(8)评价精度，结果见表1。从表1可以看出：在250、280及300阶次，GOCO03S、DIR_R5和TIM_R5重力场模型的外符合精度比EGM2008、GECO和EIGEN-6C4模型的外符合精度高，说明GOCO03S、DIR_R5和TIM_R5低阶重力场模型具有精度较好的高频信息；GOCO03S、DIR_R5和TIM_R5三个低阶模型，DIR_R5模型的外符合精度最高，TIM_R5的外符合精度次之，GOCO03S的外符合精度最低；EGM2008、GECO及EIGEN-6C4模型的外符合精度明显高于GOCO03S、DIR_R5和TIM_R5模型的外符合精度以及EGM2008、GECO及EIGEN-6C4模型在250、280及300阶次的外符合精度。

2.3 重力场模型谱组合

本文对GOCO03S、DIR_R5和TIM_R5低阶重力场模型截取可靠的阶次，对EGM2008、GECO及EIGEN-6C4超高阶重力场模型利用纯卫星重力场模型进行不同阶次的组合，得到各自对应的组合重力场模型(例如：GOCO03S/ EGM2008、GOCO03S/ GECO、GOCO03S/ EIGEN-6C4等，具体表示低阶重力场模型与超高阶重力场模型的组合重力场模型)。对EGM2008、GECO及EIGEN-6C4超高阶重力场模型对应的组合重力场模型进行精度分析，结果分别见图6、图7及图8。

表1 重力场模型与GNSS/水准的高程异常比较结果 m

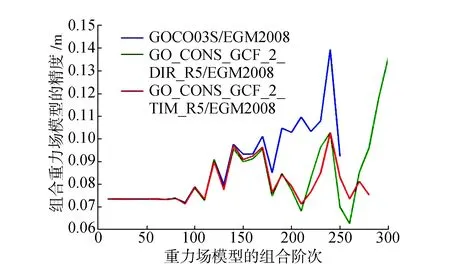
图6 EGM2008对应的组合重力场模型精度趋势

图7 GECO对应的组合重力场模型精度趋势

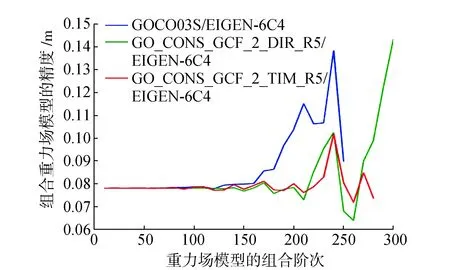
图8 EIGEN-6C4对应的组合重力场模型精度趋势

由图6、图7及图7可以看出EGM2008、GECO及EIGEN-6C4模型对应的组合模型在150阶前的精度趋势基本一致，在150阶以后各组合模型的精度趋势表现出明显差异。选择精度最高时对应的阶次为组合模型的可靠截取阶次，由图6可以看出组合模型GOCO03S/EGM2008、DIR_R5/EGM2008及TIM_R5/EGM2008的可靠截取阶阶次分别为90、260及220。由图7可以看出组合模型GOCO03S/ GECO、DIR_R5/GECO及TIM_R5/GECO的可靠截取阶次分别为90、260及230。由图8可以看出组合重力场模型GOCO03S/EIGEN-6C4、DIR_R5/ EIGEN-6C4及TIM_R5/EIGEN-6C4的可靠截取阶次分别为90、2600及260。

组合模型以及EGM2008、GECO及EIGEN-6C4超高阶模型计算实测GNSS点位的高程异常值，并与GNSS/水准实测的高程异常值比较，结果见表2。由表2可以看出，在本实验区域：EGM2008模型对应的组合模型精度最优为0.063 m，最差为0.072 m，而EGM2008模型的精度为0.074 m，因此高程异常的精度提升15%；组合模型的精度比EGM2008的精度高；GECO模型对应的组合模型精度最优为0.060 m，最差为0.074 m；而GECO的精度为0.078 m，因此高程异常的精度最高提升23%；组合模型的精度比GECO的精度都要高；EIGEN-6C4模型对应的组合重力场模型精度最优为0.064 m，最差为0.077 m；而EIGEN-6C4的精度为0.078 m。因此高程异常的精度最高提升18%；组合模型的精度比EIGEN-6C4的精度都要高；3种低阶重力场模型对超高阶模型的精度提升能力从大到小依次为DIR_R5、TIM_R5及GOCO03S。

表2 超高阶模型及其对应的组合重力场模型与实测高程异常比较结果 m

3 结 语

1)EGM2008、GECO、EIGEN-6C4及DIR_R5四个模型的阶方差均保持在mm级，而GOCO03S模型在191阶之后的精度达到dm级，TIM_R5模型在228阶之后的精度达到dm级。6个重力场模型中，EIGEN-6C4模型的累计阶方差最小。

2)GOCO03S、DIR_R5和TIM_R5模型中低阶位系数与EGM2008模型相比，各模型阶方差分别为168、229和194阶之前都小于EGM2008模型的阶方差，说明采用GOCE卫星数据可以提高重力场模型的高频精度。

3)EGM2008、GECO模型的互差阶方差在高频部分呈现出较大的差异，而在超高阶部分两种模型的互差阶方差符合性好；EGM2008模型的位系数差的累计阶方差大约在250阶之后趋于稳定， GECO模型的位系数差的累计阶方差大约在350阶之后趋于稳定；3个低阶重力场模型的位系数差的累计阶方差中，DIR_R5模型的位系数差的累计阶方差最小。

4)利用GNSS/水准数据检核组合重力场模型表明，组合重力场模型能提高重力场模型精度。EGM2008对应的组合重力场模型精度比EGM2008精度至少提高3%，最优提高15%。GECO对应的组合重力场模型精度比GECO精度至少提高5%，最优提高23%。EIGEN-6C4对应的组合重力场模型精度比EIGEN-6C4精度至少提高2%，最优提高18%。

5)3个低阶重力场模型对超高阶模型的精度提升能力从大到小依次为DIR_R5、TIM_R5及GOCO03S。