问题解决教学存在的问题及对策研究

江苏南京市百家湖小学 焦欢欢

一、实践中存在的问题

小学数学中问题解决教学一直是一线教师关注的重点，不少教师花费很大力气，依然收效甚微，问题出在何处？笔者通过实践观察，发现问题解决教学主要存在以下几点问题：

（一）忽视学生认知结构的建构

教师过于追求学生解决问题的“量”，却忽略对问题进行精心有效的编排，碎片化的题目使学生没有形成清晰的问题结构，在遇到此类问题时，认知无法快速提取相应的问题类型。因此，教师要从“零散点状研究”转向重视整体性的“认知结构”的建构。

（二）忽视学生方法的外显表达

教师过于重视对学生的“方法输入”，忽视学生的“方法输出”，忽略学生对方法的建构与外显表达，造成学生关键时刻无法提取相应的方法。只有经过学生建构的方法，才更容易被学生内化，才能在恰当时刻被认知提取出来，解决当前的问题。

（三）忽视学生反思意识的培养

教师过于关注解决问题的结果，学生长期处于向前“赶”的状态，却没有时间“回头”反思学习过程，缺乏反思意识。反思，让学生的学习过程通透起来、串联起来，让学生的思维清晰化、深刻化、全面化，让学生站在更高的角度去调整和规划自己的学习。

二、问题解决教学策略研究

基于以上存在的问题，笔者在问题解决教学实践中展开如下策略。

（一）精心设计题组，让学生的问题认知趋于结构化

题组，是指遵循学生的认知规律，按照一定的关系，将一组数学问题编排组合。这种题组并不是几个独立数学问题的简单组合，而是通过内在联系进行有效编排，让学生形成对问题本质结构的理解，进而让学生对问题的认知趋于结构化。

1．设计同类型题组，构建学生的问题结构

同类型题组是指把本质相同的问题设计成题组的形式，学生根据同类题组关系，看清问题的内部结构，大脑中能迅速调动相应的思维方法。在教学归一问题时，笔者出示如下同类型题组：

（1）买3枝百合花用了18元，买8枝同样的花，需要多少钱？

（2）3枝百合花用了18元，30元可以买几枝？

（3）3天读了24页，照这样速度，7天可以读多少页？

（4）2张照片发送了6秒，照这样的速度，发送7张照片，需要多长时间？

（5）3个同学擦了12块玻璃，教室有36块玻璃，一共需要几个同学？

师：回顾我们解决的这么多问题，你觉得解决这些问题有什么共同的地方？

生：都是先求一种东西的多少。

师：刚才你们说的“一”，其实在数学里，我们把它叫作一份数，今天我们解决的这类问题，我们就把它叫作“归一问题”，遇到这样的问题，你们怎么办呢？

生：我们要根据条件，算出一份的数量，再算出几份的数量。

教师出示不同情境但问题结构相似的同类型题组问题，将学生的注意力聚焦在问题的本身，从整体上感知问题的结构。教师通过启发学生“这些问题有什么相同的地方”，在比较后，从中抽象出共性：都要先算一份，再算几份。教师帮助学生建立更上位的知识框架与体系，构建学生“归一问题”的问题结构。

2．设计对比型题组，活化学生的问题结构

对比型题组是指在情境、内容上看似相同，但数学本质却存在不同，通过对比型题组，学生学会灵活判断问题情境和结构，而不再拘泥于机械文字，活化了学生的问题结构，让学生的问题结构更灵活。例如，笔者在学生初步建立问题结构的基础上，设计以下一组对比题型：

（1）一块布长20米，3米可以做一套衣服，这块布最多可以做几套衣服？

（2）有20个人去划船，每条小船最多坐3人，至少需要多少条小船？

上面两题，第一步都用到算式20÷3=6……2，但最终的结果却不同。笔者抓住题目不同之处进行追问：为什么第一题答案是6，第二题答案是7呢？学生在这样的对比中，弄清了题目的差异。第一题是问20米里面最多有几个3米，而第二问，因为人全部要坐上船，最后的两人也要坐上船。通过这样的对比，学生克服了解决问题的机械性，而是根据具体问题情况，灵活运用，培养学生认知结构的灵活性。

3．设计递进型题组，深化学生的问题结构

递进型题组是指由浅入深设计的一组难度逐步递增的题目组合。在逐步解决递进题组的过程中，学生的思维经历由浅入深，逐步培养学生思维的深刻性。特级教师张勇林在执教“解决分数问题的复习课”时，通过设计递进型题组，逐步深化学生的问题结构。教师出示“数学与生活”小论文获奖情况如右图：

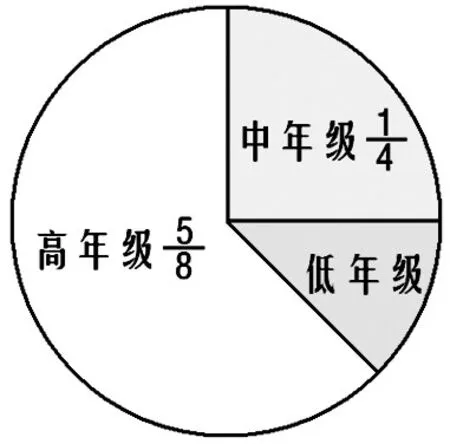
师出示问题1：全校获奖篇数480篇，那高年级有多少篇获奖？

师出示问题2：如果中年级有120篇获奖，那高年级有多少篇获奖？

师出示问题3：如果中年级有120篇获奖，那低年级获奖多少篇？

纵观以上三题，第一题学生只需找单位“1”，用乘法计算；第二题则需要两步：先用除法计算找出单位“1”，再用乘法计算；第三题需要经历三步：先找对应分率，再用除法计算找出单位“1”，最后求单位“1”的几分之几，用乘法计算。这三道问题逐层变化，教师通过设计递进型题组，由单位“1”已知变化到单位“1”未知，再变化到找出对应分率和单位“1”，学生需要的思维运算操作逐步增加，每层思维运算都要借助上一层，层层递进，使分数问题内容螺旋式上升，从低级到高级，深化了学生的问题结构。

（二）鼓励学生用图示表达，让学生的思维过程外显化

图示，是指用图形或结构来说明某种东西，往往比较直观，浅显易懂。在面对数学问题时，教师要鼓励学生用图示表达，用自己的表达方式去表征知识、建构知识，通过直观的图示，让学生内隐的思维过程得以外显化。在教学中，学生常常会进行以下三种图示表达：

1．文字摘录——条件选择外显化

例如，在一次作业中，有这样一题：学习食堂买来5筐番茄、3筐大白菜和2筐萝卜。每筐番茄28千克，每筐大白菜35千克，每筐萝卜32千克。番茄和萝卜一共多少千克？大白菜和萝卜一共多少千克？笔者让学生自主表达，学生整理如下：

面对复杂的条件，学生稍不注意便会出错，而当学生从问题选择有用的条件时，思路便清晰可见。当出示番茄和萝卜一共多少千克时，学生自主梳理番茄和萝卜的相应条件，在摘录条件的过程中，学生选择条件的思维过程得以外显化。

2．线段图——数量关系外显化

在解决问题教学时，有的问题经常分歧很大，这时，教师不妨让学生以“自己的”方式建构与表达，以培养学生分析数学问题的能力。如笔者在课堂教学中，遇到这样一题：玲玲看一本故事书，平均每天看35页，看了5天后正好看了剩下页数的一半，这本书一共有多少页？

生：先用35×5=175（页），因为看了一半，所以再用175×2=350（页）。

师：同意的同学举手看看(统计发现居然全班一半人同意）。

师：你能把你的想法画出来吗？（学生画图如下）

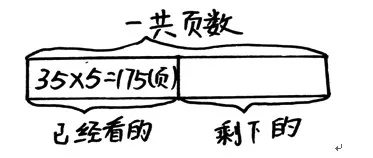
生1：老师，他画的不对，已经看的175页是剩下页数的一半，不是等于剩下页数。

生2：已经看的是剩下页数的一半，也就是剩下页数相当于两个已经看的部分。

（画图的学生恍然大悟，重新调整示意图）

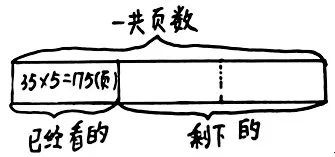
师：从现在这个图中，你们看出了什么？

生：已经看的页数是剩下页数的一半。

生：整本书页数相当于已经看的页数的3倍。

在“画”的过程中，学生错误的思维暴露出来，数量关系得以外化，正是这样的图示表达，促进了学生对数量关系的理解，分歧的问题迎刃而解。

3．流程路——解题思路外显化

在一次作业中，有这样一题：某停车场收费规定，大客车第一个小时收费3元，以后每小时收费4元；小轿车前2小时收费4元，以后每小时收费3元。一辆大客车停车5小时需要缴费多少元？笔者想了解学生是如何理解这个问题，便让学生以自己的方式来解决，在作业中有学生画出如下流程图：

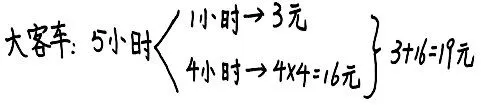
课堂中，笔者紧接着出示这样一问：一辆小轿车离开停车场时，付了19元，该小轿车停车几个小时？其他学生自主迁移这位同学流程图的画法，将问题整体攻破，形成如下流程图：

在画流程图的过程中，学生认知不仅需要整体地分析条件，还要整体思考问题的结构与顺序，在画的过程中，复杂问题变得简单化、清晰化、结构化。

（三）引导学生反思，在反思中培养元认知能力

元认知是指对认知的认知。具体说是关于个人自己认知过程的知识和调节这些过程的能力，对思维和学习过程的认识和控制。它对于提高学生问题解决能力至关重要，能起到调节、发动的作用。笔者在教学中，经常引导学生在以下几处反思：

1．在错误处反思，看清思维障碍处

在一次课堂教学中，遇到这样一题：树上先飞走7只鸟，又飞走5只鸟，两次飞走多少只鸟？用减法和加法的人各一半。

生1：这里是飞走，飞走用减法算。

生2：我不同意，这里虽然是飞走，但是是求两次飞走，是求一共，要把两次飞走的合起来。

生3：我也不同意减法。如果用减法算7-5=2，两次怎么一共才飞走2只呢，第一次就已经飞走7只了。

生2：对呀，而且这道题目又没有告诉你一开始一共有多少只，不是从一共的里面去掉。（这时，不少学生改变了自己原先错误的想法）

师：犯错没关系，反思刚才错误的地方，你有什么想和大家分享的？

生1：看到飞走，就感觉像减法，但现在看来飞走不一定就是用减法算。

生2：掉进文字的陷阱里了。

生3：看来到底用加法还是减法，不能光靠感觉，要明白是求合起来还是求从一共里去掉一部分，求另一部分。

笔者在这个环节，并没有止于纠正错误，而是让学生反思错误，在反思中看清思维障碍处，突破加减法的意义，让学生不停留于表面，而是深入理解加减法的含义。

2．在困惑处反思，突破思维模糊点

学生在面对问题时，常常会出现“似会不会”的状态，即对问题还存在困惑之处。遇到这样的问题，教师要让学生学会慢下来，认真反思困惑之处，改变“似会不会”的状态，突破思维模糊点。在一次练习中有这样一题：一个时钟6时整敲6下，10秒敲完，如果这个钟敲12下，需要多少秒？班上一半的学生在20秒和22秒之间犹豫不决，究其原因，是学生没有彻底明白这个问题的本质。笔者课堂追问：敲钟这个动作很快，这么快的动作，为什么敲6下需要10秒呢？学生通过反思明白：每敲两下之间会有时间间隔，敲6下是间隔5段，5段时间是10秒，一段时间是2秒，由此很快推出，敲12下是11段，时间是22秒。当学生反思自己困惑处，找到关键，便突破思维模糊点，对于类似间隔问题能举一反三。

3．顿悟处反思，寻找思维突破口

在问题解决的过程中，学生常常在苦思冥想后突然顿悟，这时，教师要引导学生在顿悟处反思，是因为想到什么从不会到会？以后遇到问题如何去寻找突破口？一旦学生形成这样的反思意识，将提高学生寻找问题突破口的能力。笔者的学生曾经遇到这样一个问题：用一个杯子向空水壶里倒水，如果倒进3杯水，连壶重660克，如果倒进5杯水，连壶重900克。每杯水重多少克？空水壶重多少克？笔者观察班上一位学生，在凑数、画图分析之后，由愁眉不展到喜悦地感叹：原来是这样！笔者与该生展开以下对话：

师：你怎么解决这个问题的？

生：老师，我突然发现，为什么第二次水连壶更重了，从之前660克到现在的900克，那是因为多加了2杯水，2杯水就是900-660=240克。

师：之前怎么没想到呢？

生：之前我只盯着每句话单独看。

师：看来，解决问题一定要用联系的眼光看，说不准会找到问题的关键点和突破口。

生：是的，这个问题最关键的是前后重量的变化，多的重量就是2杯水的重量！

师：是的，要在变与不变中寻找到关键的突破口。