基于相对熵方法的长寿债券定价研究

宋平凡，谭常春，祁 毓

(1.合肥工业大学经济学院,安徽 合肥 230601;2.中南财经政法大学财税学院，湖北 武汉 430073)

1 引言

随着生活水平的改善和医疗技术的进步，我国居民的人均寿命正在大幅提高。根据世界银行的数据显示，我国居民的人均出生预期寿命由1990年的69.3岁上升到了2016年的76.2岁。人均寿命大幅改善是社会进步的重要体现，但也给居民养老问题带来了一定挑战。尤其是计划生育国策使我国的人口生育率降低，更加剧了人口老龄化问题。根据国家统计局发布的《2017年国民经济和社会发展统计公报》显示，截至2017年末，我国60周岁以上的老龄人口占比为17.3%；65周岁以上的老龄人口占比为11.4%。如何应对人口老龄化，如何解决养老问题，正成为当前社会不得不正视的严峻现实。由于人口老龄化和居民寿命改善将使得养老金支出大幅增加，我国养老保障的“三支柱体系”均将面临着随之而来的财务冲击。这种由于居民整体寿命改善而给养老基金或保险公司带来的财务风险被称为长寿风险。要想妥善处理居民养老所承受的资金压力，就必须积极主动地寻找科学管理长寿风险的方法，这也与十九大报告提出的“实施健康中国战略，积极应对人口老龄化”的观点相契合。

然而长寿风险管理并非易事，由于保险经营基本原理是运用大数定律分散风险，但保险公司和养老金机构面临的长寿风险是不可分散的系统性风险，因而长寿风险管理需借助其他渠道。目前被学界关注到的长寿风险管理方法主要有两种，一种被称为自然对冲[1-3]，该方法是利用寿险业务和年金业务现金流变化完全相反的特性，当人均寿命增加时，通过寿险业务的增值去对冲年金业务的长寿风险。另一种引起学者关注的方案则是通过在资本市场发行金融衍生品(后文对该类衍生品简称为长寿衍生品)来对长寿风险进行对冲。在实践中长寿衍生品也有过先例，比较典型的是欧洲投资银行(European Investment Bank)和法国巴黎银行(BNP Paribas)联合发行的长寿债券(后文简称EIB/BNP型长寿债券)。该债券的发行虽然最终并未获得成功，但作为典型长寿债券实例，仍吸引了学者以之为对象展开研究。一些学者把EIB/BNP作为长寿衍生品的典型案例进行了分析[4-5]，但系统全面地介绍各类长寿衍生品以及长寿债券发行原理和特点的文献至少可以追溯到Blake等[6-7]的研究。与一般金融衍生品的发行相似，长寿衍生品发行的核心问题是定价。在该问题的研究过程中，学者们进行了大量尝试和探索，但各种定价方法也不可避免存在局限性。如Friedberg 和Webb[8]运用资本资产定价模型(CAPM)和基于消费的资本资产定价模型(CCAPM)来对长寿衍生品进行定价，但他们本人也承认实际的风险市场价值要比使用该模型计算得到的结果高出许多；一些文献提出了Sharpe比率法[9-10]，但该方法又被认为本质上趋同于市场风险价格为常数情形下的风险中性测度定价方法[11]； Wang[12-13]提出的“Wang转换”方法虽然在长寿衍生品定价领域得到一定应用，但也被质疑“并不能提供统一的理论框架”[14-15]。对于各种定价方法的原理和局限，已有部分文献进行了总结和比较[16-17]。一些研究也将经典的风险中性测度理论引入到长寿衍生品定价领域[18-21]，但在非完全市场中，风险中性测度Q并不唯一。为了解决这个问题，Li[22]使用了Kullback-Leibler相对熵方法(Kullback-Leibler relative entropy, 后文简称KL相对熵, 有些场合也将相对熵称作交叉熵，即cross entropy)。相对熵方法的引入从理论上解决了Q测度的选择问题。这种方法在后续有关定价问题的研究中，也有了更多地应用[21,23]。因此总体来看，在风险中性测度框架下使用相对熵方法是优越性相对较高的一种选择。

对长寿风险衍生品定价而言，除了定价方法和定价理论的选择，人群的死亡率进行建模和预测也比较重要。早期的死亡率模型以静态的模型为主，例如Gompertz模型[24]，Heligman和Pollard[25]提出的HP模型，还有Carriere[26]提出的CR模型等,该类模型的缺点是只考虑年龄因素而不考虑时间因素，适用于配合生命表进行不同年龄死亡率的推算，但无法反映死亡率随着不同年份的变化趋势。Lee和Carter[27]提出了既考虑年龄因素也考虑时间因素的动态死亡率预测模型，即Lee-Carter模型，在此之后，死亡率建模时主要采用的都是动态化的模型，如Cairns等[28]提出的Cairns-Blake-Dowd两因子模型(简称CBD两因子模型)。Lee-Carter模型主要用于不同年份的不同年龄群组整体死亡率的建模(如10-14岁群组)，CBD模型则可用于模拟不同年份具体年龄的人群死亡率，且对高龄人口的预测效果要更好一些。近期的相关死亡率建模开始关注到不同人群死亡率的相依性，例如Yang和Wang[29]使用向量误差修正模型研究了不同国家人群死亡率的长期均衡关系，还有一些研究使用了Copula方法去刻画了不同人群死亡率相依性的研究[30-31]，但该类研究依赖于较长期的历史死亡率数据建模，目前还不具备使用我国数据进行类似建模的条件。

总之，无论是定价方法还是死亡率预测模型的发展，都推动了长寿衍生品的研究，尤其是关于长寿债券的研究。作为关注度较高的长寿衍生品，长寿债券有可能成为实践中有力的长寿风险管理工具。目前国内的学者也开始重视我国的长寿债券定价问题[32-37]。与EIB/BNP这种连续型的长寿债券不同，国内的研究大多构造了类似期权原理的触发式长寿债券，这种债券的作用原理与Swiss Re在2003年底发行的死亡率巨灾债券原理相似， 但这种死亡率巨灾债券的初衷并非用来对冲长寿风险，相反地，其用途主要是对冲极端灾害事件(如地震、海啸和大范围疾病)带来寿险业务的偿付风险，但通过制定不同的标的指数和触发阈值，亦可构造出形式相似但用于管理长寿风险的债券。本文期望推动长寿衍生品定价研究的发展，并为我国长寿风险的有效管理做出贡献。本文所做的工作主要有：首先以历年分年龄的死亡率数据为基础，使用更适合高龄人口死亡率建模的CBD两因子模型对未来不同性别人群的死亡率进行模拟和预测；同时采用相对熵方法，并融合我国金融市场上所拥有的市场风险价值信息，对EIB/BNP型长寿债券进行定价。和之前的研究相比，本文可能的创新点有如下几条：在研究内容上，本文以风险中性测度理论为框架，基于我国死亡率数据对EIB/BNP型长寿债券进行定价，同时，定价过程中也考虑了我国金融市场的风险价值信息，使长寿债券定价的结果与我国人口死亡率情况和金融市场状况更契合；在研究方法上，本文拓展了相对熵方法在长寿衍生品定价领域的应用，在求解最优风险中性测度时不仅使用了KL相对熵，还使用了Tsallis相对熵以及Rényi相对熵方法，保证了计算结果的稳健性；在对实证工作的总结上，与以往文献不同，本文并非仅仅列出定价结果，而是更注重从实证结果中挖掘出我国长寿风险所面临的实际特点，以及在长寿风险管理工作中需要注意的问题，可为长寿风险管理提供有价值的参考建议。

2 EIB/BNP长寿债券简介

限于篇幅，本文仅对EIB/BNP的债券定价发行和偿付机制进行简单介绍，该债券详细的发行流程可见参考文献[5]。欧洲投资银行(EIB)和法国巴黎银行(BNP)于2004年联合发行了面值为5.4亿英镑，期限为25年的长寿债券，该债券主要面向养老基金以及年金机构，具有浮动的息票支付，每年向投资者的息票支付为50,000,000×I(t) (单位：英镑)，其中I(t)表示第t年的生存指数，该指数与特定人群的历年死亡率挂钩：

(1)

其中mx,t表示在第t年x岁的人群的死亡概率，t=0表示初始计息的前一年份。若在我国发行该类型债券，为方便讨论，假定1×I(t)(单位：元)为息票支付，则该债券在0时刻的定价为

(2)

其中δ表示长寿风险的溢价，代表长寿风险的“市场价格”。需要指出的是，本文对长寿债券进行定价，实质上就是计算不同期限长寿债券对应的风险溢价δ。Ft代表到时刻t为止的信息集，B(0,t)代表t时刻偿付1元的零息债券以无风险利率(本文设定无风险利率为4%)贴现到0时刻的价格,表示在真实概率测度P下的数学期望。由于长寿债券与特定人群的死亡率挂钩，因此我们首先要获得目标人群未来死亡率的信息，本文以2017年64岁的男性和女性人群为目标人群，为了构造债券定价所需的生存指数，需要对目标人群的死亡率进行预测。

3 CBD两因子模型

由于相比Lee-Carter模型而言，CBD两因子模型对高龄人口的预测效果更好，而EIB/BNP型长寿债券正是以高龄人群死亡率构造生存指数的，因此本文采用了CBD两因子模型建模，并对目标人群的未来死亡率进行模拟。

CBD两因子模型的基本设定如下：在第t年时年龄为x的群体死亡率mt,x有如下性质：

(3)

其中，二维列向量A(t)=(A1(t),A2(t))T服从二维的随机游走过程

A(t+1)=A(t)+μ+C·Z(t+1)

(4)

其中，μ和C分别是漂移参数和扩散参数，μ=(μ1,μ2)T为一个二维的列向量，C为2×2的下三角矩阵，Z(t)=(Z1(t),Z2(t))T是一个两维的标准正态分布随机变量,V-1和μ分别服从Wishart分布和多元正态分布：

(5)

在这里，V=CCT,即C是V的Cholesky分解,同时还有

D(t)～A(t)-A(t-1)

(6)

通过(4)-(6)式得到模型相关参数信息并模拟生成未来的死亡率因子A(t)，再通过(3)式进行转换即可得到目标人群未来死亡率路径。

4 最小相对熵方法

相对熵是衡量从一个测度转换到另一个测度所获得的信息增量。从贝叶斯统计学的角度来看，如果新加入的信息使原来的概率发生变化，那么新的概率测度的选择应当尽可能产生最小信息增量，这也被称作最小差别信息准则(Minimum Discrimination Information)[38]。因而通过最小化相对熵我们能够选择与真实概率测度P信息量差距最小的风险中性测度Q。相对熵也有不同种类，如经典的KL相对熵[39]，此外还有Tsallis相对熵[40]以及Rényi相对熵[41]。Li[22]使用KL相对熵研究长寿债券的定价问题，而 Tsallis相对熵和Rényi相对熵也被用于金融定价领域，例如柳向东和王星蕊[42]以及Dolan等[43]的研究。实际上， Tsallis相对熵和Rényi相对熵包含了更多的参数，使得模型具有一定的灵活性，同时Tsallis相对熵和Rényi相对熵是KL相对熵的推广，因而我们将其用于对KL相对熵方法计算得到的结果进行稳健性检验。接下来我们分别介绍如何使用三种相对熵来确定最优的风险中性测度。

模型1：最小KL相对熵方法

KL相对熵的定义为

(7)

其度量了风险中性测度Q关于真实测度P的差异程度，EP(·)表示在测度P下的期望算子。假设市场中有m种资产，存在N个概率路径。当概率路径数等于市场中的资产数量，即N=m时，市场即被称为完全市场， 此时存在唯一的风险中性测度；当概率路径数大于市场中的资产数量，即N>m时，市场即被称为非完全市场，此时风险中性测度不唯一。通过最小化KL相对熵方法来求最优风险中性测度即解决如下优化问题：

(8)

Vi表示资产i的市场价格，fi(wj)表示在第j个概率路径下第i种资产的价值。

设定拉格朗日函数形式为：

(9)

则一阶条件为：

(10)

模型2：最小Tsallis相对熵方法

Tsallis相对熵的定义为

(11)

使用最小化Tsallis相对熵方法来求最优风险中性测度即解决如下优化问题

(12)

约束条件和模型1相同。拉格朗日函数为

(13)

一阶条件为

(14)

模型3：最小Rényi 相对熵方法

Rényi 相对熵的定义为

(15)

使用最小Rényi相对熵方法求最优风险中性测度即解决如下优化问题

(16)

在约束条件不变的情况下，拉格朗日函数变为

(17)

问题求解一阶条件为

(18)

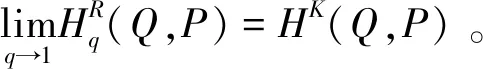
通过Matlab软件进行编程，使用数值解法在模型1-3中分别求得了最优的风险中性测度Q后，依据公式

(19)

可以计算不同期限T下长寿债券的风险市场价格，即可完成不同期限长寿债券的市场定价。

5 实证模拟

(1)死亡率建模结果

本文采用了1986年-2016年的男女不同性别人口分年龄死亡率数据，1986年—2005年的死亡率数据来源为《中国人口统计年鉴》，2006-2016年的死亡率数据来源为《中国人口和就业统计年鉴》，其中1991-1993年对应的年鉴中并未统计分年龄死亡率统计数据，故按年份采取平均插值法补齐这三年数据。由于早期死亡率数据统计仅统计到84岁，故我们选择60-84岁的人群死亡率数据作为来估计CBD两因子模型的参数，这一方面是由于长寿债券主要针对高龄人群管理长寿风险，选择高龄人口建模得到的结果更准确，对未来死亡率的模拟也更可信,另一方面Cairns等[28]还指出CBD模型对高龄人口死亡率的拟合效果更好，在该论文中他们也选择60岁以上人群的死亡率数据来估计模型的参数。

图1 1986年-2016年死亡率因子A1(t)的趋势

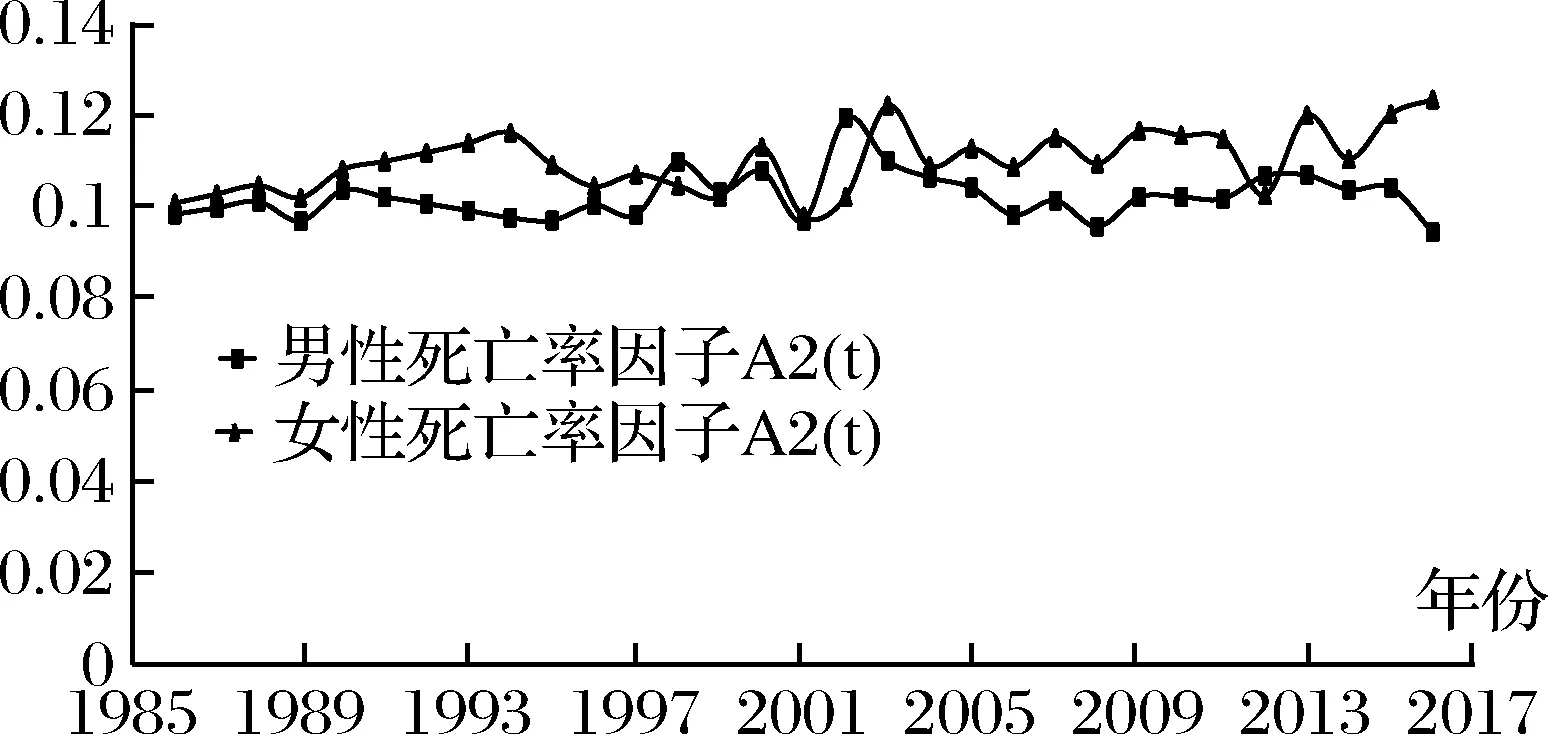
图2 1986年-2016年死亡率因子A2(t)的趋势

我们根据第3部分所列公式计算不同性别高龄人群的死亡率因子A1(t)和A2(t)以及CBD模型的相关参数。我们分别将A1(t)和A2(t)展示在图1和图2中。从图中可以看出，对于男性人口的死亡率因子，无论因子A1(t)还是A2(t)均呈现缓慢下降趋势，对于女性人口的死亡率因子，虽然A1(t)呈现更明显的下降趋势，但A2(t)反而呈现略微上升的趋势。男性死亡率模型的相关参数估计结果为：

而女性死亡率模型的相关参数估计结果为

(2)风险价格信息

风险中性测度方法依赖于现有市场的完全性，现有市场的交易资产越多，能够提供的关于风险的市场价格的信息越丰富，长寿债券的定价也会越合理。为此我们需要搜集我国市场上相关金融资产的信息。从发行主体来看，长寿债券和金融债类型最为接近。金融债是金融机构所发行的债券，资信水平往往较高，该类债券的收益率相比无风险利率略高。我们从Resset金融数据库中搜集了1998年-2018年发行的1650只金融债的期限和利率的数据，同时Resset数据库还提供了1998-2018年的参考无风险利率。Resset数据库的参考无风险利率数据在2002年8月6日之前是三个月银行定存利率；2002年8月7日-2006年10月7日是三个月期央行票据利率，2006年10月8日之后的无风险利率是上海银行间3个月同业拆借利率，此处使用参考无风险利率仅用于推算金融债的风险溢价，而在进行长寿债券定价所涉及到的无风险利率均如前文设定按常数4%计。根据债券的收益率以及无风险利率信息分别推算出了不同期限下的平均风险溢价，同时删去少数异常的样本(如债券期限非整数年以及风险溢价为负数等)；由于EIB/BNP债券的期限是25年，我们也剔除了期限超过25年的超长期限债券，防止期限过长影响计算结果的准确性。我们将最终获得的6种不同期限金融债的平均风险溢价信息展示在表1中，并将这6种“期限-溢价”的组合分别以A-F表示。A-F这几种“期限-溢价”组合即代表了当前市场所能提供的6种风险的市场价格信息。

(3)只考虑单个风险价格

假设仅包含单个风险市场价格信息，即仅有一种资产(m=1)，且以组合E的形式出现,根据该组合的期限(10年)和风险溢价(δ=0.0069)代入到式(2)中计算出该资产的价格，并代入模型1- 3的约束条件中，即可分别计算出最优风险中性测度Q，然后根据式(19)计算反推出不同期限的长寿债券的溢价信息。我们将结果展示在图3-图5。

表1 金融市场不同“期限-溢价”组合

图3 KL相对熵计算的风险溢价(m=1)

首先可以看出，在仅由一种资产提供市场信息时，男女人群长寿风险溢价的整体趋势差异不大，当债券期限逐渐大于资产E的期限时，男女人群长寿风险的市场价格基本趋同。这种趋势在使用三种相对熵方法时表现一致；此外在使用Tsallis相对熵和Rényi相对熵时，我们还分别设置了不同模型参数α和q，但对最终结果影响很小。这表明了仅包含单个资产信息时，使用相对熵方法以及对不同性别人群的长寿风险进行定价，较难得到的有差异的风险市场价格信息。

图4 Tsallis相对熵得到的风险溢价 (m=1)

图5 Rényi相对熵得到的风险溢价 (m=1)

(4)考虑多个风险价格

接下来假设市场包含多个风险市场价格的信息，不妨假设要运用A-F这6种“期限-溢价”组合来为债券正确定价提供信息，即在模型1-3中，m=6。分别根据式(2)求出这6种资产的价值，并代入模型1-3的约束条件来求解模型，然后将所得到的结果呈现在图6-图8中。

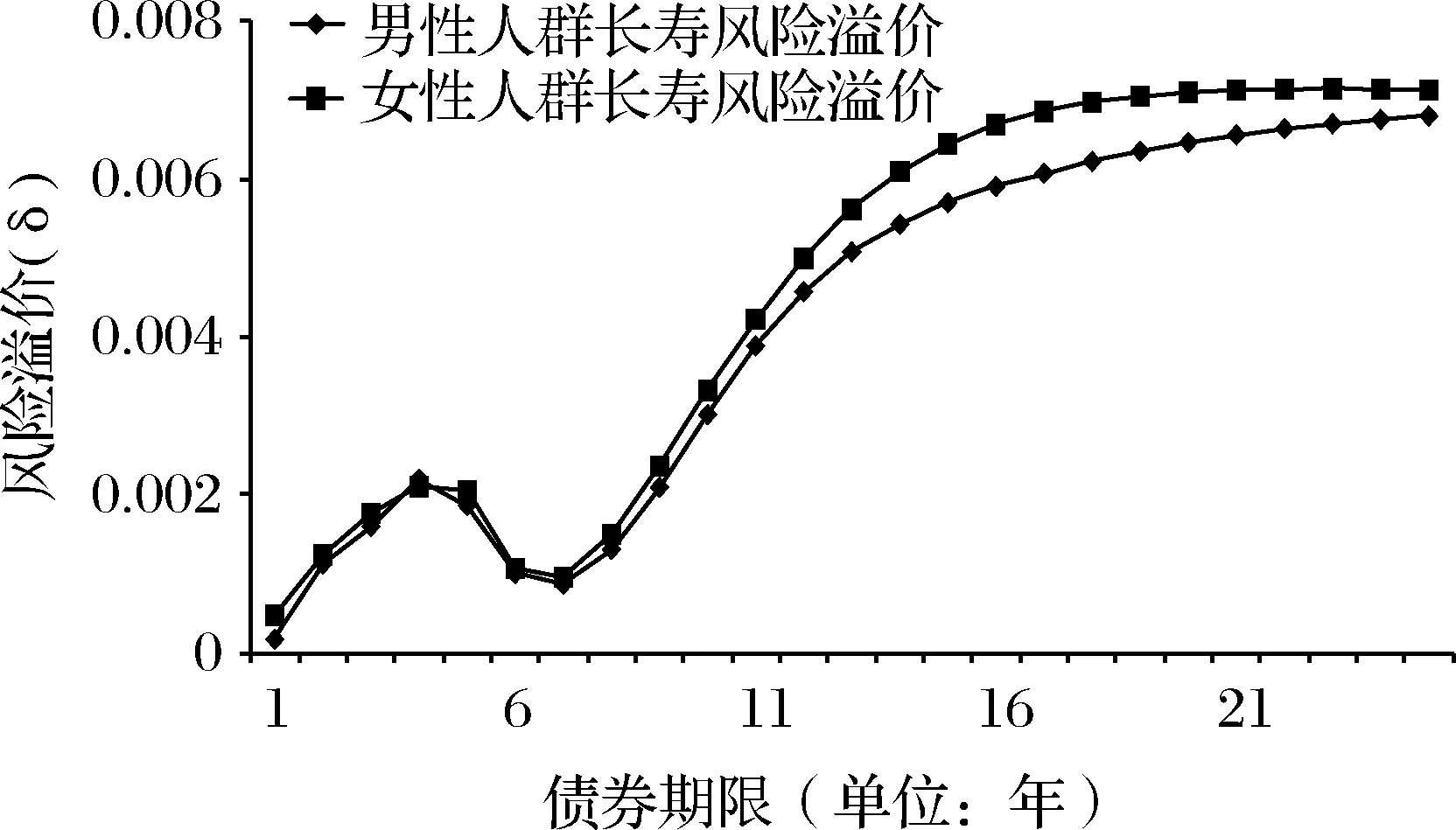
图6 KL相对熵计算的风险溢价(m=6)

从图6中可以看出，融合多个风险溢价信息的情况下，无论从不同性别角度，还是从不同期限角度去分析，长寿债券所显示的风险溢价都已有了显著变化。无论是以男性人群还是以女性人群的生存指数为定价标的，风险溢价与债券期限的关系均呈N型，即风险溢价在较短期限范围内会呈现极大值和极小值，与仅包含单一资产信息情形差别较大。这也是由于新加入的资产信息的约束造成的。从不同性别来看，男性和女性长寿风险的市场价格信息是有差别的，女性长寿风险的市场价格要略高于男性，这种表现尤其在期限较长的债券中更为明显。这表明，女性长寿风险面临的不确定性更明显，因而市场会要求更多的风险溢价，特别是当债券的发行期限逐渐增长时，女性长寿风险溢价与男性长寿风险溢价的差距更明显。

在图7和图8所展示的分别使用Tsallis相对熵和Rényi相对熵定价的结果来看，基本上也体现了相似的性质。所不同之处表现在，使用Tsallis相对熵和Rényi相对熵进行定价，不同性别的风险溢价体现的差异更加明显，而当α和q的大小趋近于1的时候，Tsallis相对熵和Rényi相对熵的定价表现又接近于KL相对熵，证明了定价结论的稳定性。

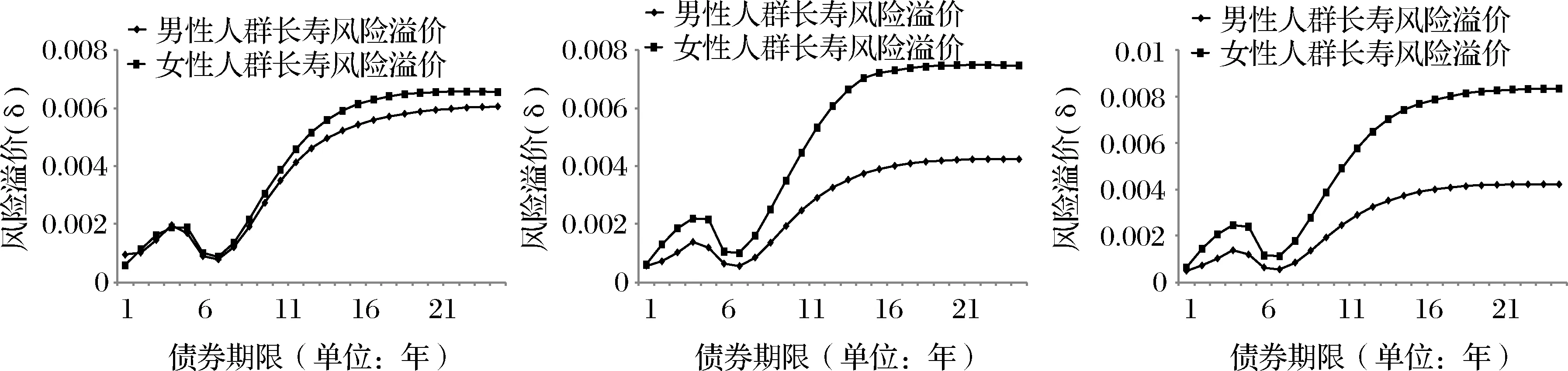
图7 Tsallis相对熵得到的风险溢价(m=6)

图8 Rényi相对熵得到的风险溢价(m=6)

同时，通过比较只考虑单个风险市场价格信息和考虑多个风险市场价格信息的情形，我们也发现，使用相对熵方法进行定价，其结果对于市场中所能提供的证券数目较为敏感，体现在m=1和m=6两种情形下，债券风险溢价随期限变化而差别巨大。这主要是由于随着资产数目的增加，也为整个市场提供了更为丰富的信息，而新信息的加入又必然会影响到风险中性测度的选择，从而最终影响到债券风险溢价的表现。这也体现了相对熵方法的可塑性，即随着市场完全度的提高，市场能够提供的风险价格信息越丰富，债券的定价也将越来越合理。由此可见，增强长寿风险管理能力，并不等价于一味地改进定价技术和模型，一个健全稳定的金融市场反而更能从根本上为长寿风险管理提供巨大的支持。

6 结语

本文在使用CBD模型对我国男女人群死亡率进行模拟的基础上，结合相对熵方法，对我国EIB/BNP型长寿债券进行了定价。定价的过程中，本文尽可能地搜集了金融市场的风险市场价格信息，使定价结果能够更贴近我国的实际情况；在定价方法上，选择不同的相对熵进行比较研究也保证了结论的稳健性。同时本文以性别人群为研究对象进行了定价，结果发现女性的长寿风险不确定性更高。本文的研究也证明了应该如何使用长寿债券进行长寿风险管理。在拥有了高龄人口人年龄的历史死亡率数据的观测值之后，运用本文所展示的方法，可以解决长寿衍生品的定价难题。但本文的研究模型也依赖于对现有金融市场信息的获取，准确而丰富的市场信息获取将使得定价更为合理。因此，对于长寿风险的管理，除了要在技术和产品上进行创新之外，还需要促进金融市场健康持续的发展，发达的金融市场将提供更丰富的产品信息，为长寿风险的管理提供有力的支撑。