带预算约束的广告主均衡报价研究
——基于纳什均衡角度
2019-06-04刘树林
韩 帅,刘树林
(1.山西财经大学国际贸易学院,山西 太原 030006;2.对外经济贸易大学国际经济贸易学院,北京 100029)
1 引言
随着全球信息产业的高速成长,截至2017年6月,我国互联网用户规模已达到7.51亿,稳居世界第一,2017年上半年新增用户数量1992万,互联网普及率达到54.3%,比2016年底提升1.1%,预计2017年底我国互联网用户数量将达到7.72亿,互联网普及率将到达55.9%。在这个信息爆炸的时代,广大网民对于所获信息的准确度需求也在逐步提高。党的十九大报告指出,我国社会的主要矛盾已经转化为人民日益增长的美好生活需求和不平衡不充分的发展之间的矛盾。传统的信息获取方式已很难满足人们的需求,网络搜索的重要性也愈发显著。关键词广告作为搜索引擎向网民投放广告的一种途径,已成为互联网企业重要的盈利模式之一。大量的广告主把部分广告费用投资到搜索引擎,以便在更大范围内宣传和销售自己的产品及服务。在美国当地时间2017年10月27日,国际知名搜索引擎Google的母公司Alphabet发布了截至2017年9月30日的第三季度财报。内容显示,Alphabet今年第三季度总营收为277.72亿美元,同比增长24%,净利润为67.32亿美元,较去年同期的50.61亿美元,同比增长28%。而该公司的主要收入来源为在线广告营销服务,实际情况也表明互联网广告对于互联网企业获取利润的重要影响不言而喻。关键词广告是在线广告的重要组成部分,而关键词拍卖作为关键词广告的出售模式,有必要对其进行理论研究。
关键词拍卖的早期研究多集中在拍卖机制设计及改进方面,并没有考虑广告主有预算约束的情况。Varian[1]最先将博弈论引入关键词拍卖领域,给出关键词拍卖模型的纳什均衡(Nash Equil-ibrium, NE)和对称纳什均衡(Symmetric Nash E-quilibrium, SNE)的定义及相关性质,还指出搜索引擎在广义第二价格(Generalized Second Price, GSP)拍卖机制下的收益不低于在Vickrey-Clarke-Groves(VCG)机制下的收益。而Edelman等[2]进一步研究了GSP机制,证明说真话(报价等于估价)不是GSP机制的占优策略,并给出局部无嫉妒均衡(Locally Envy-Free Nash Equilibrium, LEFNE)的概念,证明局部无嫉妒均衡与SNE是等价的。这两篇论文是最早研究关键词拍卖的文献,属于本领域的奠基性工作。在此基础上,Bu Tianming等[3]认为广告主可以同时提交多个报价,分析了该情形下满足纯策略纳什均衡的条件。Fukuda等[4]借鉴Edelman的方法,使用LEFNE研究VCG机制,并给出该机制下广告主均衡报价的区间。为了获取最大社会福利,Yuan Yong等[5]研究了广告主的合作式稳定型报价策略,应用进化博弈理论与合作进化模拟于重复关键词广告拍卖,发现“友好”报复策略可以促使竞争广告主间形成稳定的合作机制。Thompson和Leyton-Brown[6]针对主流搜索引擎大多采用加权GSP机制销售关键词广告位的现象,提出一种“计算机理分析”的方法,计算该模型的纳什均衡,并与其他三种位置拍卖模型及七种已有估计模型进行对比,发现wGSP在社会福利和预期点击数两方面的表现都是最好的。原全和汪定伟[7]基于广义第一价格拍卖,建立关键词拍卖的最优投标价格决策模型,并由此给出广告主获取最大期望收益时的报价。针对关键词拍卖中虚假广告泛滥问题,殷红[8]在GSP机制中引入广告主信誉度,建立可信竞价排名机制。当广告主信誉度差别很大时,改进机制在搜索引擎收益和拍卖效率方面的优势显著。用户兴趣度对点击率也有较大影响,董红斌等[9]在GSP机制中引入兴趣度因子,建立基于兴趣度的拍卖模型,对于点击数、搜索引擎收益的范围以及拍卖配置效率均有小幅提高,但损失了部分运行效率,等价于用时间换取收益。
随着该领域研究不断深入,部分学者开始关注广告主预算对关键词拍卖的影响。Abrams等[10]使用线性规划的方式,研究了考虑预算的广告主最优收益问题。Chen Ligang和Li Yijun[11]对于广告主选择不同搜索引擎及如何进行预算分配的问题进行分析,指出应依照不同目标对预算进行合理分配。Hafalir等[12]提出一种Sort-Cut拍卖机制,研究了特征相同关键词的多轮拍卖问题,广告主不能通过低报预算或保守估价获益,但是高估预算和估价可以提高收益。Muthukrishnan等[13]从概率角度建立预算优化模型,并通过该模型预测网民检索行为数据的概率分布状况。Gummadi等[14]应用马尔科夫决策法分析带预算广告主的竞价问题。Cholette等[15]采用概率方法,找到广告主支付不超过预算的最优报价。Koh[16]基于SNE,建立考虑广告主预算约束的关键词拍卖模型,给出并证明了广告主提高报价后无利可图的充要条件,通过实例说明降低报价后收益变化是不确定的,由此得出报价向量是带预算约束的SNE条件,最后分析了在一个理想环境下,搜索引擎的收益情况以及两位广告主组成的报价向量是非占优策略均衡的条件。Zhang Jie等[17]研究了广告主报价和每日预算的动态调整,避免预算浪费在早期无效点击上,以获取更好的广告投放机会。Arnon和Mansour[18]将重复性付费搜索广告拍卖看作单次博弈行为,并称为预算拍卖,其中每位广告主需要提交一个报价和预算,使用序贯第二价格拍卖机制出售广告位,发现当广告主报价不高于估价,该博弈存在纯策略纳什均衡。杨彦武等[19]从跨搜索引擎与时间序列的角度,研究关键词拍卖中的预算分配与调整问题,构建出能够提高分配效率的策略模型。于洪雷等[20]将广告主按估价和预算分布进行分类,分别从长期与短期角度建立模型,研究预算约束下GSP机制的均衡投标策略问题,得到静态与动态环境下关键词拍卖的均衡点。杨雪等[21]基于预算约束限制,首次构建形式化的视频广告拍卖模型,与关键词拍卖类似,该模型不限制参与竞拍者的边际效用形式。通过对比三种线性收益函数和一种非线性收益函数,证明改进机制收益和社会效用的有效性,并分析不同预算约束对机制的影响。与国外发展情况相比,国内研究带预算约束的关键词拍卖文献较少,还处于起步阶段。
综上所述,已有的关键词拍卖研究存在以下不足:首先,许多研究未考虑广告主的预算约束,但在实际情况中,即使是市值很高的大企业,它的广告预算也是有限的,广告主需要事先制定关键词广告的投标策略。因此有必要从理论上对该问题进行深入分析。其次,由于SNE条件的一致性,现有研究带预算约束问题的文献,主要采用该均衡条件。当今主流搜索引擎均使用GSP机制,但是GSP的缺陷在于任意广告主维持在原位不向上偏离的不等式不符合GSP机制,相较下NE条件符合该机制[22]。最后,2017年底召开的中央经济工作会议中已提出,我国经济发展进入新时代,基本特征是我国经济已由高速增长阶段转向高质量发展阶段。而高质量的发展就需要企业提高经营效率,合理使用预算资金,从而达到效用最优。因此,利用NE概念研究如何合理地利用预算更具有应用价值。
鉴于此,本文受Koh[16]的启发,使用NE概念研究预算约束下广告主的均衡报价问题,分别从报价向上偏离和向下偏离两方面进行分析,给出了广告主报价达到均衡时所应满足的充要条件。这将有助于广告主进行预算的合理分配,给出最优报价,从而获得最大收益。本文与之前研究的主要区别在于:第一,本研究基于NE分析带预算约束的广告主达到均衡报价的条件,相比SNE更符合实际情况。第二,本研究根据NE条件推导出满足NE的广告主报价的上下界,并与SNE的上下界进行了对比。第三,本研究给出了报价向量达到带预算约束的纳什均衡时应满足的条件。相比不考虑预算约束的情况,带预算约束的情况要复杂的多,需要从报价偏离的角度得出结论,并阐述了此均衡条件的实际意义。
2 模型建立
2.1 基本模型
假设模型中有n位广告主竞争获得s个广告位,其中n≥s,由广告主构成的集合为N={1,2,…,n},而广告位组成的集合为S={1,2,…,s}。该模型的保留价为0。广告主j的估价、报价、支付与收益分别为vj,bj,pj与πj,其中j∈N。cj表示在单位时间内广告位j获得的点击数,其中j∈S。由网民浏览习惯可知,不同广告位对网民的吸引力由上到下严格递减[22],有c1>c2>…>cs,而且仅有s个广告位,故cs+1=cs+2=…=cn=0。
下面对每位广告主重新进行编号,以便于后续表述。获得广告位j的广告主的报价记为bj,估价为vj。本研究中广告主支付使用GSP机制,且该模型是完全信息的,即所有cj,bj,vj都是已知的。因此,广告主j的支付满足pj=bj+1,收益为πj=cj(vj-bj+1)。
下面回顾Varian构建关键词拍卖的两种不同均衡[1]。
定义1 若所有参与竞拍的广告主的报价构成的向量b=(b1,b2,...,bn)满足以下条件:
cj(vj-bj+1)≥cl(vj-bl+1),∀l>j
(1)
cj(vj-bj+1)≥cl(vj-bl),∀l (2) 则称报价向量b是NE。 定义2 若所有参与竞拍的广告主的报价构成的向量b=(b1,b2,…,bn)满足以下条件: cj(vj-bj+1)≥cl(vj-bl+1),∀l,j (3) 则称报价向量b是SNE。 通常满足NE的报价向量很多,故采用BNE表示报价向量是NE的集合。同理,采用BSNE表示报价向量是SNE的集合。两个集合均未考虑广告主的预算。从定义可以看出,NE与SNE的主要区别是任意广告主j报价不向上偏离的条件。 为了简便,令竞拍全程时间为1,例如实际中的1天。假设广告主j为理性人,显然他的报价不会超过估价,从而有vj>pj=bj+1。 定义3 假设广告主j的报价为bj,获得广告位θ(j),支付为pj,其预算给定为Bj,参与竞拍的时间为tj,其中j∈N。若报价向量b=(b1,b2,…,bn)满足: (1)b∈BNE; (2)如果广告主j的支付pj≤Bj,则其参与竞拍的时间tj=1,即全程占据广告位θ(j),其中j∈N; (3)如果广告主j的支付pj>Bj,则其参与竞拍的时间tj=Bj/pj<1,将提前退出竞拍,其中j∈N; (4)对任意广告主k(k≠j),bk都不改变。广告主j的报价向上偏离占据靠前广告位后收益没有增加,向下偏离占据靠后广告位后收益也没有增加,其中k,j∈N。即模型中任意广告主报价bj向上偏离后无利可图,并且bj向下偏离后同样无利可图,则称该向量b是带预算约束的纳什均衡(Nash Equilibrium with Budget Constraint, NE-B)。 下面用数例解释引入预算后对拍卖模型的影响。 例1 考虑3位广告主竞拍2个广告位的情况。详细信息如下表。 表1 信息列表 图1 带预算广告主所在广告位点击数受报价变化的影响 从图1可以看出,广告主2提高报价后,在时期[0,0.5],广告主1占据首位,广告主2位居次席;在时期[0.5,1],广告主1提前退出,广告主2占有广告位1,广告主3占据广告位2。由于广告主2的全程支付价格p2=0.5c2b3+0.5c1b3=1.5 该结果表明考虑预算约束会使广告主产生改变自身报价的动机(收益增加)。 本文研究的是基于纳什均衡的带预算广告主的均衡报价问题,而得到在此均衡下广告主报价的取值边界有助于分析报价向量达到NEB应满足的条件。 首先将定义1中的两个不等式分别进行化简,则报价bj应满足: (4) (5) (6) 根据式(4)可以得到满足NE条件的报价向量中bj的上下界。 (7) 证明:由于报价向量b∈BNE,所以式(1)成立。令l=j+1,可得: cj(vj-bj+1)≥cj+1(vj-bj+2) 化简得: bj+1≤(cj-cj+1)vj/cj+cj+1bj+2/cj 由此推导可以得到: bj≤(cj-1-cj)vj-1/cj-1+cjbj+1/cj-1≤(cj-1-cj)vj-1/cj-1+cj[(cj-cj+1)vj/cj+cj+1bj+2/cj]/cj-1 继续递推可得: bj≤(cj-1-cj)vj-1/cj-1+(cj-cj+1)vj/cj-1+…+(cs-1-cs)vs-1/cj-1+csbs+1/cj-1 (8) 令式(4)中j=s+1,并且cs+1=0,则广告主s+1的报价满足: (9) 将式(9)代入式(8)整理: 综上,定理1得证。 (10) 证明:由于报价向量b∈BNE,故式(2)成立。令l=j-1,可得: cj(vj-bj+1)≥cj-1(vj-bj-1) 化简得: bj-1≥(cj-1-cj)vj/cj-1+cjbj+1/cj-1 由此推导可以得到: bj≥(cj-cj+1)vj+1/cj+cj+1bj+2/cj≥(cj-cj+1)vj+1/cj+cj+1[(cj+2-cj+3)vj+3/cj+2+cj+3bj+4/cj+2]/cj>(cj-cj+1)vj+1/cj+cj+2[(cj+2-cj+3)vj+3/cj+2+cj+3bj+4/cj+2]/cj, (cj+1>cj+2>0) 继续递推下去。当s与j奇偶性相同时,报价bj满足: bj≥(cj-cj+1)vj+1/cj+(cj+2-cj+3)vj+3/cj+…+(cs-2-cs-1)vs-1/cj+cs-1bs/cj (11) 令式(4)中的j=s,并且cs+1=0,则广告主s的报价满足: (12) 将式(12)代入式(11)整理得: bj≥(cj-cj+1)vj+1/cj+…+(cs-2-cs-1)vs-1/cj+cs-1vs+1/cj>(cj-cj+1)vj+1/cj+…+(cs-2-cs-1)vs-1/cj+csvs+1/cj, (cs-1>cs>0) 同理,当s与j奇偶性相异时,bj满足: 综上所述,定理2得证。 定理1与2给出了NE条件下报价的理论取值范围,该结论为研究带预算广告主的均衡报价策略提供了理论基础。 本节分析报价向量b∈BNE达到NEB时广告主应具备的条件。研究将分别从不同方向的报价偏离着手,首先考察报价向上偏离的情形。 定理3任意报价向量b∈BNE,预算Bj对所有广告主j∈N都满足cjbj+1≤Bj,则任意报价bj(1 (1)当Bj≥cj-k+1bj-k+1,广告主j将始终占据第j-k+1位,其收益为πj=cj-k+1(vj-bj-k+1)。 假设式(2)中l=j-k+1,得到cj(vj-bj+1)≥cj-k+1(vj-bj-k+1),所以此时广告主j的报价向上偏离后无利可图。 (2)当Bj 同理,令式(2)中l=j-k+1,有cj(vj-bj+1)≥cj-k+1(vj-bj-k+1)≥cj-k+1t(vj-bj-k+1)。这说明预算不足时,广告主j的报价向上偏离也无利可图。故定理3充分性证毕。 (必要性)假设报价向量b∈BNE,对所有j∈N有cjbj+1≤Bj。下面使用反证法。假设广告主j的预算Bj 广告主j+1在第j+1位的时间为t,而上升一位后占据第j位的时间为t′-t,其中t′满足[cj+1t+cj(t′-t)]bj+2=Bj+1,可能大于1。由于采用GSP机制,广告主j+1的支付需要分析广告主j+2所处的位置。 (1)广告主j+2占据第j+2位的时间为t,故广告主j+1占据第j+1位的支付为cj+1bj+2; Δπj+1=[cj+1t+cj(min{t′,1}-t)](vj+1-bj+2)-cj+1(vj+1-bj+2) 所以广告主j+1的报价向上偏离后收益增加,必要性得证。定理3证毕。 定理3揭示了当报价向量满足NE条件时,任意一位广告主提高报价无利可图应满足的充要条件。由定理3可以看出,广告主j的预算至少需要达到cjbj,否则其向上偏离后将获得的更大收益。由该定理将逐步分析出广告主报价达到NEB时需要满足的条件。 该推论运用定理3的结论,当广告主预算较低时,后一位广告主提高报价是有利可图的,所以此时报价向量不满足NEB条件。该结论说明当某位广告主制定的广告预算较少时,排名靠后的广告主将有动机提高报价竞争该广告位,以获取更高收益。因此,广告主们的预算分配过少将导致无法达到NEB。 下面从实例角度,验证定理3的结论。 例2 构建一个拍卖模型,其中4位广告主竞争3个广告位。模型信息如表2所示,其中预算Bj≥cjbj,(j=1,2,3)。 表2 报价向量信息列表 (1)验证该报价向量b∈BNE。 广告主1在不同位置: c1(v1-b2)=108>c2(v1-b3)=48>c3(v1-b4)=20>c4(v1-b5)=0。 可知b1满足NE条件。 同理,可以验证b2,b3,b4均满足NE条件,但不满足SNE条件。因此,该报价向量b=(b1,b2,b3,b4)∈BNE。 (2)验证定理3的充分条件。以广告主2为例,由于预算满足Bj≥cjbj,(j=1,2,3),则广告主2报价向上偏离无利可图。 广告主2在第2位的收益: π2=c2(v2-b3)=6×(9-4)=30。 当b2向上偏离到第1位时,由于预算B2=66 即b2向上偏离后收益增加,定理3的必要条件成立。 对于广告主报价向下偏离的收益变化情况,首先利用实例结果进行说明。 例3 同样采用例2的相关数据。先计算NE下所有报价的边界。 表3 报价向量信息列表(边界) 先验证该报价向量b∈BNE。广告主1在不同位置: c1(v1-b2)=144>c2(v1-b3)=54>c3(v1-b4)=24>c4(v1-b5)=0。 可知b1满足NE条件; 而广告主2在不同位置: c2(v2-b3)=36>c1(v2-b1)=18=c3(v2-b4)=18>c4(v2-b5)=0, 而c1(v2-b2)=90>c2(v2-b3)=36。 可知b2满足NE条件,但不满足SNE条件。 同理可验证b3,b4均满足NE条件,但不满足SNE条件。故该报价向量b=(b1,b2,b3,b4)∈BNE。 c1(v1-b2)=24≥c2(v1-b3)=24>c3(v1-b4)=12>c4(v1-b5)=0。 可知b1满足NE条件。 同理可知b2,b3,b4均满足NE条件,并且b4也满足SNE条件。因此,该报价向量b=(b1,b2,b3,b4)∈BNE。 (4)情形(2)和(3)中b取值不同,将对b1向下偏离产生不同影响。 对于情形(2),初始时广告主1的收益为π1= 因此,情形(2)中b1向下偏离无利可图; 因此,情形(3)中b1向下偏离有利可图。 以上两种情形中,广告主1的收益变化产生差异的原因有两点:第一,b1降低至第2位,从而导致所占位置的点击数减少(c2t+c1(1-t) 例如情形(2),由于广告主2参与竞拍时间(t=11/12)较长,尽管广告主1在第2位时单次点击收益增加,但点击数的损失更大,故其收益下降;对于情形(3),广告主1在第2位的时间(t=11/32)较短,在广告主2退出后,他所在广告位的点击数恢复至第1位的水平,并且剩余竞拍时间较长,致使其收益增加。 定理4若广告主j(j∈N)的报价bj向下偏离,其收益将由所在广告位点击数与单次点击收益共同决定。广告主j的收益变化取决于两者中占优因素的变化趋势。 由例3的分析可以看出,广告主报价bj向下偏离的情况比较复杂,在此情形下准确描述广告主的收益变化较为困难。下面将从侧面角度研究报价向量b达到NEB应满足的条件。 由于cjt+(1-t)cj-1>cj,故上式中不等式成立。 该引理的结论与4.1节中推论类似,如果报价向量b中某位广告主设置的广告预算较低,则b将不满足NEB。 ∈BSNE,即: (13) 广告主j的初始收益可转化为: 同理,由式(7)可得,广告主j报价向上偏离一位(第j-1位)后的支付: 因此,式(13)对l=j-1,j+1均成立。引理2得证。 因此,报价向量b∈BNE是NEB。充分性成立。 综上,定理5得证。 纳什均衡是博弈论中最重要的理论之一,为现代经济理论的发展奠定了坚实的基础。早期关于关键词拍卖的研究,为了便于分析,几乎不考虑有预算约束的情况,而且多数没有从纳什均衡角度研究。但在实际情况中,广告主在搜索引擎网站投放关键词广告必须考虑预算约束。因此,本文重点研究了带预算约束的关键词拍卖问题。主要结论可归纳为以下三个方面: (1)推导出基于NE的广告主报价边界,并与SNE条件下的报价的边界进行对比,发现两种均衡下的报价上界相同,而下界大小取决于排序j的大小。这是由于NE中不向下偏离条件与SNE相同,而不向上偏离条件不同所导致的。 (2)预算对于报价向量达到NEB具有显著影响。广告主只有具备充足的预算才能够持续参与竞拍,否则就要提前退出。此外,由于GSP机制的特点,若某位广告主预算分配较少,排位较低的广告主出于提高自身收益的目的,也会产生向上偏离的动机。通过研究发现,带预算的广告主向上偏离无利可图除了需要满足NE条件外,预算Bj也不能低于cjbj。而向下偏离的情况较为复杂,广告主的收益变化取决于所在广告位点击数与单次点击收益两者占优因素的变化趋势。 本文的主要创新在于:第一,基于NE条件,在关键词拍卖中引入广告主预算这一影响因素建立模型。通过对比Koh[16]研究SNE中带预算约束的关键词拍卖模型,发现其中不向上偏离的不等式右侧广告主的支付价符合第三价格拍卖机制(pj=bl+1,∀l 鉴于带预算约束的关键词拍卖涉及的问题较多,本研究还存在着三个方面的不足。第一,实际中关键词拍卖的情况更为复杂,很多参数和假设条件都不固定,例如广告主的数量、广告位数等,本文的假设与实际情况还存在一定差距,今后可以调整假设条件,使研究结果更符合实际。第二,本文结论的前提条件是完全信息博弈,而任意一位广告主进行决策时,往往无法获得其他外界的信息,未来可以通过概率分布的方式将研究拓展到不完全信息模型中。第三,受选题限制,本文仅从广告主角度对带预算约束的均衡报价问题进行研究,后续研究可以从搜索引擎的角度分析在带预算约束的纳什均衡下,预算约束对搜索引擎收益的影响,以及搜索引擎如何改进机制设计可以使社会效率提高等问题。2.2 改进模型



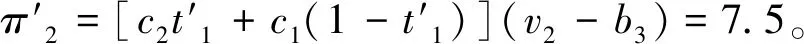
3 基于纳什均衡的广告主报价边界




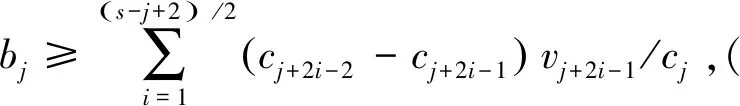
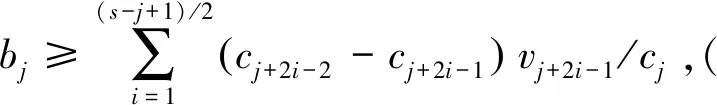
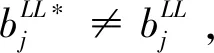
4 带预算约束的纳什均衡
4.1 报价向上偏离




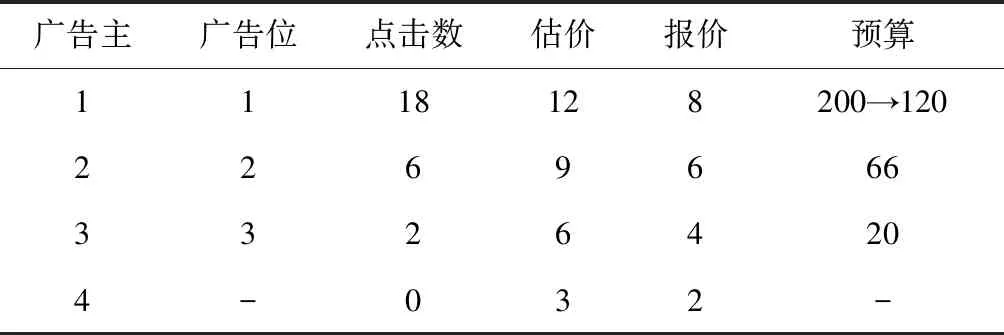


4.2 报价向下偏离
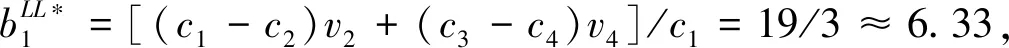
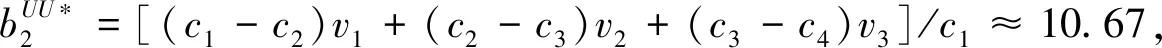


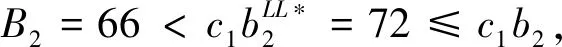



4.3 均衡条件



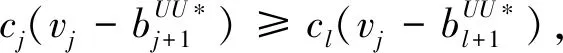





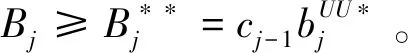
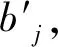

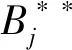
5 结语

