基于未来效率的兼顾公平与效率的资源分配DEA模型研究——以各省碳排放额分配为例

王 荧,王应明

(1.福建江夏学院金融学院，福建 福州 350108；2.福州大学经济与管理学院，福建 福州 350108)

1 引言

评估各生产决策单位(Decision Making Unit，DMU)的投入产出效率及改进潜力，可以为经济分析、管理决策提供重要参考。Farrell[1]在1957年首创了现代效率的测度技术：首先，构建DMU的生产前沿面，其次，测算DMU的实际投入产出点顺着某一路径改进至生产前沿面的距离作为的该DMU的效率改进空间。该测算技术的前提是要获知DMU的生产前沿面。Farrell[1]认为可以使用两种方法来构建生产前沿面：参数型模型法和非参数的数据包络法(Data Envelopment Analysis， DEA)。

在提出之后，非参数的DEA方法没有马上得到多数学者的认可。直到1978年，Charnes等[2]提出的不变规模报酬模式下的CCR模型，DEA方法才得到学术界普遍关注。随后，Banker等[3]提出生产规模收益可变的BCC模型。迄今为止，CCR模型和BCC模型是应用最广泛的传统DEA模型。不过，CCR模型和BCC模型均假设产出仅为期望产出，忽略了现实经济中，除了期望产出外，产出往往还包括废水、废气、固废等非期望产出。因此，需要对传统DEA模型进行拓展。现有文献主要提出三种思路解决非期望产出[4-6]：(1)将非期望产出当作投入处理[4-5]。(2)以“非对称”方式处理各种产出，例如，采用曲线测度法[6]、方向距离函数法[7]、多阶段DEA模型[8-9]、SBM模型[10]等方法模型，实现增加期望产出的同时，减少非期望产出。(3)数据转换函数法[11]，例如，采用取倒数等数学变换法，人为地将越小越好的非期望产出转换成越大越好的“期望产出”。

DEA方法可以得到与经典的边际分析完全相似的结论[12]。因此，近年来，许多文献将DEA方法的应用从效率评价拓展到资源分配。现有文献中，资源分配的DEA模型主要有四种:(1)固定成本分配的DEA模型[13-15]。(2)中央化资源分配的DEA模型[16]。(2)零和博弈DEA模型[17]。(4)资源配置的参数DEA模型，包括了HFM-DEA模型[18]、SFM-DE模型[19]、ASFM-DEA模型[20]、EFM-DEA模型[21]等。

总体而言，对于效率评价和资源分配的DEA模型的研究，现有文献已经取得了不少成果，但也还存在一些问题需要进一步解决。

首先，现有DEA模型大都根据以往的数据，对各DMU进行效率评价，并在此基础上进行资源分配。但是，过去的DEA效率并不代表未来时期的DEA效率。假设，当前时间为第t期，现在需要分配未来第t+1期的资源，根据经济学原理，应该要根据各DMU第t+1期的效率进行分配，才能实现第t+1期的最优资源分配。为此，本研究首先根据历史数据计算每个生产决策单元过去各期的技术增长率，并预测各DMU未来的技术增长率，进而获得未来的生产前沿面和生产可能性区域，从而为下文的基于未来效率的资源分配的DEA模型奠定基础。

其次，现有的DEA模型，大都通过使各DMU移动到生产前沿面，从而实现最优的效率和资源分配[22]。然而，这样的效率评估与资源分配显得相对狭隘，对于实际的管理运用也相对有限。因为，现实经济中，管理往往都是为了实现一定的期望目标，因此，管理者更希望评估各DMU的实际投入产出距离期望目标还有多大的效率改进空间，在此基础上进行资源分配。Lozano等[16]构建资源分配的DEA模型，实现了一定程度的多目标导向的资源分配：该DEA模型涉及的目标包括最大化总的期望产出、最小化总的可变要素投入和最小化总的非期望产出等三个，管理者可以调整三个目标的优先顺序进而形成不同的资源分配方案。尽管如此，在现实管理中，该DEA模型依然难以满足管理者的各种目标追求。因为，现实中，管理者未必总是希望每个子目标都要实现最优化，而是希望某些子目标实现一定程度优化的基础上，使另外一些子目标实现最优化，例如，管理者可能希望总的可变要素、总的非期望产出实现一定程度的缩减下实现总的期望产出的最大增长和最优配置。另一方面，管理者追求的目标往往是比较复杂的多目标——不只追求经济技术上的最优，而且往往也要兼顾诸如社会公平等目标。为此，本研究参考Lozano等[16]提出的DEA模型，基于测算出的未来的生产前沿面，构建了基于未来效率的兼顾公平与效率的资源分配的DEA模型。

该模型赋予管理者充分的灵活度来预先设定各种目标，具体包括九个硬性目标和三个软性目标。其中，硬性目标是指必须要满足的目标，三个针对各DMU的投入产出、三个针对全部DMU的投入产出总量、三个针对各种投入产出分配公平，这九个硬性目标均可以按照管理者的期望设定不同的值。在九个硬性目标约束下，分三个阶段分别实现三个软性目标：最大化期望总产出、最小化非期望总产出、最小化要素投入。管理者不仅可以改变九个硬性目标的参数值，以及调整三个软性目标的优先顺序，而且还可以在每个步骤潜力评估的基础上，根据节能减排潜力通过改变三个软性目标参数，进一步设定合理的期望目标，从而形成各种目标导向的兼顾效率与公平的资源分配方案。最后，本研究将构建的DEA模型运用于我国各省碳排放额分配研究。

2 变量及生产可能性区域假设

资源分配问题可以描述为：要在生产可能性区间内和目标约束下，合理分配资源，进而尽可能实现管理者期望的目标。为了构建基于未来效率的资源分配的DEA模型，需要对模型中涉及的变量以及DEA模型的生产可能性区域的假设进行说明。

2.1 变量说明

假设，共有J个DMU，每个DMU的投入产出种类相同，即，有I种要素投入，其中，IF种为固定要素，I-IF种为可变要素；共有K+S种产出，其中，K种为期望产出，S种为非期望产出，其他相关变量的名称与含义具体见表1。

表1 相关变量的名称与含义

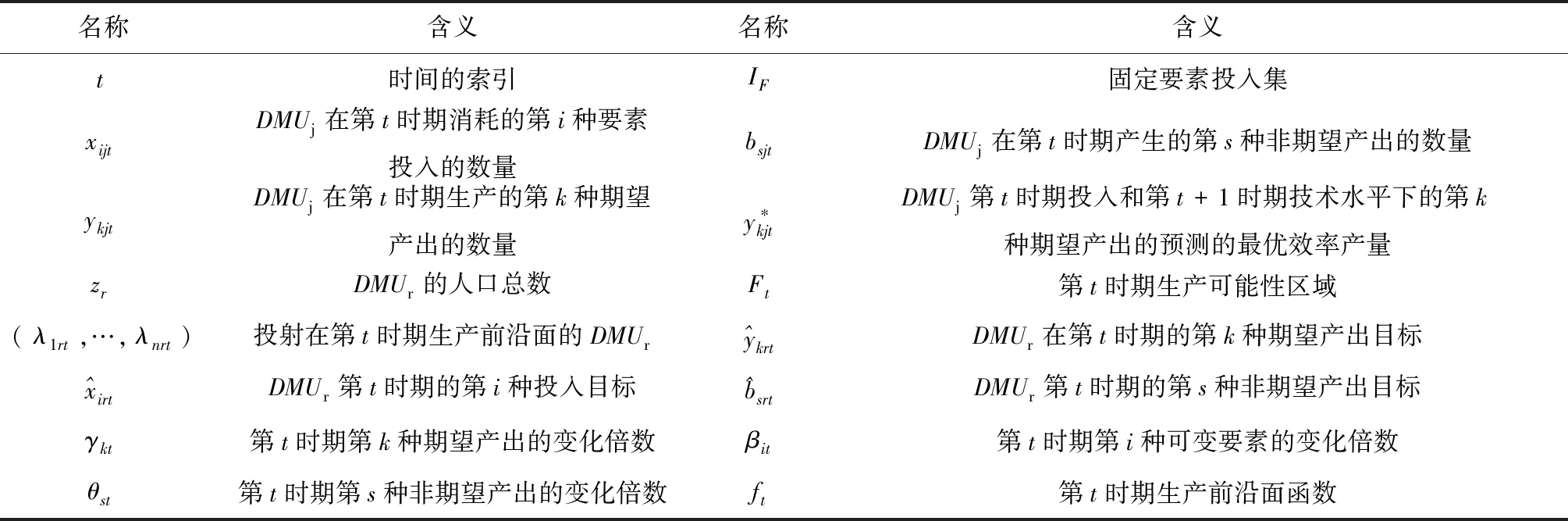
续表1 相关变量的名称与含义

2.2 生产可能性区域的特征假设

参考Adler和Volta[4]的研究，本文中的生产可能性区域的假设包括以下几个方面：

Ⅰxijt≥0,ykjt≥0,bsjt≥0 (∀i∀k∀s∀t)；

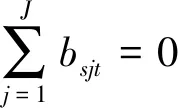
Ⅵ (ykjt,bsjt)∈Ft(Xt,Yt,Bt)⟹(θykjt,θbsjt)∈Ft(Xt,Yt,Bt)forall0≤θ≤1(∀t)；

Ⅶ (ykt,bst)∈Ft(Xt,Yt,Bt),yk′t≤ykt⟹(yk′t,ykb)∈Ft(Xt,Yt,Bt)(∀t)；

Ⅷλj≤1 ∀j。

其中，(Ⅰ)式的含义是：任何DMU的任何投入产出均不能小于零；(Ⅱ—Ⅳ)式的含义分别是：任何一种要素(产出)都至少被一个DMU使用(生产)，任何一个DMU都至少使用一种要素，都至少生产一种期望产出和一种非期望产出；(Ⅴ)的含义是：要没有非期望产出，则也没有期望产出，即，期望产出和非期望产出具有联合生产的性质；(Ⅵ)式的含义是：非期望产出具有弱可自由处理性；(Ⅶ)的含义是：期望产出具有强可自由处理性；(Ⅷ)规模收益可变。根据Kuosmanen[23]，同时满足(Ⅰ—Ⅷ)的生产可能性集合可以描述为以下的线性方程组(1)。

Ft=

(1)

3 未来效率的资源分配的DEA模型构建

3.1 构建总体思路

表2 模型中的硬性目标参数的名称与含义

3.2 基于未来效率的资源分配的DEA模型

3.2.1 目标参数说明

模型涉及的目标包括硬性目标和软性目标，具体参数的名称与含义见表2。其中，硬性目标是指必须要满足的目标，共有九个：三个是针对各DMU、三个是针对全部DMU的整体、三个是针对各种投入产出分配公平，这九个硬性目标均可以按照管理者的期望设定不同的值。不同公平原则，会有不同的公平含义与目标约束式，本文的公平原则：要尽可能使各DMU的各种投入(产出)的人均量都相等，均等于全国总的人均量。因此，本研究三个反映公平目标的约束式——使得各DMU的人均可变要素、人均期望产出和人均非期望产出与公平合理的人均量的偏离控制在合理的范围内。软性目标为尽量要实现的目标，共有三个：产出目标、节能目标和减排目标，每个软性目标都可以通过构建一个DEA模型予以实现。

3.2.2 基于未来效率的资源分配的DEA模型的构建

假设管理者的目标为：未来时期内，在管理者设定的硬性目标以及实现一定节能、减排目标前提下，最大化期望产出。可以通过构建模型(2)、模型(3)和模型(4)来实现这样目标追求下的资源分配。

第一阶段的模型(2)，主要用来评估未来效率和硬性目标约束下的总可变要素投入的节约潜力。模型(2)中，(2.1)—(2.2)为节能软性目标式；(2.3)—(2.6)为生产可能性集；(2.7)—(2.15)为硬性目标约束式。其中，(2.7)—(2.9)分别要求未来时期每个DMU的各种要素投入、各种期望产出和各种非期望产出均在管理者设定的范围内；(2.10)—(2.12)分别要求未来时期全部DMU的各种要素投入、各种期望产出和各种非期望产出控制在在管理者希望的范围内；(2.13)—(2.15)分别要求未来时期每一个DMU的分配公平状态控制在在管理者希望的范围内。由此可见，模型(2)评估了：未来时期，在九个硬性目标下，可变要素投入总量的最大节能潜力。

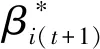
第二阶段的模型(3)，主要评估了未来时期内非期望产出的削减潜力: 与模型(2)相比，模型(3)有两处不一样：第一，(3.1)—(3.2)为减排软性目标式；第二，多了限制条件(3.16)：未来时期，每种可变要素总量都实现管理者希望的最小缩减目标。

(2.1)

(2.2)

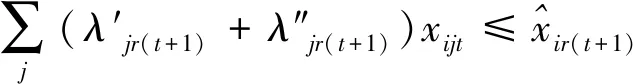
(2.3)

(2.4)

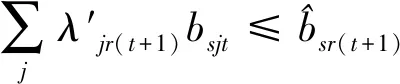
(2.5)

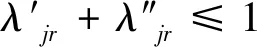
(2.6)

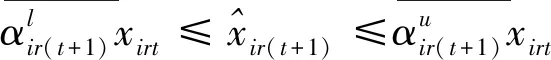
(2.7)

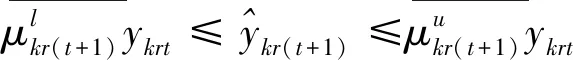
(2.8)

(2.9)

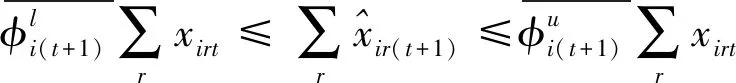
(2.10)

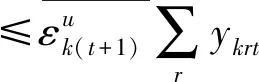
(2.11)

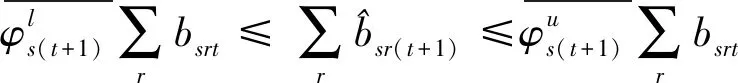
(2.12)

(2.13)

(2.14)

(2.15)

(∀i∀j∀k∀s∀r)

(3.1)

(3.2)

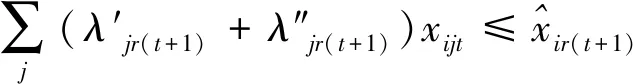
(3.3)

(3.4)

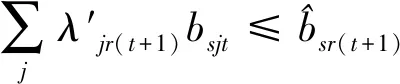
(3.5)

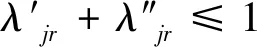
(3.6)

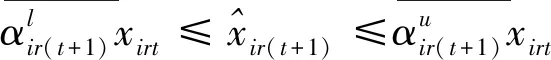
(3.7)

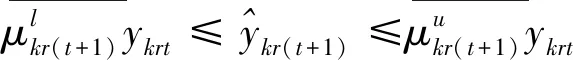
(3.8)

(3.9)

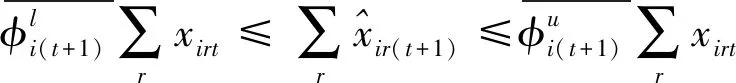
(3.10)

(3.11)

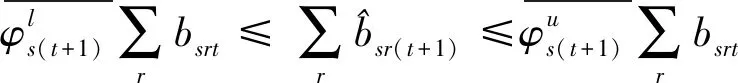
(3.12)

(3.13)

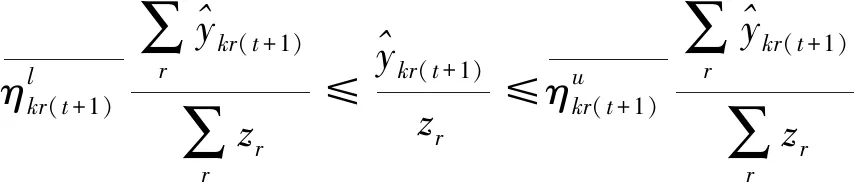
(3.14)

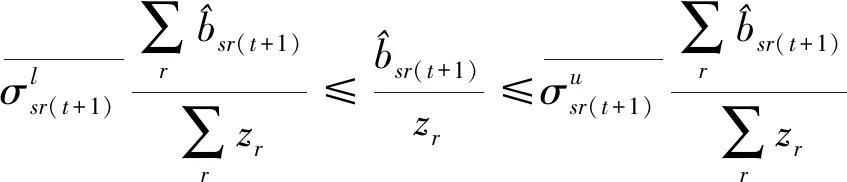
(3.15)

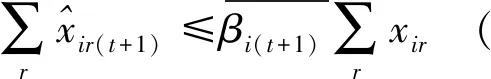
(3.16)

≥0 (∀i∀j∀k∀s∀r)

(4.1)

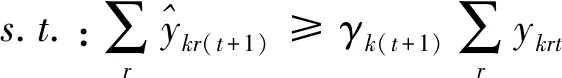
(4.2)

(4.3)

(4.4)

(4.5)

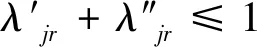
(4.6)

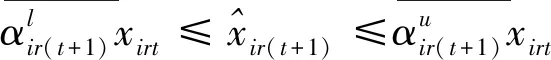
(4.7)

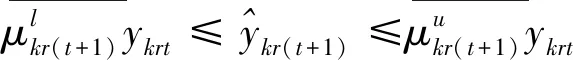
(4.8)

(4.9)

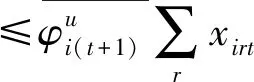
(4.10)

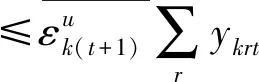
(4.11)

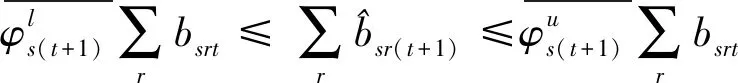
(4.12)

(4.13)

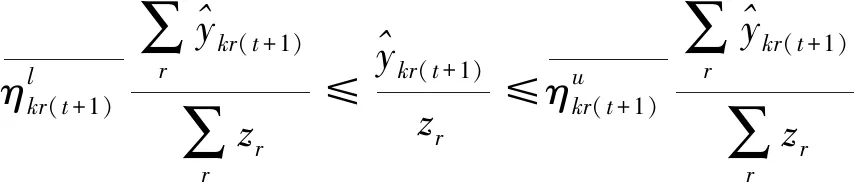
(4.14)

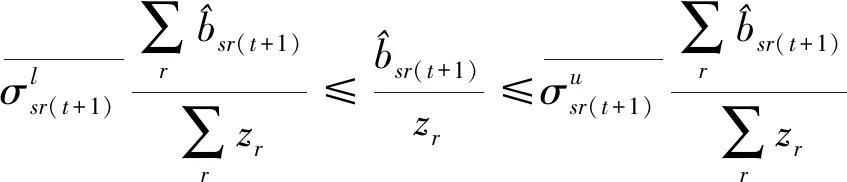
(4.15)

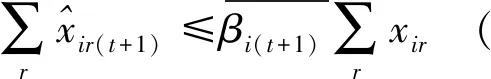
(4.16)

(4.17)

≥0 (∀i∀j∀k∀s∀r)

第三阶段：通过构建模型(4)，实现在管理者设定的硬性约束、总量上实现一定程度的节能减排等前提下总的期望产出最大化的目标。与模型(3)相比，模型(4)有两处不一样：第一，(4.1)—(4.2)为产出软性目标式；第二，多了限制条件(4.17)：未来时期，每种非期望产出总量都缩减至设定的最小缩减目标。

4 实证分析

4.1 实证思路

每个省区当作一个DMU。每个DMU的要素包括劳动投入、能源投入和资本投入等三种，分别用i=1、2、3作为其索引，其中，资本投入为固定要素；期望产出为GDP一种，用k=1作为其索引；非期望产出为废水排放总量、固体废弃物总量、碳排放总量等三种，分别用s=1、2、3作为其索引。由于数据的可得性，本研究将四川省和重庆市合并成未进行行政划分前的四川省，同时没有将西藏自治区、香港特别行政区、澳门特别行政区以及台湾省纳入分析，即，本研究的实证分析主要包含29个省区。

本研究将采集29个省区所有七个投入产出指标的2000年至2015年的数据，运用构建的基于未来效率的资源分配的DEA模型对我国各省的碳排放额进行分配。

4.2 数据说明

第一，劳动投入。由于我国缺乏平均工作时间的统计数据，因此，本研究以2001年至2016年的各省《统计年鉴》中公布的当年“就业人数”作为各省劳动投入数据。

第二，能源投入。除了2013年以外，采集2001年至2016年的《中国能源统计年鉴》中的“分地区能源消费总量”一值作为各省相应年度的能源投入。其中，2013年的数据采集自各省统计年鉴的“能源消费总量”一值。

第三，资本投入。运用“永续盘存法”[25]估算各省各年份资本存量。计算中所需数据来源与参数设定情况：资本折旧率取值为0.4[25]；采用张军等[25]测算的各省区2000年的资本存量作为初始资本存量；各年份各省固定资本形成额数据来自各年份的《中国统计年鉴》，并用固定资产投资价格指数折算成以2000年为基期的不变价格的数据。

第四，GDP。各省各年份的数据采集自各年的《中国统计年鉴》，利用平减指数折算成2000年为基年的不变价格的GDP。

第五，废水排放总量，采集自2001年至2016年《中国统计年鉴》。

第六，固体废弃物总量，采集自2001年至2016年《中国统计年鉴》。

第七，碳排放量。根据IPCC的《国家温室气体清单指南第二卷(能源)》第六章的估算公式来计算碳排放量。估算所需的参数设定以及数据来源情况：各种化石能源的能源净发热值的数据来源于《中国能源统计年鉴2013》附录4；根据IPCC的《国家温室气体清单指南第二卷(能源)》的表1.3设定各种化石能源的碳排放因子；将烟煤和无烟煤的碳排放因子按照8∶2的权重加权平均得到煤炭的碳排放因子，碳氧化因子设置为1；采用各省电能净消费量(电能消费量-电能生产量)来估算各省电能消费产生的碳排放量，同时，按照我国火力发电占比(78.05%)的折算比例将电能折算成标准煤(折算系数为0.1229千克标准煤/千瓦小时)，最后，根据每千克标准煤排放2.763千克二氧化碳的标准，估算出各省电能净消费导致的碳排放量。

4.3 预测方法的选择

基于每个省仅有15年的有限样本数据的事实，本研究拟通过比较分析，在指数平滑法、灰色预测法和ARIMA模型等三种适合小样本数据的预测方法中选一种用于测算各省区2001年至2016年各年的技术增长率。经过模式识别和检验，发现ARIMA模型为ARIMA(0，0，0)，即，实际上ARIMA模型用平均值作为预测值，效果较差，因此，本研究主要在指数平滑法和灰色预测法中进行选择。

通过表3的比较可以看出，指数平滑法的总平均相对误差为1.99%小于灰色预测法的2.41%。因此，本研究选择指数平滑法作为未来技术增长率的预测方法。

表3 主要预测方法预测各省技术增长率的相对误差比较

根据表3，运用指数平滑法预测各省技术增长率的平均相对误差都较小，其中，最大的是甘肃省，其平均相对误差为4.22%，最小是广东省，其平均相对误差为0.93%；最后，根据预测的未来时期技术增长率测算未来时期最优的投入产出数据。

4.4 目标设置说明

本实证分析主要为了说明本研究的DEA模型的实际运用，因此，本实证的目标设定仅作为一个特例，具体设置说明如下(具体参数设置见表4)。

表4 实证中的各硬性目标的说明

续表4 实证中的各硬性目标的说明

各省产出目标：未来时期各省区GDP不减少。

各省减排目标: 《中华人民共和国国民经济和社会发展第十二个五年规划纲要》明确要实现“化学需氧量、二氧化硫排放分别减少8%”，为了兼顾增长，因此将三废的最大削减幅度设置为目标的2倍，即最大削减幅度为16%；三废增长的上限设置为“十二五”期间全国三废的年均增长额，从而保证各省三废增长速度不超过“十二五”期间的年均增长速度。

各省节能目标：《中共中央关于国民经济和社会发展第十三个五年规划的建议》提出“能源资源开发利用效率大幅提高”， “十二五”期间全国能源投入年均增加5.65%，为了保证能源投入效率超过十二五水平，因此，将各省能源投入的增长上限设置为5.65%。和三废的设置理由类似，为了兼顾增长，能源投入减少不超过16%。“十二五”期间全国资本投入年均增加16.23%，“十三五”期间固定资本投资增长率将很难超过“十二五”，因此，将各省资本投入的增长上限设置为16.23%。

全国的产出总目标：《中共中央关于国民经济和社会发展第十三个五年规划的建议》提出全国的GDP增长速度至少6.5%。

全国的减排总目标：《中华人民共和国国民经济和社会发展第十二个五年规划纲要》明确要实现“化学需氧量、二氧化硫排放分别减少8%因此，平均每年需要削减1.8%。

公平目标：未来时(第t+1期)期内，各省区人均碳排放量与全国总的人均碳排放量的最大偏离控制在现有范围内；其他非期望产出的公平目标不设置。各种要素投入分配和各种期望产出分配的公平目标均不设置。

4.5 实证过程及结果

通过LINGO软件实现DEA模型的效率评价和资源分配，具体的计算过程与结果分析如下:

第三步，求解模型(4)，从而获得实现管理者期望目标下的各省碳排放的分配结果(见表5)，将该分配结果与各省实际碳排放额相减，则获得各省碳减排任务。

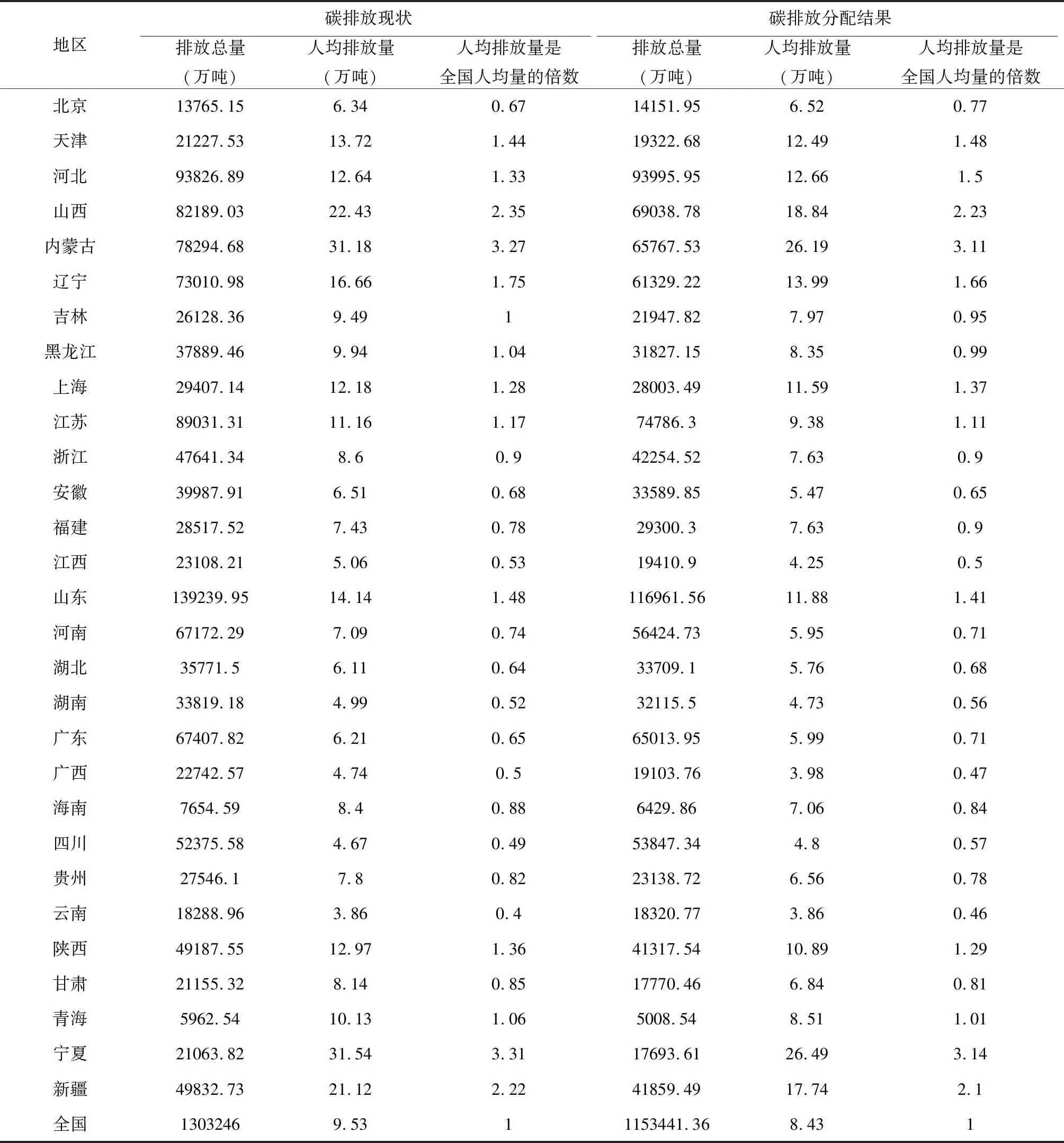
表5 各省碳排放现状与分配结果的比较

根据表5的比较分析可以得知，本研究的分配方案中，全国碳排放总额为1153441.36万吨，比当前碳排放总量缩减了8%，同时，各省人均排放分配量与全国人均量的倍数控制在(0.45，3.02)范围内，比当前的(0.40，3.31)有所缩小，即，人均碳排放分配量与全国总的人均分配量的偏离有所缩小，更加公平了。

5 结语

本研究构建的基于未来效率的资源分配DEA模型具有以下的几个特色：

首先，该DEA模型是基于未来效率对未来时期的资源进行分配。该模型根据以往的投入产出数据，预测未来时期的效率，从而实现未来时期的资源的最优分配。

其次，该DEA模型是在潜力评估的基础上设定目标，从而使资源的分配方案更具可行性。该DEA模型分三阶段在评估各DMU的要素投入的最大缩减潜力、非期望产出的最大缩减潜力期望产出的最大增长潜力的基础上，根据管理需要选择一个合理的目标。

第三，该DEA模型具有多目标决策的特点。管理者不仅可以改变九个硬性目标的参数值以及调整三个软性目标的优先顺序，而且还可以在每个步骤相应软性目标最大实现潜力评估的基础上，在相应目标的最大实现潜力范围内进一步设定一个期望的合理软性目标，从而形成各种目标导向的资源分配方案。这样，更适合于管理者运用该分配模型进行分配方案设计。

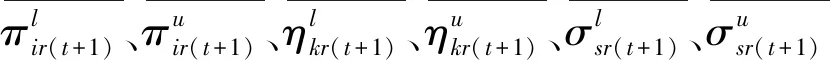
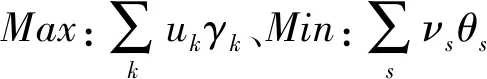
实证分析中，运用本研究构建的DEA方法灵活有效地解决了我国各省碳减排潜力评估及责任分配问题，一方面，在评估各省区经济增长、节能、减排等方面潜力的基础上，实现了全国碳排放总额比当前碳排放总量缩减了8%，另一方面，人均碳排放分配额与合理的人均分配量的偏离有所缩小，从而实现了兼顾公平与效率的碳排放额的分配。