基于光场一阶关联的时域成像*

张瑞雪 李洪国 李宗国

(天津理工大学理学院,天津 300384)

1 引 言

鬼成像,又称关联成像,是一种基于光的涨落关联获得物体图像的新型成像技术.具有涨落关联性质的光源发出的光被分束器分成两路,在一条光路(物光路)中,透过物体的光被一个不具有空间分辨的桶探测器接收,在另一条光路(参考光路)中光经过一段自由传播后直接被一个具有空间分辨的探测器接收,其中单个探测器都不能够得到物体的像,但是对两个探测器接收到的信号进行关联测量却可重建物体的图像信息[1].国内外关于鬼成像的研究逐步走向应用,从最初的纠缠光源[2]到热光源[3-12]、空间光调制器或投影仪调制光源[13],从双臂鬼成像到单臂鬼成像、计算鬼成像[14,15],从室内近距离成像到室外远距离遥感成像应用[16-18]、从光子鬼成像到电子鬼成像[19].另外在鬼成像的应用方面还有关于鬼成像质量影响因素的相关研究,如大气湍流对成像的影响[20,21]、高阶关联鬼成像的可见度及信噪比[22,23]、多波长光源对信噪比的影响[24]、基于光学参量放大的鬼成像[25]、压缩感知鬼成像[26,27]、计算鬼成像质量的优化[28]等.最近,Cao等[29]研究了基于热光源的分数阶鬼成像,Yang等[30]首次从概率密度角度理论解释了热光的鬼成像,并进行了实验验证.利用空域中光的近轴衍射和时域中脉冲信号在色散介质中色散之间的空间-时间二象性,很多空域系统的时域对应因此得到了快速发展,比如超快光信号处理[31]、超快示波器[32,33]、时域隐身[34]等.

最近,Ryczkowski等[35]实现了基于二阶关联的时域鬼成像[36-38],为利用关联方法进行时域信号的探测开辟了新方向.此前Gao等[39]基于物理上描述鬼成像的强度关联(二阶场关联)函数可以分解为一阶场关联,提出并实现了基于热光场一阶关联的空域关联成像.而目前关于一阶关联的时域成像还没有相关研究,本文基于空间-时间二象性,设计并研究基于热光场一阶关联的时域成像,促进利用光场关联实现时域信号探测的应用.这种成像模式采用 Mach-Zehnder干涉仪通过物光场和参考光场的关联获得物体的图像信息,装置类似于基于一阶场关联的全息成像[39],但区别在于一阶关联全息成像中是记录物体的干涉条纹,然后通过再现获得物体的图像.另外这种成像模式与基于一阶场关联的光学相干层析(OCT)成像的相同点是都利用了低相干光源的时间相干性,但区别在于OCT成像装置是基于迈克耳孙干涉仪[40].本文第2部分给出实现一阶关联时域成像的装置图并进行理论分析研究,第3部分给出基于一阶关联实现时域物体成像的结果,并分析光源的脉冲宽度和相干时间对成像可见度和分辨率的影响,最后进行总结.

2 理论分析

2.1 时域脉冲响应函数

为了便于后面得到描述一阶时域成像的关联函数,首先分析给出时域脉冲响应函数.在空域中,描述近轴光场衍射的波方程为

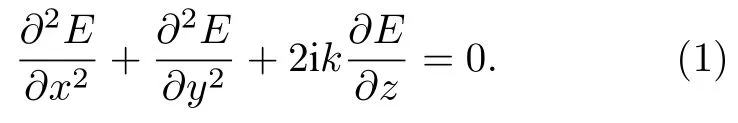
该波方程的通解形式上可写为

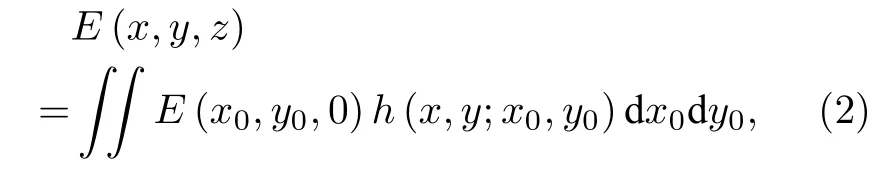
其中E(x0,y0,0)和E(x,y,z)分别表示位置(x,y,z)和初始位置 (x0,y0,0)处的光场,h(x,y;x0,y0)是描述光学系统的脉冲响应函数,其表达式为

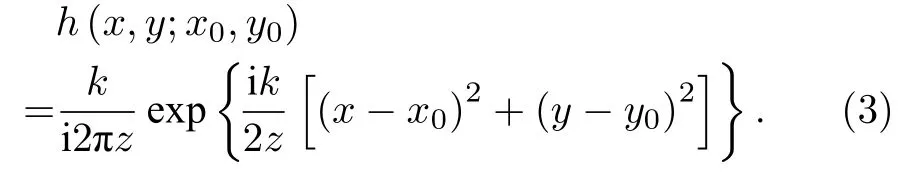
上面的解也可以通过菲涅耳衍射理论得到.这表明近轴波方程与菲涅耳衍射理论存在内在联系.相应地,在一阶色散近似条件下[41],描述窄带光脉冲在色散介质中色散的微分方程为

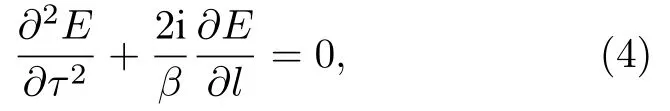
其中E表示与在色散介质中传播的时间τ和距离l有关的光场分布,β是光在色散介质中的群速度色散系数.根据以上方程,描述脉冲色散的微分方程与描述近轴光波空间衍射的波方程形式相同.因此时域脉冲在色散介质中的色散可看作空域中光波近轴衍射的时间对应,即空间-时间二象性.(4)式的解与近轴衍射波方程解的数学形式相似,可写为

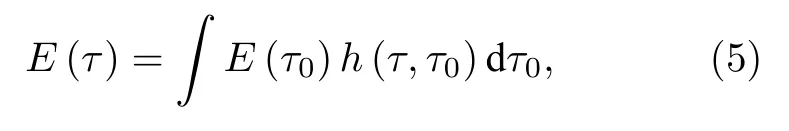
其中脉冲响应函数h(τ,τ0)表征在色散介质中系统在τ时刻对初始时刻τ0输入脉冲的响应,其形式为[41]

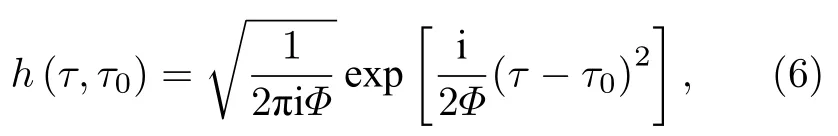
其中Φ=βl表示长度为l的色散介质的群延迟色散参量.基于上述二像性,也可写出其他光学系统的脉冲响应函数.因此类比空域物体的脉冲响应函数,时域物体的脉冲响应函数为

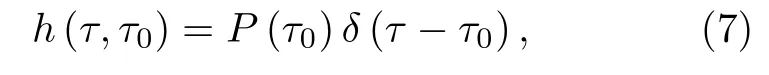
其中P(τ)是描述物体时序结构的函数,可以通过电光调制器调制产生.同理,时域透镜的脉冲响应函数可写为

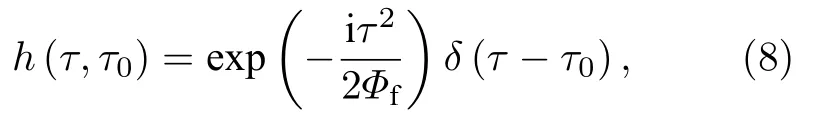
其中Φf表征时域透镜的“焦时间”,类似于空间透镜的焦距.时域透镜用于对光脉冲施以二次相位调制,该调制也可通过电光调制器实现.

2.2 一阶关联时域成像理论分析

采用类似于空域中借助 Mach-Zehnder干涉仪实现一阶关联成像的思想,本文设计的一阶关联时域成像装置示意图如图1所示.具有光场涨落关联性质的时序光源 TS 发出的光在色散介质如光纤中传播一段距离后被光纤分束器 FBS1分为强度相等的两束光,一束光(物光束,Path1 )在色散介质中传播,依次经过时域物体 TO 和时域透镜 TL1后到达光纤分束器 FBS2；另一束光(参考光束,Path2 )在色散介质中经过时域透镜 TL2后也到达光纤分束器 FBS2,两束光在光纤分束器 FBS2中汇合后被探测器 Detector 接收,探测器采集得到的信号通过数据采集卡将信号数据存储至计算机.

图1 基于光场一阶关联的时域成像装置示意图Fig.1.Schematic illustration for first-order temporal imaging.

根据(6)式—(8)式,并考虑脉冲响应函数的级联性质,可得物光路 Path1 和参考光路 Path2 系统的脉冲响应函数分别为：

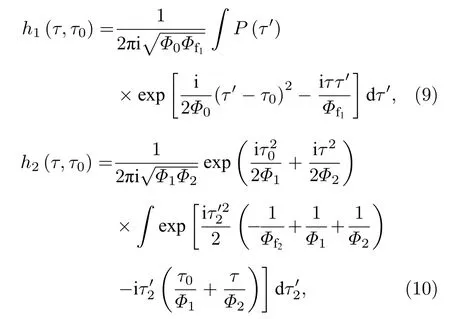
其中Φ0表示光源与时域物体之间色散介质的群延迟色散参量,Φf1和Φf2分别表征时域透镜 TL1和TL2的“焦时间”,时域透镜 TL1与时域物体 TO,时域透镜 TL1与光纤分束器 FBS2之间色散介质的群延迟色散参量也均等于Φf1,时域透镜 TL2与光源 TS,时域透镜 TL2与光纤分束器 FBS2之间色散介质的群延迟色散参量分别为Φ1和Φ2.为了便于讨论,假设时序热光源是时域非相干光的,其关联性质满足

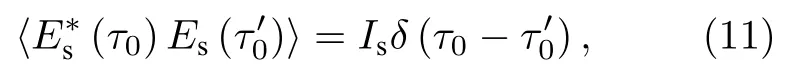
其中E表示与在色散介质中传播的时间τ和距离l有关的光场分布,β是光在色散介质中的群速度色散系数.根据以上方程,描述脉冲色散的微分方程与描述近轴光波空间衍射的波方程形式相同.因此时域脉冲在色散介质中的色散可看作空域中光波近轴衍射的时间对应,即空间-时间二象性.(4)式的解与近轴衍射波方程解的数学形式相似,可写为

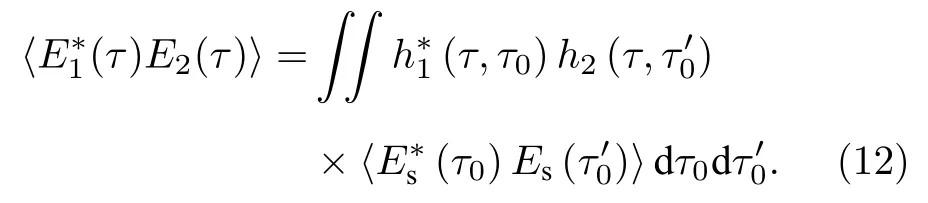
将(9)式—(11)式代入(12)式,探测面处的一阶场关联可进一步写为

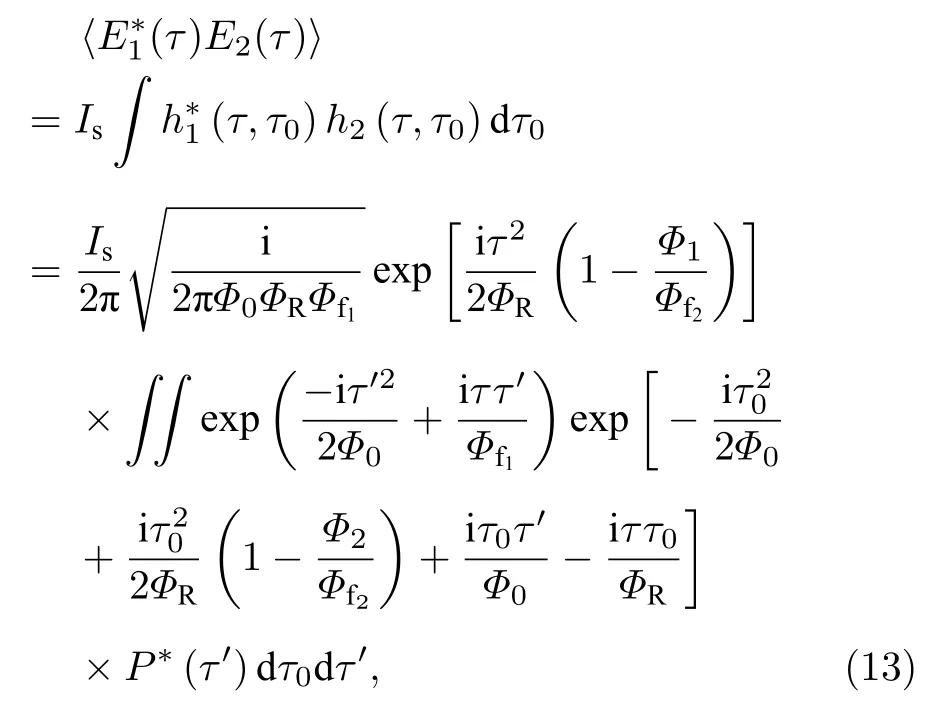
其中ΦR=Φ1+Φ2-Φ1Φ2/Φf2.当成像条件满足时,上式化简为

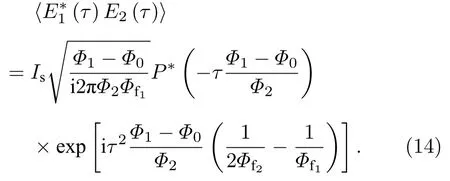
(14)式表明时域物体的像会受到二次相位因子的影响.分析可知,当各部分色散介质的群延迟色散参量之间关系满足Φ1-Φ0=Φ2=Φf1=2Φf2时,二次相位因子项可以被消掉,这样(14)式最后化简为

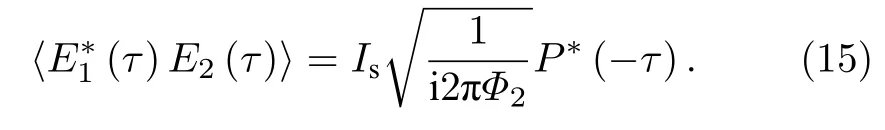
由此可知,通过一阶场关联可再现时域物体信号的像,即可以实现时域成像,不需要额外的色散补偿或消除.

3 成像质量分析

前面讨论了利用时序非相干热光源实现一阶关联时域成像,考虑到实际光源发出的脉冲宽度和相干时间是有限的,因此利用更为普遍的热光源模型即高斯-谢尔模型,分析成像可见度和分辨率.高斯-谢尔型时序光源的一阶场关联满足

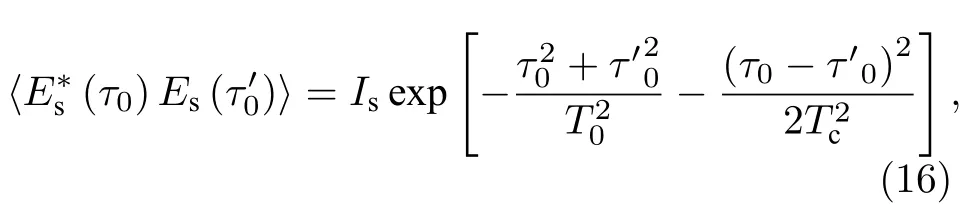
其中T0和Tc分别表示光源发出脉冲的宽度和相干时间.探测面处的强度是物光路和参考光路的光场叠加的模方,即

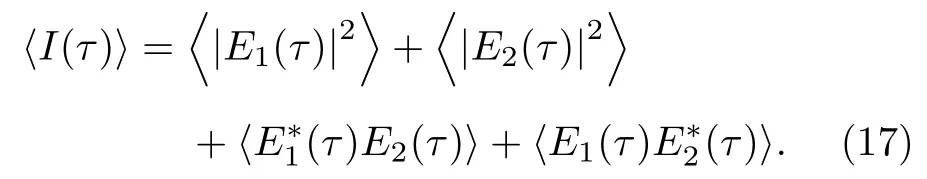
将(5)式、(9)式、(10)式、(12)式和(16)式代入(17)式,假设时域物体距离光源很近,即Φ0=0,并考虑成像条件和消去二次相位因子条件可得探测面处一阶关联时域成像的强度表达式为

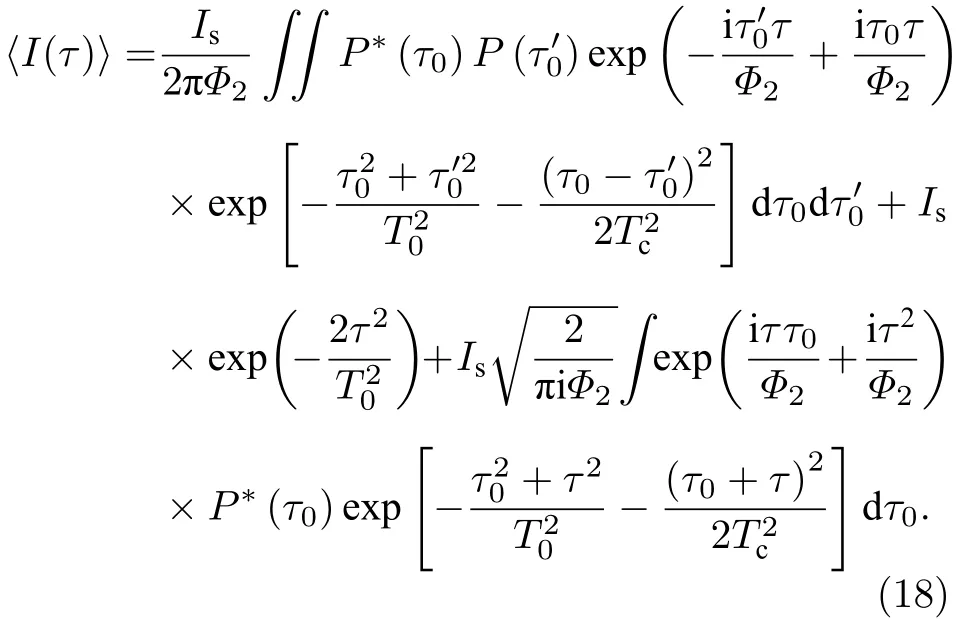
假设时域物体为具有一定间隔的两个矩形波信号,矩形波间隔和宽度分别为20和8 ps,选取色散介质的群延迟色散参量为Φ0=0,Φ1=Φ2=Φf1=2Φf2=50ps2.首先分析保持光源脉冲相干时间不变,改变光源脉冲宽度的成像结果.根据(18)式,模拟得到了光源脉冲相干时间为Tc= 0.5 ps,脉冲宽度T0分别为5,10,50和100 ps条件下的成像结果,如图2所示.根据时域物体成像质量的可见度,图3给出了光源相干时间Tc= 0.5 ps 条件下,成像可见度随光源脉冲宽度的变化曲线.由图2可以看出,随着脉冲宽度的增加,时域物体的图像可见度逐渐降低但分辨率逐渐变好,即时域物体的矩形波逐渐显现.由图3可以看出,在保持光源脉冲相干时间不变时,随光源脉冲宽度的增加,成像可见度逐渐减小,这与空间域二阶鬼成像的结果类似[42].这是因为当光源脉冲宽度大于时域物体信号持续时间时,场关联才能完整展现物体的信息.

此外,Qu等[43]的研究结果表明,在二阶时域鬼成像中时域物体图像的保真度(表示像与原物体信号的相似度)随脉冲宽度的增加而增加.图2和图3表明随着脉冲宽度的增加,一阶时域成像也有类似的结果,即图像与原物体信号的相似度逐渐增加.一阶时域成像的优点在于成像质量除了与光源的脉冲宽度和相干时间两个参量有关以外,还与物光和参考光的强度比有关,相同条件下成像可见度比二阶时域鬼成像的高[39].但是一阶时域成像对物光信号不执行桶探测,需要响应较快的探测器,而二阶时域鬼成像在这方面具有优势,因为二阶时域鬼成像对物光执行桶探测只需慢响应探测器即可.

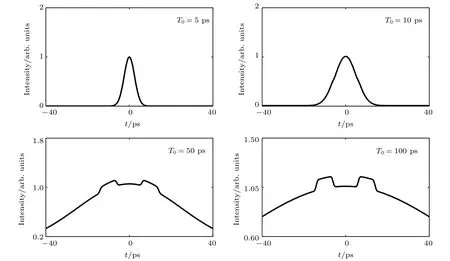
图2 光源相干时间为0.5 ps,光源脉冲宽度宽度分别为5,10,50和100 ps条件下的关联像Fig.2.The correlated images with different pulse widths of the source 5,10,50 and 100 ps,for the source’s coherence time 0.5 ps.

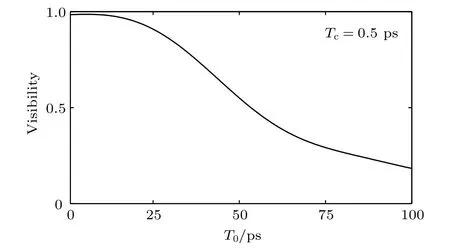
图3 光源相干时间Tc为0.5 ps时,成像可见度随光源脉冲宽度的变化曲线Fig.3.The imaging visibility as a function of the source’s pulse width for the source’s coherence time 0.5 ps.

最后分析当保持光源脉冲宽度不变,改变光源相干时间的成像结果.根据(18)式,模拟得到了光源脉冲宽度为T0= 100 ps,光源相干时间Tc分别为0.5,1.5,5和10 ps条件下的成像结果,如图4所示.由图4可以看出,随着相干时间的增加,时域物体的像逐渐失真,即成像的分辨率(物体像的半高宽)逐渐变差.由图5可以看出,随着光源相干时间的增加,成像可见度逐渐增加最终基本保持不变.光源的相干时间类似于空域鬼成像中光源的横向关联长度(散斑尺寸),光源的相干时间越短,成像系统对于时域物体的时序结构细节分辨能力越好,但可见度越差.这就说明基于一阶关联的时域成像中,可见度和分辨率二者有相互矛盾的关系.因此需要适当选取光源的脉冲宽度和相干时间以获得兼顾可见度和分辨率的理想成像结果.由以上分析可知,当光源的相干时间为0.5 ps、脉冲宽度为T0= 100 ps 时,间隔为20 ps、宽度为8 ps的时域矩形波型物体的成像质量(兼顾可见度和分辨率)较好.

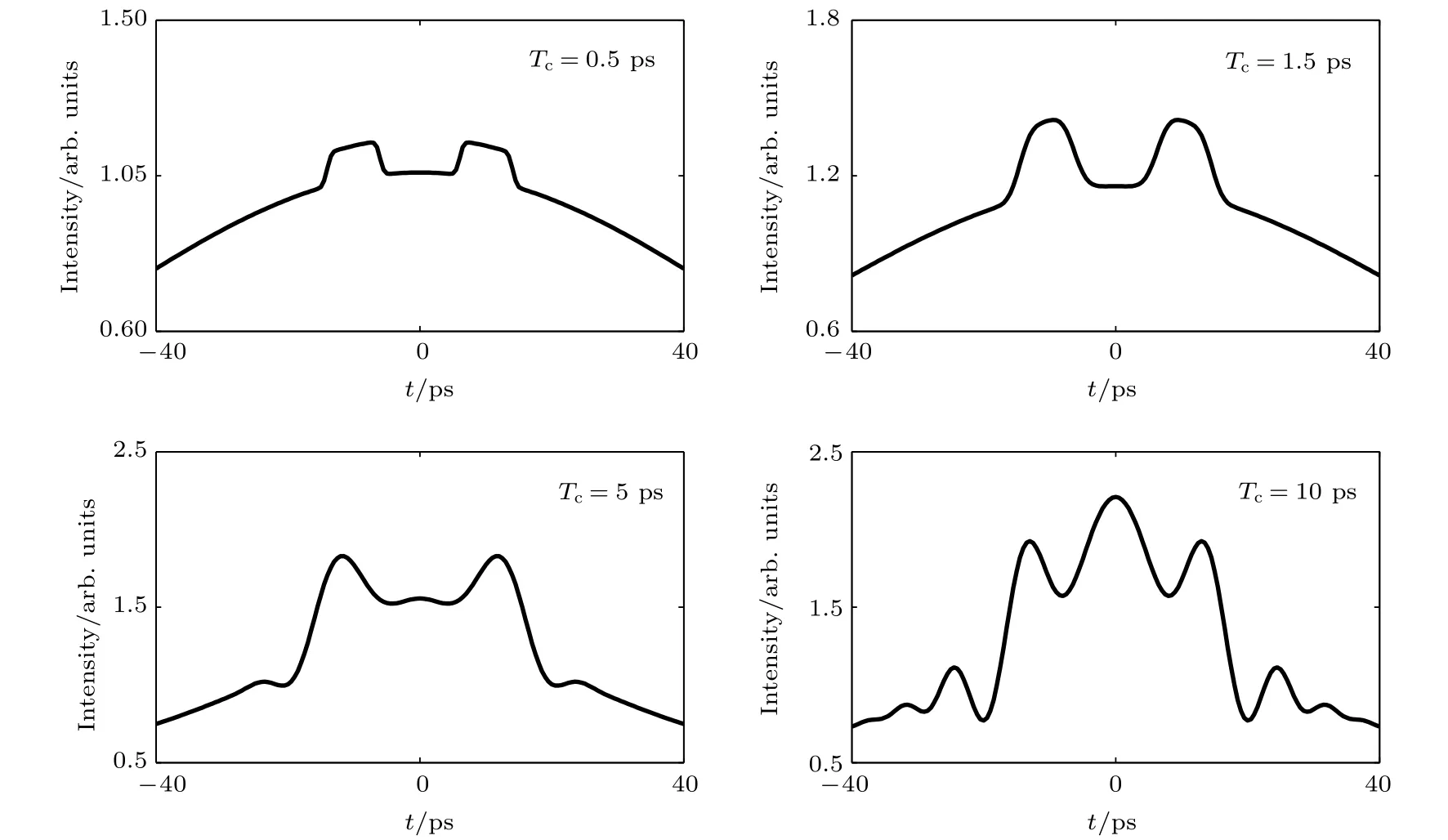
图4 光源脉冲宽度为T0= 100 ps,光源相干时间Tc分别为0.5,1.5,5和10 ps条件下的关联像Fig.4.The correlated images with different source’s coherence time 0.5,1.5,5 and 10 ps,for the source’s pulse width 100 ps.

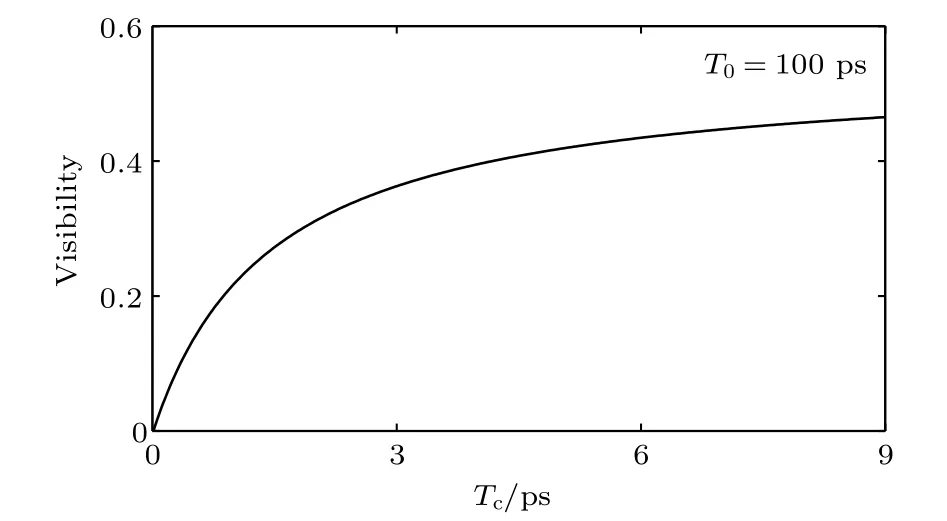
图5 光源脉冲宽度为100 ps时,成像可见度随光源相干时间的变化曲线Fig.5.The imaging visibility as a function of the source coherence time for the source’s pulse width 100 ps.

4 结 论

本文根据空间光束近轴衍射和光脉冲在色散介质中色散现象之间的空间-时间二象性,在时域脉冲响应函数基础上,研究了基于一阶场关联的时域成像,并以高斯-谢尔型热光源为例,模拟再现了时域物体信号的成像结果,分析了光源脉冲宽度和相干时间对成像可见度和分辨率的影响.结果表明,利用一阶场关联在不需要色散补偿或消除的条件下可以实现时域物体信号的成像,并且随着光源脉冲宽度的增加,像的可见度逐渐增加,而随着光源脉冲相干时间的增加,成像分辨率逐渐变差,但是可见度逐渐增加.该结果对于场关联在时域信号测量中的应用具有促进作用.