Multi-disciplinary design optimization with variable complexity modeling for a stratosphere airship

Shi YIN ,Ming ZHU ,Hoqun LIANG

a School of Aeronautic Science and Engineering,Beihang University,Beijing 100083,China

b School of Automation Science and Electrical Engineering,Beihang University,Beijing 100083,China

KEYWORDS Multi-disciplinary design optimization;Sensitivity analysis;Stratosphere airship;Surrogate model;Variable complexity modeling

Abstract This paper proposes a hybrid architecture based on Multi-disciplinary Design Optimization(MDO)with the Variable Complexity Modeling(VCM)method,to solve the problem of general design optimization for a stratosphere airship.Firstly,MDO based on the Concurrent SubSpace Optimization(CSSO)strategy is improved for handling the subsystem coupling problem in stratosphere airship design which contains aerodynamics,structure,and energy.Secondly,the VCM method based on the surrogate model is presented for reducing the computational complexity in high-fidelity modeling without loss of accuracy.Moreover,the global-to-local optimization strategy is added to the architecture to enhance the process.Finally,the result gives a prominent stratosphere airship general solution that validates the feasibility and efficiency of the optimization architecture.Besides,a sensitivity analysis is conducted to outline the critical impact upon stratosphere airship design.

1.Introduction

A stratosphere airship is a young aircraft with limited design experience but has been the much-researched topic during recent decades,which is qualified for long endurance missions with large payload operating at a high altitude.New technologies in low-resistance shape,high-strength fabric,renewable energy,and flight control for loiter capability make a stratosphere airship more realizable.1Nowadays,a stratosphere airship sows its origins from earth observation, maritime monitoring, missile warning, communication signal relays,etc.,namely,it is mooted as an affordable part substitute for a near-earth orbit satellite or can eliminate the need for multiple aircraft sorties to sustain continuous on-station keeping.2

The ambient environment where a stratosphere airship works is much more rigorous than that of conventional aviation,which has an altitude of approximately 10-55 km,low temperature to-60°C,thin air with a low density(about 1/13 of that at the sea level),low pressure(about 1/18 of that at the sea level),severe ozone corrosion,and intense ultraviolet.Fortunately,the stratosphere emerges very little convection,and its resultant turbulence occurs there.1,3Hence,with a sizable super-pressure hull and low cruise velocity,a stratosphere airship fits the environment better than a conventional aircraft.

Nomenclature

ΔPaero(Pa) Differential pressure causing by aerodynamics

ΔP(Pa) Differential pressure

ΔPhydr(Pa) Differential pressure because of a small hydrostatic effect referring to the lifting gas and the air outside the hull

ΔPint(Pa) Differential pressure to avoid caving the nose of the airship

ΔPwork(Pa) Differential pressure required to maintain the hull rigidity

ηcbrEfficiency decay caused by curvature of the hull shape

ηmpptEfficiency of the maximum power point tracker

ηpropPropulsive efficiency

ηscEfficiency of solar array power generation

ηwthrWeather factor

ρair(kg/m3) Air density

ρfabric(kg/m2) Areal density of the hull material

ρHe(kg/m3) Helium density

σv(MPa) Maximum von Mises stress

ε1Empirical factor for the optimization constraint

ε2Empirical factor for the optimization constraint

a1(m) Forward major radius of the hull ellipse

a2(m) Backward major radius of the hull ellipse

Ahull(m2) Area of the hull surface

Asc(m2) Area of a solar cell

B(N) Buoyancy of the airship

b(m) Minor radius of the hull ellipse

CDVDrag coefficient based on the volume

D(N) Aerodynamic drag of the airship

d/l Slenderness ratio

DP(N) Pressure drag

Dν(N) Viscous drag

Eday-density(J/m2) Daily energy per square meter

Eelec(J) Energy collection by the solar array

g(m/s2) Acceleration of gravity

Imax(W/m2) Maximum solar irradiance strength

l(m) Length of the hull

m(kg) Total mass of the airship

marray(kg) Mass of the solar array

mfixed(kg) Fixed mass

mHe(kg) Mass of helium

mhull(kg) Mass of the hull

mpld(kg) Mass of the payload

mprop(kg) Mass of propulsion

msc(kg) Mass of a solar cell

mstru(kg) Mass of the structure

n Number of solar cells

p0(Pa) Ambient pressure

Ppld(W) Payload power

Pprop(W) Propulsion power

ptotal(Pa) Internal total pressure of the hull

Qreq(W) Requirement of energy

Qsup(W) Supply of energy

T(N) Thrust of airship propulsion

t0(K) Ambient temperature

tcruise(h) Total cruise duration

tday(h) Day cruise duration

u(m) Radial displacement on the maximum diameter of the hull

u(tail)(m) Displacement on the tail position of the hull

v(m/s) Airspeed

Vhull(m3) Hull volume

The typical state-of-arts in a stratosphere airship/balloon project/experiment are as follows:

Project Loon is now a research and development project being developed by X Company(formerly Google X)with the mission of providing Internet access to rural and remote areas.The project uses high-altitude balloons(see Figs.1 and 2)placed in the stratosphere at an altitude of about 18 km to create an aerial wireless network.4,5On October 9,2017,multiple balloons were spotted near Puerto Rico.On November 9,2017,Google had launched several balloons from Nevada and positioned them over Puerto Rico as part of an effort to bring 100000 people online.6

Fig.1 Google Loon project unit.

Fig.2 Stratosphere balloon.

The Lockheed Martin High Altitude Airship(HAA)(see Fig.3)and its sub-scale demonstrator,the High Altitude Long Endurance-Demonstrator(HALE-D)(see Fig.4),are an untethered,unmanned lighter-than-air vehicle that will operate above the jet stream in a geostationary position to deliver persistent station keeping as a surveillance platform,telecommunications relay, or a weather observer.7The HAA also provides warfighters affordable, ever-present intelligence,surveillance,reconnaissance,and rapid communications connectivity over the entire battle space.The technology is available now and ready for integration and flight test.Lockheed Martin and the U.S. Army launched the first-of-its-kind HALE-D on July 27,2011,demonstrating key technologies critical to the development of unmanned airships.The project demonstrated a variety of advanced technologies,including launch and control of an airship,communication links,unique propulsion system,solar array electricity generation,remote piloting communications and control capability,and in-flight operations.8

As a stratosphere airship has few referential design cases and successful experiments,this paper conducts the design process according to‘Yuan meng'stratosphere airship 2015 in Xilinhot,Inner Mongolia and‘Tian heng'stratosphere airship 2017 in Korla,Xinjiang,both of which were conducted by Beihang University,as are illustrated in Figs.5 and 6,respectively.9-11

The typical state-of-arts in stratosphere airship/balloon design optimization are as follows:

Fig.5 ‘Yuan meng'stratosphere airship non-forming launch.

Fig.6 ‘Tian heng'stratosphere airship virtual cruise.

A past study of Wang and Shan12on stratosphere airship design has carried out a shape optimization,but the study was limited to a single aerodynamics disciplinary.Ram and Pant13have suggested a multidisciplinary shape optimization of an aerostat envelope,and they maximized a single-object payload capability with constraints factors like the drag,volume,stress,and weight.Ceruti et al.14have proposed a multidisciplinary design of an unconventional airship with several heuristic algorithms,and the objective was the airship mass restricted to geometric parameters,speed,stability,etc.Wang et al.15have presented an analytical multidisciplinary optimization method to obtain a feasible stratosphere airship shape,but the method decoupled disciplines including aerodynamics,structures,energy,and weight.Liang et al.16have carried out a detailed conceptual design optimization for a highaltitude airship,and introduced an irradiance model for the energy subsystem,but other subsystems needed high accuracy due to the limit of analytical modeling.Yang and Liu17have proposed a conceptual design of a stratosphere airship focusing on energy balance based on multidisciplinary analysis,especially,a detailed curved paving model and an output power model for the solar array were built and verified with a maneuverable wind resistance strategy,but the optimization was limited to a single-objective mass and lack of a structural constraint.Yang18have studied on a thermal and trajectory model of a stratosphere airship during the ascent phase,and figured out the influences of the initial volume ratio of helium gas and film radiation on the ascent thermal behavior.Yang and Liu19have suggested a renewable power system model extending the endurance of a stratosphere airship,and the operation considered ways such as the wind resistance strategy,the photoelectric transformation efficiency of the solar array,and the specific energy of the lithium battery.

In the problem of general design optimization for a stratosphere airship, the subsystem coupling problem originates from thrust-drag balance, buoyancy-weight balance, and energy-consumption balance operations through day and night,which associate aerodynamics-propulsion1,structureweight/payload20,and energy-consumption subsystems comprehensively21. Consequently, the MDO method aims to improve the virtual design proportion in the entire process,considering coupling of various disciplines and balances.To obtain the system optima,the MDO method devotes to establishing an overall framework using an efficient optimization strategy and collaboratively distributed computing networks.22Besides,the VCM method contributes to alleviating the significant computational expenses occurred in the high-fidelity Computational Computer-Aided Design(CAD)model,the Computational Fluid Dynamics(CFD)model,the Finite Element Analysis(FEA)model,and the energy program during the optimization loop.9

The remaining paper is organized as follows:Section 2 formulates the mathematical description of stratosphere airship design optimization and a task scenario;then in Section 3,we build the architecture of MDO with VCM;Section 4 gives the result of optimization and compares with a baseline,and conducts sensitivity analysis too;finally,Section 5 concludes the paper and discusses the future research direction.

2.Formulation of stratosphere airship design optimization

2.1.Design scenario

As a critical part of a stratosphere airship,the hull affects aerodynamic and structural performances besides energy supply.The shape of the hull is one of the essential elements in the design of a stratosphere airship,and hence the hull shape optimization is a key aspect of the research in this paper.The hull is the central part to produce lift and offer structural support,and it affects aerodynamic performance,strength,and stiffness of the airship significantly;consequently,fluid-structure interaction should be taken into consideration.Besides,we mainly lay the solar array of the energy system on the roof surface of the hull;thus,this area affects available power directly,which will have an impact upon the structure in turn,as is illustrated in Fig.7.10,23

According to‘Yuan meng'and‘Tian heng'stratosphere airships,the goals are set as in Table 1,while other system constants are listed in Table 2.10,24

Fig.7 General design flow.

Table 1 Design indices.

Table 2 System constants.

2.2.Mathematical description

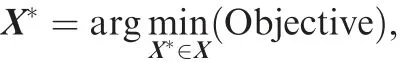
Fig.8 Improved NPL(National Physical Laboratory of UK)airship shape.

Table 3 System inputs.

Table 4 System outputs.

3.Architecture of MDO with VCM

In the MDO framework,we utilize CSSO based on the Kriging surrogate model to associate system and subsystem processes,as shown in Fig.9.16This strategy can decouple subsystem optimization temporarily and run parallel operations respectively while system optimization executes,but it still keeps coupled information in system and subsystem analysis.In other words,similar to system analysis,nonlocal state variables of each subsystem are derived from the Kriging surrogate model.26,27The Kriging surrogate model bridges each subsystem and gives a decent approximation on both continuous and discrete models.

For the optimization loop,if the framework runs on all the high-fidelity subsystem models,the computational complexity and cost would increase exponentially,and even unexpected high complexity and cost caused by the inherent coupled problem among subsystems.Therefore,to balance the computational cost and precision, we mainly utilize low-cost approximate analysis tuned by high-cost accurate analysis during iteration,which is called VCM.Specifically,the VCM method takes advantage of refined and computationally expensive models,which contain a CAD model,a CFD model,an FEA model,and an energy program in each subsystem analysis respectively,together with a rational and computationally inexpensive model,which is a surrogate model that mimics the features of an actual model by learning the inputs-to-outputs relationship with an acceptable precision.9

In system optimization,the strategy global to local can locate optima faster and more precisely, with the Multi-Island Genetic Algorithm (MIGA) for global search and NonLinear Programming by Quadratic Lagrangian(NLPQL)for local search.28While operating on the computationally inexpensive model,the VCM method calls computationally expensive models periodically for automatic error modification.What's more,with the purpose of accelerating convergence, adaptive sampling is used to generate Design of Experiment(DOE)samples.This sampling initiates with 30 initial points for the Kriging surrogate model which is updated with optimal data points continuously,where the optimal variables of surrogate-based optimization are sent to the highfidelity CFD model,FEA model,and energy program to recalculate,as is shown in Fig.10.Thus,the VCM method can run an efficient mechanism in computational complexity reduction without loss of accuracy.

Fig.9 CSSO based on surrogate model.

Fig.10 System optimization framework.

3.1.Hull geometric modeling

To seek potentially feasible geometric parameters in optimization,we decouple the geometric constraint between forward and backward major radii of the hull ellipse from the original NPL stratosphere airship envelope shape in Fig.11,and form an improved NPL stratosphere airship envelope shape in Fig.8.

The improved NPL stratosphere airship envelope shape is built by a parametric modeling method based on the secondary development of CATIA,and we use Visual Basic for Applications(VBA)script to drive the process and make the model ready for next phases,as is shown in Fig.12.

Fig.11 Original NPL airship shape.

Fig.12 Parametric modeling.

3.2.Aerodynamics subsystem

This subsystem aims at calculating the aerodynamic drag,outsurface pressure field,and propulsion energy requirement during level flight.

(1)In the CFD phase,considering fidelity and computational cost, the model mesh size is controlled to 860,000 by ICEM.To fit the operation environment of the stratosphere airship,we choose the k—ω(2 eqn)-SST turbulence model in FLUENT.We use Tcl script to drive ICEM and FLUENT in the optimization framework based on their secondary development.

(2)Considering the efficiency of propulsion,the power conquering drag to maintain level flight is as follows:

The factor propulsive efficiency ηpropis listed in Table 5.

Table 5 Energy subsystem factors.

3.3.Structure subsystem

This subsystem conducts a structural analysis of the stratosphere airship hull to acquire stress and displacement distributions.

In the FEA phase,considering fidelity and computational cost,the model element size is controlled to 17,102.To fit the operation environment of the stratosphere airship,we choose the explicit dynamic solver in ABAQUS. We use Python script to drive modeling and analysis based on the secondary development of ABAQUS.

The external pressure field,derived from the output of the out-surface pressure field in the CFD phase,is interpolated by the ABAQUS data cloud input module.Additionally,the internal total pressure consists of four parts,16which are the differential pressure to avoid caving the nose of the airship Δpint,the differential pressure caused by aerodynamics Δpaerowith maximum Cp=0.33 occurred at the position of the maximum diameter,the differential pressure because of a small hydrostatic effect referring to the lifting gas and the air outside the hull Δphydr,and the differential pressure required to maintain the hull rigidity Δpwork.Finally,the differential pressure Δp defines the workload in FEA.The helium density ρHeis estimated in Eq.(12).

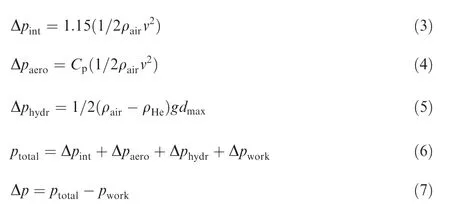
3.4.Energy subsystem

This subsystem models the solar irradiance and estimates the energy balance.As is illustrated in Fig.13,the schema includes a solar array,energy storage batteries,and an energy manager,which operates power generation and energy consumption.

(1)Irradiance model

Solar irradiance depends on various factors such as geographic position,time,solar panels orientation,and albedo.In our case,a model from Ref. 29 which is the total(beam and diffuse)solar radiation on a horizontal surface versus time during a clear and mostly cloudy day,at latitude 43N°,near equinox,is simplified for flat surfaces by the positive part of a sinusoid30as shown in Figs.14 and 15.The daily energy per square meter is calculated as in Eq.(8).Taking into account the possibility of cloudy days,a constant ηwthris added with a value between 1(clear sky)and 0(mostly cloudy sky).

Fig.13 Schema of power transfer.

Fig.14 Total solar radiation on horizontal surface.

Fig.15 Approximation of irradiance with sinusoid.

(2)Energy balance for sustainable flight

The energy balance depicts that the energy subsystem maintains the energy supply for propulsion power conquering aerodynamic drag and payload consumption during a day and night,as is illustrated in Eq.(1).

Solar energy collection by the solar array on the roof of the stratosphere airship hull depends on lots of factors,for example,the area of a solar cell Asc,the efficiency of solar array power generation ηsc,the efficiency decay caused by curvature of the hull shape ηcbr,and the efficiency of the maximum power point tracker ηmppt,which are listed in Table 5.The energy supply and requirement are defined below:

3.5.System mass estimation

(1)Fixed mass

In this stratosphere airship design optimization,the mass of propulsion,avionics,and energy storage batteries is assumed fixed as

Table 6 Comparison between optima and baseline.

Fig.16 System parameter change rates.

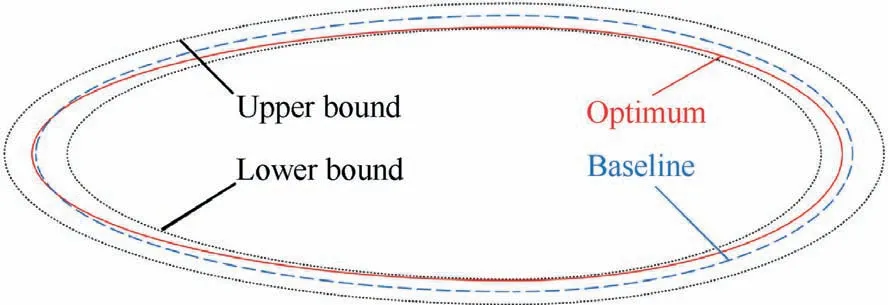
Fig.17 Change in the optimization of the hull shape.

Fig.18 Performance parameter change rates.

Table 7 Performance parameters change rates.

(2)Structural mass

During a level fight,the hull is in the state of overpressure fulfilled with helium.The mass of helium can be estimated as follows:

Due to the additional material in manufacture,the mass of the hull can multiply a factor of 1.2 as

Thus,the mass of structure in this stratosphere airship design optimization is

(3)Solar array mass

The mass of the solar array depends on the number and mass of solar cells as

Finally,the total system mass estimation is

4.Results and analysis

The framework is implemented on iSight 5.7 integrated with CATIA R21,ICEM 14.0,FLUENT 14.0,ABAQUS 6.13,and MATLAB 2013A.

The DOE work ran over a 2.4 GHz Intel Xeon E5-26650 with 64 G RAM workstation with windows 7 taking over 3 h 52 min 29 s.The optimization work ran over a 3.6 GHz Intel Core i7 with 16 G RAM PC with windows 7 taking over 7 h 35 min 49 s,which met the convergence criteria of error±E-3 during 23 iterations.

Fig.19 Velocity along Y axis contour around hull tail.

4.1.Comparison with baseline

In this paper,we compare the optima with the baseline of the stratosphere airship and illustrate the changes after optimization in Table 6 and Fig.16.The framework gives excellent results,for example,an 8.316%decrease in the total weight of the airship,a 14.825%decrease in the aerodynamic drag of the hull,a 7.5%decrease in the maximum von Mises stress of the hull,and a 14.571%decrease in the radial displacement on the maximum diameter of the hull.

Fig.20 Vorticity along X axis(wx)contour around hull.

Fig.21 Optimized maximum von Mises stress contour and total displacement contour under payload.

Fig.17 shows an intuitive comparison among the optimum,baseline,and bounds of the outline of the stratosphere airship hull.The solid red line is the optimum,the long dash blue line is the baseline,and the dot black lines are for bounds.Accordingly,slenderness ratio diminishment with 7.354%is a leading trend of the process,which helps to alleviate the pressure drag with 21.707%mainly induced by the maximum windward cross-section,and the trend diminishes the viscous drag of the hull with 9.649% due to the surface area decreasing 9.792%,as is shown in Fig.18 and Table 7.Moreover,the trend lengthens the tail of the hull so that the curvature of the tail increases,followed by alleviation of flow separation due to a decrease of the adverse pressure gradient attached to the tail surface,as is illustrated in Fig.19.In Fig.20,compared with the baseline design,the optimized hull obtains a lower range and intensity of vorticity near and along the tail,which verifies the lower flow separation,and leads to a reduction in the total drag,too.Besides,slenderness ratio diminishment alleviates the maximum von Mises stress of the hull with 7.5%mainly induced by the minimum curvature of the hull shape,namely the maximum-diameter part,where the trend also improves the stiffness on this part with a 14.57%decrease of the displacement.As the relative shrink in the hull head,the curvature of the head shape increases so that a smaller stress and displacement will be obtained,which contributes to the global stiffness with a 3%displacement decrease along the horizontal axis,as illustrated in Fig.18 and Table 7.The stress and displacement contours of the optimized hull are illustrated in Fig.21,respectively.As for the energy subsystem,because we have a relatively wider experimental margin,the number of solar cells decreases with dramatic 38.89%as is in Table 6 and Fig.17;besides,its mass decreases accordingly,which gives a tremendous comprehensive improvement.

As is shown in Fig.22,due to the reduction of the surface area of the hull,the hull mass proportion decreases from 60.51%to 59.85%,which accounts for the bulk of the total mass.While the volume of the hull decreases after optimization,the helium mass decreases as well as the proportion changes from 7.96%to 7.28%.Because of the dramatic drop in the solar cell number,the energy subsystem mass decreases from 155.53 kg to 138.1 kg with a proportion from 12.4%to 12%correspondingly.As the mass quantities of payload and propulsion remain the same,the proportions in the total mass change following other aspects.

4.2.Sensitivity analysis

In the design optimization of a stratosphere airship,it is necessary to execute global sensitivity analysis by considering the uncertainty of multivariate inputs and quantify the impact upon multivariate outputs correspondingly.

In this situation,to improve the performance of stratosphere airship design optimization under an uncertain circumstance, we propose a global sensitivity analysis based on multidimensional spatial distance.31Because distance metrics can be used to describe the difference among samples of multivariate outputs responses in multivariate data,the multidimensional spatial distance method can fit in characterizing the uncertainty of this process with multivariate outputs.

Fig.22 Mass distribution of baseline and optima.

To multidimensional spatial sample (X,Y), d2(Y,E(Y))indicates the distance of Yjin the output response Y=[Y1,Y2,...,Yj,...,Ym] deviating from the mean value E(Y),as is in Eq.(17).Specifically,in Eq.(18),the conditional mean value E(Y|Xi)can be calculated when element xiof input Xkin Eq.(20)is fixed as the k-th DOE sample.Furthermore,the impact upon system uncertainty induced by the uncertainty of each input is described by the deviation of multivariate outputs from their mean values in term of spatial distance,namely,global sensitivity S.As a result,substituting Eq.(17)into Eq.(18),we get Eq.(19),in which the global sensitivity Siof element xiis the ratio of the summation of the variance of each output's conditional mean value to the summation of the variance of each output.

In practice,due to the enormous difference in the dimensionality of each output response,a direct addition of variance may extinguish contributions of some outputs with relatively little dimensionality,and thus global sensitivity will suffer significant information loss.As a solution,we nondimensionalize the outputs in Eq.(21).

Table 8 Global sensitivity results of system.

From data sets corresponding to 4 inputs each of which has 30 sample points generated by DOE,we can figure out a rank of the system global sensitivity of each input b ＞a2＞a1＞n as well as the impact upon system uncertainty caused by the uncertainty of inputs,as is illustrated in Table 8 and Fig.23.Moreover,the interaction sensitivity index is nonnegligible,namely,a significant proportion of uncertainty brought about by inputs is caused by the interaction between inputs as well as all the higher-order terms in sensitivity indices,which also reveals the coupling effect among system variables.

Fig.23 Global sensitivity analysis of system.

Fig.24 Global sensitivity analysis of each output.

Additionally,to investigate the impact caused by the uncertainty of inputs upon σv,we treat it as an output temporarily in this phase.In term of outputs sensitivity analysis,D,m,σv,and u get the ranks that are in accordance with b ＞a1＞a2＞n,b ＞a2＞n ＞a1,b ＞a2＞a1＞n,and b ＞a2＞a1＞n,as is shown in Table 9 and Fig.24.Generally,representing the maximum diameter and the maximum cross-section area of the hull shape,b dominates the aerodynamic pressure drag,the maximum stress,and the maximum displacement on the hull envelope.As a result,the sensitivity index of b comes first on each output.Likewise,a2has a larger impact than that of a1on each output most of the time,and n has a relatively larger impact on the mass of the hull.From the results,the bigger the global sensitivity of an input is,the more attention should be paid to it,and we should give prior control to these inputs.Last but not least,the interaction between inputs plays an important role in sensitivity analysis on each output,so a comprehensive consideration should also be given to smoothing the stratosphere airship design optimization.

5.Conclusions

This paper propose a useful stratosphere airship optimization and design architecture based on MDO with VCM, and employs it to find an optimized solution of stratosphere airship design under limited-experience condition.In the architecture,the CSSO strategy is used to improve MDO to handle the subsystem coupling problem which contains aerodynamics,structure,and energy.Moreover,the VCM method based on the surrogate model is used to reduce computational complexity during optimization with acceptable accuracy,and a globalto-local optimization strategy is added to enhance the process.As a result,compared with the baseline,the optima obtain a prominent improvement in the aerodynamic drag,structural weight,hull stress,displacement,etc.What's more,global sensitivity analysis is conducted to locate the impact of uncertainty brought about by inputs upon outputs,which helps a designer make clear the priority of input variables.

Table 9 Global sensitivity results of each output.

For the future research of stratosphere airship design optimization,the followings should be clarified.Firstly,the platform of the airship hull can be diversified and not just limited to NPL series.Secondly,other subsystems can be analyzed simultaneously,for example,route planning control for a specific mission or solar radiation adaptive tracking.Thirdly,new strategies and algorithms can be added to the optimization architecture to get a more accurate and efficient solution.

Acknowledgement

This work was supported in part by the National Key R&D Program of China(No.2016YFB1200100).