Multiphysics simulation method of Lamb wave propagation with piezoelectric transducers under load condition

Lei QIU,Xixi YAN,Xiaodong LIN,Shenfang YUAN

Research Center of Structural Health Monitoring and Prognosis,State Key Lab of Mechanics and Control of Mechanical Structures,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China

KEYWORDS Acoustoelastic effect;Lamb wave;Multiphysics simulation;Piezoelectric coefficient;Structural health monitoring;Time-varying condition

Abstract Lamb Wave(LW)simulation under time-varying conditions is an effective and low cost way to study the problem of the low reliability of the structural health monitoring methods based on the LW and Piezoelectric Transducer(PT).In this paper,a multiphysics simulation method of the LW propagation with the PTs under load condition is proposed.With this method,two key mechanisms of the load influence on the LW propagation are considered and coupled with each other.The first mechanism is the acoustoelastic effect which is the main reason of the LW velocity change.The second key mechanism is the load influence on piezoelectric materials,which results in a change of the amplitude.Based on the computational platform of the COMSOL Multiphysics,a multiphysics simulation model of the LW propagation with the PTs under load condition is established.The simulation model includes two physical phenomena.The first one is called solid mechanics,which is used to simulate the acoustoelastic effect being combined with the hyperelastic material properties of the structure in which the LW propagates.The second one is called electromechanical coupling,which considers the simulation of the piezoelectric effect of the PTs for the LW excitation and sensing.To simulate the load influence on piezoelectric materials,a non-linear numerical model of the relationship between the load and the piezoelectric coefficient d31 is established based on an experiment of the load influence on the LW.The simulation results under uniaxial tensile load condition are obtained and are compared with the data obtained from the experiment.It shows that the variations of the phase velocity and amplitude of the LW obtained from the simulation model match the experimental results well.

1.Introduction

In recent decades,Structural Health Monitoring(SHM)technology has gradually developed from theoretic and fundamental research to aerospace engineering applications with a very slow progress.1-3The time-varying problem is one of the main obstacles.4-8Real aircraft structures serve under uncertain time-varying conditions such as the environmental condition,the load condition,and the structural boundary condition.For example,the environmental condition includes temperature,humidity and noises,while the load condition includes normal flight load,overload and landing.Almost all the damage monitoring features of the SHM sensor signals can be directly affected by the time-varying conditions,which leads to the low reliability of damage monitoring.

Among SHM methods,Lamb Wave(LW)and Piezoelectric Transducer(PT)based method is a promising one because it has large monitoring area and is sensitive to small damage.9-15The basic principle of the method is to place a lot of PTs(eg.piezoelectric ceramics)on a monitored structure directly and obtain LW signals by the excitation and sensing of these PTs on line.Through the analysis of the LW features changed by damage,the damage can be evaluated.However,time-vary conditions can also introduce a large number of variations to the LW features so as to reduce the reliability of damage monitoring.To reduce the influence of time-varying conditions,several damage monitoring methods16-25such as the state compensation method,the baseline free method,the data normalization method,the pattern recognition method,and the probability statistic method have been proposed.Nevertheless,these methods have their own limitations for practical applications.

For aerospace applications,the above-mentioned damage monitoring methods together with some new methods still need to be further studied and validated.To achieve this point,the LW signals or data obtained from different states of aircraft structures under time-varying conditions are essential and necessary.For example,the LW signals under different temperatures or load conditions are needed to establish a reference database for the state compensation method,16,17and the LW signals at the health state and different damage states are needed to train the classifiers of the pattern recognition methods.22Furthermore,the probability statistic method has been considered to be a more feasible way to solve the timevarying problem but the LW signals obtained at the different states of aircraft structures under time-varying conditions are urgently needed to study the performance of the probability modeling and the migration feature of the corresponding probability model.23-25However,the time-varying conditions are often complicated and the corresponding experiments which are performed to obtain the LW signals are of highly cost and time consuming, especially to those experiments performed on real aircraft structures under real in-service conditions.To deal with this issue,the LW simulation under timevarying conditions is an effective and low cost way because the LW propagation in a real aircraft structure under timevarying conditions can be studied based on simulated data,and the simulated LW signals can also be used for the purpose of validating the relevant damage monitoring methods.

The LW simulation methods26-40based on Finite Element Analysis(FEA)has been widely studied in recent decades to achieve the simulation of the linear and non-linear LW propagation in isotropic structures,anisotropic structures and even complex structures.The method to simulate damage such as the crack of aluminum structures and the delamination of composite plates by FEA has also been proposed.28-30,34,38Furthermore,some of the simulations do not take the PTs into account while some of the simulations consider the full LW excitation-propagation-sensing by integrating the PTs with the FEA models.26There are two branches of the LW simulations which consider the PTs.The first branch uses the FEA to simulate the LW propagated in a structure and uses the piezoelectric constitutive equations in theory to calculate the LW excitation stress and the voltage of the LW sensing signals.The other branch directly integrates the FEA model of the PTs with the LW simulation by using the electromechanical coupling between the PTs and the structure.The latter branch is called multiphysics simulation.One physics is the electromechanical coupling governed by the piezoelectric constitutive equations to simulate the piezoelectric effect of the LW excitation and sensing.The other one is the solid mechanics governed by the wave motion equations to simulate LW propagation in a solid structure.The multiphysics simulation is closer to the actual situation and has been validated by comparing the simulated results with the experimental results.In addition,compared with the theory modeling and numerical analysis of the LW,41-43the LW simulation based on the FEA is more intuitive and easier to be applied to the complex structures.Furthermore,the spectral element method32and quadrature element method44which are based on higher order polynomials have also been studied to reduce the computational amount and improve the accuracy of the LW simulation.

Although the research on the FEA based LW simulation has been widely studied and validated as mentioned above,the FEA based LW simulation method under time-varying conditions is still rarely reported,especially for a simulation method which fully considers the influence of time-varying conditions obtained by the PTs adhered on a structure.

Among a lot of time-varying factors,the varying load condition is a main factor.According to the previous studies performed in a full-scale aircraft fatigue test,45the structural load can introduce large variations to the velocity and amplitude of the LW signals obtained by the PTs.Chen and Wilcox,46Michaels et al.,47,48Mohabuth et al.49have performed theoretic studies,numerical analysis and experimental research of the load influence on the propagation velocity of the LW.It has been proved that the main reason of the variations of the LW phase and group velocity under load condition is the acoustoelastic effect due to the change of structural material properties under an external load.In addition,according to the research performed by Lonkar50and Roy et al.,17the amplitude changes of the LW signals are caused by the variations of the piezoelectric coefficients of the PTs under load condition.

To simulate the load influence on LW,Lonkar et al.50studied an LW simulation method,in which the strain distribution introduced by a uniaxial tensile load was calculated by the computational platform of ABAQUS first and then the result was used to calculate the acoustoelastic effect in theory and to calculate the load influence on piezoelectric coefficients by a numerical model so as to obtain the final LW signals.In this paper, a simple but efficient method of the multiphysics simulation of the LW propagation with the PTs under load condition is proposed.The simulation method is based on the FEA and the two key mechanisms mentioned above including the acoustoelastic effect and the load induced changes on piezoelectric coefficients.Based on the computational platform of the COMSOL Multiphysics,a FEA model of the LW propagation with the PTs under load condition is established and the two key mechanisms are coupled with each other in the FEA model.The LW signals under load condition can be obtained directly from running the simulation model.The simulation results are in accordance with the experimental results.

This paper is organized as follows.In Section 2,the two key mechanisms are discussed in detail.Then in Section 3,an experiment is performed to study the load influence on the LW.A numerical model of the load influence on the PT is established as well.After that,the multiphysics simulation method of the LW propagation with the PTs under load condition is proposed and given in detail in Section 4.Then the simulation results are obtained and compared with the experimental results in Section 5.Finally,the conclusion is made in Section 6.

2.Simulation mechanisms of load influence on LW

A schematic diagram of the LW propagation with the PTs under load condition is shown in Fig.1.Two PTs are placed on a surface of a plate-like structure by an adhesive.One is used as an LW actuator and the other one is used as an LW sensor.To obtain an LW signal,an excitation waveform in voltage is applied to the actuator.Due to the inverse piezoelectric effect of the actuator,the LW is excited and propagates in the plate.When the LW propagates to the LW sensor,the LW signal is obtained due to the direct piezoelectric effect.

The duration time from the LW excitation to the LW sensing is very short because the frequency of the LW is often high and the propagation time of the LW is also very short.Therefore,the external load whose frequency is often very low can be treated as a static load compared with the duration time of the LW excitation-propagation-sensing.In this situation,the piezoelectric coefficients will be changed and the acoustoelastic effect will appear in the structure because of the stress introduced by the static load.The two mechanisms are related to the variations of the amplitude and propagation velocity of the LW respectively.They are discussed in detail as follows.

2.1.Load influence on amplitude of LW

The piezoelectric constitutive equations in strain-charge form of a PT are given by Eq.(1):

where e is the strain vector of the PT.d refers to the piezoelectric coefficient matrix.E is the electric field vector.s is the elastic compliance matrix.σ is the stress vector.D is the electric displacement vector and ε is the dielectric constant matrix.

The PT whose material is PZT-5A piezoelectric ceramic is often applied to the LW excitation and sensing.Normally,the thin discs of PZT-5A is polarized along axis 3 as shown in Fig.1.Thus E1=E2=0,E3≠0,d31=d32.Based on this point,the excited strain and electric displacement vector of the PT can be given by Eqs.(2)and(3):

If the plate shown in Fig.1 is isotropic,then only the external uniaxial load exists,that is σ1≠0,σ2,σ3,σ4,σ5and σ6are all zero.However,if the plate-like structure is anisotropic,the more complex stress field should be taken into account.

As shown in Fig.1,an adhesive layer is used to place the PTs on the plate and transfers the shear force generated by the LW actuator to the plate.In this situation,the shear-lag effect should be considered.51Based on this point and the above piezoelectric constitutive equations,the voltage Voutof an LW signal output from the LW sensor can be simply written as Eq.(4):52

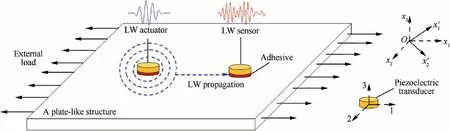
Fig.1 Schematic diagram of LW propagation with PTs under load condition.

where ν is the Poisson's ratio of PTs,C(Γ)is the function of shear-lag parameter Γ and are expressed as Eqs.(5),(6)and(7).

where the G and t are the shear modulus and thickness of the adhesive layer,respectively.The value of the parameter α depends on the LW modes.R is the radius of the PTs.I(ΓR)is the Bessel function.

The function C(Γ) represents the relationship between phase-shift of the LW propagation in the plate and the amplitude change of the LW related to the shear-lag model.However,according to the study of Roy et al.,17,52the change of the shear-lag parameter under load condition can be neglected.Therefore,according to Eq.(4),the amplitude of the output voltage of the LW sensor is related to the material properties of the PTs,namely,the piezoelectric coefficient d31,the dielectric constant ε33,and the elastic compliance s13.

According to the research performed by Lynch53and reclaimed by Roy et al.,17an unpolarized piezoceramic material usually has dipole moments in random orientations.However,after undergoing polarization,the dipole moments try to align themselves along the applied electric field direction for being constrained by the domain walls.Under the influence of applied mechanical loads,displacement of domain walls from its original configuration results in change in dipole moment and the net polarization.To further demonstrate this point,Fig.2(a)shows the electromechanical hysteresis loop of the piezoelectric material PZT-5A under no-load condition,which indicates the relationship between the applied electric field E3and the resulting total strain e33of the piezoelectric material.Based on experimental results of PZT-5A under different transverse compressive loads shown in Fig.2(b)-(d),the electromechanical hysteresis loops vary and the electric field effect gradually reduces accompanying the increment of the stress.The results show that the load can introduce polarization switching of piezoelectric materials so as to change the piezoelectric coefficients and dielectric constants.

However,the Lynch's research only used the transverse compressive load whose direction is the same with the polarized direction of the PZT-5A and only gives the variation of the piezoelectric coefficients d33and the dielectric constants ε33.As shown in Eq.(4),d31is a key parameter,whose variation under longitudinal compressive stress is quantitatively measured by Kang et al.54through a well-designed experiment.The ratio curves of piezoelectric coefficientof PZT-5A which present the ratio ofunder the longitudinal compressive stress σxxto theunder the stress-free state at different applied voltage xVppare given by Fig.3,which shows that the effect of external load on piezoelectric coefficient d31is non-linear consistent with the study of Crawley and Lazarus55Thus the output voltage of the LW sensor will be changed under the load condition.Importantly,according to their results,the elastic compliance s13and dielectric constant ε33of the PZT-5A almost do not change under the longitudinal stress while the influence of the load induced changes on the adhesive layer can be neglected.17In addition,though only the compressive load was used in the abovementioned research,the principle given above is also applicable under tensile load conditions.

In summary,the amplitude change of an LW signal is mainly caused by the variation of piezoelectric coefficient d31under external load condition.Therefore,in order to realize the simulation of the load induced influence on the LW,the numerical model of the variation of the d31under external load condition needs to be obtained first.

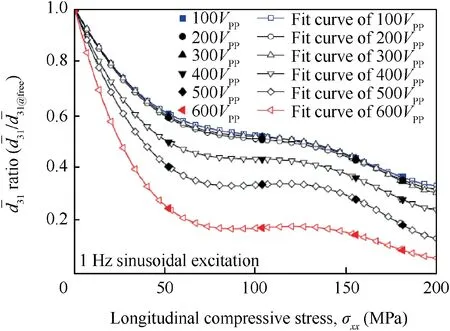
Fig.3 Piezoelectric coefficient d31 of PZT-5A under longitudinal compressive load.54.

Fig.2 Electromechanical hysteresis loops of PZT-5A under transverse compressive load conditions.53.

2.2.Load influence on propagation velocity of LW

The load influence on the propagation velocity of the LW can be explained by the acoustoelastic effect,which can describe the non-linear changes in the constitutive relation of the structures under external load condition.56The non-linear changes will induce the stress-dependence of the acoustic wave velocity in a solid media.In this situation,the linear elastic material of the solid media will become hyperelastic material due to the external load.This point is further explained as follows.

The wave equation of LW propagation on plate-like structure under static uniaxial stress can be expressed by Eq.(8):50

where u(xi,t)is the dynamic displacement in natural coordinates xi(i=1,2,3),σ0is the static stress,and ρ is the density of the plate.Γijklis the effective elastic modulus.It is expressed as Eq.(9),in which,u0represents the deformation caused by the stress,Cijklis the second order constants,andis the third order elastic constants as expressed by Eq.(10).

where δijis the second order unit tensor and Iijklis the fourth order unit tensor.

According to the Murnaghan theory,57the third order elastic constants for isotropic materials can be represented in terms of the Murnaghan constants l,m,and n as shown in Eq.(10).

Based on the above equations,when a plate-like structure is stress-free,the dispersion of the symmetric and antisymmetric modes of the LW propagation in the structure can be expressed as Eqs.(11)and(12):

where d is the half of the plate thickness.k=ω/c is the wavenumber,ω is the angel frequency of the LW,and c is the velocity of the LW.

The relative wavenumbers p and q of the LW are given by Eq.(13),in which,CLand CTare the propagation velocities of the longitudinal wave and transverse wave.They are expressed as Eqs.(14)and(15)respectively by the second order Lame constants λ and μ.

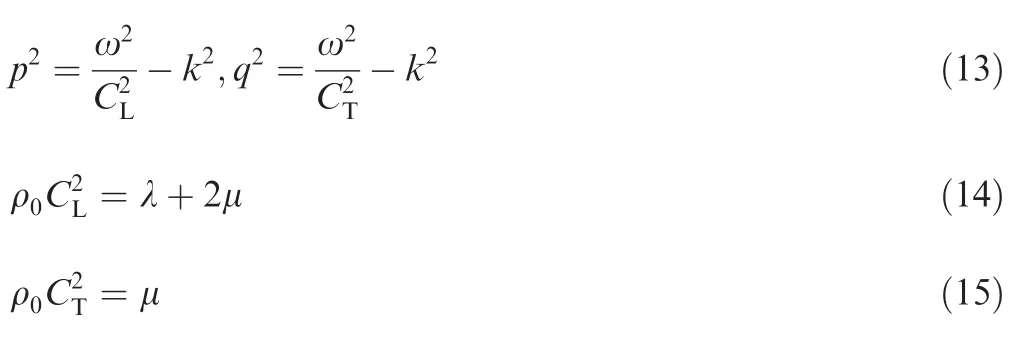
When the plate-like structure is under a stress condition because of an external uniaxial load,the above two velocities are obtained as Eqs.(16)and(17)respectively by combining with the third order Murnaghan constants l,m and n.In these two equations,T denotes the external load and K is the bulk modulus of the plate-like structure.

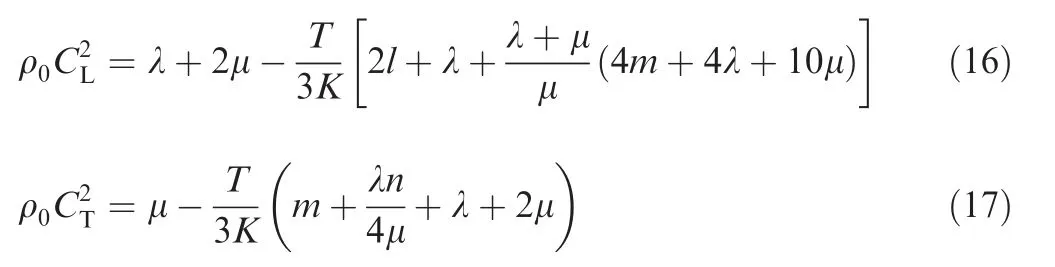
It can be known from Eqs.(16)and(17)that the two velocities become stress-dependent because of the external load due to the acoustoelastic effect,and the relationship between the velocity change and the stress is linear.Furthermore,the numerical dispersion curves under uniaxial tensile stress can be obtained based on Eqs.(16)and(17).They are shown in Fig.4 and a zoom-in view of the dispersion curves around 200 kHz is shown as well.It can be seen that the phase velocity Cpof the S0mode and A0mode of the LW will shift when the stress σ changes.Particularly,the dispersion curves at equally spaced stress are approximately equally spaced.Thus it is clear that if the load influence on the LW velocity change needs to be simulated,the acoustoelastic effect should be considered by combining with the third order elastic constants.Specifically,the third order Murnaghan constants l,m and n need to be integrated into the simulation model.

Fig.4 Numerical results of dispersion curves of LW under uniaxial tensile stresses.

3.Experiment of load influence on LW

3.1.Experimental setup and process

The experimental system is shown in Fig.5.The plate-like structure is an aluminum plate and its dimension is 400 mm×200 mm×2 mm(length×width×thickness).The material properties of the aluminum plate are:Young's modulus is 70 GPa,density is 2700 kg/m3and Poisson's ratio is 0.33.Three aluminum plates are used in the experiment and they are numbered as T1,T2 and T3.For each aluminum plate,two PTs are placed on the aluminum plate which are numbered as PZT1 and PZT2 to construct an LW pitch-catch channel.The material of the PTs is PZT-5A.The diameter and thickness of the PTs are 8 mm and 0.48 mm respectively.The adhesive is Araldite®2015.PZT1 is used to excite the LW and PZT2 is used to be an LW sensor.The distance between PZT1 and PZT2 is 200 mm.A strain gauges is placed on the back of the aluminum plate where PZT2 is located and is connected with a strain indicator(DPM-911A).The aluminum plate is fixed on a static tensile machine(CSS-44100)which is used to apply a static uniaxial tensile load to the aluminum plate.An integrated LW based SHM system52is used to excite and acquire the LW signals.

The load levels of the static uniaxial tensile load are shown in Table 1.From 0 MPa to 100 MPa,there are 11 levels of the load,with a 10 MPa interval to be applied to the aluminum plate.The LW signals are obtained at each level when the corresponding load is stable.A five-cycle sine burst modulated by a Hanning window58is used as the LW excitation signal and the amplitude is±70 V.The central frequency of the LW excitation signal is swept from 50 kHz to 250 kHz with 10 kHz interval.The sampling rate is set to 10 MSamples/s.In order to reduce signal noise,the average sampling is adopted.The same experimental process described above is applied to the three aluminum plates(T1 to T3)one by one.The measuredstrain shown in Table 1 is the average strains measured from the three aluminum plates.

Table 1 Uniaxial tensile load condition of experiment.

3.2.Experimental results

Fig.6 shows the LW signals of central frequency 200 kHz obtained from the aluminum plate T1 at all load levels.These signals are de-noised by the method based on complex continuous Shannon wavelet transform.59The zoom-in views of the amplitude and phase variations of the S0mode are also given in Fig.6 for a better observation.It can be noted that the amplitude and the phase delay of LW signals are increasing accompanying the increment of the load.

Figs.7 and 8 show the variation trend of the amplitude and phase velocity of the S0mode and A0mode of the LW signals at central frequencies fcwhich is 150 kHz, 200 kHz, and 250 kHz,respectively.To measure the change of phase velocity,Eq.(18)is used.43The results indicate that the phase velocity of the two modes decreases linearly and the amplitude of the two modes increases non-linearly accompanying the increment of the load.

Fig.5 Experimental system of load influence on LW.

Fig.6 LW signals of central frequency 200 kHz at all load levels.

Fig.7 Phase velocity and amplitude variations of S0 mode under uniaxial tensile load condition.

Tables 2 and 3 give the quantitative variations of the amplitude and phase velocity of the LW signals at the three central frequencies respectively. The decreasing rate of the phase velocity under different central frequencies are also given.It can be known that the decreasing rate increases with the increment of central frequency.In addition,the decreasing rate of the phase velocity of the S0mode is larger than that of the A0mode,indicating that the phase velocity of the S0mode is more load-sensitive.The variation of the amplitude is measured by Eq.(19).The amplitude variations of the two modes of the LW signals at the three central frequencies under different load levels are averaged correspondingly.The average results of all load levels are fitted by a second order polynomial as given by Eq.(20).The fitting results are also shown in Tables 2 and 3.It can be noted that the main increasing rate p2of the amplitude of the S0mode is nearly the same with that of the A0mode because the amplitude change is caused by the change of piezoelectric coefficients under load condition.The change of piezoelectric coefficients is not related to any mode.

Fig.8 Phase velocity and amplitude variations of A0 mode under uniaxial tensile load condition.

Table 2 Quantitative variations of S0 mode under uniaxial tensile load condition.

Table 3 Quantitative variations of A0 mode under uniaxial tensile load condition.

where Cpis the phase velocity and lpis the LW propagation distance.Δt is the time shit of constant phase of the LW signal.Amplevelis amplitude of LW signal at the corresponding load level.σ is the load induced stress(Unit:MPa).

As mentioned in Section 2.1,the numerical model which can be used to describe the load influence on piezoelectric coefficient d31is needed for the LW simulation but it is difficult to be measured directly when the PTs have been placed on the structure.Actually speaking,the LW signal obtained from a simulation model should match the real LW signal.However,for the research on the time-varying problem,it is enough if the variation trend of the simulated LW features can match those of the real LW features.Considering that the load influence on the PTs is the main factor that changes the amplitude of the LW signals, the numerical model is established to be Eq.(21)based on the amplitude change obtained from the above experimental results.In this paper,only the S0mode of the LW is considered to be simulated.Thus p1and p2are-1.100×10-5and 0.0042 respectively.

4.Multiphysics simulation method

Based on the simulation mechanisms and experimental study,the multiphysics simulation method is proposed in this section.Firstly,the whole simulation model will be given.Then the three key parts of the simulation model including the materials,the simulation physics,and the simulation solver will be given and discussed in detail.

4.1.Simulation model

It can be known from Fig.1 that the two physics need to be coupled with each other to simulate the LW propagation with the PTs under load condition.One is the electromechanical coupling governed by the piezoelectric constitutive equations to simulate the LW excitation and sensing.The other one is the solid mechanics governed by the wave motion equations to simulate the LW propagation in a solid structure.Furthermore,the variation of the LW phase velocity can be simulated by the acoustoelastic effect due to that the material properties of the structure are non-linear under load condition and the variation of the LW amplitude can be simulated by integrating the numerical model given by Eq.(21)into the piezoelectric constitutive equations of the PTs.

Therefore,to simulate the LW propagation with the PTs under load condition,the simulation model needs to meet the following requirements.(A)The electromechanical coupling and solid mechanics should be coupled with each other in the simulation model.(B)The acoustoelastic effect,the piezoelectric effect,and the load influence on the PTs should be integrated into the simulation model.(C)The simple and complex geometry of aircraft structures can both be supported.(D)Voltage excitation signal can be input to a PT and output voltage of the PTs can also be obtained.

In this paper,the computational platform of the COMSOL Multiphysics60is adopted because it meets the requirements listed above.Furthermore,the method in this paper concentrates on the simulation of the LW propagation with the PTs under load condition and only the two physics mentioned above are considered,while thermophysics,acoustic physics etc.are also needed to be coupled with the two physics to further simulate the LW propagation with the PTs under more comprehensive time-varying conditions.The COMSOL Multiphysics has the advantage of multiphysics coupling.Based on the COMSOL Multiphysics,the architecture of the multiphysics simulation method of the LW propagation with the PTs under load condition is proposed as shown in Fig.9.

In this paper,an aluminum plate with two PTs placed on the structure by an adhesive as shown in Fig.10 is adopted as a typical case to realize the LW simulation with the PTs under load condition.The simulation results can be compared with the experimental results given by Section 3.2.The load and boundary conditions are also shown in Fig.10.Though a plate-like structure is adopted in this paper,the models of complex geometry can also be simulated such as an aircraft

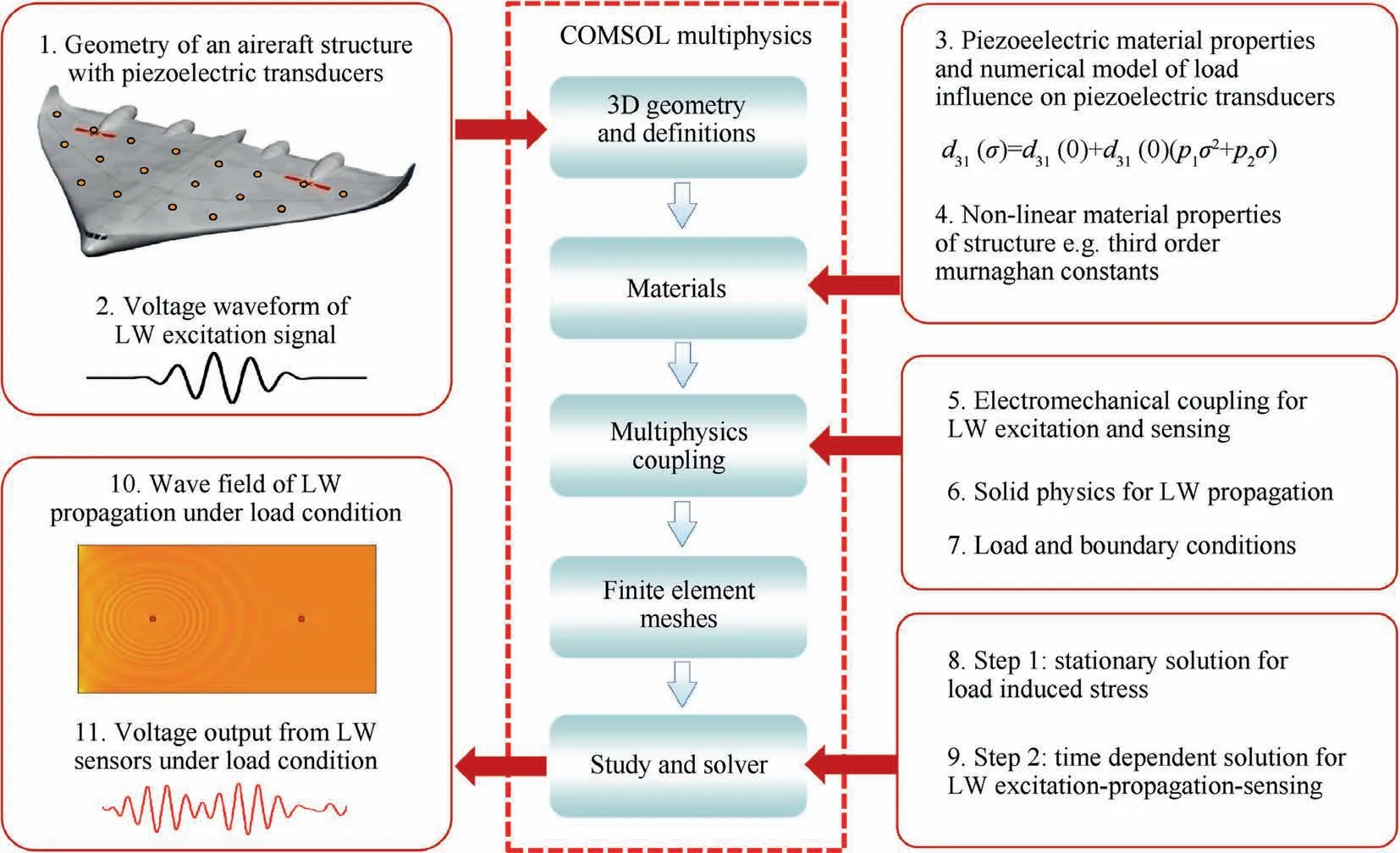
Fig.9 Architecture of multiphysics simulation method.

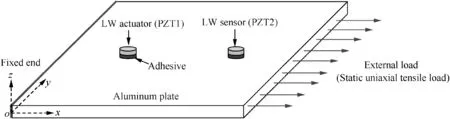
Fig.10 Load and boundary conditions of simulation case.

where A is the half voltage amplitude,f is the central frequency and N is the number of peaks.

(2)Materials

The Materials include the material properties of the PT,the adhesive layer,and the aluminum plate.They will be given in Section 4.2.

(3)Multiphysics coupling

The Multiphysics include the electromechanical coupling and the solid mechanics.They are coupled with each other and will be given in detail in Section 4.3.

(4)Finite Element(FE)meshes

The type of the finite element mesh adopted in this paper is Free Tetrahedral which is a polynomial interpolation function element of the second order with ten nodes.For LW simulation,the FE meshes of the PTs,the adhesive layers,and the aluminum plate need to be divided respectively.For the aluminum plate,the mesh size depends on the LW wavelength.For the LW of 200 kHz on the aluminum plate of thickness 2 mm,the phase velocities of the S0mode and A0mode are 5382 m/s and 1731 m/s respectively. Therefore, the wavelengths of the S0mode and A0mode are nearly 27 mm and 9 mm respectively.According to the research on the LW simulation,28the largest mesh length is recommended to be smaller than 1/6 of the wavelength.Though only the S0mode is considered in this paper,the wavelength of A0mode is used to be the reference to determine the mesh size.Thus the largest panel with stiffeners,wing spar,composite structures and other complex structures.

The simulation model is described as follows based on the modeling process shown in Fig.9.

(1)3D geometry and definitions

The geometry includes the 3D geometric model of the structure,the PTs and the adhesive layers.The dimension of the aluminum plate is 400 mm×250 mm×2 mm(length×width×thickness). For the PTs, the diameter is 8 mm and the thickness is 0.48 mm.The coordinates in x-y plane of the two PTs are(100,125)mm and(300,125)mm respectively.The distance between the two PTs is 200 mm.For adhesive layers,the diameter is 8 mm and thickness is 0.08 mm.

The definitions include two parts.The first part is the voltage excitation signal of the LW.For the comparison with the experimental results,the excitation signal of a five-cycle sine burst modulated by a Hanning window is used which is expressed as Eq.(22).The corresponding parameters are set to A=35 V,f=200 kHz and N=5.The second part,the LW observation probe is connected with the upper surface of PZT2.The type of the probe is voltage.The average voltage of the whole surface will be output.mesh size and smallest mesh size of the aluminum plate are set to 1.5 mm and 1.0 mm respectively.The mesh size of the PTs and the adhesive layers are set to 1.0 mm and 0.5 mm respectively.

Due to the small size of the meshes,the complete meshes consists of nearly 790000 domain elements,240000 boundary elements and 2000 edge elements.There are nearly 3600000 degrees of freedom.Therefore,the computer work station HPZ840 with Windows 10 operating system and 512 GB RAM is used to run the simulation model.There are 2 CPU clusters in the work station and each of them contains 14 CPU cores.In addition,the work station has 56 computational threads totally.The actual computation time to render one simulation is around 5 hours.

(5)Study and solver

The Study and Solver will be given and discussed in detail in Section 4.4.

4.2.Simulation materials

The material of the aluminum plate is shown in Table 4 which contains the third order Murnaghan constants for the simulation of the acoustoelastic effect.The material of the PTs is shown in Table 5.It is PZT-5A and the piezoelectric coefficient d31is based on Eq.(21)for the simulation of the load influence on the PTs.The adhesive layer is Araldite®2015.The density,Poisson's ratio,and Young's modulus of the adhesive layer are 1400 kg/m3,0.33 and 1.85 GPa respectively.61

4.3.Simulation physics

The simulation physics is shown in Fig.11,which is consisted of the two physics modules of the COMSOL Multiphysics including the Solid Mechanics module and the Electrostatics module. The Solid Mechanics is used to simulate solid mechanics of the aluminum plate,the PTs and the adhesive layers.The Electrostatics is used to simulate the electrical feature of the PTs.Consequently,the electromechanical coupling of the PTs for the LW excitation and sensing is simulated by both the two physics modules.The LW propagation in the alu-minum plate is simulated by the Solid Mechanics module.The two physics are coupled by the Multiphysics-Piezoelectric Effect and are described as follows.

Table 4 Material properties of aluminum plate.

Table 5 Material properties of PTs(PZT-5A).

(1)In Solid Mechanics,the Fixed Constraint and Boundary Load are used to simulate the fixed end and the external uniaxial tensile of the aluminum plate as shown in Fig.10,respectively.The load is applied to the plate from 0 MPa to 100 MPa with a 20 MPa interval(Six load levels totally).The Hyperelastic Material is used to realize the simulation of the acoustoelastic effect.In the material model of the Hyperelastic Material,the Murnaghan model is adopted and the values of the third order Murnaghan constants given by Table 4 is used.The Piezoelectric Material combined with the Electrostatics is used to realize the simulation of the PTs.The Mechanical Damping in the Piezoelectric Material is adopted,in which,the Rayleigh damping is used and the parameters are set to α=0 and β=2.2×10-8.62The Low-Reflecting Boundary is used to reduce the LW boundary reflection.The damping type is set to be‘P and S waves'.

(2)In Electrostatics,the Ground is the electric ground of the PTs and is connected with the lower surface of the PTs.The Electric Potential 1 and Electric Potential 2 are a zero potential and the voltage excitation signal of the LW,respectively.They are connected with the upper surface of PZT1 but are mutually exclusive.This point will be explained in Section 4.4.

4.4.Simulation solver

To solve the multiphysics simulation model given above,two study steps are adopted to construct the Study of the simulation model,as shown in Fig.12.The first step is the Stationary used to calculate the load induced stress.After that,the Time Dependent is performed to simulate the process of the LW excitationpropagation-sensing with the PTs under the load condition.The results of Step 1 are used to be the initial values of Step 2.

For each step,the Physics and Variables Selection is also shown in Fig.12.In Step 1,the Electric Potential 1 of zero potential is enabled to disable the PZT1 but the Electric Potential 2 of the LW excitation is disabled.This is due to two reasons.Firstly,if the PZT1 is not disabled in Step 1,the load would introduce stress to PZT1 and make it generate a large DC bias voltage.In Step 2,the DC bias voltage would act as a step excitation to introduce a frequency wideband LW propagating in the aluminum plate so as to lead a false LW sensing signal output from PZT2.Secondly,Step 1 is a stationary study and there is no need to excite the LW.In Step 2,the Electric Potential 1 is disabled and the Electric Potential 2 is enabled for the LW excitation.

The solver runs once for each load level mentioned in Section 4.3.Thus the LW signals under all load levels can be obtained.The simulation time step and time range in Step 2 are set to 1×10-7s and from 0 s to 1×10-4s,respectively.

5.Simulation results

To validate the simulation method,the simulation results are given from the following three aspects,(A)the wave field of the simulated LW to observe that the LW should be correctly excited;(B)the simulated LW signals and group velocity should match the theoretic dispersion curve and the experimental results; and (C) the phase velocity and amplitude changes of the simulated LW signals under different load levels should match the experimental results.

Fig.11 Architecture of multiphysics simulation method.

Fig.12 Setup of simulation solver.

5.1.Wave field of simulated LW

Except for the six load levels mentioned above,the external load of 1 MPa is also applied to the aluminum plate to obtain a typical wave field of the LW propagation with the PTs under load condition.The typical wave fields at different time t are shown in Fig.13.It can be seen that the S0mode and A0mode of the LW are excited and propagate correctly under the load condition.The result indicates that the simulation solver is established and runs correctly.

5.2.Simulated LW signals and group velocity

Fig.13 Wave field of LW propagation with PTs under load condition(Load 1 MPa).

The simulation signal under the load of 0 MPa and the experimental signal under the load of 0 MPa are compared with each other as shown in Fig.14(a).In the simulation model,there is no charge amplifier but the experimental system has one.Thus for a better comparison,the two signals are processed by complex continuous Shannon wavelet transform and are normalized based on the amplitude of S0mode,as shown in Fig.14(b).It can be seen that the S0mode of the two signals match well,but there is a small error of the amplitude and phase of the A0mode.The error is mainly introduced by the large mesh size considering A0mode and the linear free tetrahedral element cannot guarantee enough accuracy to properly represent A0mode behavior.

Table 6 gives the comparison of the simulated LW group velocity with the theoretic group velocity and experimental group velocity.Compared with the theoretic group velocity,the relative errors of S0mode and A0mode of the simulated LW are 3.5%and 1.3%,respectively.Compared with the experimental group velocity,the relative errors of the two mode of the simulated LW are 0.2%and 0.7%,respectively.The results indicate that the simulation results match the theoretic dispersion curve and experimental results.

5.3.Simulated LW signals at all load levels

The simulated LW signals at all load levels are shown in Fig.15.The zoom-in views of the phase and amplitude variations of the S0mode are also given in Fig.15 for a better observation.It can be seen that the variation trend of the phase and amplitude of the simulated LW signals is in agreement with that of the experimental LW signals shown in Fig.6.

Figs.16 and 17 show the quantitative variations of the phase velocity and amplitude.They also show the comparison with the experimental results.It can be noted that the phase velocity decreases linearly and the amplitude increases nonlinearly accompanying increment of the load.The slope of phase velocity change is -0.467 m·s-1·MPa-1, which matches the experimental result,-0.440 m·s-1·MPa-1.The small error may be introduced by the material difference of the aluminum plate between the experiment and simulation model.Based on the numerical model given by Eq.(21),the simulation of the load influence on the PTs is realized so as to introduce the variation of the LW amplitude.The amplitude variation also matches the experimental results.

6.Conclusions

This paper proposes a simple but efficient method for the multiphysics simulation of the LW propagation with the PTs under load condition based on COMSOL Multiphysics.The acoustoelastic effect and the load influence on the PTs are integrated into one multiphysics simulation model.The simulation of the acoustoelastic effect is realized by using the hyperelastic material model which contains the third order Murnaghan constants.The simulation of the load influence on the PTs is realized by establishing a d31numerical model of stressdependence based on the experimental data.The simulation solver is established by combing the stationary analysis and time-dependent analysis together.The whole multiphysics simulation is fulfilled in one computational platform and in one simulation model.The simulation results under uniaxial tensile load from 0 MPa to 100 MPa are obtained and are compared with the experimental results.It shows that the results obtained from the simulation match the experimental results well which indicates the correctness of the proposed simulation method.

To perform the proposed simulation method,two key parts need to be known beforehand:

(1)The first part is the numerical model of the piezoelectric coefficient d31of stress-dependence.According to the simulation results, it is preliminarily concluded that numerical model established by a calibration experiment on a simple structure under load condition can be applied to more complex structures and load conditions.The reason is that the load influence on the PT is structure-independent and is only stress-dependent.50

Fig.14 Comparison of LW signals between simulation and experiment.

Table 6 Comparison of simulated LW group velocity with that of theory and experiment.

Fig.15 Simulated LW signals at all load levels.

Fig.16 Comparison for phase velocity variations of S0 mode between experiment and simulation.

(2)The third order elastic constants of the structure in which LW propagates needs to be measured especially for the LW simulation on composite structures.63

The future work is planned to be performed based on the following five branches:

(1)It can be seen that the numerical model of the varying piezoelectric coefficients under time-varying conditions is the key to realize the multiphysics simulation.Therefore,some well-designed experiments will be performed to measure the properties of the PTs under time-varying conditions.

Fig.17 Comparison for amplitude variations of S0 mode between experiment and simulation.

(2)The time to render one simulation is long.To further reduce the computational amount of the simulation method,the spectral element method30and even quadrature element method42will be studied and combined with the simulation method.

(3)The multiphysics simulation of the LW propagation with the PTs under temperature condition will be studied and will be combined with the method proposed by this paper to achieve a comprehensive multiphysics simulation of the LW propagation with the PTs under time-varying conditions.

(4)Some damage simulation methods will be studied and combined with the multiphysics simulation method.

(5)Composite structures have been widely applied to aircraft structures. Thus the multiphysics simulation method of the LW propagation in the composite structures under time-varying conditions will be studied.

Acknowledgements

This work is supported by the National Natural Science Foundation of China(Nos.51635008 and 51575263),the Fok Ying Tung Education Foundation of China(No.161048),the Program for Distinguished Talents of Six Domains in Jiangsu Province of China (No. GDZB-035), the Priority Academic Program Development of Jiangsu Higher Education Institutions of China.