基于X光机图像识别的双边滤波和同态滤波相融合技术∗

李 海 杨骁勇 凤四海

（中国民用航空飞行学院 广汉 618300）

1 引言

随着计算机图像处理技术的发展，图像处理的算法逐渐应用在机场安检、视频图像识别、危险特征提取等领域［1］。机场的旅客行李中含有大量的灰度噪声和伪信息，给开机员正确识别危险品带来了困难，因此需要进行X光机图像伪信息去除和轮廓域平滑处理［1］。目前常见的针对X光机图像增强的方法有灰度变换法，改变亮度法，边缘增强等方法。

在安检过程图像识别中，张宁等［1］提出了一种轮廓波域边缘检测的民航机场X光机图像识别的优化方法，提高了对危险品图像的识别能力；该方法的缺点是对于图像的采集过程精度要求较高。金华勇等［2］提出星卡测试法，即采用高吸收系数的下料制作星型，获得图像；该方法的缺陷在于两条中心轴之间的角度偏离导致测量误差比较大。陈善婷等［5］提出一种用双边滤波器对X射线图像进行平滑滤波的方法。

受到成像过程中受检物体材料的影响，安检过程中很多情况下图像的高频部分在短时间内很难辨认其边缘特征。本文在前期工作的基础之上，基于X光机的图像识别进行研究，提出一种双边滤波和同态滤波相融合的方法，仿真实验表明其方法对与X光机成像图像具有较好的处理效果。

2 双边滤波和同态滤波原理

双边滤波（bliateral filter）是一种可以保边去燥的滤波器，是空间滤波器和值域滤波器的自合［6］。空域滤波是对空间上临近点的加权平均，至于滤波是根据周围像素点与中心像素点的值差来加权平均，加权系数均随着距离的增加而减少。

2.1 双边滤波

2.1.1 空域滤波卷积

设 f(x)为输入图像；h(x)为输出图像，则

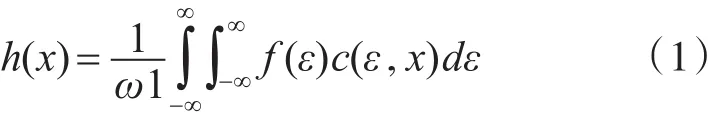
其中c(ε，x)度量领域中心点x与邻近点ε的几何邻近度，ω1为归一化参数。

2.1.2 值域滤波卷积

设 f(x)为输入图像；h(x)为输出图像:

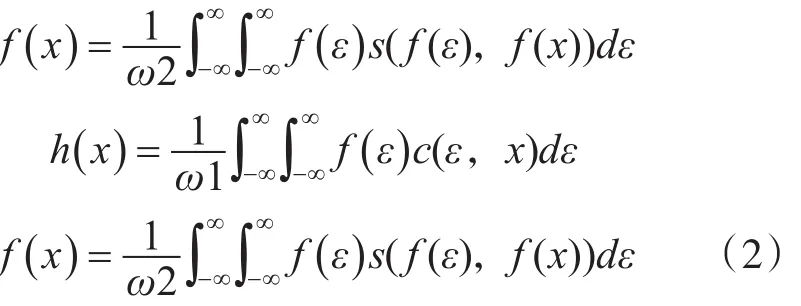
s(f(ε)，f(x)度量了领域中心点x与邻近点ϵ像素的光度相似性；ω2为归一化参数。

2.1.3 双边滤波卷积

单独使用空间滤波无法全面考虑到像素点的位置影响，单独使用值域滤波也无法顾及像素点的差异影响。双边滤波是既考虑了像素点位置又考虑了像素点值的差异而提出的一种滤波方法。其卷积公式可表示如下:

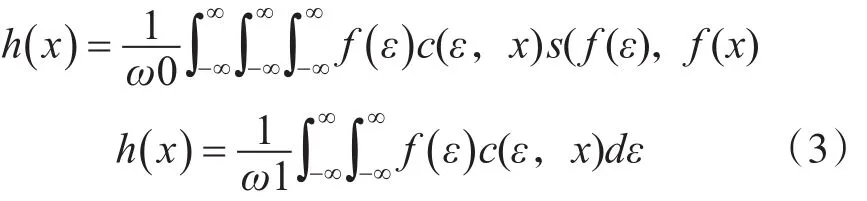
其中ω0=ω1ω2。

基于此思路，给出双边滤波的定义公式:

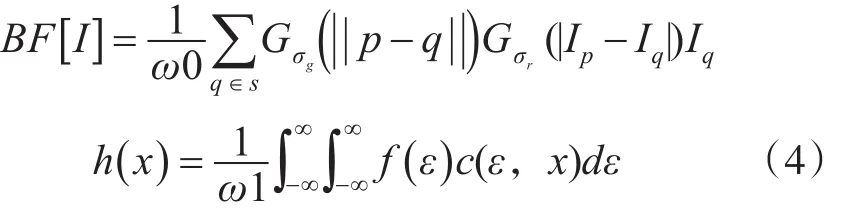
P代表邻近图像边缘信息的像素位置；q代表图像非边缘像素点的位置。Ip为p点的像素值；Iq为q点的像素值。∂g，∂r分别代表空间滤波器和值滤波器的标准方差，ω0表示为归一化因子。

在低频图像中，双边滤波器表现为空间滤波，原因在于低频图像邻近像素值差别较小，其像素位置对图像处理结果的影响大于像素值对图像的影响。反之，在高频图像中，双边滤波器表现为值域滤波，原因在于高频图像中图像的邻近像素值差别较大，对图像处理结果影响也较大［9～10］。

2.2 同态滤波

根据成像原理和光照特性，一副图像划分为照度分量i(x，y)和反射分量r(x，y），这样得到

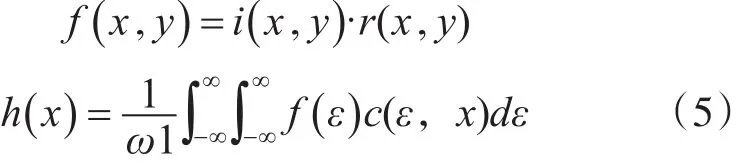
其中i(x，y)描述光照变化，图像中表现为低频区域；r(x，y）描述图像的细节信息，图像中表现为高频区域。

同态滤波的思路:首先将图像 f( )x，y 分解为描述光照变化的i(x，y)和描述图像细节的r(x，y）；其次对描述光照变化的i(x，y）进行合理压缩，同时对描述图像细节的 r(x，y）进行合理提升［7～8］。

将式（5）进行对数化处理，得

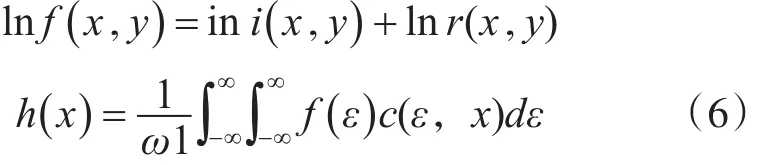
用离散余弦变换代替同态滤波的傅里叶变换对式（6）进行变换，得

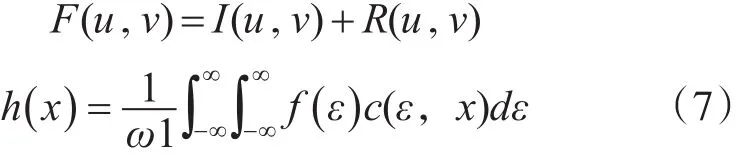
其中 F(u，v)=DCT(f(x，y))，I(u，v)=DCT(f(x，y)，R(u，v)=DCT(r(x，y))。

采用滤波函数对 H(u，v)对式（7）进行 F(u，v)进行处理，得

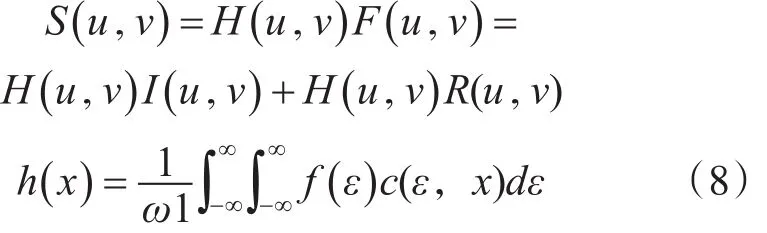
对滤波后的信号采用拟离散余弦变换可得

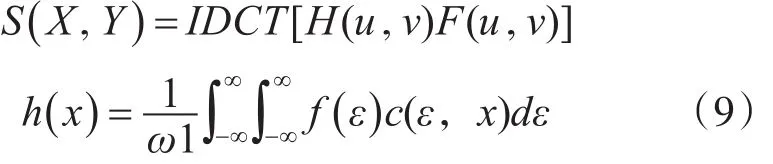
对上式进行指数变换，得出进行同态滤波后的输出图像为

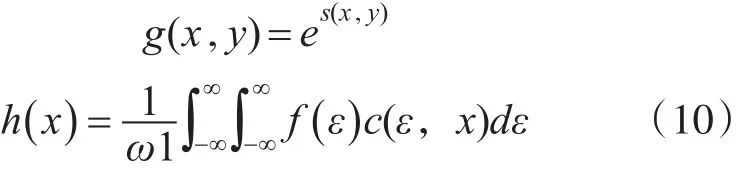
同态滤波后的图像质量与H(u，v)选择直接相关，为了消除光照变化的干扰，需要弱化i(u，v)，同时为了增强图像的细节，应该加大r(u，v)［11～13］。为此，对传统同态滤波器进行改进，具体如下:

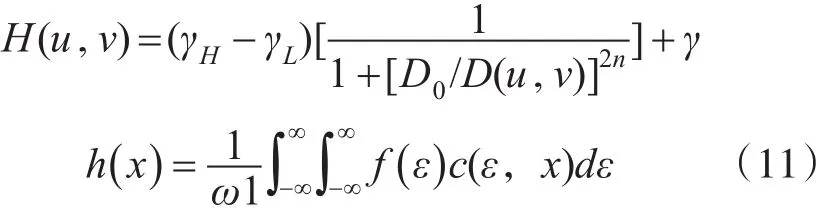
其中，n为阶数，D(u，v)为(u，v)与离散余弦变换频率原点的距离，具体计算公式:

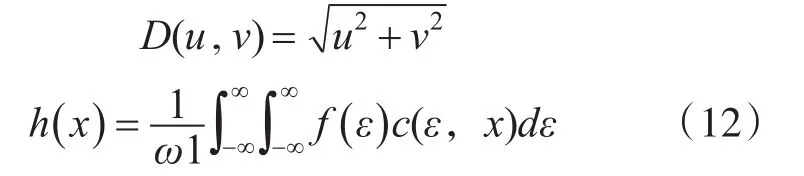
3 本文方法

3.1 流程图

图1所示为本文方法的流程图。X光机图像识别中图像双边滤波和同态滤波融合技术处理的过程如下。

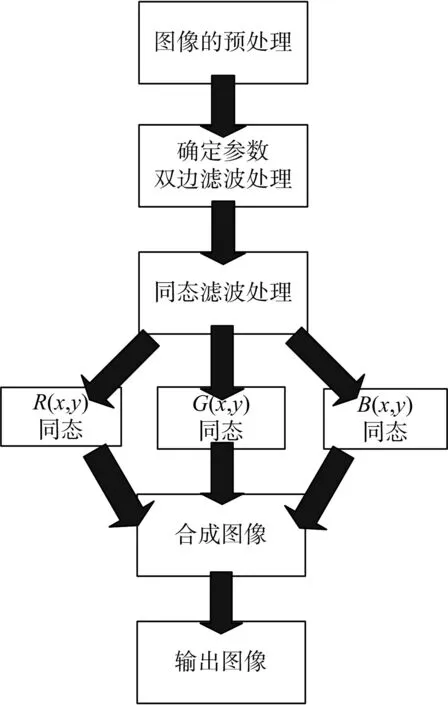
图1 本文方法的流程图

Step1:读入一幅待识别的图像，按照成像画面特点进行图像的预处理，得到预处理图像f(x，y)；

Step2:确定∂i∂r的值，对预处理图像进行双边滤波处理，得到双边滤波后的图像g(x，y)；

Step3:分离g(x，y)图像为R、G、B三通道的分通道图像，对分通道分别进行同态滤波处理，得到r(x，y)，g(x，y)，b(x，y)；

Step4:通过cat函数进行合成同态滤波后的三通道图像，得到u(x，y)；

Step5:输出u(x，y)图像。

3.2 ∂i∂r值的确定方法

在双边滤波中，随着σi变大，空间函数的作用变得突出，使图像去噪效果更加明显，但是值过大会导致图像纹理特征过于模糊；随着σr变大零度函数变得平滑而稳定其亮度突变的边缘基本保持恒定，使得双边滤波转化为高斯低通滤波，从而失去对边缘保持的约束作用。当∂i∂r值过小时，双边滤波的效果会消失。因此在本文中，依据经验选择几组参数进行处理，研究不同参数下的双边滤波效果，见表1。

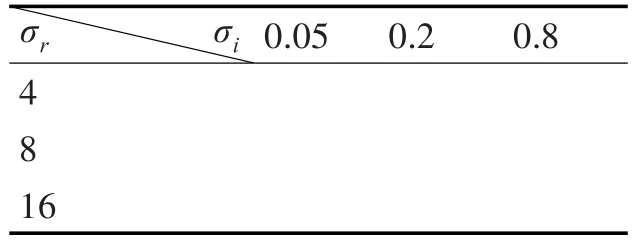
表1 双边滤波的不同参数

3.3 分通道的同态滤波方法

分通道的同态滤波方法是指将一幅图像进行转换到特定色彩模下，对此图像的各个色彩通道进行分离后同态处理，最后将同态处理的各个分通道图像进行合并，生成一幅特定色彩模式的图像。

图2所示为本文中图像的分通道的同态滤波方法流程图。具体的处理过程如下。

图2 分通道同态滤波处理流程图

Step1:读入一幅待处理图像，对待处理图像进行色彩空间转换f(x，y)→f(x，y)RGB，得到RGB色彩空间内的f(x，y)RGB。

Step2:利用Matlab将f(x，y)RGB图像进行分离在R、G、B三个颜色通道上，得f(x，y)R、f(x，y)G、f(x，y)B。

Step3:对 分 通 道图像f(x，y)R、f(x，y)G、f(x，y)B图像分别进行同态滤波处理，得到u(x，y)R、u(x，y)G、u(x，y)B。

Step4:利用Matlab软件将u(x，y)R、u(x，y)G、u(x，y)B进行合并，得到输出图像U(x，y)。

4 实验与讨论

4.1 实验数据

4.1.1 双边滤波数据

由于目前缺少能够用来测试σi、σr处理效果的X光机图像数据库，为了验证本文方法的有效性，利用X光机对一箱包进行扫描处理，得到如图3所示的原始图像。利用双边滤波算法对原始图像进行不同参数下的双边滤波处理，处理结果如表2所示。下面将对处理结果进行同态滤波处理。

图3 X光机原图

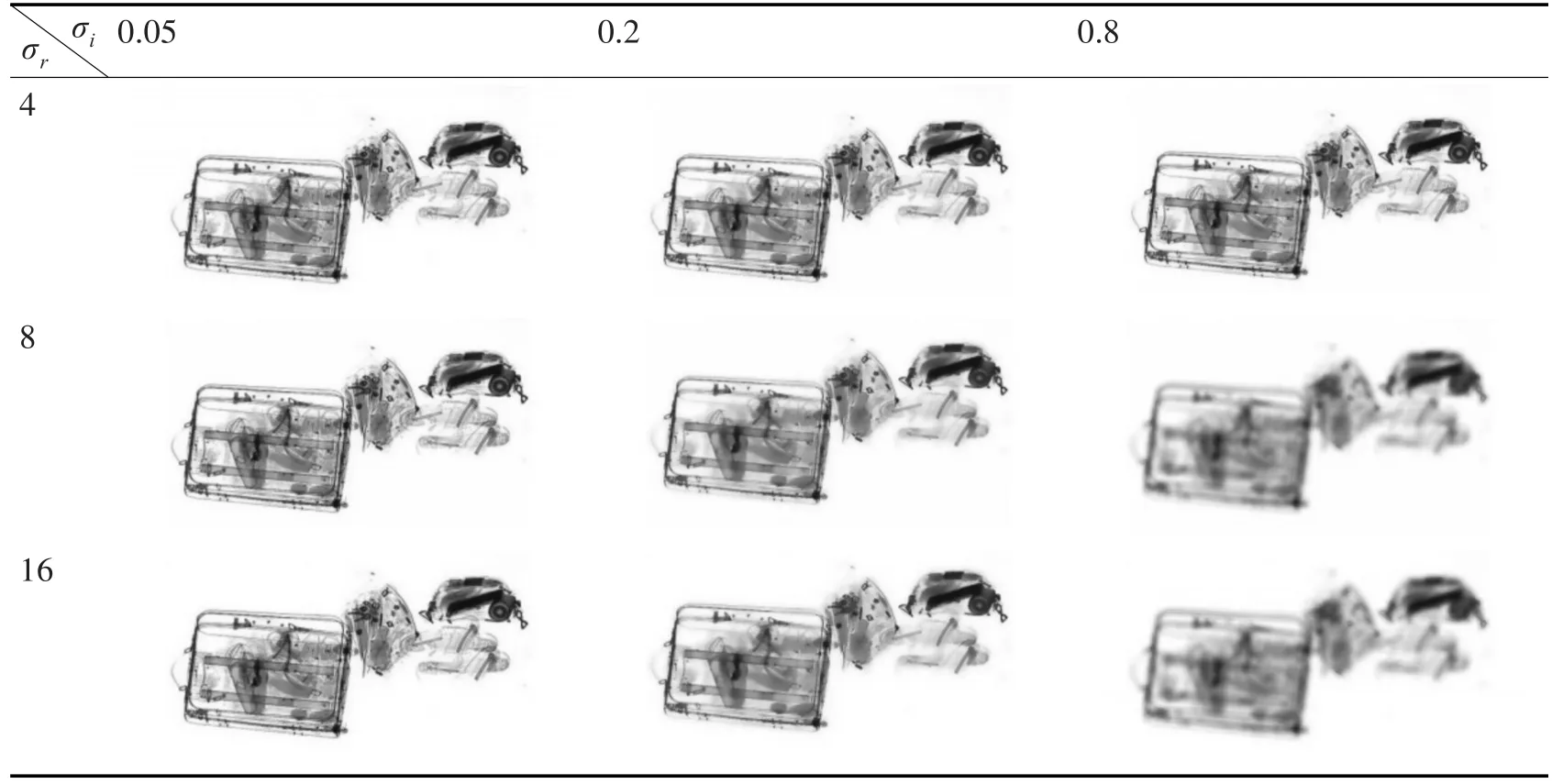
表2 不同σi、σr下双边滤波处理结果

4.1.2 同态滤波处理数据

从表2双边滤波的结果图中选择一张图像边缘信息呈现较为清晰的一张图像作为原图像进行同态滤波处理，处理结果如表3所示。

表3 不同参数下的同态滤波处理结果

4.2 实验结果

通过双边滤波与同态滤波相融合技术，对原始X光机图像进行处理，最终得到如表3所示的序列结果图。通过比对观察以及图像的高低频信息分布情况分析，发现一张边缘细节信息呈现最完整的结果图。通过比对表3序列结果图，得到当low=0.8，high=0.8时效果最好。处理结果见图4。

图4 处理结果图

4.3 处理结果的视觉分析

如表4所示为原始图像、双边滤波、本文方法处理结果比对图。在原始图像中，图像边缘信息较为模糊，对比度较低，识别困难；在双边滤波处理结果图中，图像边缘信息锐利，但对比度偏低，识别较为困难；在本文方法处理结果图中，图像的边缘信息锐利，且对比度较高，能够在安检过程中快速识别被检物体边缘信息。

4.4 处理结果的直方图分析

通过Matlab软件分别导出原始图像，双边滤波图像，本文方法图像的直方图（如表5所示）。

各个图像中像素值为255的像素数目从大到小依次本文方法结果图、双边滤波结果图、原始图像。根据像素在直方图中的分布规律，越趋近于正态分布，图像细节信息越丰富。因此，本文方法优于原始图像与双边滤波结果。

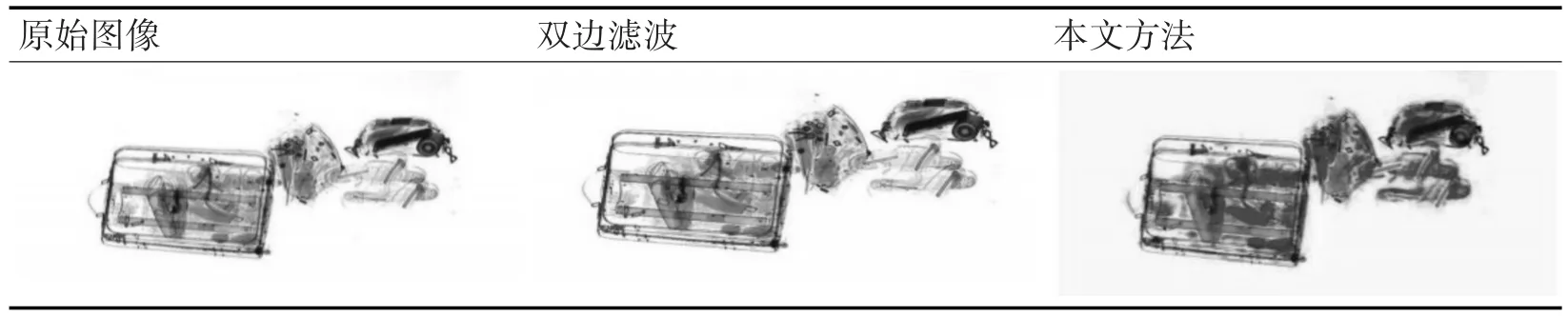
表4 处理结果比对图

表5 直方图比对结果

4.5 讨论

本文针对X光机图像运用双边滤波与同态滤波相融合技术进行图像处理，既可以解决图像的边缘锐化问题，同时也提高了图像的对比度。通过处理结果图在视觉和直方图两方面分析，均发现本文方法处理效果优于原始图像和双边滤波处理结果。因此本文的双边滤波和同态滤波相融合技术能够为安检过程中快速识别图像边缘信息提供技术支持。

需要指出的是本文方法通过机组相近参数进行双边滤波与同态滤波相融合技术处理，相邻组参数之间具有一定的误差，进而导致处理结果不一定是最优。但是只要所取参数之间相差不大，同时能够多取几组参数，同样可以达到优化原始X光机图像的目的。

5 结语

不同的滤波器处理方法都可以进行图像的锐化处理，但难以进行多方面均衡化考虑。本节从X光机成像特点以及双边滤波和同态滤波的优越性两个方面进行讨论本文方法在处理X光机图像中的优势。由于X光机图像成像是基于被成像物体的密度，因此很多情况下由于密度相近而导致图像边缘信息模糊，且X光机成像为了更加清晰准确地判断物品的细节信息；双边滤波是既考虑了像素点位置又考虑了像素点值的差异而提出的一种滤波方法；同态滤波能够提高图像的对比度，进而使得边缘信息更加清晰可视［14～16］。因此，在 X光机图像识别中采用双边滤波和同态滤波相融合技术能够更可靠地识别图像细节信息，进一步丰富了X光机图像的识别技术手段。