认知无线网络自适应信道选择与功率分配*
2019-05-31陈宾喆仇润鹤
陈宾喆 ,仇润鹤
(1.东华大学信息科学与技术学院,上海 201620;2.数字化纺织服装技术教育部工程研究中心,上海 201620)
0 引 言
随着通信网络的不断发展,人们对无线电设备和应用的需求日益增长,现在的5G网络对频谱的需求以及动态接入的要求越来越高,频谱稀缺[1]正成为一个严重的问题。因此,联邦通信委员会(Federal Communications Commission)和其他频谱监管机构考虑允许未经许可的认知次用户重用授权频谱,而不会对许可的授权主用户造成不可接受的干扰。同时,如何合理利用这仅限的频谱资源来满足用户不断提升的需求成为了日益严重的问题。在此背景下,多路径并行传输(Concurrent Multipath Transfer,CMT)[2],其定义为通过聚合各路径上的带宽资源,实现数据的快速传输,以提高对网络闲置资源的利用率。在认知无线电网络中,本文把多路径并行传输的方式运用在认知次用户传输上,这大大节约了稀缺的频谱资源,同时也提高了认知次用户的用户体验。
在认知无线电网络中,其关键实现问题之一包括动态和高效的频谱利用策略设计,其一,网络中结点必须不断感知频谱空闲后才能分配信道进行通信,其二,网络中的结点同时也必须对认知次用户发射功率进行限制才能确保结点对频谱授权主用户的功率干扰值在不影响其正常通信的门限范围值之内,从而有效保护授权主用户通信的服务质量。其三,为了能最大化利用频谱、节约频谱资源并且能使认知次用户完成通信,网络中的结点必须确保最小认知次用户服务质量的容量要求。因此有必要对认知无线电网络的信道分配和功率控制问题进行研究,从而有效地提升网络可靠性和整体性能。认知无线电技术可以使网络节点根据频谱的可用性和信道的状态信息机会地重新配置和调整其操作参数。现有的认知无线电网络频谱功率联合分配研究有AE Ewaisha等人提出了一种最优停止规划的自适应信道选择策略[3],该策略有效地提高了认知次用户吞吐量,王佳奇提出的基于认知网络系统模型的频谱功率联合分配算法[4],该算法采用了两步式的分配方法即先对信道进行分配再进行功率分配。Sharma D K等人提出了一种基于局部映射交叉(PMX)的信道分配遗传算法[5],该算法是一种处理干扰问题的鲁棒方法。Chabalala C S等人提出的基于混合式频谱接入方式的信道和功率分配算法[6],该算法运用了分支定界的思想确定所选择的信道。Youssef K等人提出了一种基于多用户正交频分复用(MU-OFDM)的认知无线电系统在不同衰落信道模型下的奇谱分配算法[7]以提高吞吐量。Yao K等人提出了一种定向图论模型来研究分布式信道和功率选择问题[8]。熊加毫提出一种基于离散的量子粒子群算法和Hooke Jeeves算法的多目标优化的信道分配机制[9],进而获得最优的信道分配方案。庄陵等人提出考虑频谱感知错误的CR资源分配算法,将资源分配分步简化为载波分配和功率分配,在干扰约束和功率约束条件下对次用户进行功率分配[10],该算法对主用户造成的干扰更小,CR系统可以获得更大的吞量。
本文在现有研究的基础上,提出了一种认知用户基于并行传输的自适应信道选择和功率分配策略,结合认知无线电网络背景,建立以总功率、最小信道认知次用户满意度容量要求和主次用户碰撞概率限制为约束条件,最大化次用户信道容量为目标函数的系统模型,并且应用拉格朗日凸优化与枚举算法对自适应信道选择与功率优化分配模型进行优化,验证了文章提出的自适应信道选择和功率分配策略有效地提高了网络的通信性能。
1 自适应信道选择与功率优化分配系统模型
在认知无线电网络中,认知次用户自适应选择信道进行并行数据传输,在不影响授权主用户正常通信的条件下分配功率。下文将先介绍系统的信道模型,然后将推导建立优化模型。
1.1 信道模型
在认知无线电网络中,为了确保主用户正常使用信道,认知次用户自适应选择空闲的信道资源进行并行传输,为此本文建立了图1所表示的信道模型,认知无线电网络中存在J,J≥K个信道,且其中有N={1,2,3…K}个空闲信道,K为空闲信道的基数,且自由信道信道增益向量为h={h1,h2,h3…hk},hi,∀i∈N为第i个信道的信道增益,认知次用户选择信道并行传输数据,且第i个信道选择状态向量为a={ai|ai∈ {0,1},∀i∈N},当第i个信道被选择时ai=1,反之ai=0,此外,第i个信道所对应的功率分配向量为p= {pi|pi≥0 ,∀i∈N}。
在无线通信中,香农信道容量定理描述了在噪声信道上以任意小的误差概率可靠地传输信息的最大速率,在量化数字通信系统设计的基本性能极限方面起着至关重要的作用。因此,功率和带宽是衡量通信系统信息容量限制的关键指标。在自适应信道选择和功率分配策略中,信道容量对功率分配和信道选择向量的关系并不复杂,根据香农定理,第i个信道的最大信息传输速率ri(ai,pi)为:

其中,B为带宽,σ2为高斯白噪声。为了后续计算的方便,令B=ln2,根据换底公式,对式(1)进行变换可得:

在自适应信道选择和功率分配策略中,认知次用户结点的信道容量取决于信道选择的数量,所以认知次用户总的信道容量Rk(a,p)为:
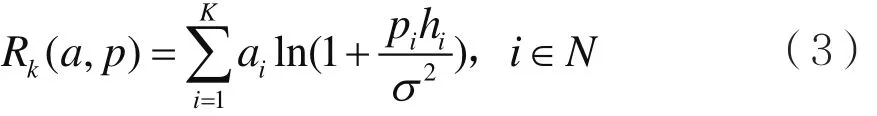
认知次用户可以自适应调整传输信道的数量,以及这些信道中的传输功率。但是,传输信道数量的增加了就会增加信道上授权主用户到达的概率,从而提高了认知次用户和授权主用户之间的碰撞概率,降低了两者的性能。

图1 信道模型
1.2 问题描述
本文主要考虑在认知无线网络的环境下,认知次用户自适应选择信道并行传输数据,为了不影响授权主用户的正常通信,对认知次用户进行功率分配以限制对授权主用户的干扰在可容忍的范围之内。模型目标是在满足碰撞概率限制、总功率限制和认知次用户最小通信满意度容量的要求下,最大化认知次用户的信道容量,其实质是混合0-1型整数非线性规划问题。
具体求解步骤如下:
(1)推导碰撞概率约束条件
根据现有的碰撞概率公式推导本文的碰撞概率限制不等式,并进行公式变形作为优化模型的约束条件。
(2)建立优化模型
根据本文的信道模型和并行传输的机制建立以次用户信道容量为目标函数,以碰撞概率限制,功率限制,最小次用户满意度容量限制和信道数限制为约束条件的优化模型,该模型实质为混合0-1型整数非线性规划问题。
(3)求解拉格朗日松弛解
对于混合0-1型整数非线性规划问题,首先,本文求解拉格朗日松弛解,为了进一步对所建模型进行优化,利用目标函数的特殊性质对模型进行变形,利用KKT条件和拉格朗日对偶函数将原问题转化为求拉格朗日对偶函数的最小值。本文把信道状态向量ai的元素放宽到闭区间[0,1]上,使用牛顿更新的方法进行信道状态向量的变换,并利用次梯度的思想对拉格朗日乘子进行更新,功率分配向量pi则是利用注水算法的思想与信道状态向量建立联系,最终得到最佳信道选择状态向量aioptrelx和最佳功率分配向量pioptrelx根据香浓定理求得信道容量松弛解。
(4)求解混合0-1整数非线性规划问题
本文利用信道枚举的思想将信道状态选择向量离散化到0和1,即信道选择状态向量利用枚举的方法进行更新,功率分配向量用注水算法,以拉格朗日求解所得到的信道容量松弛解为上界,0为下界寻求混合0-1整数非线性规划的原解,最终求得最佳信道选择状态向量aiopt与最佳功率分配向量piopt,根据香浓定理求解信道容量原解。
下文将首先介绍模型碰撞概率约束条件不等式的建立过程,其次建立优化模型并求解最佳次优解。
1.3 碰撞概率约束条件
假设授权主用户的到达率为λPU,在任一个信道上授权主用户的出现服从指数为λPU的泊松分布,那么在信道i上,τ时间内,认知次用户在授权主用户不出现的情况下完成传输的概率PrSUi为:
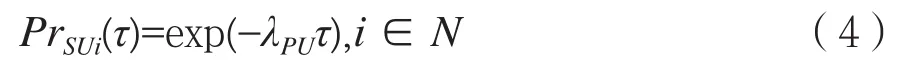
假设每个信道上的概率PrSUi是独立的,且所有被选择的信道Ch∈{1,2,…,Kch},其中Kch为所选信道。那么整个系统认知次用户在授权主用户不出现的情况下完成传输的概率PrSUCh(τ)为:

如果传输数据的长度为LSU,那么传输数据所用的时间TSU为:

由此,可以得到在TSU时间内整个系统认知次用户在授权主用户不出现的情况下完成传输的概率PrSUCh(TSU)为:

由式(7)可以看出认知次用户所分配的功率越大,系统认知次用户在授权主用户不出现的情况下完成传输的概率就越大,那么系统碰撞概率就越小。为了确保授权主用户的正常通信,必须设置碰撞概率门限Prω,使得Prω≤PrSUCh(TSU)即:
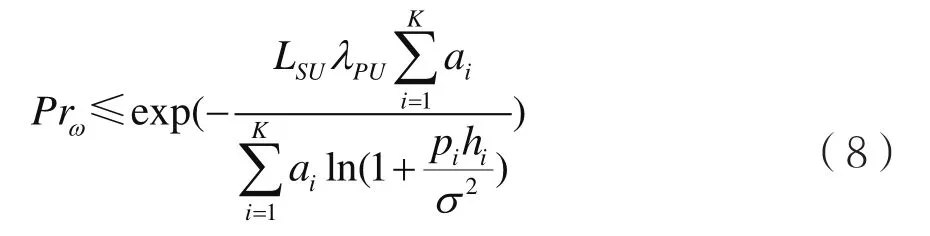
式(8)经过简单的公式变形,就可以得到式(9):

其中:

由此,碰撞概率的约束条件式已经推得。下文将介绍优化模型。
1.4 优化模型
结合信道模型和上节推得碰撞概率约束条件,联系总功率限制条件和认知次用户最小通信满意度容量的限制,认知无线电网络信道自适应选择和功率分配数学优化模型P1如下:

以及上述已推得的碰撞概率约束条件式(9)。
其中,Pmax表示认知次用户最大传输功率,RminSU则表示认知次用户最小信道满意度容量要求。式(12)表示认知次用户功率不能超过门限,从而影响主用户的正常通信。式(13)表示次用户的认知次用户最小信道服务质量容量要求,确保次用户的最低通信要求。式(9)表示认知次用户与授权主用户之间的碰撞概率限制。式(14)则表示信道选择状态,即认知次用户使用的信道数不能超过总的信道数。本节建立了优化模型,下节将求取模型的松弛解。
2 模型求解
对所建立的优化模型先进行等价变换,针对变换后的模型构造拉格朗日函数并求解松弛解,然后以求得的松弛解作为限制条件,结合信道枚举的方法求解原混合0-1型整数非线性规划的原解。接下来本文将介绍模型的求解过程。
2.1 拉格朗日求解松弛解
针对1.4节建立的优化模型,为了能得到更好的优化结果,考虑到ai∈{0,1}的特殊性,当ai=0时,当ai=1时,根据这一特性做如下推导:
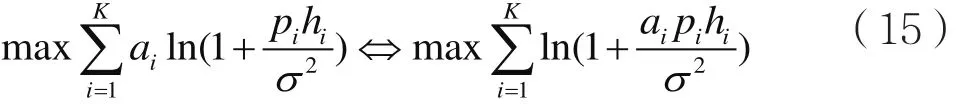
根据上述推导,将优化问题P1转化为优化问题P2:
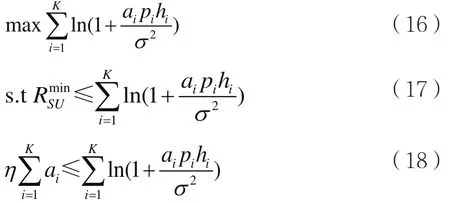
以及功率约束条件式(12)、信道状态约束条件式(14)。
根据文献[4]中的证明,目标函数是关于ai和pi的凸函数。对模型使用拉格朗日法重构法并结合KKT(Karush-Kuhn-Tucher)条件,将混合0-1型整数非线性规划问题转化为凸优化问题[11]。其次,对信道选择变量进行松弛化处理,即把变量ai的取值放宽到区间[0,1],求得的松弛解为原最优解提供上界,然后通过枚举法求得原最优解。构造后的拉格朗日函数F(a,p,λ)为:

其中 ,λ={λm≥ 0,m=1,2,3},对偶问题的求解相对容易,从对偶问题的解中可以分析得到原问题的解,根据文献[12],对构造的拉格朗日函数进行对偶分解,原庞大的优化问题可以转化为针对每个信道的多个子问题,并把原问题转化为求拉格朗日函数的最小值,各个子问题的拉格朗日函数为:
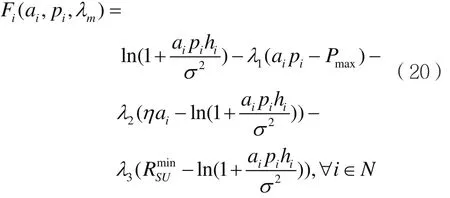
接着根据KKT条件和文献[8],通过牛顿迭代法对ai进行迭代更新即:
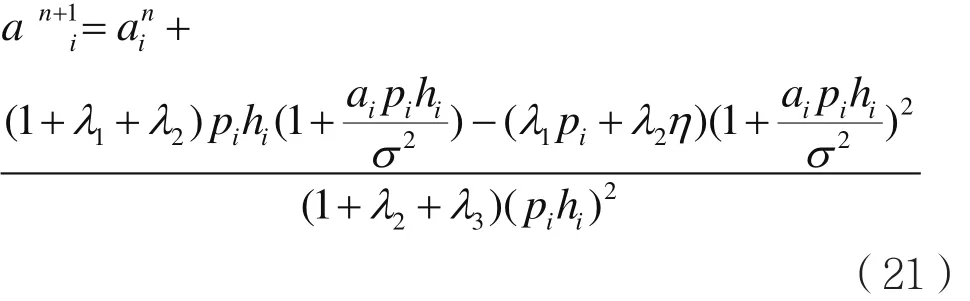
其中,对拉格朗日乘子λ通过次梯度迭代方式的更新式为:
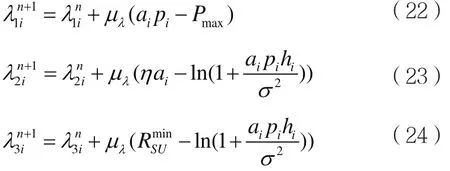
其中,μλ为更新步长。对于功率分配方面,本文采用注水定理[13]进行功率分配即:
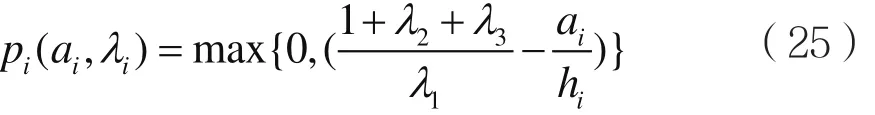
很明显,功率分配的大小取决于信道增益的大小,对于信道增益大的信道分配的功率比信道增益小的功率要大。
本节介绍了对变形后的优化模型构造拉格朗日函数,利用对偶分解理论对拉格朗日函数进行简化,并且求解拉格朗日最优解得到优化模型的松弛解。下节将利用枚举的方法结合松弛解的限制求得优化模型的原解。
2.2 枚举法求解原解
本节的主要目标是从松弛最优解中恢复原始最优解。在求的松弛解为上限条件下,本文简单地以0为下限,把枚举法[14-15]引入信道选择上,通过对松弛变量的系统枚举,提出了一种信道选择向量离散性的算法。这种枚举的算法特点是计算结果比较精确,但是对于多信道的场景下算法复杂度较高且计算时间较长。对于本文实质优化问题混合0-1整数非线性规划问题来说,凸优化和枚举思想的结合是一种比较精确可靠的方法,在信道数目不大的情况下,能有效地得到最佳次优解,但对于数目较大的信道情况下,这种算法求解模型比较慢。
图2即为信道枚举法求原最优解的算法流程。首先列举信道选择向量的选择情况,根据信道选择情况对功率分配向量进行更新,结合信道选择向量和功率分配向量来求目标函数,在目标函数满足功率限制、最低传输速率限制、碰撞概率限制和松弛解限制的条件,即是最佳次优解向量。对于本文混合0-1型非线性整数规划问题,利用拉格朗日函数求得松弛解,再利用枚举法的原理将信道选择状态向量ai在闭区间[0,1]离散化到0和1,从而求得满足条件限制的最大目标函数。
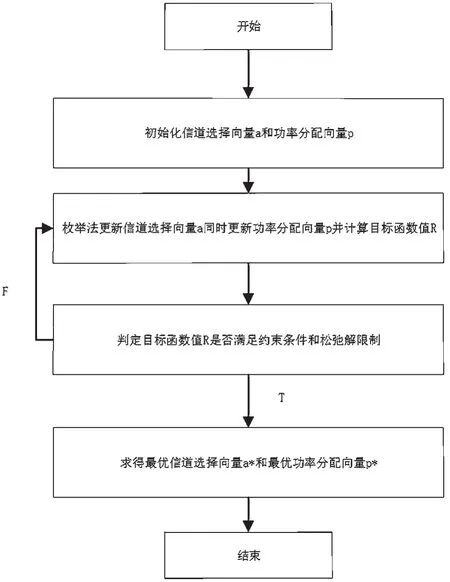
图2 信道枚举法算法流程
凸优化和枚举法的结合比直接用枚举法求解效率更高,而且更接近最优解,能更直接地得到最优信道选择向量和最优功率分配向量,使得优化模型的解更加精确。
3 仿真分析
3.1 模型参数设置
表1所示为本文模型参数设置,在认知无线电的背景下,授权主用户的出现服从泊松分布,且每个信道之间互相独立,认知次用户根据信道增益自适应选择空闲信道并行传输数据,结果主要分析主次用户之间碰撞概率限制在0.1、0.2和0.3情况时的信道容量和碰撞概率。
本文引入现有的遗传算法[16]作为检验标准,其原理即同时将信道选择状态向量ai,功率分配向量pi作为染色体进行更新,从而求得满足条件的最大信道容量值,参数设置为种群数1 000,遗传代数100。
3.2 算法复杂度和收敛性
3.2.1 算法复杂度
本文算法的拉格朗日对偶分解优化部分有2×N个变量,所以其算法复杂度为O(2N),该项与后面信道枚举法求原解调整时间O(N)相加,应为O(3N)。表2所示为本文算法和遗传算法的算法复杂度对比,很明显可以看出,本文算法所用时间15.6 s而遗传算法所用的时间为本文算法的3倍左右,所以在算法复杂度上,本文算法比较效率较高。

表2 算法复杂度
3.2.2 收敛性
图3为本文对偶分解部分拉格朗日函数值与迭代次数的变化关系,当迭代到20次时,拉格朗日函数值趋于稳定,收敛于8.584 7。

图3 本文算法收敛性
3.3 仿真结果
3.3.1 碰撞概率限制0.3时的仿真结果
图4是在碰撞概率限制为0.3时候的信道容量,图4中十字点线代表的是所求得松弛解即上界,倒三角点线是最终求得的原解,星点线是遗传算法下的信道容量,圆点线是下界,很明显可以看出,随着授权主用户到达率的增加,信道容量是呈递减的态势,但是由于两种算法在信道选择和功率分配上的差异性使得两曲线在信道容量曲线有所不同,可以看出,在主用户到达率较小时原解接近松弛解,主用户到达率在0~0.66区间内信道容量比遗传算法效果更佳,到达率0.67~1区间内两种算法本文算法不做信道选择,所以信道容量为0,而遗传算法的曲线在到达率大于0.9时不做信道选择。

图4 碰撞概率限制0.3时的信道容量
图5 是碰撞概率限制为0.3时的碰撞概率曲线。
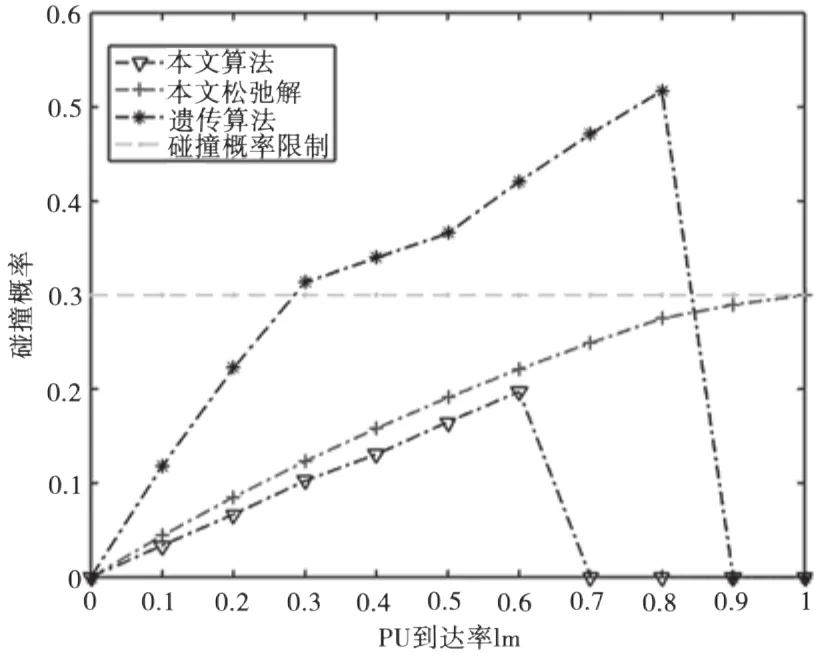
图5 碰撞概率限制0.3时的碰撞概率
图5 中,从上至下,其中星点线为遗传算法下的碰撞概率曲线,虚线为碰撞概率的界限,十字点线为本文松弛解的碰撞概率曲线,倒三角点线为本文算法的曲线。很明显,随着主用户到达率的上升,碰撞概率随之上升。本文算法所求得的松弛解和原解都能在碰撞概率限制之下,然而遗传算法下的碰撞概率在主用户到达率为0.29~0.85时,概率超出了碰撞概率的界限,大于0.9时不做信道选择,所以碰撞概率为0。本文算法仿真结果比遗传算法下的碰撞概率小,对授权主用户的使用影响小。当授权主用户到达率大于0.7时,由于信道不被选择,碰撞概率为0。
3.3.2 碰撞概率限制0.2时的仿真结果
图6是在碰撞概率限制为0.2时候的信道容量,图6中十字点线代表的是本文松弛解的曲线即上界,倒三角点线是本文算法求得的曲线,星点线是遗传算法下的信道容量,圆点线是下界,很明显可以看出,随着授权主用户到达率的增加,信道容量是呈递减的趋势,在主用户到达率较小时原解接近松弛解,且在本文的算法下,信道容量比遗传算法的信道容量高,当主用户的到达率大于0.6时不做选择信道,所以信道容量为0。
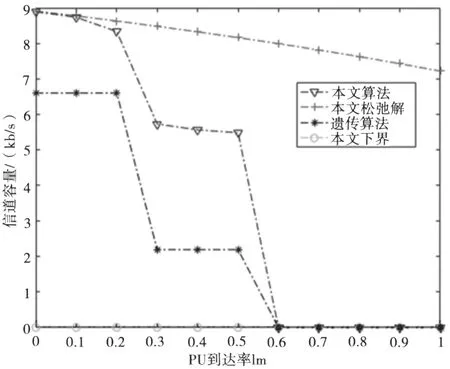
图6 碰撞概率限制0.2时的信道容量
图7 是碰撞概率限制为0.2时的碰撞概率曲线。

图7 碰撞概率限制0.2时的碰撞概率曲线
图7中,从上至下,其中星点线为遗传算法的碰撞概率曲线,虚线为碰撞概率的界限,十字点线本文松弛解的碰撞概率曲线,倒三角点线为原解所求得的曲线。很明显,本文算法所求得的松弛解和原解都能在碰撞概率限制之下,然而遗传算法下的碰撞概率在授权主用户的到达率在0.49~0.51的区间内,其概率超出了碰撞概率的界限,本文所提算法仿真结果比遗传算法下的曲线效果好,当授权主用户到达率大于0.6时,由于信道不被选择,碰撞概率为0。
3.3.3 碰撞概率限制0.1时的仿真结果
图8是在碰撞概率限制为0.1时候的信道容量,图8中十字点线代表的是本文松弛解曲线即上界,倒三角点线是最终求得的原解,星点线是遗传算法下的信道容量,圆点线是下界,很明显可以看出,随着授权主用户到达率的增加,信道容量是呈递减的态势,在本文的算法下,信道容量比遗传算法下的信道容量高,当主用户的到达率大于0.5时不选择信道,所以信道容量为0。在遗传算法下,当主用户抵达率大于0.3时不做信道选择,信道容量为0。
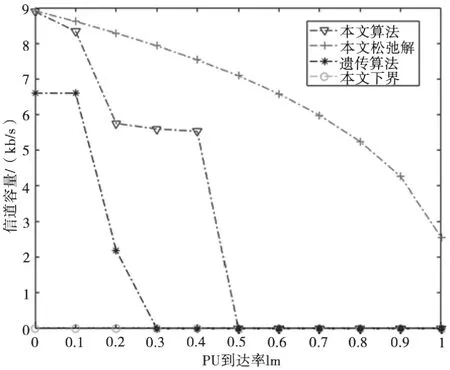
图8 碰撞概率限制0.1时的信道容量
图9 是碰撞概率限制为0.1时的碰撞概率曲线,从上至下,其中星点线为遗传算法下的碰撞概率曲线,虚线为碰撞概率的界限,十字点线为本文松弛解的碰撞概率曲线,倒三角点线为原解所求得的曲线。很明显,本文算法所求得的松弛解和原解都能在碰撞概率限制之下,而且,遗传算法下的碰撞概率曲线在授权主用户的到达率在0.06~0.26时,碰撞概率超出了界限,本文所提算法仿真结果比遗传算法下的碰撞概率曲线效果更优,当授权主用户到达率大于0.5时,由于信道不被选择,不会存在碰撞概率,即碰撞概率为0。在遗传算法下,当主用户抵达率大于0.3时不做信道选择,碰撞概率为0。

图9 碰撞概率限制0.1时的碰撞概率
4 结语和展望
仿真结果表明,本文的算法在信道容量和碰撞概率两个性能指标上优于遗传算法下的分配策略,且授权主用户的到达率是信道选择和功率分配的关键因素。随着碰撞概率限制条件越发苛刻,信道被选择的机会越来越少,因此,在信道容量和碰撞概率的性能上表现得越差,除此,在信道容量和碰撞概率上两个和性能上,本文信道容量松弛解曲线一直不为0,其原因是在求解松弛解的情况下,信道选择向量一直保持在[0,1],使得功率分配向量也不为0。综上所述,在认知无线电网络授权次用户并行传输的场景下,本文自适应信道选择和功率分配的策略在信道容量和碰撞概率上均有较好的性能发挥。
本文建立了以碰撞概率为主要限制条件的自适应信道选择与功率分配的认知无线电网络模型,利用拉格朗日凸优化和信道枚举法相结合的方法求解该模型。在认知无线电网络中,确保用户通信正常的限制条件有很多,下一步将替换碰撞概率的限制条件,考虑一些限制条件,比如干扰温度、主用户的满意度等等,对模型进行改变,并结合一些现有的算法对模型进行求解。
