利用遗传BP神经网络的调制识别新算法*

吴喜权，高 勇

（四川大学 电子信息学院，四川 成都 610065）

0 引 言

在通信技术高速发展的今天，无论是在军事还是民用领域，通信信号的调制识别都一直是人们关注的焦点。对信号调制方式的准确识别是对信号正确解调、获取通信信息的重要保证。因此对通信信号调制识别的研究具有十分重要的意义。

许多学者对通信信号调制方式的自动识别进行了大量的研究，其主要是基于星座图重构[1-2］、压缩感知理论与信号的非线性变换相结合[3-5］、相位编码统计[6］、循环累计量[7］、二次方谱相关特征[8］、高阶累积量[9］、小波变换[10］等方法提取信号特征以识别信号，对通信信号调制方式自动识别的发展做出了重要贡献。但是这些方法也有进一步改进之处。比如，重构星座图的减法聚类算法对不同调制阶数信号要求的聚类半径不同且难以预先确定。聚类半径较大对高阶调制信号的星座图重构效果较差，较小则对低阶调制信号星座图重构效果较差；基于信号N次方非线性变换以及压缩感知理论提取特征对信号进行识别，运算复杂度较高；采用相位编码统计方法识别信号，虽然算法具有良好的抗频偏性能，但是在实际应用中该算法相位差分的阶数依赖于待识别信号的信噪比且阶数越大运算量和工程实现的复杂度就会越大；利用信号循环累积量的特征对信号进行识别，需要信号载频这一先验信息且循环累积量运算量也较大；而基于信号的二次方谱相关特征识别信号，虽然不受信号幅度变化的影响且运算复杂度相对信号循环累积量的运算复杂度较低，但该算法也依赖于信号载频这一先验信息；此外只依赖于信号高阶累计量的方法，在相同信号类型间识别时也不能有效区分信号。传统的通信信号调制方式自动识别方法大多都采用二叉树分类器结合信号特征区分信号，一般都会设定一个固定门限值。但是在低信噪比下采用传统二叉树分类器单靠设置固定门限去区分信号其效果不理想，且在低信噪比下判决门限也不易选取，门限设定恰当与否直接影响识别的性能。

为此，利用信号高阶累积量、瞬时幅度谱以及信号N次方非线性变换后的特征提取新的参数并采用遗传算法优化的BP神经网络作为分类器识别信号。实验结果表明在低信噪比下对2FSK、BPSK、QPSK、UQPSK、8PSK等5种通信中常用信号能有效识别。

1 特征提取

1.1 信号瞬时幅度谱

接收端含噪声的数字调制信号经下变频后可表示为[9］:

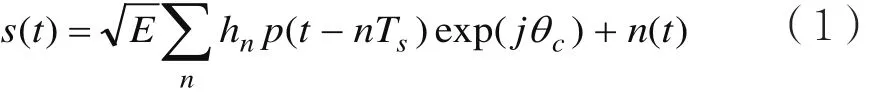
式中，p(t)是发送码元波形，Ts为码元宽度，θc为载波相位，hn为发送码元序列，E为发送码元波形的能量。n(t)为零均值的复高斯白噪声。

定义信号的瞬时幅度谱为：

式中，I、Q为信号的同相和正交分量，FT(•)表示傅里叶变换。如图1所示，BPSK、QPSK、UQPSK以及8PSK信号经过幅度归一化后的瞬时幅度谱在±500 kHz（码速率）处各具有一个很强的冲激。而FSK信号则没有，其经过幅度归一化后的瞬时幅度谱如图2所示。本文根据这两个冲激之间的宽度提取特征参数T1以区分2FSK信号与BPSK、QPSK、UQPSK、8PSK信号。

图1 PSK信号经幅度归一化后的瞬时幅度谱

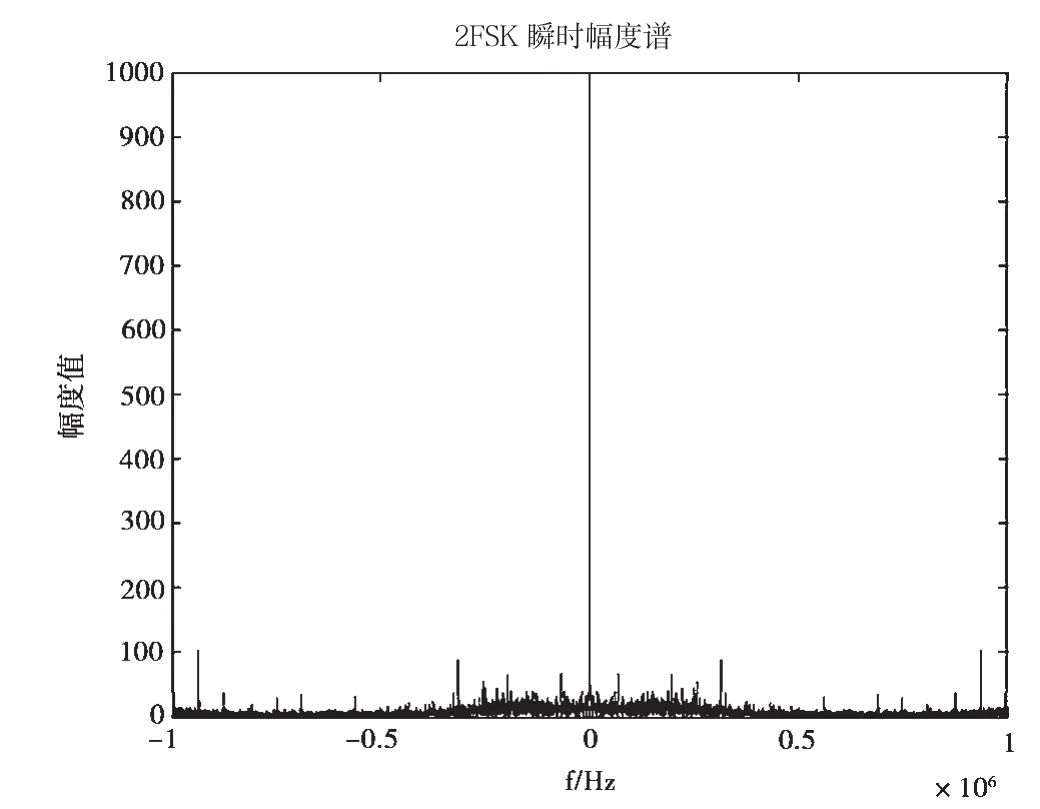
图2 2FSK信号经幅度归一化后的瞬时幅度谱

1.2 基于信号高阶累积量的非线性变换

信号的调制特点不仅反映在信号幅度谱，也反映在信号时域高阶累积量上，且信号大于二阶的高阶累积量可以抑制高斯噪声的影响[9］。

设复随机过程s(k)的均值为零，其p阶混合矩定义为[9,11］：

其中，s*(k)表示s(k)的共轭，E[•］表示期望。

则s(k)的高阶累积量定义为[11］：

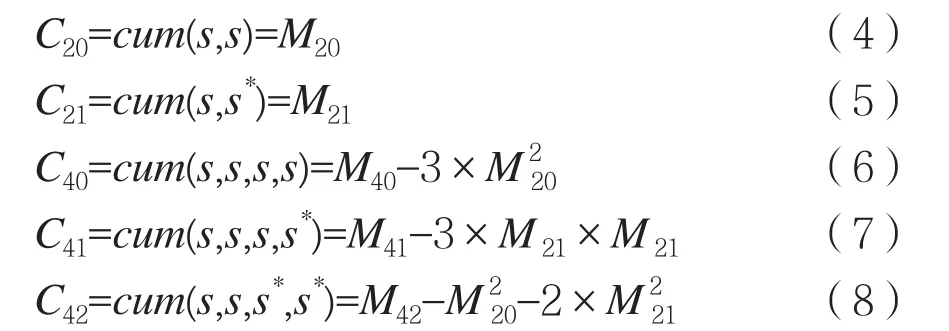
信号四阶累积量的理论值如表1所示[11-12］，其中E表示信号能量。

表1 信号四阶累积量理论值

在数字信号自动调制识别领域尤其是对MPSK信号的调制识别，信号N次方非线性变换是一种常用的方法[5］。本文根据信号高阶累积量以及信号N次方非线性变换[5］提取特征参数：

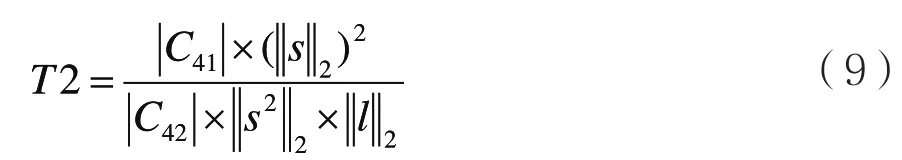
式中，s表示信号，l表示1行n列且元素全为1的向量，n为信号长度，||•||2表示2范数。

以BPSK信号为例对上述特征参数进行理论推导，初相为0的BPSK信号归一化后的星座图只有两个点，（1,0）和（-1,0）且各自占1/2的概率[5］。则BPSK信号T2、T2的理论值计算如下：

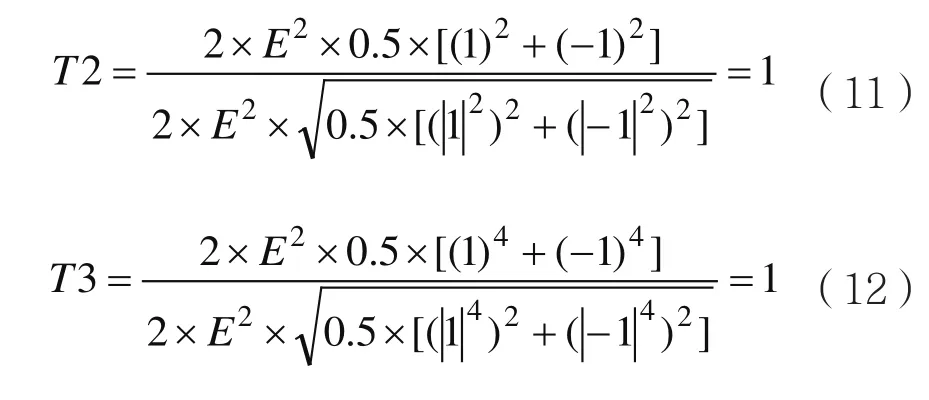
各信号特征参数的理论值如表2所示。其中UQPSK信号的非平衡因子[12］选取为0.3。

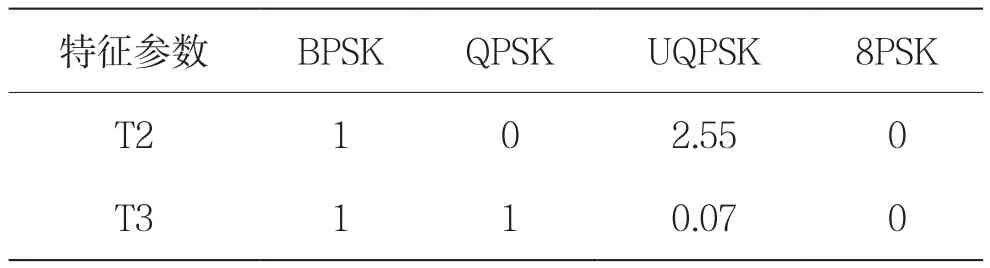
表2 信号特征参数的理论值

2 分类器设计

本文采用经过Sheffield遗传算法优化的BP神经网络作为调制识别分类器。BP神经网络的初始连接权值和阈值对网络训练的影响很大，但又无法准确获得。在使用BP神经网络时，一般是通过初始化为[-0.5,0.5］区间的随机数作为网络的初始权值和阈值[13-14］。经实验证明这种情况下网络对于相同的样本其输出结果不稳定，因此可以用遗传算法优化BP网络的初始权值和阈值,使网络能更好地进行样本预测。

本文BP神经网络采用三层网络结构，包括输入层、隐含层、输出层[14-16］，其结构如图3所示。网络的输入采用列向量输入，即[T1T2T3］T。输出采用列向量输出，总共有5种输出，每次输出都是式（13）的一列。第一列代表2FSK信号，第二列代表BPSK信号，以此类推。实际输出向量的每个元素都在0到1之间，判别信号时在每列中选出最大值置为1，其余元素置为0。

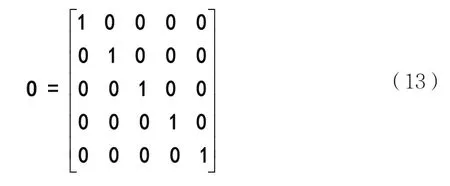
设输入层神经元个数为n1，隐含层节点数目n2和n1之间有近似关系：

本文对信号提取三个特征参数，因此n1=3，n2=7。网络输出层节点数为5，分别对应五种待识别信号。网络共有3×7+7×5=56个权值，7+5=12个阈值。所以遗传算法优化的参数个数为68个，包含56个权值和12个阈值。

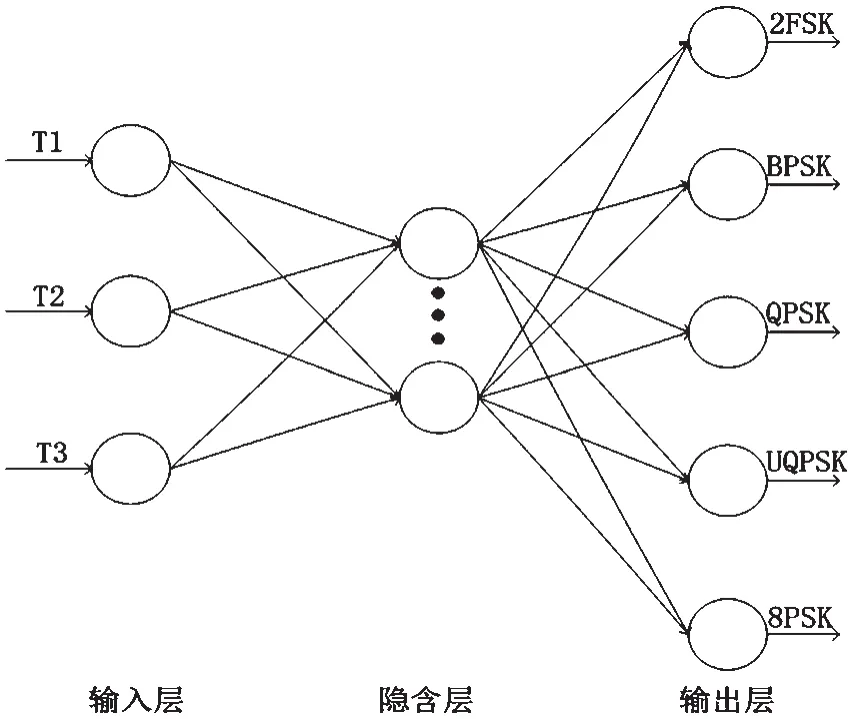
图3 三层BP神经网络结构

3 信号识别流程

信号识别算法流程如下：

（1）对信号进行幅度归一化、中值滤波。

（2）提取特征T1、T2、T3，特征样本采集。

（3）遗传算法优化神经网络。

（4）神经网络识别信号。

信号识别流程如图4所示。

4 仿真与结果分析

每个仿真信号长度为7 000个样点，码速率为400～600 KBaud，采样率为4倍码速率。每种信号在-3～16 dB共生成1 000个特征样本来训练BP神经网络，然后每种信号再在-3～16 dB生成1 000个特征样本进行测试。信号识别率如图5所示。

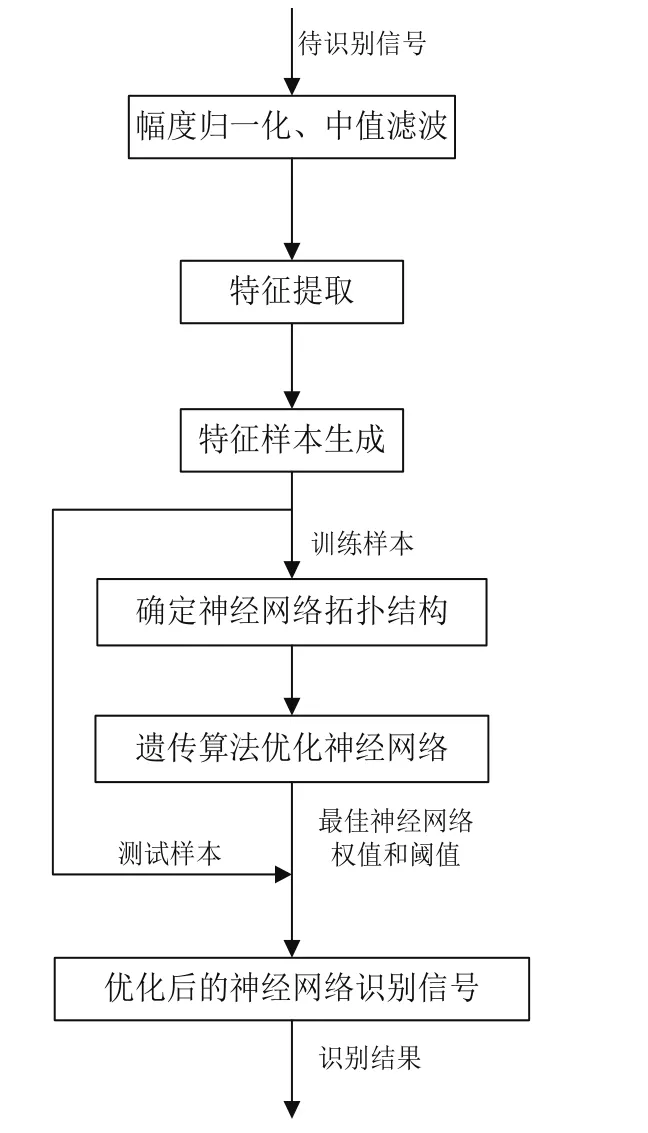
图4 信号识别流程

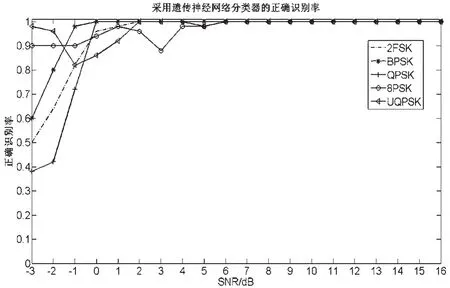
图5 采用遗传神经网络分类器的信号识别率

可见采用本文的方法在低信噪比下对信号具有良好的识别效果。其中对于BPSK、QPSK信号在0 dB时识别率可达96%以上，其余信号在信噪比大于0 dB时信号识别率均能达到85%以上。

在与本文相同的实验条件下，若采用传统二叉树分类器进行信号的识别，其识别率如图6所示。

由图6可以看出，采用传统二叉树分类器单靠设置的固定门限去区分信号在低信噪比下识别效果不理想。这是因为在低信噪比下，提取的信号特征往往区分不明显，而本文采用的经遗传算法优化的BP神经网络分类器不需要设置固定门限，很好的改善了这一问题，其与采用传统二叉树分类器的平均识别率的对比如图7所示。

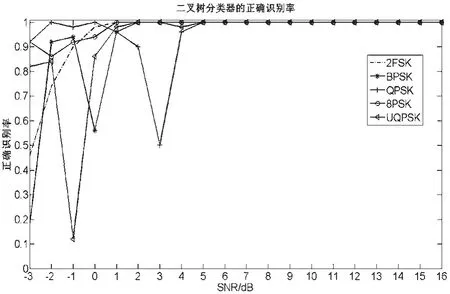
图6 采用二叉树分类器的信号识别率

图7 平均识别率对比

通过图7可见在本文实验中采用遗传算法优化的神经网络分类器比二叉树分类器在低信噪比下识别效果更稳定，且在信噪比大于0 dB时平均识别率更高。

5 结 语

为了在低信噪比下有效识别通信信号，提出一种利用遗传BP神经网络的信号调制识别新算法。理论分析与实验结果表明，该算法在低信噪比下对2FSK、BPSK、QPSK、UQPSK、8PSK五种通信中常用的调制信号具有良好的识别效果。且在相同的实验条件下，采用遗传算法优化的神经网络分类器与二叉树分类器相比在低信噪比下效果更稳定，当信噪比大于0 dB时平均识别率更高。此外，本文提取的特征相较于基于星座图重构、信号循环谱、压缩感知理论等提取的特征更易于计算。值得提出的是，采用遗传算法优化的神经网络分类器要获得较好的性能需要大量的训练样本，且训练时间较长，但一旦训练完成，用于识别信号的速度能达到实时处理信号的要求。后续可通过深度神经网络进一步改善识别性能。